2. 广西可信软件重点实验室 (桂林电子科技大学), 广西 桂林 541004;
3. 贵州省黔南师范学院 数学与统计学院, 贵州 都匀 558000
2. Guangxi Key Laboratory of Trusted Software (Guilin University of Electronic Technology), Guilin 541004, China;
3. School of Mathematics and Statistics, Qiannan Normal College for Nationalities, Duyun 558000, China
离散事件系统诊断是一种基于模型诊断 (model-based diagnosis, 简称MBD) 的动态方法[1, 2].通常采用有限状态自动机 (finite state machine, 简称FSM) 对离散事件系统 (discrete-event system, 简称DES)[3]进行建模, 结合实际观测, 推理得到系统的诊断结果.通过诊断, 可以判断实际系统运行是否正常; 若有故障发生, 则定位故障和确定故障类型, 从而有助于及时排除故障, 保障系统的正常运行.文献[4, 5]分别对MBD和离散事件系统诊断的研究现状和进展进行了系统阐述.
离散事件系统诊断通常基于两个假定前提:系统模型的完备性和可诊断性, 保证系统得到诊断结果的唯一性和正确性[6].系统模型的完备性前提是指:系统全部可能的行为均被包含在系统模型中.对于一些复杂的实际系统, 建立完备的模型往往非常困难, 因此, 一些学者对系统不完备情况下的诊断展开了研究[6-9].
离散事件系统的可诊断性前提是指:在获得足够多的观测后, 任意故障的发生均能够被唯一地判定.文献[1, 10]分别从不同角度给出了离散事件系统可诊断性的定义.文献[10]从状态识别 (state identification) 的角度来讨论可诊断性, 分别定义了离线 (off-line) 可诊断性和在线 (on-line) 可诊断性, 并给出了判定方法.文献[1]从事件发觉 (event detection) 的角度来讨论可诊断性, 分别定义了可诊断性和I-可诊断性, 并给出了判定方法.在文献[1]中, 依据系统模型构建诊断器 (diagnoser), 该诊断器一方面完成诊断的任务, 另一方面也用于判定可诊断性.其判定算法的时间复杂度是系统状态数的指数倍和故障类型数的双重指数倍.文献[11]对文献[1]中方法进行了改进, 通过构造预诊断器, 然后利用预诊断器的同步来判断可诊断性, 该方法通常被称为双树 (twin-plant) 方法, 其将可诊断性判定的效率由指数级降为多项式级, 即系统状态数的四次方.
对于离散事件系统诊断和可诊断性的研究, 出于简单性考虑, 大都假定系统观测是确定的.即系统发生一系列行为后, 在线观测系统能够准确获取可观测事件的信息, 包括什么事件发生了以及这些事件发生的先后次序.但在实际应用中, 由于信息传输以及感知器的精度等原因, 往往很难获取到确定的观测信息, 这给系统诊断和可诊断性判定带来了困难.因此, 一些学者展开了不确定观测条件下离散事件系统诊断和可诊断性的研究.在文献[12]中, Lamperti等人将观测不确定分为4类:时序不确定、丢失不确定、逻辑不确定和来源不确定, 并提出各类观测不确定条件下的诊断方法, 但并未对其可诊断性展开研究.Grastien等人在文献[13, 14]中分别考虑了观测部分有序 (即时序不确定) 离散事件系统的可诊断性和诊断问题.Su等人在文献[15]中给出了时序不确定和逻辑不确定条件下离散事件系统可诊断性的判定方法.
本文重点对观测不确定条件下离散事件系统的可诊断性问题展开研究.可诊断性是诊断系统一个非常重要的性质, 其保障诊断结果的正确性和唯一性.离散事件系统的诊断依赖于对实际系统的建模和实际观测, 而实际观测的不确定会严重影响系统的可诊断性.通过采用更精密的感知器或更可靠的信息传输通道, 在一定程度上可以消除一部分观测不确定, 但这样花费的成本往往非常高.因此, 对观测不确定条件下的可诊断性研究具有现实意义.
本文第1节给出离散事件系统诊断和可诊断性的相关概念和定义以及可诊断性的判定方法.第2节介绍各类观测不确定, 并创新形式化其对实际观测的影响.第3节扩展传统可诊断性的定义, 给出观测不确定条件下的可诊断性定义, 并分别给出各类观测不确定条件下的可诊断性判定方法, 证明其正确性.第4节提出各类观测不确定同时存在的情况下, 可诊断性的判定方法.第5节对观测不确定条件下可诊断性判定的时间复杂度进行分析.第6节给出相关工作的比较分析.第7节总结本文的工作, 并对未来进一步可能的研究进行展望.
1 离散事件系统的可诊断性 1.1 离散事件系统诊断离散事件系统是由异步、突发的事件驱动状态演化的动态系统, 其状态只取有限个离散值[3].通常采用有限状态自动机对离散事件系统进行建模.
定义1(离散事件系统模型)[1].离散事件系统模型通常用有限状态自动机G=(X, Σ, δ, x0) 来表示, 其中, X是有限状态集合, Σ是可能发生的有限事件集合, δ⊆X×Σ×X是有限状态转移集合, x0是初始状态.
自动机状态在事件触发下的转移序列称为路径, 记为p=(x1, e1, x2, …, en-1, xn), 任意i∈{1, …, n-1}, 有 (xi, ei, xi+1)∈ δ.若x1=xn, 则称为环路.事件序列称为轨迹, 记为σ=e1e2…en-1.|σ|表示轨迹的长度, 即轨迹中事件的个数.ε表示空轨迹, Σ*表示Σ中所有有限事件序列 (包含ε) 的集合.从初始状态开始所有轨迹的集合称为自动机语言, 记为L(G).显然, L(G)⊆Σ*且前缀封闭.L(G, x)⊆L(G) 表示终止于状态x的语言.
根据事件性质, 将事件集合Σ划分为3个独立子集:Σo是可观测事件集, Σu是正常 (不可观测) 事件集, Σf是故障 (不可观测) 事件集.观测函数
| $\begin{array}{*{20}{l}} {{P_o}(\sigma ) = \sigma ,\sigma \in {\Sigma _o},}&{{P_o}(\sigma ) = \varepsilon ,\sigma \in \Sigma - {\Sigma _o},}\\ {{P_o}(\varepsilon ) = \varepsilon ,}&{{P_o}(\sigma e) = {P_o}(\sigma ){P_o}(e),\sigma \in {\Sigma ^*},e \in \Sigma .} \end{array}$ |
类似地, 故障函数
| $\begin{array}{*{20}{l}} {{P_f}(\sigma ) = \{ \sigma \} ,\sigma \in {\Sigma _f},}&{{P_f}(\sigma ) = \emptyset ,\sigma \in \Sigma - {\Sigma _f},}\\ {{P_f}(\varepsilon ) = \emptyset ,}&{{P_f}(\sigma e) = {P_o}(\sigma ) \cup {P_o}(e),\sigma \in {\Sigma ^*},e \in \Sigma .} \end{array}$ |
定义2(离散事件系统诊断问题)[15].离散事件系统的诊断问题可表示为一个二元组 (G, O), 其中, G是DES的模型; O是观测, 即系统运行时实际观测到的事件序列.
定义3(候选诊断)[15].离散事件系统诊断问题 (G, O) 的候选诊断是一个二元组
DES的诊断, 其实质是根据在线观测事件序列, 在离线模型中寻找相容轨迹, 从而推测系统所处的状态以及是否有故障发生.在一般情况下, 一个诊断问题可能存在多个候选诊断.因此, 其诊断结果是一个候选诊断集.如果两个候选诊断的故障集不一致, 则称存在冲突.冲突候选诊断的存在, 将导致无法正确检测和孤立故障.一方面, 我们会采取进一步的观测, 以期待排除候选诊断之间的冲突; 另一方面也会问:进一步观测是否一定可以排除候选诊断之间的冲突?离散事件系统可诊断性可以回答这个问题.
1.2 离散事件系统可诊断性文献[1]首次从事件发觉的角度来定义离散事件系统的可诊断性, 其具体定义如下.
定义4(可诊断性)[1].离散事件系统G=(X, Σ, δ, x0) 是可诊断的, 当其满足如下条件:
| $\begin{array}{c} (\forall f \in {\Sigma _f})(\exists n \in N)(\forall \sigma \in {{\bar L}_G}(f))(\forall \sigma ' \in L(G)/\sigma ,|{P_o}(\sigma ')| \ge n),\\ (\forall l \in L(G)),{P_o}(l) = {P_o}(\sigma \sigma ') \Rightarrow l \in {L_G}(f). \end{array}$ |
其中, L(G)/σ={Σ'∈Σ*|σσ'∈L(G)}表示轨迹σ的后继语言, LG(f)=(Σ*fΣ*)
其直观含义是:如果系统可诊断, 那么任意故障发生后, 只要后继经过足够长的观测 (n步的延时观测), 一定能探测到该故障的发生.换句话说, 任意故障发生之后, 总能产生不一样的观测, 使得可以诊断出其类型.
上述定义基于两个假设:(1) 系统是活的 (live), 即, 系统的运行是不会终止的; (2) 不存在不可观测事件环路, 即不存在一条环路, 其所有事件均为不可观测事件[1].假设 (1) 是为了简化问题, 经过适当调整可以放弃这一假设; 假设 (2) 是为了保障观测的顺利进行, 如果存在不可观测事件环路, 系统的状态转换可能会陷入一个无穷的不可观测事件环路, 进而无法正常获取观测.它们被大多数文献普遍采用[1, 11, 14], 本文也继续沿用这两个假设.
文献[11]提出了一种可诊断性判断的多项式时间复杂度算法——双树算法.该方法的具体过程如下:(1) 构造预诊断器; (2) 将预诊断器进行自同步, 得到同步自动机; (3) 在同步自动机上检测是否具有故障冲突的环路, 若不存在这样的环路, 则系统可诊断, 否则不可诊断.接下来形式化上述过程.
定义5(预诊断器)[11].离散事件系统G=(X, Σ, δ, x0) 的预诊断器是在G的基础上构造的一个非确定性有限状态自动机
●Go的有限状态集合Xo={(x, F)|x∈X1, F⊆Σf}∪{(x0, ∅)}, 其中, X1={x∈X|∃(x', e, x)∈δ, e∈Σo}, G中通过某个可观测事件发生转移所达状态的集合, F=Pf(σ), ∃σ∈L(G, x), 即存在从x0到x的轨迹, F为该轨迹上的故障集合.
●Go的有限事件集合为Σo, 即G的可观测事件集合.
●Go的有限状态转移集合δo⊆Xo×Σo×Xo, ((x, F), e, (x', F'))∈δo当且仅当G中存在一条路径 (x, e1, x1, …, en, xn, e, x'), n≥0, Po(ei)=ε, 对任意i∈{1, 2, …, n}, Po(e)=e, 而且
●
从预诊断器的构造可知, 其实质上是抽取出原始自动机中的可观测事件所能到达的状态, 为其加上故障标签, 并重建其状态转换过程而形成的新自动机.由于事件全部为可观测事件, 因此通常也被称为可观测自动机.
定义6(自同步自动机)[11].预诊断器
●
●Σo是可观测事件集合, 其作为Gd的有限事件集合;
●δd⊆XdxΣo×Xd是Gd的有限状态转移集合,
●
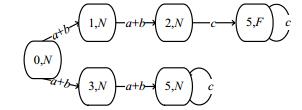
例1:图 1(a)为一个简单的离散事件系统模型, 图中的节点表示系统状态, 节点之间的有向边表示状态的转移, 其中, 状态集合X={0, 1, 2, 3, 4, 5}, 初始状态x0=0, 可观测事件集合Σo={a, b, c}, 正常事件集合Σu={u}, 故障事件集合Σf={f}.其预诊断器如图 1(b)所示, 由于系统只有一个故障事件f, 为简单起见, 我们用N=∅表示没有故障发生, 用F={f}表示故障f发生, 后续例子中将继续采用这种方式.其自同步自动机如图 1(c)所示.根据双树算法, 离散事件系统是可诊断的, 因为自同步自动机的环路中都没有出现故障冲突.如果观测到事件序列abc, 即可判断发生了故障; 如果观测到事件序列bac, 即可判断系统运行正常.
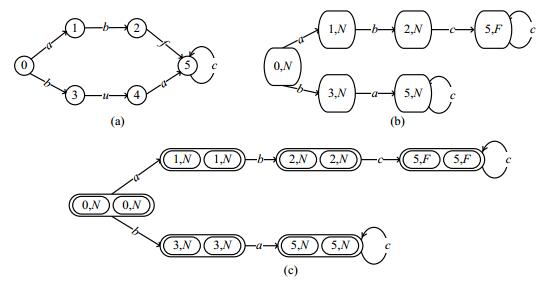
|
Fig. 1 System model, pre-diagnoser and self-synchronized automaton 图 1 系统模型、预诊断器和自同步自动机 |
2 不确定观测
DES的在线诊断, 通过感知器在线观测可观测事件的发生, 然后将信息传递给诊断器, 诊断器在离线模型中寻找与观测相容轨迹, 从而给出诊断结果.通常假定观测是确定的, 即任意行为轨迹发生后, 其可观测事件序列与实际观测到的事件序列一致.而在实际应用中, 要获取确定观测却很困难, 这极大地限制了诊断方法的适用范围.Lamperti和Zanella根据导致观测不确定的原因, 将观测不确定分为4类:时序不确定、丢失不确定、逻辑不确定和来源不确定[12].
2.1 时序不确定离散事件系统的事件发生是异步的, 即事件的发生有严格的时间先后顺序.但在实际观测时, 由于信息传输方面的原因, 可能会导致事件时序的丢失, 从而无法确定事件发生的先后顺序, 在文献[12]中称其为时序不确定.
在文献[12]中, 通过 (有向无环) 观测图来表示时序不确定观测.在离线判断可诊断性时, 可能并无实际的观测, 无法给出观测图.因此, 我们假定时序不确定仅存在发生时间点临近的若干可观测事件之间.这一假定基于如下考虑:两个事件如果彼此发生的时间间隔太长, 即使在传输过程中会有延时, 也不足以导致时序变化.
我们用e∈σ表示轨迹σ中包含事件e, 用σ'⊆σ表示轨迹σ'是σ的子轨迹.
定义7(相对时间). 给定离散事件系统G中的一条轨迹σ, 事件e1, e2∈σ, 它们沿轨迹σ发生的时间点分别为x1和x2, 则定义|x1-x2|为e1和e2在轨迹σ中的相对时间, 记为RTσ(e1, e2).
相对时间的值域为[1, ∞), 且为整数.当相对时间为1时, 二者连续发生.在此基础上定义时序不确定度.
定义8(时序不确定度). 令可能丢失时序的可观测事件之间的最大相对时间为d, 时序不确定度为 (d+1).
定义9(疑似片段集). 给定离散事件系统G和时序不确定度n, 所有可能会丢失时序的可观测事件序列称为疑似片段集, 记为
| $\begin{align} & \Sigma _{n}^{//}(G)=\{{\sigma }'|(\forall e\in {\sigma }'.e\in {{\Sigma }_{o}})\wedge (\exists {{e}_{1}},{{e}_{2}}\in {\sigma }'.{{e}_{1}}\ne {{e}_{2}})\wedge \\ & (\exists \sigma .{\sigma }'={{P}_{o}}(\sigma )\wedge \forall {{e}_{1}},{{e}_{2}}\in {\sigma }'.R{{T}_{\sigma }}({{e}_{1}},{{e}_{2}})n)\} \\ \end{align} $ |
由定义9可知,
定义10(时序扩展). 疑似片段发生后, 实际可能观测到的事件序列是其中所有原子事件的一个排列.疑似片段中所有原子事件的全排列, 称为其时序扩展, 记为
将其扩展到任意可观测事件序列
| $E_o^{//}(\sigma ,\Sigma _n^{//}(G)) = \left\{ {\begin{array}{*{20}{l}} {\{ \sigma \} ,{\rm{ }}\neg \exists \sigma '.(\sigma ' \subseteq \sigma \wedge \sigma ' \in \Sigma _n^{//}(G))}\\ {\bigcup\limits_{\sigma = {\sigma _1}\sigma '{\sigma _2}} {E_o^{//}({\sigma _1},\Sigma _n^{//}(G))} \times {E^{//}}(\sigma ') \times E_o^{//}({\sigma _2},\Sigma _n^{//}(G)),{\rm{ }}\sigma ' \in \Sigma _n^{//}(G)} \end{array}} \right.$ |
其中, “x”为笛卡尔积.
易证,
感知器探测到可观测事件的发生之后, 将信息传输给诊断器的过程中, 由于信息传输方面的原因, 可能 (但不一定) 会导致信息丢失, 从而无法确定该事件是否发生了.在文献[12]中将这种情况称为丢失不确定.
在文献[12]中, 处理这类不确定观测条件下的诊断时, 事先就给定了可能会丢失的可观测事件, 即在允许某些事件丢失的情况下进行诊断.我们将可能会丢失的可观测事件集称为疑似丢失事件集, 记为Σε.
定义11(丢失扩展). 对任意e∈Σε, 其发生之后观测到的信息可能是e或者ε.令Eε(e)={e, ε}, 称为事件e的丢失扩展.
给定Σε, 定义任意可观测事件序列
| $E_o^\varepsilon (\sigma ,{\Sigma ^\varepsilon }) = \left\{ {\begin{array}{*{20}{l}} {\{ \sigma \} ,{\rm{ }}\neg \exists e.(e \in \sigma \wedge e \in {\Sigma ^\varepsilon })}\\ {\bigcup\limits_{\sigma = {\sigma _1}e{\sigma _2}} {E_o^\varepsilon ({\sigma _1},{\Sigma ^\varepsilon })} \times {E^\varepsilon }(e) \times E_o^\varepsilon ({\sigma _2},{\Sigma ^\varepsilon }),{\rm{ }}e \in {\Sigma ^\varepsilon }} \end{array}} \right.$ |
某一事件发生之后, 通过感知器感知到其发生, 然后通过传输通道传输给诊断器.在这个过程中, 由于感知器的精度或者传输过程中的信息失真, 可能会导致诊断器接受到的并不是该事件发生的信息, 而可能是另一事件发生的信息.文献[12]中将这种情况称为逻辑不确定.文献[12]中, 用逻辑复合事件来表示.
定义12(逻辑复合事件)[15].可观测事件a, b∈Σo, 若在观测过程中无法确切区分, 则用a||b来表示, 称为逻辑复合事件.
这里定义了两个事件的逻辑复合事件, 其可推广为任意有限个事件的情形.甚至是可观测事件与空事件之间的逻辑不确定, 例如a||ε, 表示事件a发生与否无法确定.注意a||ε与a∈Σe之间的区别, 虽然都表示事件a与ε之间的不确定:前者表示a发生与否无法确定, 既有可能事件a发生了, 但观测系统没有观测到, 也有可能事件a根本没有发生, 由于感知器的噪声导致观测系统误认为它发生了; 后者表示事件a确实发生了, 但可能由于信息丢失导致观测系统没有观测到其发生.
在文献[12]中, 处理逻辑不确定观测条件下的诊断时, 事先给定了逻辑复合事件.即假定根据事件信息之间的相似度或感知器精确度可以预判哪些事件可能存在逻辑不确定.逻辑复合事件的集合, 记为Σ||.
定义13(逻辑扩展).逻辑复合事件中某个原子事件发生后, 可能观测到其中的任一事件.我们将逻辑复合事件中所有原子事件的集合称为其逻辑扩展, 记为E||(E), E∈Σ||.
给定Σ||, 可定义任意可观测事件序列
| $E_o^{||}(\sigma ,{\Sigma ^{||}}) = \left\{ {\begin{array}{*{20}{l}} {\{ \sigma \} ,{\rm{ }}\neg \exists e.[e \in \sigma \wedge e \ne \varepsilon \wedge \exists E.E \in {\Sigma ^{||}} \wedge e \in {E^{||}}(E)]}\\ {\bigcup\limits_{\sigma = {\sigma _1}e{\sigma _2}} {E_o^{||}({\sigma _1},{\Sigma ^{||}})} \times {E^{||}}(E) \times E_o^{||}({\sigma _2},{\Sigma ^{||}}),{\rm{ }}\exists E.E \in {\Sigma ^{||}} \wedge e \in {E^{||}}(E) \wedge e \ne \varepsilon } \end{array}} \right.$ |
注意:由于存在可观测事件与空事件之间的逻辑不确定, 经过逻辑扩展, 可能观测到超过原有长度的事件序列, 这使得逻辑扩展观测的计算非常复杂.例如, a||ε∈Σ||, 则空事件序列ε经过扩展之后的观测集为{ε, a, aa, …}.为简单起见, 只计算长度不超过原有长度的事件序列.这样,
当系统由多个不同的组件构成时, 不同的组件中可能会发生相同的事件, 观测系统观测到某个事件后, 可能无法确定该事件来源于哪个组件.文献[12]中, 把这种情况称为来源不确定.通过采用不同的感知器监测不同的组件, 在诊断器中记录信息来源 (感知器ID), 即可消除这种观测不确定.因此, 在本文中不考虑来源不确定.
3 不确定观测下的可诊断性各类观测不确定, 会给离散系统的诊断造成影响.传统的可诊断性定义已不适用于不确定观测条件下系统的可诊断性刻画.我们将扩展可诊断性的定义, 并分别给出各类不确定观测条件下判定可诊断性的方法.
3.1 不确定观测下的可诊断性定义14(不确定观测下的可诊断性).离散事件系统G=(X, Σ, δ, x0), 在存在不确定观测集
| $\begin{array}{c} (\forall f \in {\Sigma _f})(\exists n \in N)(\forall \sigma \in {{\bar L}_G}(f))(\forall \sigma ' \in L(G)/\sigma ,|{P_o}(\sigma ')| \ge n),\\ (\forall l \in L(G)),E_o^u({P_o}(l),\Sigma _o^u) \cap E_o^u({P_o}(\sigma \sigma '),\Sigma _o^u) \ne \emptyset \Rightarrow l \in {L_G}(f). \end{array}$ |
不确定观测集
我们将分别给出各类不确定观测下的可诊断性判定方法, 它们都通过扩展传统的双树方法来实现.具体而言, 就是针对各类不确定观测, 分别构造不同的预诊断器, 然后通过预诊断器的自同步来实现可诊断性的判定.
3.2 时序不确定观测下的可诊断性判定定义15(预诊断器I).通过扩展离散事件系统G的预诊断器
●
●
●
●
其中,
算法1.疑似片段的显式时序扩展.
输入:疑似片段路径 (x1, e1, x2, e2, …, en-1, xn).
输出:有向图G=(V, E).
1.Initial: G=(V, E), V={(xi, 1) |=1, 2, …, n}, E={[(xi, 1), ei, (xi+1, 1) ]|=1, 2, …, n-1}, Σ={e1, e2, …, en} //(xi, m) 表示状态点xi的第m个副本; Σ是疑似片段中事件的多重集
2.for i=1 to n-1 //依次确定第i层节点的后续节点
3.compute m //m是第i层节点的个数, 即xi的副本数
4.for j=1 to m//依次确定 (xi, j) 的后续节点
5.compute Σ' of (xi, j) //计算 (xi, j) 的前驱事件多重集
6.for each e∈Σ-Σ'//确定 (xi, j) 通过事件e转换之后的后续节点
7.compute k //k是第 (i+1) 层当前节点的个数
8.if ¬∃j'.[(xi, j), e, (xi+1, j')]∈E
//如果 (xi, j) 找不到通过事件e转换之后的后续节点 (简称e后续)
9.if ∃r[(xi, q), e', (xi+1, r)]∈E
//如果在第 (i+1) 层的当前节点中可以找到节点直接添加e边成为 (xi, j) 的e后续
10.E=E∪{[(xi, j), e, (xi+1, r)]} //添加边
11.else
12.V=V∪{(xi+1, k+1) }//添加xi+1的新副本 (xi+1, k+1)
13.E=E∪{[(xi, j), e, (xi+1, k+1) ]}//添加边
14.Return G
由算法1可知, 疑似片段的路径 (x1, e1, x2, e2, …, en-1, xn) 扩展之后变成有向图G=(V, E).G满足如下性质.
●任意两点之间的任意两条不同路径都满足:路径上的事件多重集是相同的, 但是顺序不同;
●{e1, e2, …, en}的每一种排列都有一条从x1到xn路径上的事件序列与其一致.
可能会添加若干状态点, 它们是疑似片段路径上状态点的复制.为区分不同副本, 用 (xi, m) 来标记, 即xi的第m个副本.之所以复制而不引进新的状态点, 是因为时序不确定并没有改变系统的状态转换过程, 仅仅是改变了观测所得事件序列的顺序.
令N为疑似片段路径上状态点的个数, 若疑似片段中没有相同的事件, 则扩展之后各状态点的副本数正好与杨辉三角第N行的数一致.根据杨辉三角的性质可知, G的节点数为2N-1, 即相对于原有状态数成指数级别的膨胀.又由于N≤n, 其中, n为时序不确定度, 故有G的节点数不超过2n.
Go中的所有疑似片段路径都通过算法1进行扩展, 即得到预诊断器
例2:在图 1(a)所示的自动机G中, 令时序不确定度为2, 则
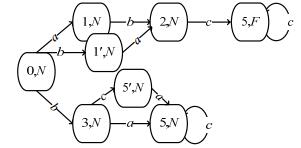
|
Fig. 2 Pre-Diagnoser |
|
Fig. 3 Self-Synchronized automaton |
为了证明上述判定方法的正确性, 我们先给出下面的两个引理.
引理1.在自动机
| $p = \left( {\left( {{x_0},{\rm{ }}\emptyset } \right),{e_0},{\rm{ }}\left( {{x_1},{F_1}} \right),{\rm{ }} \ldots ,{\rm{ }}\left( {{x_k},{F_k}} \right),{e_k},{\rm{ }} \ldots ,{\rm{ }}\left( {{x_n},{F_n}} \right),{e_n},{\rm{ }}\left( {{x_k},{F_k}} \right)} \right),$ |
都有:
(1)Fi=Fj对任意的i, j∈{k, k+1, …, n};
(2)∃uv*∈L(G), 满足
证明:由
(1) 由
| ${F_k} = {F_k}_{ + 1} = \ldots = {F_n}.$ |
(2) 当路径p中的所有状态点都来自Xo时, 有∃uv*∈L(G), 满足Po(u)=e0…ek-1, Po(v)=ek…en, Pf(u)=Pf(uv)=Fk, 这个结论在文献[11]中已给出.
当路径p中的部分状态点来自
| $(({x_i},{F_i}),{e_i},({x'_{i + 1}},{F'_{i + 1}}),{e_{i + 1}},...,({x'_{i + j}},{F'_{i + j}}),{e_{i + j}},({x_{i + j + 1}},{F_{i + j + 1}}))$ |
的子序列 (其中,
| $(({x_i},{F_i}),{e'_i},({x_{i + 1}},{F_{i + 1}}),{e'_{i + 1}},...,({x_{i + j}},{F_{i + j}}),{e'_{i + j}},({x_{i + j + 1}},{F_{i + j + 1}}))$ |
其中,
因为
因此, 对于任意p有如下结论:∃uv*∈L(G), 满足
| ${P_f}\left( {uv} \right) = {F_k}.$ |
引理中的 (1) 说明
引理2.在自同步自动机
| $p = (x_0^d,{e_0},x_1^d,...,x_k^d,{e_k},...,x_n^d,{e_n},x_k^d),,x_i^d = ((x_i^1,F_i^1),(x_i^2,F_i^2)),i = 1,2,...,n$ |
都有:
(1)在
| $\begin{array}{l} {p_1} = (({x_0},\emptyset ),{e_0},(x_1^1,F_1^1),...,(x_k^1,F_k^1),{e_k},...,(x_n^1,F_n^1),{e_n},(x_k^1,F_k^1)),\\ {p_2} = (({x_0},\emptyset ),{e_0},(x_1^2,F_1^2),...,(x_k^2,F_k^2),{e_k},...,(x_n^2,F_n^2),{e_n},(x_k^2,F_k^2)). \end{array}$ |
(2)
证明:由自同步自动机的定义和引理1可以证明.
引理2说明,
定理1.给定
证明:下面将分别证明其必要性和充分性.
(1) 先证:如果G可诊断, 则
假设
| $\begin{array}{l} {p_1} = (({x_0},\emptyset ),{e_0},(x_1^1,F_1^1),...,(x_k^1,{F^1}),{e_k},...,(x_n^1,{F^1}),{e_n},(x_k^1,{F^1})),\\ {p_2} = (({x_0},\emptyset ),{e_0},(x_1^2,F_1^2),...,(x_k^2,{F^2}),{e_k},...,(x_n^2,{F^2}),{e_n},(x_k^2,{F^2})). \end{array}$ |
由引理1可知, 存在
| $\begin{array}{l} {e_0}...{e_{k - 1}} \in E_o^{//}({P_o}({u_1}),\Sigma _n^{//}(G)),{e_k}...{e_n} \in E_o^{//}({P_o}({v_1}),\Sigma _n^{//}(G)),{P_f}({u_1}) = {P_f}({u_1}{v_1}) = {F^1},\\ {e_0}...{e_{k - 1}} \in E_o^{//}({P_o}({u_2}),\Sigma _n^{//}(G)),{e_k}...{e_n} \in E_o^{//}({P_o}({v_2}),\Sigma _n^{//}(G)),{P_f}({u_2}) = {P_f}({u_2}{v_2}) = {F^2}. \end{array}$ |
故有
| $E_o^{//}({P_o}({u_2}v_2^m),\Sigma _n^{//}(G)) \cap E_o^{//}({P_o}(\sigma tv_1^m),\Sigma _n^{//}(G)) \ne \emptyset $ |
但
(2) 再证:如果
由不存在故障冲突的环路可知,
| $\begin{array}{c} (\forall f \in {\Sigma _f})(\forall \sigma \in {{\bar L}_G}(f))(\forall \sigma ' \in L(G)/\sigma ,|{P_o}(\sigma ')| \ge (|X_d^{//}| - 1)),\\ (\forall l \in L(G)),E_o^{//}({P_o}(l),\Sigma _n^{//}(G)) \cap E_o^{//}({P_o}(\sigma \sigma '),\Sigma _n^{//}(G)) \ne \emptyset \Rightarrow l \in {L_G}(f). \end{array}$ |
根据可诊断性的定义 (定义14) 可知, G是可诊断的, 充分性得证.
3.3 丢失不确定观测下的可诊断性分析定义16(预诊断器Ⅱ).通过扩展离散事件系统G的预诊断器
●
●
●
| $\delta _o^\varepsilon = {\delta _o} \cup \{ (x,\varepsilon ,x')|\exists e \in {\Sigma _o},(x,e,x') \in {\delta _o} \wedge e \in {\Sigma ^\varepsilon }\} $ |
●
从上述构造过程可知,
同样地, 通过预诊断器
定义17(自同步自动机Ⅱ).可观测自动机
●
●
●δd⊆XdxΣo×Xd是
①
②
●
通过修改同步自动机中的同步策略 (在δd中引入针对ε事件的同步策略), 实现丢失事件发生之后的状态与该事件未发生前的状态之间的同步.定理2证明了在丢失不确定条件下可诊断性判定方法的正确性.
定理2.在给定疑似丢失集Σε的条件下, G可诊断, 当且仅当
证明:这里有一点要特别说明.由于空事件ε的引入,
在
在空事件环情况下, 定理2的必要性证明思路如下:如果存在故障冲突的空事件环, 那么在
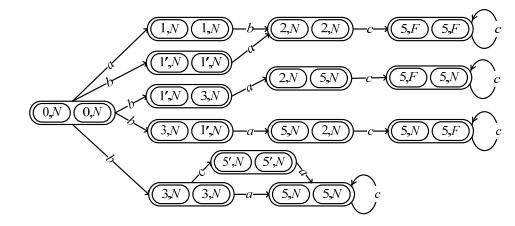
例3:在图 1(a)所示的自动机G中, 考虑疑似丢失事件集{a}, 则其预诊断器
|
Fig. 4 Pre-Diagnoser |

|
Fig. 5 Self-Synchronized automaton |
3.4 逻辑不确定观测下的可诊断性分析
定义18(预诊断器Ⅲ).通过扩展离散事件系统G的预诊断器
●
●
●
●
从构造过程可知,
类似地, 通过构造自同步自动机
定理3.在给定逻辑不确定观测集Σ||的条件下, G可诊断, 当且仅当
证明:其证明与定理2的证明类似.
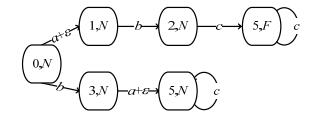
例4:在图 1(a)所示的自动机G中, 考虑逻辑复合事件集{a||b}, 则其预诊断器
|
Fig. 6 Pre-Diagnoser |

|
Fig. 7 Self-Synchronized automaton |
4 复合不确定观测下的可诊断性
上一节我们分别讨论了在时序不确定、丢失不确定和逻辑不确定观测条件下的离散事件系统可诊断性问题.但在实际应用中, 这几类不确定性问题可能同时存在.下面我们将探讨同时存在这些观测不确定性的情况下, 可诊断性的判定方法.从上一节的分析可知, 虽然导致观测丢失不确定和逻辑不确定的原因不同, 但对逻辑不确定中的空事件ε采用非对称的处理后, 丢失不确定可以看做逻辑不确定的特例, 因此, 我们只讨论时序不确定和逻辑不确定混合的情况.
当观测中同时存在时序不确定和逻辑不确定时, 情况会变得非常复杂.因为这些不确定性会发生相互正交作用[12], 导致更复杂的观测不确定性.例如, 如果
定义19(复合扩展观测). 给定
| $E_o^u(\sigma ,\Sigma _o^u) = \bigcup\limits_{\sigma ' \in E_o^{||}(\sigma ,{\Sigma ^{||}})} {E_o^{//}(\sigma ',\Sigma _n^{//}(G) \times {\Sigma ^{||}})} $ |
其中,
由定义可知, 复合扩展观测是先考虑逻辑扩展, 然后再考虑时序扩展.例如, 令
| $\Sigma _2^{//}(G) \times {\Sigma ^{||}} = \{ ab,ac\} ,E_o^u(ab,\Sigma _o^u) = \{ ab,ba,ac,ca\} $ |
因为逻辑不确定扩展可能在σ'中引入空事件ε, 为了保障构造出的预诊断器的正确性, 在计算疑似片段的逻辑扩展时做了一定的技术处理.例如,
在此基础之上, 我们提出复合不确定观测下的可诊断性判断方法, 其主要过程如下:
(1)按照预诊断器Ⅲ的定义构造G在逻辑复合事件集Σ||下的预诊断器
(2)根据时序不确定度n, 计算G的疑似片段集
(3)按照预诊断器Ⅰ的定义构造
(4)由于空事件ε的引人, 按照自同步自动机Ⅱ的定义进行自同步, 得到同步自动机
(5)在同步自动机上测试是否具有故障冲突的环路:若不存在这样的环路, 则系统可诊断; 否则, 不可诊断.
5 复杂性分析与经典的双树方法类似, 在各类观测不确定条件下, 可诊断性判定的时间复杂度主要由如下3个过程构成:
(1)预诊断器的构造;
(2)同步自动机的构造;
(3)同步自动机中是否具有故障冲突环路的判断.
在经典双树方法中, 预诊断器的状态数最大为
●|X|为离散事件系统的状态数, |Σo|和|Sf|分别为系统的可观测事件数和故障事件数;
●同步自动机的状态数最大为
因此, 第 (1) 步的时间复杂度为
在处理时序不确定时, 由于在构造预诊断器的过程中添加了若干状态点, 因此其时间复杂度变为
| $O\left( {{{\left| {X'} \right|}^4}x\left| {{\Sigma _o}} \right| \times |{\Sigma _f}|} \right),$ |
其中, |X'|是疑似片段显式扩展所得预诊断器的状态数.由疑似片段的显式扩展算法1可知, |X'|是O(|X|×2n) 级别的, 其中, n为时序不确定度.因此, 总体的时间复杂度为O(24n×|X|4×|Σo|x|Σf|).显然, 时序不确定度越高, 疑似片段就越多, 要添加的状态点也就越多, 可诊断性判定方法的效率就越低.但在时序不确定度较低时, 可以认为其效率与经典双树效率相当.在实际应用中, 可以通过先采取较低的时序不确定度, 然后再逐渐增加的方式来控制时间复杂度的增长.
在处理丢失不确定和逻辑不确定性时构造的预诊断器, 与经典双树方法相比, 状态数均是O(|X|) 级别的; 虽然添加了一些状态转换边, 但是由于可选边仅限于Σo∪{ε}中的边, 其状态转移最大数依然是O(|X|2×|Σo|) 级别的.因此, 总体时间复杂度依然为O(|X|4×|Σo|x|Σf|).
综上所述, 仅考虑单类观测不确定条件下可诊断性的判定, 从时间复杂度的角度来看, 时序不确定要比丢失不确定和逻辑不确定复杂.在多类观测不确定正交复合的情况下, 虽然丢失不确定或逻辑不确定会导致出现时序不确定的疑似片段增加, 但都是在时序不确定度允许的范围内, 因此, 其时间复杂度与仅考虑时序不确定时可诊断性的判断属于同一复杂度级别的.
6 相关工作下面我们介绍与本文研究内容密切相关的主要相关工作, 并从系统模型、不确定性表示和解决问题的思路等方面进行比较分析.
Lamperti等人在主动系统 (active system) 中讨论了在各类观测不确定条件下, 系统的诊断问题[12, 16].主动系统是一类特殊的离散事件系统, 一个主动系统由一个在输入输出终端之间由链相互连接的组件集构成.正因为存在多个组件, 所以他们讨论了来源不确定对系统诊断的影响, 这是本文没有考虑的.他们通过有向无环图 (观测图) 来表示各种观测不确定:观测图中的节点是事件的集合, 集合中的多个事件之间存在丢失不确定或逻辑不确定; 节点之间的有向边表示时序先后关系, 不存在路径连接的节点之间时序是不确定的.通过观测图, 可以获得不确定观测的扩展观测, 从而将不确定观测的条件下的诊断问题转换成若干与之对应的确定观测下的诊断问题, 最终实现系统的诊断.他们只讨论了观测不确定条件下的诊断问题, 并未讨论可诊断性问题.其诊断是在线进行的, 可以根据实际观测得到观测图.但本文的可诊断性判定是离线进行的, 无法事先获取观测图, 因此我们采用在一定时序不确定度条件下猜测疑似失序片段的方式来处理时序不确定性.其通过不确定观测扩展, 将不确定观测下的诊断问题转换为若干确定观测下的诊断问题的思路, 对本文产生了重要影响.
吉林大学欧阳丹彤教授的研究团队在离散事件系统的诊断方法和可诊断性判定方面做了大量的研究工作[5, 6, 9], 其中, 文献[6]研究了不完备离散事件系统的可诊断性, 文献[9]研究了不完备离散事件系统的诊断方法.他们主要考虑了两类不完备性:时序不完备和行为不完备.虽然模型不完备性和观测不确定性都致力于扩展离散事件系统诊断方法的适用性和实用性, 但两者的着眼点不同.模型不完备性考虑的是由于系统建模不完善, 导致即使观测确定也无法在系统模型中找到相容的事件轨迹, 其研究着眼于降低系统建模的难度.而我们的研究假定系统模型是完备的, 而允许系统观测是不确定的, 着眼于减低观测系统的构建难度.系统模型的不完备, 通过在线观测与离线模型的对比才能发现, 因此, 不完备离散事件系统的可诊断性判定是在线进行的, 而本文讨论的观测不确定条件下的可诊断性是离线进行的.
Grastien等人在文献[13, 14]中分别将离散事件系统的可诊断性判断和诊断转换成可满足性问题 (satisfiability problem, 简称SAT), 然后通过调用SAT求解器来实现可诊断性的判定和系统诊断.他们采用简洁表示系统 (succinct system representation)[13, 14]对离散事件系统建模.与我们采用的有限状态自动机 (定义1) 相比, 简洁表示系统在表达上更简洁:它通过状态变量集而不是状态集来描述系统状态, 通过对n个逻辑状态变量的不同赋值, 可以表示2n个不同的状态; 它通过定义事件的转换函数来描述系统状态的转换, 而不是显示地列举出所有状态之间的转换过程.事件e的转换函数δ(e) 是若干< φ, c > 对的集合, 说明事件e在条件φ满足的条件下可执行, 产生效果为c.采用简洁表示系统一方面便于将离散事件系统的诊断问题转换为SAT问题, 另一方面也能表示事件的并行.在某个状态不同事件的执行条件相互不矛盾, 执行效果也相互不冲突, 就可以并发执行.事件的并发执行, 实质上对应时序不确定的情况.文献[13]将双树算法[11]判定可诊断性的思路编码成一个逻辑公式, 从而将系统的可诊断性问题转化为该公式的可满足性问题.由于其允许事件的并行, 所以其处理了时序不确定条件下的可诊断性判断问题.但其不能处理逻辑不确定或丢失不确定条件下的可诊断性判断问题.
Su等人在文献[15]中也对观测不确定条件下的可诊断性展开了研究.和我们一样, 他们也采用有限状态自动机构造系统模型.但他们只分别研究了时序不确定和逻辑不确定, 而本文对时序不确定、丢失不确定和逻辑不确定都分别做了研究, 而且对复合观测不确定的情况也做了研究.在处理时序不确定和逻辑不确定时, 两者在技术路线上有很大的差异, 尽管大家都是通过扩展双树算法来实现的.在处理时序不确定时, 两者在时序不确定度和时序扩展的定义上都不相同, 进而预诊断器的构造也各不同, 最终导致可诊断性判断的时间复杂度也不同.我们定义的时序不确定度以事件发生的相对时间为依据, 更加合理.他们方法的时间复杂度为O(|X|4×|Σo|l×|Σf|), 其中, l是时序不确定水平[15]; 而我们的时间复杂度为O(24n×|X|4×|Σo|x|Σf|), 其中, n是时序不确定度.我们的算法在时序不确定度较低和可观测动作数量较大时性能要更好一些.在处理逻辑不确定时, 两者在预诊断器的构造和同步策略上也都不同.导致这些不同的主要原因在于对如何排除干扰环路的技术处理上.为了避免干扰环路的出现, Su等人在预诊断器的构造上做了相当复杂的技术处理[15]; 而本文则着眼于同步策略的修改.虽然大家的时间复杂度均为O(|X|4×|Σo|x|Σf|), 但是在构造的预诊断器中, 他们的方法无论是节点数还是边数均大于我们的方法, 因此, 我们方法的实际效率要高一些.而且本文对各类观测不确定的处理方式更有利于处理复合观测不确定, 这一点在本文第4节已有所体现.
7 结论与展望离散事件系统可诊断性的研究出于简单性考虑, 大都假定系统观测是确定的.但在实际应用中, 由于信息传输以及感知器的精度等原因, 往往很难获取到确定的观测信息.这给系统的可诊断性判定带来了困难.本文扩展了传统可诊断性的定义, 给出观测不确定条件下的可诊断性定义, 并给出其判定方法.
与观测确定条件下的可诊断性相比, 在观测不确定条件下的可诊断性判断的效率会有所下降, 特别是包含时序不确定时.但是, 这里的可诊断性判断都是在离线情况下进行的, 因此我们认为, 从降低观测系统的建设成本以及提高诊断系统的鲁棒性来看, 这种效率上的牺牲是值得的.
基于双树方法的可诊断性判定, 其时间复杂度虽然只有系统状态数的多项式级别, 但在系统规模很大时, 其效率依然显得不高.因此, 下一步将研究在分布式MBD中观测不确定条件下的可诊断性判定方法, 以适应大规模系统可诊断性判定的需求.
| [1] | Sampath M, Sengupta R, Lafortune S, Sinnamohideen K, Teneketzis D. Diagnosability of discrete-event systems. IEEE Trans. on Automatic Control, 1995, 40(9): 1555–1575 . [doi:10.1109/9.412626] |
| [2] | Sampath M, Sengupta R, Lafortune S, Sinnamohideen K, Teneketzis D. Failure diagnosis using discrete-event models. IEEE Trans. on Control Systems Technology, 1996, 4(2): 105–124 . [doi:10.1109/87.486338] |
| [3] | Cassandras CG, Lafortune S. Introduction to Discrete Event Systems. Springer-Verlag, 2006. |
| [4] | Han X, Shi ZZ, Lin F. Research advances in model-based diagnosis. Chinese High Technology Letters, 2009, 19(5): 543–550 (in Chinese with English abstract). [doi:10.3772/j.issn.1002-0470.2009.05.018] |
| [5] | Zhao XF, Ouyang DT. Progress on model-based diagnosis of discrete-event systems. Journal of Frontiers of Computer Science and Technology, 2011, 5(2): 114–127 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-KXTS201102004.htm |
| [6] | Wang XY, Ouyang DT, Zhao XF. Diagnosability of discrete event systems with an incomplete model. Ruan Jian Xue Bao/Journal of Software, 2015, 26(6): 1373–1385 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4585&journal_id=jos [doi:10.13328/j.cnki.jos.004585] |
| [7] | Zhao XF, Ouyang DT. Model-Based diagnosis of discrete event systems with an incomplete system model. In: Proc. of the 18th European Conf. on Artificial Intelligence (ECAI 2008). Patras, 2008: 189–193 . https://www.researchgate.net/profile/Xiangfu_Zhao/publication/220837178_Model-Based_Diagnosis_of_Discrete_Event_Systems_with_an_Incomplete_System_Model/links/53e43f060cf25d674e94bc18.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail |
| [8] | Kwong RH, Yeung DL. Fault diagnosis in discrete-event systems: Incomplete models and learning. IEEE Trans. on Systems, Man, and Cybernetics-Part B: Cybernetics, 2011, 41(1): 118–130 . [doi:10.1109/TSMCB.2010.2047257] |
| [10] | Lin F. Diagnosability of discrete event systems and its applications. Discrete Event Dynamic Systems, 1994, 4(2): 197–212 . [doi:10.1007/BF01441211] |
| [11] | Jiang SB, Huang ZD, Chandra V, Kumar R. A polynomial algorithm for testing diagnosability of discrete-event systems. IEEE Trans. on Automatic Control, 2001, 46(8): 1318–1321 . [doi:10.1109/9.940942] |
| [12] | Lamperti G, Zanella M. Diagnosis of discrete-event systems from uncertain temporal observations. Artificial Intelligence, 2002, 137(1-2): 91–163 . [doi:10.1016/S0004-3702(02)00123-6] |
| [13] | Rintanen J, Grastien A. Diagnosability testing with satisfiability algorithms. In: Proc. of the 20th Int'l Joint Conf. on Artificial Intelligence (IJCAI 2007). Hyderabad, 2007: 532–537 . http://www.wenkuxiazai.com/doc/4b3b0ecd050876323112128a.html |
| [14] | Grastien A, Anbulagan A, Rintanen J, Kelareva E. Diagnosis of discrete-event systems using satisfiability algorithms. In: Proc. of the 22nd National Conf. on Artificial Intelligence (AAAI 2007). Vancouver, 2007: 305–310 . https://www.researchgate.net/profile/Alban_Grastien/publication/221604979_Diagnosis_of_Discrete-Event_Systems_Using_Satisfiability_Algorithms/links/00b495180ac71cd2e6000000.pdf?origin=publication_list |
| [15] | Su XY, Zanella M, Grastien A. Diagnosability of discrete-event systems with uncertain observations. In: Proc. of the 25th Int'l Joint Conf. on Artificial Intelligence (IJCAI 2016). New York, 2016: 1265–1271 . https://www.researchgate.net/profile/Xingyu_Su/publication/305722160_Poster_for_the_IJCAI_2016_conference_paper_Diagnosability_of_Discrete-Event_Systems_with_Uncertain_Observations/links/579c129d08ae6a2882f1abbf.pdf?origin=publication_list |
| [16] | Lamperti G, Zanella M. Monitoring of active systems with stratified uncertain observations. IEEE Trans. on Systems, Man, and Cybernetics—Part A: Systems and Humans, . [doi:10.1109/TSMCA.2010.2069096] |
| [4] | 韩旭, 史忠植, 林芬. 基于模型诊断的研究进展. 高技术通讯, 2009, 19(5): 543–550. [doi:10.3772/j.issn.1002-0470.2009.05.018] |
| [5] | 赵相福, 欧阳丹彤. 离散事件系统基于模型诊断的研究进展. 计算机科学与探索, 2011, 5(2): 114–127. http://www.cnki.com.cn/Article/CJFDTOTAL-KXTS201102004.htm |
| [6] | 王晓宇, 欧阳丹彤, 赵相福. 不完备离散事件系统的可诊断性. 软件学报, 2015, 26(6): 1373–1385. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4585&journal_id=jos [doi:10.13328/j.cnki.jos.004585] |
| [9] | 王晓宇, 欧阳丹彤, 赵剑. 不完备模型下的离散事件系统诊断方法. 软件学报, 2012, 23(3): 465–475. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4028&journal_id=jos [doi:10.3724/SP.J.1001.2012.04028] |
 2017, Vol. 28
2017, Vol. 28


