2. 深圳大学 计算机与软件学院, 广东 深圳 518060;
3. 河北师范大学 数学与信息科学学院, 河北 石家庄 050024;
4. 河北师范大学 软件学院, 河北 石家庄 050024
2. College of Computer Science and Software Engineering, Shenzhen University, Shenzhen 518060, China;
3. College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang 050024, China;
4. Software College, Hebei Normal University, Shijiazhuang 050024, China
背包问题(knapsack problem, 简称KP)[1]是计算机科学中的一类重要的NPC问题, 也是一类经典的组合优化问题, 在投资决策与资源分配等方面具有重要的应用背景[2, 3].0-1背包问题(0-1 knapsack problem, 简称0-1KP)[2]是最典型的KP问题, 其一般描述为:从n个具有价值与重量的物品中选择若干个装入一个具有载重限制的背包, 如何选择物品使得装入物品的重量之和在不超过背包载重前提下价值之和达到最大.
设第i(1≤i≤n)个物品的价值与重量分别为vi与wi, 背包载重为C, 其中, vi, wi与C均为正整数; 令Y=(y1, y2, …, yn)∈{0, 1}n表示0-1KP的一个可行解, 当第i个物品被装入背包时yi=1, 否则yi=0, 则0-1KP的数学模型为:
| $ \max f(Y) = \max \sum\nolimits_{i = 1}^n {{v_i}{y_i}} $ | (1) |
| $ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&{\sum\nolimits_{i = 1}^n {{w_i}{y_i} \le C} } \end{array} $ | (2) |
动态背包问题(dynamic knapsack problem, 简称DKP)[4, 5]是0-1KP的一种动态扩展形式.在DKP中, 物品的价值、重量或背包载重不再固定不变, 而是随着时间的推移可能变大或缩小, 因此DKP是一种比0-1KP更不易求解的动态组合优化问题.
Goldberg等人[4]首先提出了背包载重在两个固定值之间振荡变化的DKP:时变背包问题(time-varying knapsack problem, 简称TVKP), 并且他们利用二倍体遗传算法(genetic algorithm, 简称GA)求解TVKP问题.随后, Hadad等人[6]改进了Goldberg等人的方法, 提出了求解TVKP的多倍体GA, 并指出其对于变化频率较大的TVKP多倍体方法更具有优势.Yang[7]利用原对偶遗传算法(primal-dual genetic algorithm, 简称PDGA)求解TVKP问题, 计算结果表明其求解效果优于基本GA.Lewis等人[8]比较了几种多倍体方法在求解TVKP时的优劣, 指出当背包载重在k(k≥3)个固定值之间振荡变化时多倍体方法的优势并不非常明显.周传华等人[9]提出了一种带动态小生境的自组织学习算法(DNSLA), 并将DNSLA用于求解多个规模为100的TVKP实例.贺毅朝等人[10, 11]利用动态规划(dynamic programming, 简称DP)求解背包载重在给定区间内随机振荡变化的TVKP问题, 提出了求解它的两种精确算法.李宁等人[12]则利用具有混合编码的和声搜索算法求解背包载重在给定区间内随机振荡变化的TVKP问题.
He等人[13]将TVKP推广为随机时变背包问题(randomized time-varying knapsack problem, 简称RTVKP), 并分别利用DP、贪心算法和GA给出了求解RTVKP问题的精确算法、近似算法和进化算法, 初步讨论了求解动态组合优化问题的近似算法优劣的评价标准.由于0-1KP是RTVKP的特例, 因此RTVKP也是一个NPC问题.此外, 随着时间的推移, RTVKP中物品的价值、重量以及背包载重均可能变大或减小, 故而RTVKP是比TVKP的求解难度更大的DKP.在本文中, 首先利用DP提出一种求解RTVKP的新精确算法, 然后分别基于差分演化和粒子群优化给出求解RTVKP的两种有效进化算法.
本文第1节给出RTVKP的定义与数学模型, 并简要分析其特性.第2节介绍利用第二动态规划法求解0-1KP的基本算法, 利用它们提出一种求解RTVKP的精确算法, 并比较其与已有精确算法的时间复杂度.第3节首先给出基于进化算法求解RTVKP时处理不可行解的有效算法GOA[13], 然后分别利用差分演化和粒子群优化与GOA相结合, 提出求解RTVKP问题的两种进化算法.第4节通过对5个较大规模RTVKP实例的仿真计算, 验证进化算法求解RTVKP问题的高效性与实用性.最后, 总结全文, 并提出今后进一步的研究思路.
1 RTVKP问题及其数学模型所谓随机时变背包问题(RTVKP)[13], 即给定n个物品和一个背包, 每个物品均具有价值与重量两种属性, 背包具有载重限制, 并且物品的价值和重量以及背包载重均可以随着时间的推移而动态随机振荡变化.如何在每一变化间隔周期内选择物品装入背包, 使得在不超过背包当前载重的前提下装入物品的价值之和达到最大.
设RTVKP中n个物品的初始价值集与初始重量集分别为V0={v01, v02, …, v0n}和W0={w01, w02, …, w0n}, v0j∈[Av, Bv], w0j∈[Aw, Bw](1≤j≤n), 背包初始载重为C0∈[Ac, Bc], 其中Av, Bv, Aw, Bw, Ac和Bc均为正整数, 且Av < Bv, Aw < Bw, Bw < Ac < Bc < nAw.令Ti(i≥1)表示物品的价值、重量或背包载重的第i-1次随机振荡变化与第i次随机振荡变化之间的时间间隔(即在此间隔内物品的价值、重量和背包载重都是固定不变的), 称为第i次随机变化周期(单位为s).记第i(i≥1)次随机变化后n个物品的价值集与重量集分别为Vi={vi1, vi2, …, vin}和Wi={wi1, wi2, …, win}, 背包载重为Ci∈[Ac, Bc], 其中vij∈[Av, Bv], wij∈[Aw, Bw](1≤j≤n), 并且满足|(Vi∪Wi)-(Vi-1∪Wi-1)|≤Threshold(一般取
令Yi=(yi1, yi2, …, yin)∈{0, 1}n表示RTVKPi(i≥0)的可行解, 则此时第j(1≤j≤n)个物品装入载重为Ci的背包时yij=1, 否则yij=0.于是, 在Ti+1的时间限制下, RTVKP的数学模型描述如下:
| $ \max f({Y_i}) = \max \sum\nolimits_{j = 1}^n {{y_{ij}}{v_{ij}}} $ | (3) |
| $ \begin{array}{*{20}{c}} {{\rm{s}}{\rm{.t}}{\rm{.}}}&{\sum\nolimits_{j = 1}^n {{y_{ij}}{w_{ij}} \le {C_i}} } \end{array} $ | (4) |
其中, i≥0, 1≤j≤n; Vi={vi1, vi2, …, vin}和Wi={wi1, wi2, …, win}分别为RTVKPi对应的价值集和重量集, Ci为背包载重.
当RTVKP的物品价值集和重量集均不发生变化时, 即(Vi∪Wi)-(Vi-1∪Wi-1)=∅时, RTVKP退化为TVKP.显然, RTVKP是由一系列具有部分共同数据的0-1KP子问题构成的, 即子问题RTVKPi与RTVKPi+1(i≥0)的大部分物品的价值与重量是相同的, 只有少部分物品的价值、重量或背包载重是相异的.正是由于RTVKP的子问题之间的这种共有数据特征, 使得能够利用DP对其进行求解.
令MinT=min{Ti|Ti为RTVKP的第i次随机变化周期, i≥1}, 则RTVKP实例的MinT值越小, 要求算法适应其振荡变化的能力就越高, 实例就越不容易被成功求解.此外, 当RTVKP问题的随机变化周期Ti恒为常数时, 称其为具有固定变化周期的RTVKP, 并简记为fixRTVKP.
2 基于动态规划法求解RTVKP问题动态规划(DP)[11, 14-16]是一种重要的算法设计方法, 适于求解具有最优子结构性质的最优化问题.在利用DP求解问题时, 刻画子问题的最优解的结构特征, 并依此建立问题与子问题最优值之间的递推公式是算法设计的关键所在; 一旦建立了递推公式, 就可以根据它按照自底向上的方式逐一求解各子问题的最优值, 最终求得原问题的最优值(这一过程通常利用填表实现); 然后, 根据求得的最优值和递推公式, 按照自顶向下的方式逐步确定问题的一个最优解(这一过程通常是按照与填表相反的顺序查表实现).
下面首先给出求解0-1KP的第二动态规划法[11, 16], 然后利用它提出一种求解RTVKP问题的具有伪多项式时间的新精确算法.
设0-1KP问题的价值集与重量集分别为V={v1, v2, …, vn}和W={w1, w2, …, wn}, 背包载重为C.为了建立0-1KP最优值的递推公式, 令Uik表示从前i个物品中选择物品装入背包, 当所选择物品的价值之和等于k时重量之和所能达到的最小值, 其中, 1≤i≤n, 0≤k≤P且
| $ {U_{ik}} = \left\{ {\begin{array}{*{20}{l}} {\min \{ {U_{i - 1,k}},{U_{i - 1,k - {v_i}}} + {w_i}\} ,}&{{\rm{if }}{v_i} \le k,{\rm{ }}i \ge 2}\\ {{U_{i - 1,k}},}&{{\rm{if }}{v_i} > k,{\rm{ }}i \ge 2} \end{array}} \right. $ | (5) |
初始条件为Ui0=0(1≤i≤n), U1k=∞(1≤k≤P, k≠v1)且
设Uik(1≤i≤n, 0≤k≤P)存于二维数组U[1…n, 0…P]中, 其中
算法1. OPTfor0-1KP.
输入:集合V和W; 参数C, T, n, low, high, P0和P.
输出:二维数组U[low...high, P0…P].
1. time←SystemTime();
2. if P0=0 then
3. fori=low to high do U[i, 0]←0;
4. end if
5. if low=1 then
6. for k=1 to P do U[1, k]←∞;
7. U[1, v1]←w1;
8. end if
9. for i=low to high do
10. for k=P0 to P do
11. U[i, k]←U[i-1, k];
12. if vi≤k then
13. if SystemTime()-time≥T and (k < P or i < high) then return (“Solving failure”);
14. end for
15. end for
16. return (U[low...high, P0…P]).
算法1的时间复杂度为O((high-low+1)(P-P0+1)).注意到, 当P > > P0时, P-P0+1是一个大整数, log2(P-P0+1)为其输入规模, 因此算法1是一种伪多项式时间精确算法.在求0-1KP时, 首先利用算法1计算U[1…n, 0…P], 其调用方式为OPTfor0-1KP(n, V, W, C, 1, n, 0, P, T), 然后由
在算法1的基础上, 求解0-1KP最优解的算法SOLfor0-1KP描述如下.
算法2. SOLfor0-1KP.
输入:集合V和W; 参数n, C, OPT; 二维数组U[1…n, 0…P].
输出:0-1KP问题的最优解Y=(y1, y2, …, yn)∈{0, 1}n.
1. i←n; k←OPT;
2. for i=1 to n do yi←0;
3. while (i > 1 and k > 0) do
4. if U[i, k]=U[i-1, k-vi]+wi then yi←1 and k←k-vi;
5. i←i-1;
6. end while
7. if (i=1 and U[1, k]=w1) then y1←1;
8. return (Y).
算法2输出0-1KP的一个最优解Y, 其算法时间复杂度为Θ(n); 在算法2的输入参数中, OPT是最优解Y对应的最优值.对于0-1KP, 利用算法2求其最优解的调用方式为SOLfor0-1KP(n, V, W, C, OPT, U[1…n, 0…P]).
下面首先利用算法1和算法2基于动态规划法阐述求解RTVKP问题的算法(记为DPfRTVKP)设计思想, 然后给出其算法伪代码描述.
初始时, 调用算法1和算法2在随机变化周期T1内直接求解子问题RTVKP0(n, C0, V0, W0).
假设子问题RTVKPi(n, Ci, Vi, Wi)(i≥0)已经求解完毕, 并且其某些物品的价值和重量或背包载重发生变化得到后继子问题RTVKPi+1(n, Ci+1, Vi+1, Wi+1), 则按照如下的两种情形对RTVKPi+1进行求解.
(1) 当(Vi+1∪Wi+1)-(Vi∪Wi)=∅时, 说明RTVKPi随机变化为RTVKPi+1时仅有背包载重发生了改变, 物品的价值与重量均未改变, 此时直接利用
(2) 当(Vi+1∪Wi+1)-(Vi∪Wi)≠∅时, 说明RTVKPi随机变化为RTVKPi+1时至少有1个物品的价值或重量发生了改变, 于是令
(2.1) 如果Pi≥Pi+1, 则求解RTVKPi时已经计算的Uik(1≤i≤low-1, 0≤k≤Pi+1)对于RTVKPi+1仍适用, 此时只需利用算法1重新计算Uik(low≤i≤n, 0≤k≤Pi+1)即可;
(2.2) 如果Pi < Pi+1, 则求解RTVKPi时已经计算的Uik(1≤i≤low-1, 0≤k≤Pi)对于RTVKPi+1仍适用, 此时只需利用算法1分别计算Uik(1≤i≤low-1, Pi+1≤k≤Pi+1)和Uik(low≤i≤n, 1≤k≤Pi+1)即可.
在按照上述方法计算出Uik(1≤i≤n, 0≤k≤Pi+1)之后, 利用
令m为RTVKP的随机振荡变化次数, 则RTVKP可视为由m个0-1KP子问题构成.令V={v1, v2, …, vn}与W={w1, w2, …, wn}分别表示子问题的价值集和重量集, C表示背包载重.设函数CheckVary(V0, W0, C0)的作用是在V0, W0和C0的基础上, 在区间[Av, Bv], [Aw, Bw]和[Ac, Bc]上随机产生新的价值集V、重量集W和背包载重C, 函数GetPeriod()用于产生新的随机变化周期T, 函数FindIndex((V∪W)-(V0∪W0))用于确定集合(V∪W)-(V0∪W0)中物品的最小下标, 于是DPfRTVKP的算法伪代码描述如下.
算法3. DPfRTVKP.
输入:初始价值集V0={v01, v02, …, v0n}; 初始重量集W0={w01, w02, …, w0n}; 初始背包载重C0; 参数n, m, Threshold, Av, Bv, Aw, Bw, Ac和Bc.
输出:RTVKP的m个子问题的最优值与最优解.
1. V←V0; W←W0; C←C0;
2. P0←0;
3. T←GetPeriod(); time←SystemTime();
4. (U[low...high, P0…P])←OPTfor0-1KP(n, V, W, C, low, high, P0, P, T);
5. while (k < m) do
6. if (V∪W)-(V0∪W0)≠∅ then
7. if P0 < P then
8. (U[1...low-1, P0+1…P])←OPTfor0-1KP(n, V, W, C, 1, low-1, P0+1, P, T);
9. T←T-SystemTime()+time;
10. end if
11. (U[low...n, 0…P])←OPTfor0-1KP(n, V, W, C, low, n, 0, P, T);
12. endif
13.
14. Y←SOLfor0-1KP(n, V, W, C, OPT, U[1…n, 0, …P]);
15. return (OPT, Y);
16. while (SystemTime()-time < T) do SystemTime();
17. if (k < m-1) then
18. V0←V; W0←W; C0←C; P0←P; T←GetPeriod();
19. (V, W, C)←CheckVary(V0, W0, C0);
20. low←FindIndex((V∪W)-(V0∪W0)); time←SystemTime();
21. end if
22. k←k+1;
23. end while
24. return (“Success to solve”).
注意到RTVKP的规模由物品个数n和子问题数m确定, 记Pmax=max ({|Pi-Pi-1||1≤i≤m-1}∪{P0}), 其中,
由于Pmax往往是一个大整数, log2Pmax为其输入规模, 所以算法3是一种具有伪多项式时间的精确算法.显然, O(nPi) < Ti+1(0≤i≤m-1)是保证DPfRTVKP能够成功求解RTVKP中每一个子问题的充分条件, 因此O(nPmax) < MinT是保证DPfRTVKP能够成功求解RTVKP问题的一个充分条件.
类似地, 令Cmax=max ({|Ci-Ci-1||1≤i≤m-1}∪{C0}), Ci(0≤i≤m-1)为RTVKPi的背包载重, 则算法DPMfRDKP[13]的时间复杂度为
比较DPfRTVKP与DPMfRDKP的时间复杂度以及成功求解RTVKP问题的充分条件易知:在保证算法能够成功求解RTVKP问题的前提下, 当O(nmPmax) < O(nmCmax)时, 算法DPfRTVKP的求解速度快; 当O(nmCmax) < O(nmPmax)时, 算法DPMfRDKP的求解速度快.于是有如下r结论.
结论1. 当Pmax < min{Ci|0≤i≤m-1}时, DPfRTVKP更适于求解RTVKP问题; 当Cmax < min{Pi|0≤i≤m-1}时, DPMfRDKP则更适于求解RTVKP问题.
3 基于进化算法求解RTVKP问题进化算法(evolutionary algorithm, 简称EA)[17, 18]是一类群智能启发式算法, 常见的有遗传算法(genetic algorithm, 简称GA)[18]、差分演化(differential evolution, 简称DE)[19-21]、蚁群优化(ant colony optimization, 简称ACO)[22]、粒子群优化(particle swarm optimization, 简称PSO)[23, 24]、混合蛙跳算法(shuffled frog-leaping algorithm, 简称SFLA)[25]与和声搜索算法(harmony search algorithm, 简称HSA)[12, 26]等.目前EAs已被广泛应用于求解各种组合优化问题, 如0-1KP问题、可满足性问题(satisfiability problem, 简称SAT)[27]和旅行商问题(traveling salesman problem, 简称TSP)[28]等, 其中利用GA, PSO, DE和HSA及其改进算法求解0-1KP和TVKP已被众多学者所研究[4, 6-9, 12, 21, 29, 30].在本节中, 我们首先给出利用EAs求解RTVKP实例时处理不可行解的一种有效方法, 然后借鉴文献[13]中的算法设计思想, 基于HBDE[21]和DS_BPSO[24]分别给出求解RTVKP的两种进化算法.
3.1 一种处理不可行解的有效方法RTVKP是一个约束优化问题, 在利用EAs求解时需要解决的一个关键问题是如何保证个体编码满足约束条件.通常将不满足约束条件的个体编码对应的解称为不可行解.对于约束优化问题, 处理不可行解的常见方法[31-33]有:罚函数法(penalty function approach)、修复法(repair approach)、纯正法(purist approach)、分离法(separatist approach)和混合方法(hybrid approach).罚函数法通过在目标函数中引入一个惩罚项, 将约束优化问题转化为非约束优化问题.修复法是一种将不可行解按照某种策略修正为可行解的处理方法.纯正法是在进化过程中通过拒绝对应不可行解的个体来满足约束条件.分离法是一种将目标函数和约束条件分开进行处理的方法.混合法是指同时使用以上至少两种方法的综合处理方法.
对于一般的约束优化问题, 以上方法各有利弊; 但对于0-1KP, Michalewicz等人[33]经过研究指出修复法是最为适宜的, 并且基于贪心策略给出了一种修复不可行解的有效方法.注意到, RTVKP本质上是由一系列具有部分共同数据的0-1KP子问题构成, 因此在利用EAs求解时采用修复法处理不可行解是最佳选择.正是基于以上原因, He等人[13]利用修复法与遗传算法相结合求解RTVKP问题, 并在Michalewicz等人[33]所提出方法的基础上引入优化策略, 给出了一种效果更佳的修复方法:贪心优化算法(greedy optimization algorithm, 简称GOA)[13].下面我们给出GOA的伪代码描述.
设Y=(y1, y2, …, yn)∈{0, 1}n为EAs的某个体对应0-1KP实例的0-1解向量, 注意, 解向量Y不一定为0-1KP实例的可行解.令H[1…n]为一个二维数组, 用于存放利用快速排序算法(QuickSort)[14, 15]按照物品的价值与重量的比值大小对物品进行排序后物品的下标, 则GOA的算法伪代码描述如下.
算法4. GOA.
输入:0-1KP实例的维数n; 价值集V={v1, v2, …, vn}; 重量集W={w1, w2, …, wn}; 背包载重C; 个体Y=(y1, y2, …, yn); 二维数组H[1…n].
输出:修复与优化后的可行解Y=(y1, y2, …, yn)及其目标函数值f(Y).
1. fweight←0; fvalue←0;
2. for i=1 to n do fweight←fweight+yixwi;
3. if fweight > C then
4. temp←0;
5. for i=1 to n do
6. temp←temp+yH[i]xwH[i];
7. iftemp > C then temp←temp-yH[i]xwH[i] and yH[i]←0;
8. end for
9. fweight←temp;
10. end if
11. for i=1 to n do
12. if (yH[i]=0 and fweight+wH[i]≤C) then yH[i]←1 and fweight←fweight+wH[i];
13. end for
14. for i=1 to n do fvalue←fvalue+yixvi;
15. return (Y, fvalue);
在算法4中, 若个体Y是不可行解, 则Step 3~Step 10用于对其进行修正, 否则不起作用; Step 11~Step 13用于对可行解(包括修复后的可行解)做进一步的优化, Step 14则用于计算Y的目标函数值f(Y).最后, 算法输出优化后的可行解Y及其适应度值f(Y)=fvalue.显然, GOA的时间复杂度为Θ(n).
3.2 基于差分演化求解RTVKP问题差分演化(DE)[19, 20]是由Rainer Storn和Kenneth Price于1996年提出的一种具有极强全局搜索能力的EAs, 因其在第1届IEEE演化大赛中表现超群, 引起了国内外学者的极大关注.目前, DE已被广泛应用于求解许多领域中的数值优化问题和组合优化问题[19-21, 34-37].为了利用DE求解问题的解可表示为0-1向量的组合优化问题, 贺毅朝等人[21]提出了一种具有混合编码的二进制差分演化算法(HBDE), 并利用它求解0-1KP和SAT问题.下面首先基于最大优化问题简介HBDE的基本原理, 然后将其与GOA相结合, 提出一种求解RTVKP问题的进化算法.
记P(t)为HBDE的第t(t≥0)代种群, 其第i个个体的混合编码为(Xi(t), Yi(t)), 其中Xi(t)=(xi1(t), xi2(t), …, xin(t))∈
| $ {z_{ij}}(t) = \left\{ {\begin{array}{*{20}{l}} {{x_{{p_1}j}}(t) + \alpha (x{}_{{p_2}j}(t) - {x_{{p_3}j}}(t)),}&{{\rm{if }}r \le CR{\rm{ or }}j = R(i)}\\ {{x_{ij}}(t),}&{{\rm{otherwise}}} \end{array}} \right. $ | (6) |
| $ {e_{ij}}(t) = \left\{ {\begin{array}{*{20}{l}} {1,}&{sig({z_{ij}}(t)) \ge 0.5}\\ {0,}&{{\rm{otherwise}}} \end{array}} \right. $ | (7) |
其中, 1≤i≤N, 1≤j≤n; (Xp1(t), Yp1(t)), (Xp2(t), Yp2(t)), (Xp3(t), Yp3(t))分别是P(t)中3种不同于(Xi(t), Yi(t))的不同个体. 0 < a < 1称为缩放因子, CR∈(0, 1)称为变异因子, r是(0, 1)上的一个随机实数, R(i)是[1, n]上的一个随机正整数, sig(x)=1/(1+e-x)是模糊函数.
在HBDE的差异算子中, 混合编码个体(X(t), Y(t))的第2个分量Y(t)并不参与产生中间个体(Z(t), E(t))的计算, 而是用于表示第1个分量X(t)对应于问题的潜在解.显然, 这种编码方法可以使HBDE保持DE原有的进化方式, 从而继承DE的全局搜索能力.
HBDE的选择算子是一种贪心选择算子, 即如果中间种群Q(t)中个体(Zi(t), Ei(t))优于种群P(t)中的个体(Xi(t), Yi(t)), 则选择(Zi(t), Ei(t))作为第t+1代种群P(t+1)中的第i个个体(Xi(t+1), Yi(t+1)), 否则选择(Xi(t), Yi(t)), 即
| $ ({X_i}(t + 1),{Y_i}(t + 1)) = \left\{ \begin{array}{l} ({Z_i}(t),{E_i}(t))\begin{array}{*{20}{c}} ,&{\begin{array}{*{20}{c}} {{\rm{if}}} \end{array}f({E_i}(t)) > f({Y_i}(t))} \end{array}\\ ({X_i}(t),{Y_i}(t))\begin{array}{*{20}{c}} ,&{{\rm{othewise}}} \end{array} \end{array} \right. $ | (8) |
其中, 1≤i≤N, f(Y)为Y对应的目标函数值(一般可作为个体(X, Y)的适应度).
对于最大优化问题, 记P(t)中最优个体(U(t), B(t))为适应度最大的个体, 即(U(t), B(t))是P(t)中满足f(B(t))≤f(Yi(t))(1≤i≤N)的个体.由于选择算子是贪心方式的, 因此(U(t), B(t))必为HBDE前t代进化获得的全局最优个体.
令m为RTVKP的随机振荡变化次数, V={v1, v2, …, vn}与W={w1, w2, …, wn}分别为子问题的价值集和重量集, C为背包载重.记“H[1…n]←QuickSort({vi/wi|vi∈V, wi∈W, 1≤i≤n})”表示利用快速排序算法(QuickSort)[14, 15]按照物品价值与重量的比值对物品进行排序后将物品下标依次存储于数组H[1…n]中.函数SystemTime(), CheckVary(V, W, C), GetPeriod()和FindIndex((V∪W)-(V0∪W0))和T的含义同上, 于是利用HBDE与GOA相结合求解RTVKP的进化算法(记为HBDEfRTVKP)的伪代码描述如下.
算法5. HBDEfRTVKP.
输入:初始价值集V0={v01, v02, …, v0n}; 初始重量集W0={w01, w02, …, w0n}; 初始背包载重C0; 参数n, m, Threshold, Av, Bv, Aw, Bw, Ac和Bc; 种群规模N, Lj和Uj(1≤j≤n).
输出:RTVKP的m个子问题的最优值和最优解.
1. V←V0; W←W0; C←C0; k←0;
2. T←GetPeriod(); time←SystemTime();
3. while (k < m) do
4. Generate the initial population P(0)={(Xi(0), Yi(0))|1≤i≤N} randomly;
5. t←0;
6. H[1…n]←QuickSort({vi/wi|vi∈V, wi∈W, 1≤i≤n});
7. for i=1 to N do (Yi(t), f(Yi(t)))←GOA(n, V, W, C, Yi(t), H[1…n]);
8. Get (U(t), B(t)) from P(t) according to f(Yi(t)) (1≤i≤N);
9. while (SystemTime()-time < T) do
10. for i=1 to N do
11. for j=1 to n do
12. if (≤CR∨j=R(i))then zij←yp1, j+a(yp2, j-yp3, j) else zij←yij;
13. if sig(zij)≥0.5 then eij←1 else eij←0;
14. endfor
15. if(SystemTime()-time≥T) then goto 23;
16. (Ei(t), f(Ei(t)))←GOA(n, V, W, C, Ei(t), H[1…n]);
17. if f(Ei(t) > f(Yi(t)) then (Xi(t+1), Yi(t+1))←(Zi(t), Ei(t));
18. else (Xi(t+1), Yi(t+1))←(Xi(t), Yi(t));
19. endfor
20. t←t+1;
21. Get (U(t), B(t)) from P(t) according to f(Yi(t)) (1≤i≤N);
22. endwhile
23. output (f(B(t)), B(t));
24. if (k < m-1) then
25. V0←V; W0←W; C0←C; T←GetPeriod();
26. (V, W, C)←CheckVary(V0, W0, C0); time←SystemTime();
27. end if
28. k←k+1;
29. end while
30. return(“Success to solve”).
由于算法5是一种随机近似算法, 只要时间允许它将一直保持进化搜索.因此, 在RTVKP的每个随机变化周期内, 算法5将一直保持求解状态, 讨论其时间复杂度是没有意义的, 故而下面重点分析它能够求得RTVKP问题的一个较好近似解应该满足的条件.注意到算法5中Step 4和Step 7的时间复杂度均为Θ(nN), Step 6的时间复杂度为Θ(nlogn), Step 8的时间复杂度为Θ(n+N), 而对于RTVKP的每一个子问题, 只要算法5能够产生至少1代种群(即执行完Step 4~Step 8), 即可由当前最优个体给出子问题的一个近似解, 因此保证HBDEfRTVKP能够求得RTVKP实例的一个近似解的充分条件是Θ(n(N+logn)) < MinT.
事实上, 充分条件Θ(n(N+logn)) < MinT虽然能够保证HBDEfRTVKP求得RTVKP问题的近似解, 但是这个近似解的近似程度却是难以确定的.一般地, 进化算法的迭代进化次数越多, 求得问题的近似解越好, 甚至可能求得最优解.由于通常总有N < < n, 因此HBDEfRTVKP求解RTVKP的各子问题时, 一次迭代进化的时间复杂度上界为O(n2), 其迭代进化一次的时间非常短, 所以在求解各子问题时总能够迭代多次, 从而求得较好的近似解或最优解.这一点将在第4节的实例计算中得到验证.
3.3 基于粒子群优化求解RTVKP问题粒子群优化(PSO)[23]是由Kennedy和Eberhart提出的一种仿生进化算法, 也是目前应用范围最广的进化算法之一[23, 24, 38-42].标准PSO仅适用于求解连续域上的最优化问题, 为了能够求解离散域上的最优化问题, Kennedy等人[42]首先提出了一种二进制粒子群优化算法(binary particle swarm optimization, 简称BPSO), 但是BPSO在求解某些组合优化问题(如SAT问题)时效果并不理想.贺毅朝等人通过采用双重编码结构(其实质与HBDE的混合编码思想相同), 在BPSO的基础上提出了一种改进的二进制粒子群优化算法:具有双重结构编码的二进制粒子群优化算法(DS_BPSO)[24], DS_BPSO弥补了BPSO的种群多样性差和全局搜索能力相对低下的缺陷, 在求解0-1KP、随机3-SAT问题和TVKP时表现突出[24, 30].
下面首先基于最大优化问题简述DS_BPSO的基本原理, 然后给出它与GOA相结合求解RTVKP的进化算法的伪代码描述.
在DS_BPSO的第t代种群P(t)中, 第i个粒子(即第i个个体)用有序三元组((Xi(t), Yi(t)), Vi(t))表示, 其中, 1≤i≤N, N为种群规模, Xi(t)=(xi1(t), xi2(t), …, xin(t))与Vi(t)=(vi1(t), vi2(t), …, vin(t))分别为粒子的位置与速度, 并且Xi(t), Vi(t)∈
记(Zi(t), Bi(t))为P(t)中第i个粒子的历史最好位置及其对应的二进制解向量, 其中, Zi(t)=(zi1(t), zi2(t), …, zn(t))∈
记(Zg(t), Bg(t))为DS_BPSO在前t代迭代中求得的全局最好位置及其对应的二进制解向量, 即(Zg(t), Bg(t))∈ {(Zi(t), Bi(t))|1≤i≤N}且f(Bg(t))=max{f(Bi(t))|1≤i≤N}, 则由P(t)中第i个粒子((Xi(t), Yi(t)), Vi(t))产生种群P(t+1)中第i个粒子((Xi(t+1), Yi(t+1)), Vi(t+1))的计算公式由式(9)~式(11)给出.
| $ {v_{ij}}\left( {t + 1} \right) = {v_{ij}}\left( t \right) + {c_1}{r_1}\left( {{z_{ij}}\left( t \right)-{x_{ij}}\left( t \right)} \right) + {c_2}{r_2}\left( {{z_{gj}}\left( t \right)-{x_{ij}}\left( t \right)} \right) $ | (9) |
| $ {x_{ij}}(t + 1) = {x_{ij}}(t) + {v_{ij}}(t + 1) $ | (10) |
| $ {y_{ij}}(t + 1) = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{if}}\;sig({x_{ij}}(t + 1)) \ge 0.5}\\ {0,}&{{\rm{otherwise}}} \end{array}} \right. $ | (11) |
其中, 1≤i≤N, 1≤j≤n; r1和r2分别是(0, 1)中两个独立的随机实数, c1和c2称为加速常数, 一般均在0~2之间取值; sig(x)=1/(1+e-x)是模糊函数.
于是, 利用第4.2节中的相关约定和表示, 基于DS_BPSO与GOA相结合求解RTVKP问题的进化算法(记为DPSOfRTVKP)的伪代码描述如下.
算法6. DPSOfRTVKP.
输入:初始价值集V0={v01, v02, …, v0n}; 初始重量集W0={w01, w02, …, w0n}; 初始背包载重C0; 参数n, m, Threshold, Av, Bv, Aw, Bw, Ac和Bc; 种群规模N, Lj和Uj(1≤j≤n).
输出:RTVKP的m个子问题的最优值和最优解.
1. V←V0; W←W0; C←C0; k←0;
2. T←GetPeriod(); time←SystemTime();
3. while (k < m) do
4. Generate the initial population P(0)={((Xi(0), Yi(0)), Vi(0))|1≤i≤N} randomly;
5. H[1…n]←QuickSort({vi/wi|vi∈V, wi∈W, 1≤i≤n});
6. for i=1 to N do(Yi(0), f(Yi(0)))←GOA(n, V, W, C, Yi(0), H[1…n]);
7. for i=1 to N do(Zi(0), Bi(0))←(Xi(0), Yi(0)); t←0;
8. Get (Zg(t), Bg(t)) from {(Zi(t), Bi(t))|1≤i≤N} according to f(Bi(t));
9. while (SystemTime()-time < T) do
10. for i=1 to N do
11. for j=1 to n do
12. vij(t+1)←vij(t)+c1r1(zij(t)-xij(t))+c2r2(zgj(t)-xij(t));
13. xij(t+1)←xij(t)+vij(t+1);
14. if sig (xij(t+1))≥0.5then yij(t+1)←1 else yij(t+1)←0;
15. endfor
16. if(SystemTime()-time≥T) then goto 24;
17. (Yi(t+1), f(Yi(t+1)))←GOA(n, V, W, C, Yi(t+1), H[1…n]);
18. if f(Yi(t+1))≥f(Bi(t))then (Zi(t+1), Bi(t+1))←(Xi(t+1), Yi(t+1));
19. else (Zi(t+1), Bi(t+1))←(Zi(t), Bi(t));
20. endfor
21. t←t+1;
22. Get (Zg(t), Bg(t)) from {(Zi(t), Bi(t))|1≤i≤N} according to f(Bi(t));
23. endwhile
24. output(f(Bg(t)), Bg(t));
25. if (k < m-1) then
26. V0←V; W0←W; C0←C; T←GetPeriod();
27. (V, W, C)←CheckVary(V0, W0, C0); time←SystemTime();
28. end if
29. k←k+1;
30. end while
31. return(“Success to solve”).
算法6也是一种随机近似算法, 利用它求解RTVKP问题时, 能否保证算法得到一个较为满意的近似解仍是算法的关键.注意到算法6中Step 4, Step 6和Step 7的时间复杂度均为Θ(nN), Step 5的时间复杂度为Θ(nlogn), Step 8的时间复杂度为Θ(n+N), 而对于RTVKP的每一个子问题, 只要DPSOfRTVKP能够产生至少1代种群(即执行完Step 4~Step 8)即可由当前最优个体给出问题的一个近似解, 所以保证DPSOfRTVKP能够求得RTVKP的近似解的充分条件与HBDEfRTVKP的相同, 也为Θ(n(N+logn)) < MinT.同样地, 利用DPSOfRTVKP求解RTVKP的子问题时, 一次迭代进化的时间复杂度的上界为O(n2), 因此其迭代进化一次的时间是非常短的, 从而在求解RTVKP的各子问题时总能够较快地求得更好的近似解, 甚至可能是最优解.
4 实例计算与比较由于HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP[13]均为随机近似算法, 比较其时间复杂度是没有意义的.因此, 为了说明它们的高效性和实用性, 下面利用文献[13]中的fixRTVKP实例1~实例3以及fitRTVKP实例4和实例5(其具体数据见http://pan.baidu.com/s/1BDgn0)进行计算, 并与DPfRTVKP和GAAfRDKP[13]的计算结果进行比较.所有仿真计算使用微型计算机DELL Intel (R) Pentium (R)4-CPU 1.69GHz, 内存为256M, 操作系统为MicroSoft Windows XP.利用Visual C++ 6.0进行编程, 利用MATLAB 7.1绘制算法的平均收敛曲线.
3种进化算法的种群规模N均为50.在HBDEfRTVKP中, a=0.5, CR=0.3;在DPSOfRTVKP中, c1=c2=2.0;并且在HBDEfRTVKP和DPSOfRTVKP中均取Lj=-5.0, Uj=5.0(1≤j≤n).EGAfRDKP的参数取值参见文献[13].
在表 1~表 5中, 给出了利用HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP对实例1~实例5的20次求解得到的最好值(即各子实例的最好值序列, 用Best表示)、最差值(用Worst表示)、最好值在20次计算中出现的比例(用Rate表示)和20次计算结果的平均值(用Mean表示), 并将以上结果与利用精确算法DPfRTVKP得到的最优值(用Optimal表示)和近似算法GAAfRDKP得到的近似值(用Approx表示)进行比较.
| Table 1 Comparing results of HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP for solving Instance 1 表 1 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例1的结果比较 |
| Table 2 Comparing results of HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP for solving Instance 2 表 2 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例2的结果比较 |
| Table 3 Comparing results of HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP for solving Instance 3 表 3 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例3的结果比较 |
| Table 4 Comparing results of HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP for solving Instance 4 表 4 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例4的结果比较 |
| Table 5 Comparing results of HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP for solving Instance 5 表 5 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例5的结果比较 |
从表 1中的计算结果可看出, HBDEfRTVKP以100%的概率求得实例1的最优值.DPSOfRTVKP以100%求得子实例RTVKP0~RTVKP8的最优值, 虽然不能求得最后一个子实例的最优值, 但其求得的最好值与最优值之间相差仅为1.EGAfRTVKP除了子实例RTVKP5, RTVKP8和RTVKP9以外, 以100%的概率求得其余子实例的最优值, 即使对于子实例RTVKP5, RTVKP8和RTVKP9, 它求得的最好值与最优值之间的差值也是极小的.显然, HBDEfRTVKP是3种进化算法中求解效果最佳的, DPSOfRTVKP和EGAfRTVKP的求解效果次之, 而且3种进化算法求得的最差值均明显优于GGAfRDKP.
从表 2中的计算结果可以看出, HBDEfRTVKP以100%的概率求得子实例RTVKP0, RTVKP3, RTVKP5~RTVKP8的最优值, 以至少20%的概率求得子实例RTVKP2, RTVKP4和RTVKP9的最优值, 但对子实例RTVKP1, 它所求得的最好值与最优值仅相差22.DPSOfRTVKP以100%的概率求得子实例RTVKP3的最优值, 以至少40%的概率求得子实例RTVKP0~RTVKP2, RTVKP4, RTVKP6~RTVKP8的最优值, 虽然不能求得子实例RTVKP5和RTVKP9的最优值, 但其得到的最好值与最优值之间的差值仅为1和6.EGAfRTVKP以100%的概率求得子实例RTVKP2和RTVKP6的最优值, 以至少20%的概率求得子实例RTVKP0, RTVKP1, RTVKP3, RTVKP4, RTVKP7和RTVKP8的最优值, 虽然不能得到子实例RTVKP5和RTVKP9的最优值, 但求得的最好值与最优值之间的差值仅为1和3.显然, HBDEfRTVKP求得实例2的最好值略优于DPSOfRTVKP和EGAfRTVKP, 但是它们求得的平均值相差不大, 且它们求得的最差值也均优于GGAfRDKP.
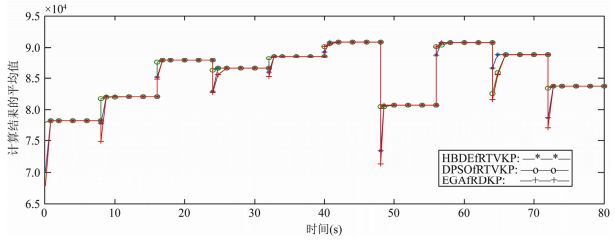
从表 3中的计算结果可看出:HBDEfRTVKP以100%的概率求得子实例RTVKP0, RTVKP1, RTVKP3~RTVKP6, RTVKP8和RTVKP9的最优值, 以至少25%的概率求得子实例RTVKP2的最优值, 虽然不能求得子实例RTVKP7的最优值, 但所得最好值与最优值仅相差1.DPSOfRTVKP以100%的概率求得子实例RTVKP1, RTVKP3, RTVKP5和RTVKP8的最优值, 以至少20%的概率求得子实例RTVKP0, RTVKP4, RTVKP6和RTVKP9的最优值, 虽然不能求得子实例RTVKP2和RTVKP7的最优值, 但得到的最好值与最优值之间的差值也是很小的.EGAfRTVKP以100%的概率求得子实例RTVKP0, RTVKP3, RTVKP5和RTVKP8的最优值, 以至少10%的概率求得子实例RTVKP1, RTVKP2, RTVKP4, RTVKP6和RTVKP9的最优值, 即使对于子实例RTVKP7, 求得的最好值与最优值之间的差值也是很小的.显然, HBDEfRTVKP, DPSOfRTVKP和EGAfRTVKP求解实例3的效果与求解实例2时是相同的.
从表 4中的计算结果可以看出, HBDEfRTVKP以100%的概率求得子实例RTVKP0, RTVKP3, RTVKP5, RTVKP6和RTVKP8的最优值, 以至少50%的概率求得子实例RTVKP2和RTVKP4的最优值, 虽然不能求得子实例RTVKP1, RTVKP7和RTVKP9的最优值, 但所得最好值与最优值之间最多仅相差10. DPSOfRTVKP以100%的概率求得子实例RTVKP0, RTVKP3, RTVKP5和RRTVKP8的最优值, 以60%的概率求得子实例RTVKP6的最优值; 虽然不能求得子实例RTVKP1, RTVKP2, RTVKP4, RTVKP7和RTVKP9的最优值, 但其得到的最好值与最优值之间的差值最多也仅相差10.EGAfRTVKP以100%的概率求得子实例RTVKP0, RTVKP3, RTVKP5和RTVKP6的最优值, 虽然不能得到子实例RTVKP1, RTVKP2, RTVKP4, RTVKP7, RTVKP8和RTVKP9的最优值, 但求得的最好值与最优值之间的差值最多仅为8.显然, 3种进化算法求解实例4的效果基本相同, 且它们求得的最差值均优于GAAfRDKP.
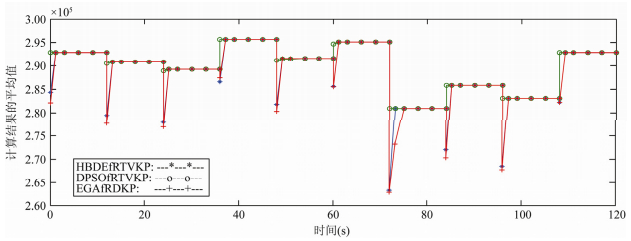
从表 5中的计算结果可以看出, HBDEfRTVKP以100%的概率求得子实例RTVKP0~RTVKP8的最优值, 以60%的概率求得子实例RTVKP9的最优值, 求解效果非常好.DPSOfRTVKP以100%的概率求得子实例RTVKP0, RTVKP6和RRTVKP8的最优值, 以至少20%的概率求得子实例RTVKP1~RTVKP5和RTVKP7的最优值, 虽然不能求得子实例RTVKP9的最优值, 但其得到的最好值与最优值之间的差值仅为7.EGAfRTVKP以100%的概率求得子实例RTVKP2~RTVKP4, RTVKP6~RTVKP8的最优值, 以90%的概率求得子实例RTVKP1的最优值, 虽然不能得到子实例RTVKP0, RTVKP5和RTVKP9的最优值, 但求得的最好值与最优值之间的差值最多仅为7.显然, HBDEfRTVKP的求解效果最佳, DPSOfRTVKP和EGAfRDKP的求解效果稍差一点, 且它们求得的最差值均优于GAAfRDKP.
由表 1~表 5中的计算结果可以看出, HBDEfRTVKP的求解效果略优于DPSOfRTVKP和EGAfRDKP, 而且它们都明显优于GAAfRDKP; 3种进化算法求得各实例的最好值和平均值均非常好, 并且最好值与最优值之间相差极小; 3种进化算法的平均求解效果基本相同, 并且与RTVKP实例的规模和数据大小无关.
为了进一步说明HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP的高效性与实用性, 图 1~图 5中给出了它们求解各实例的平均收敛曲线.对每个子实例RTVKPi(0≤i≤9), 在周期Ti+1内分别取6个采样点t=Ti, Ti+Ti+1/10,
Ti+Ti+1/4, Ti+Ti+1/2, Ti+3Ti+1/4和Ti+Ti+1以及它们对应的

|
Fig. 1 Average convergence curve of Instance 1 by HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP 图 1 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例1的平均收敛曲线 |

|
Fig. 2 Average convergence curve of Instance 2 by HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP 图 2 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例2的平均收敛曲线 |
|
Fig. 3 Average convergence curve of Instance 3 by HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP 图 3 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例3的平均收敛曲线 |

|
Fig. 4 Average convergence curve of Instance 4 by HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP 图 4 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例4的平均收敛曲线 |
|
Fig. 5 Average convergence curve of Instance 5 by HBDEfRTVKP, DPSOfRTVKP and EGAfRDKP 图 5 HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP求解实例5的平均收敛曲线 |
由图 1~图 5中的平均收敛曲线不难看出, 对于RTVKP的每一个子实例, HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP都能在不超过随机变化周期1/10的时间内求得一个很好的近似值, 甚至是最优值, 这表明3种算法只需要很少的迭代次数(当然也是很少的时间)就能求得RTVKP的较好近似解或最优解, 因此它们对于具有较小随机变化周期的RTVKP问题都是非常有效和实用的.
通过对以上计算结果的比较和对平均收敛曲线的分析, 我们可以得出以下结论.
结论2. 对于实例1~实例5, HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP的各种求解结果均远远优于GAAfRDKP.从算法求得最好值的能力来看, HBDEfRTVKP比其他两种算法相对较强, 而DPSOfRTVKP和EGAfRDKP的能力基本相当, 但是从3种算法求得的平均值来看, 它们的求解效果相差不大, 这表明3种进化算法的平均求解能力基本上是相当的.
虽然理论上DPfRTVKP和DPMfRDKP[13]都能求得RTVKP问题的最优解, 但由于它们是伪多项式时间算法, 当RTVKP实例的规模较大而且物品价值和重量均匀分布在一个大范围内时(例如, Av=Aw=1, Bv=Bw=1012), 将导致所有物品价值之和与背包载重都非常大, 使DPfRTVKP和DPMfRDKP求解RTVKP各子实例所耗费的时间巨大, 从而导致求解失败.但是这种情况对于HBDEfRTVKP, DPSOfRTVKP, EGAfRDKP和GAAfRDKP是不存在的, 因为可以通过放缩法对RTVKP实例中物品的价值、重量和背包载重统一进行适当的缩小, 然后再利用它们进行求解, 因此它们对于大规模且具有大数据的难RTVKP实例都是适用的, 只是GAAfRDKP的求解效果比3种进化算法明显相差许多而已.
事实上, 对于进化算法而言, 不存在最好, 只有最适合.即不能简单地说某一进化算法最好, 另一进化算法最差, 只能是针对给定的具体问题, 比较哪种进化算法最适宜求解, 哪种进化算法不适宜求解.此外, 在求解大规模NPC问题时, 如果找不到更有效的近似算法, 那么利用进化算法求解往往是一种更明智的选择.
综上所述, 容易给出以下的结论.
结论3. 对于大规模、大数据且振荡频率较大的难RTVKP实例, 精确算法和近似算法一般不适于求解, 而算法HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP不受这些因素的影响, 它们不但求解速度快, 而且还能获得非常好的近似解, 甚至是最优解, 因此它们是求解RTVKP问题的非常高效且实用的进化算法.
5 结束语本文首先基于动态规划法提出了求解RTVKP问题的一种新精确算法DPfRTVKP, 通过与已有精确算法的时间复杂度比较指出, 对于所有物品价值之和较小的一类RTVKP实例, DPfRTVKP比DPMfRDKP的求解速度更快.然后, 将差分演化和粒子群优化与贪心优化策略相结合给出了求解RTVKP问题的两种高效进化算法HBDEfRTVKP和DPSOfRTVKP, 并通过对5个RTVKP实例的计算与比较指出:HBDEfRTVKP, DPSOfRTVKP和EGAfRDKP均是高效的, 它们的平均求解能力基本相当, 并且均比精确算法和近似算法更适于求解大规模、大数据且振荡频率较大的难RTVKP实例.
由于RTVKP问题是一种新的动态组合优化问题, 其性质分析和算法设计研究还相对较少, 关于其高效近似算法设计是其中研究的一个重点.为此, 我们将进一步探讨利用其他进化算法(如和声搜索算法[12]、布谷鸟算法[43]等)求解RTVKP的有效方法.此外, 虽然对实例的计算结果表明利用3种进化算法求解RTVKP比利用近似算法GAAfRDKP的求解结果更优, 但是缺乏严谨的理论证明, 因此, 如何在理论上证明3种进化算法优于GAAfRDKP, 也是一个值得今后探讨的问题.
| [1] | Du DZ, Ko KI. Theory of Computational Complexity. New York: Wiley-Interscience, 2000. 1-73 . |
| [2] | Gilmore PC, Gomory RE. The theory and computation of knapsack functions. Operations Research, 1966, 14(6): 1045–1074 . [doi:10.1287/opre.14.6.1045] |
| [3] | Cord J. A method for allocating funds to investment projects when returns are subject to uncertainty. Management Science, 1964, 10(2): 335–341 . [doi:10.1287/mnsc.10.2.335] |
| [4] | Goldberg DE, Smith RE. Nonstationary function optimization using genetic algorithms with dominance and diploidy. In:Proc. of the Int'l Conf. on Genetic Algorithms. Hillsdale:L. Erlbaum Associates Inc., 1987. 59-68. |
| [5] | Wang DW, Wang JW, Wang HF, Zhang RY, Guo Z. Intelligent Optimization Methods. Beijing: Higher Education Press, 2007. 282 -302 (in Chinese with English abstract). |
| [6] | Hadad BS, Eick CF. Supporting polyploidy in genetic algorithms using dominance vectors. In:Proc. of the 6th Int'l Conf. on Evolutionary Computation. 1997. 223-234.[doi:10.1007/BFb0014814] |
| [7] | Yang S. Non-Stationary problem optimization using the primal-dual genetic algorithm. In:Proc. of the 2003 Congress on Evolutionary Computation. 2003. 2246-2253.[doi:10.1109/CEC.2003.1299951] |
| [8] | Lewis J, Hart E, Ritchie G. A comparison of dominance mechanisms and simple mutation on non-stationary problems. In:Proc. of the Parallel Problem Solving from Nature. 1998. 139-148.[doi:10.1007/BFb0056857] |
| [9] | Zhou CH, Xie AS. Dynamic niche-based self-organizing learning algorithm. Ruan Jian Xue Bao/Journal of Software, 2011, 22(8): 1738–1748 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3830&journal_id=jos [doi:10.3724/SP.J.1001.2011.03830] |
| [10] | He YC, Tian HY, Zhang XL, Wang ZW, Gao SG. Solving dynamic 0-1 knapsack problems based on dynamic programming algorithm. Computer Science, 2012, 39(7): 237–241 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201207054.htm |
| [11] | He YC, Zhang XL, Gao SG, Song C. An exact algorithm for solving random time-varying knapsack problem. Journal of Chinese Computer System, 2014, 35(4): 854–857 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-XXWX201404038.htm |
| [12] | Li N, He YC, Tian HY. Application of hybrid coding harmony search algorithm in dynamic optimization. Computer Engineering, 2012, 38(12): 237–241 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201212046.htm |
| [13] | He YC, Zhang XL, Li WB, Li X, Wu WL, Gao SG. Algorithms for randomized time-varying knapsack problems. Journal of Combinatorial Optimization, 2016, 31(1): 95–117 . [doi:10.1007/s10878-014-9717-1] |
| [14] | Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. 3rd ed.. Cambridge: MIT Press, 2009. . |
| [15] | Levitin A. Introduction to the Design & Analysis of Algorithms. 3rd ed., Pearson Education, Inc., 2012. |
| [16] | Kellerer H, Pferschy U, Pisinger D. Knapsack Problems. Berlin: Springer-Verlag, 2004. . |
| [17] | Xu ZB. Computational Intelligence-Simulated Evolutionary Computation. Beijing: Higher Education Press, 2005. (in Chinese with English abstract). |
| [18] | Li MQ, Kou JS, Lin D, Li SQ. The Foundational Theory and Application of Genetic Algorithms. Beijing: Science Press, 2003. (in Chinese with English abstract). |
| [19] | Storn R, Price K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11(4): 341–359 . [doi:10.1023/A:1008202821328] |
| [20] | He YC, Wang XZ, Liu KQ, Wang YQ. Convergent analysis and improvement of differential evolution. Ruan Jian Xue Bao/Journal of Software, 2010, 21(5): 875–885 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3486&journal_id=jos [doi:10.3724/SP.J.1001.2010.03486] |
| [21] | He YC, Wang XZ, Kou YZ. A binary differential evolution algorithm with hybrid encoding. Journal of Computer Research and Development, 2007, 44(9): 1476–1484 (in Chinese with English abstract). [doi:10.1360/crad20070905] |
| [22] | Dorigo M, Stützle T. Ant Colony Optimization. Cambridge: MIT Press, 2004. 15 -120 . |
| [23] | Poli R, Kennedy J, Blackwell T. Particle swarm optimization:An overview. Swarm Intelligence, 2007, 1(1): 33–57 . [doi:10.1007/s11721-007-0002-0] |
| [24] | He YC, Wang YQ, Liu JQ. A new binary particle swarm optimization for solving discrete problems. Computer Applications and Software, 2007, 24(1): 157–159 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JYRJ200701053.htm |
| [25] | Amiri B, Fathian M, Maroosi A. Application of shuffled frog-leaping algorithm on clustering. The Int'l Journal of Advanced Manufacturing Technology, 2009, 45(1-2): 199–209 . [doi:10.1007/s00170-009-1958-2] |
| [26] | Geem ZW, Lee KS. A new meta-heuristic algorithm for continuous engineering optimization:Harmony search theory and practice. Computer Methods in Applied Mechanics and Engineering, 2005, 194(36): 3902–3933 . [doi:10.1016/j.cma.2004.09.007] |
| [27] | Gottlieb J, Marchiori E, Rossi C. Evolutionary algorithms for the satisfiability problem. Evolutionary Computation, 2002, 10(1): 35–50 . [doi:10.1162/106365602317301763] |
| [28] | Maity S, Roy A, Maiti M. A modified genetic algorithm for solving uncertain constrained solid travelling salesman problems. Computers & Industrial Engineerin, 2015, 83(2): 273–296 . [doi:10.1016/j.cie.2015.02.023] |
| [29] | Shen XJ, Wang WW, Zheng BJ, Li YX. Modified particle swarm optimization for 0-1 knapsack problem. Computer Engineering, 2006, 32(18): 23–24 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJC200618008.htm |
| [30] | Li N, He YC, Kou YZ. Solving dynamic knapsack problems based on double-structure coding PSO. Computer Engineering and Applications, 2012, 48(7): 39–42 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201207012.htm |
| [31] | Runarsson TP, Yao X. Stochastic ranking for constrained evolutionary optimization. IEEE Trans. on Evolutionary Computation, 2000, 4(3): 284–294 . [doi:10.1109/4235.873238] |
| [32] | Coello CAC. Theoretial and numerical constraint-handling techniques used with evolutionary algorithm:A survey of the state of art. Computer Methods in Applied Mechanics and Engineering, 2002, 191(11-12): 1245–1287 . [doi:10.1016/S0045-7825(01)00323-1] |
| [33] | Michalewicz Z, Schoenauer M. Evolutionary algorithms for constrained parameter optimization problems. Evolutionary Computation, 1996, 4(1): 1–32 . [doi:10.1162/evco.1996.4.1.1] |
| [34] | Xue Y, Zhuang Y, Gu JJ, Chang XM, Wang Z. Strategy selecting problem of self-adaptive discrete differential evolution algorithm. Ruan Jian Xue Bao/Journal of Software, 2014, 25(5): 984–996 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4448&journal_id=jos [doi:10.13328/j.cnki.jos.004448] |
| [35] | Zhang LB, Zhou CG, Ma M, Sun CT. A multi-objective differential evolution algorithm based on max-min distance density. Journal of Computer Research and Development, 2007, 44(1): 177–184 (in Chinese with English abstract). [doi:10.1360/crad20070125] |
| [36] | Das S, Suganthan PN. Differential evolution:A survey of the state-of-the-art. IEEE Trans. on Evolutionary Computation, 2011, 15(1): 4–31 . [doi:10.1109/TEVC.2010.2059031] |
| [37] | Wang Y, Cai ZX, Zhang QF. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. on Evolutionary Computation, 2011, 15(1): 55–66 . [doi:10.1109/TEVC.2010.2087271] |
| [38] | Mao CY, Yu XX, Xue YZ. Algorithm design and empirical analysis for particle swarm optimization-based test data generation. Journal of Computer Research and Development, 2014, 51(4): 824–837 (in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201404013.htm |
| [39] | Li XD, Yao X. Cooperatively coevolving particle swarms for large scale optimization. IEEE Trans. on Evolutionary Computation, 2012, 16(2): 210–224 . [doi:10.1109/TEVC.2011.2112662] |
| [40] | Li XD. Niching without niching parameters:Particle swarm optimization using a ring topology. IEEE Trans. on Evolutionary Computation, 2010, 14(1): 150–169 . [doi:10.1109/TEVC.2009.2026270] |
| [41] | Chen X, Gu Q, Wang ZY, Chen DX. Framework of particle swarm optimization based pairwise testing. Ruan Jian Xue Bao/Journal of Software, 2011, 22(12): 2879–2893 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3973&journal_id=jos [doi:10.3724/SP.J.1001.2011.03973] |
| [42] | Kennedy J, Eberhart RC. A discrete binary version particle swarm optimization. In:Proc. of the 1997 Conf. on System, Man, and Cybernetices. Piscataway: IEEE Service Center, 1997. 4014 -4109 . |
| [43] | Yang XS, Deb S. Engineering optimization by cuckoo search. Int'l Journal of Mathematical Modelling and Numerical Optimization, 2010, 1(4): 330–343 . [doi:10.1504/IJMMNO.2010.035430] |
| [5] | 汪定伟, 王俊伟, 王洪峰, 张瑞友, 郭哲. 智能优化方法. 北京: 高等教育出版社, 2007. |
| [9] | 周传华, 谢安世. 一种基于动态小生境的自组织学习算法. 软件学报, 2011 , 22(8) : 1738 –1748. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3830&journal_id=jos [doi:10.3724/SP.J.1001.2011.03830] |
| [10] | 贺毅朝, 田海燕, 张新禄, 王志威, 高锁刚. 基于动态规划法求解动态0-1背包问题. 计算机科学, 2012 , 39(7) : 237 –241. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJA201207054.htm |
| [11] | 贺毅朝, 张新禄, 高锁刚, 宋超. 求解随机时变背包问题的确定性算法. 小型微型计算机系统, 2014 , 35(4) : 854 –857. http://www.cnki.com.cn/Article/CJFDTOTAL-XXWX201404038.htm |
| [12] | 李宁, 贺毅朝, 田海燕. 混合编码和声搜索算法在动态优化中的应用. 计算机工程, 2012 , 38(12) : 237 –241. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJC201212046.htm |
| [17] | 徐宗本. 计算智能--模拟进化计算. 北京: 高等教育出版社, 2005. |
| [18] | 李敏强, 寇纪松, 林丹, 李书全. 遗传算法的基本理论与应用. 北京: 科学出版社, 2003. |
| [20] | 贺毅朝, 王熙照, 刘坤起, 王彦祺. 差分演化的收敛性分析与算法改进. 软件学报, 2010 , 21(5) : 875 –885. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3486&journal_id=jos [doi:10.3724/SP.J.1001.2010.03486] |
| [21] | 贺毅朝, 王熙照, 寇应展. 一种具有混合编码的二进制差分演化算法. 计算机研究与发展, 2007 , 44(9) : 1476 –1484. [doi:10.1360/crad20070905] |
| [24] | 贺毅朝, 王彦祺, 刘建芹. 一种适于求解离散问题的二进制粒子群优化算法. 计算机应用与软件, 2007 , 24(1) : 157 –159. http://www.cnki.com.cn/Article/CJFDTOTAL-JYRJ200701053.htm |
| [29] | 沈显君, 王伟武, 郑波尽, 李元香. 基于改进微粒群优化算法的0-1背包问题求解. 计算机工程, 2006 , 32(18) : 23 –24. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJC200618008.htm |
| [30] | 李宁, 贺毅朝, 寇应展. 利用双重结构编码PSO求解动态背包问题. 计算机工程与应用, 2012 , 48(7) : 39 –42. http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201207012.htm |
| [34] | 薛羽, 庄毅, 顾晶晶, 常相茂, 王洲. 自适应离散差分进化算法策略的选择. 软件学报, 2014 , 25(5) : 984 –996. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4448&journal_id=jos [doi:10.13328/j.cnki.jos.004448] |
| [35] | 张利彪, 周春光, 马铭, 孙彩堂. 基于极大极小距离密度的多目标微分进化算法. 计算机研究与发展, 2007 , 44(1) : 177 –184. [doi:10.1360/crad20070125] |
| [38] | 毛澄映, 喻新欣, 薛云志. 基于粒子群优化的测试数据生成及其实证分析. 计算机研究与发展, 2014 , 51(4) : 824 –837. http://www.cnki.com.cn/Article/CJFDTOTAL-JFYZ201404013.htm |
| [41] | 陈翔, 顾庆, 王子元, 陈道蓄. 一种基于粒子群优化的成对组合测试算法框架. 软件学报, 2011 , 22(12) : 2879 –2893. http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=3973&journal_id=jos [doi:10.3724/SP.J.1001.2011.03973] |
 2017, Vol. 28
2017, Vol. 28


