2. 河北省特种光纤与光纤传感重点实验室(燕山大学), 河北 秦皇岛 066004;
3. 河北科技师范学院 网络技术中心, 河北 秦皇岛 066004
2. The Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province (Yanshan University), Qinhuangdao 066004, China;
3. Network Technology Center, Hebei Normal University of Science & Technology, Qinhuangdao 066004, China
社交网、交通网、通信网等领域均呈现无标度特性[1-3], 是复杂网络中常见的一种现象, 不同网络中的节点和边都承载着不同形式的负载, 且负载的承受能力是有限的.加权无标度网络是指节点和边根据权值构建成的网络[4, 5], 应用在专家网等领域.
在复杂网络中, 节点和边承担的负载是不断演化的, 具有一定的动力学特征, 当节点或边的负载大于自身容量而导致失效后, 使得失效节点或边的负载通过网络的相互连接被重新分配到相关节点或边上, 从而引起其他节点或边失效, 产生级联效应, 进而可能导致整个网络的瘫痪[6, 7], 这种由微小事件引发的连锁故障称为级联失效.在现实世界中, 由级联失效引发的故障包括北美电力网崩溃事故、Internet阻塞、交通堵塞以及经济危机等.因此, 构建合理、完善的级联失效模型, 并分析参数对级联失效的影响, 对提升网络的鲁棒性具有重要的意义[8, 9].
近年来, 级联失效的研究主要基于复杂网络, 其中以无标度网络为主, 主要是从节点的初始负载、节点容量与初始负载的关系、节点失效后负载重分配规则这3个方面进行研究.复杂网络的主要特性包括节点度、集聚系数和平均最短路径长度, 其中, 节点度(包括邻居节点度)对节点负载起到决定性作用, 其属于局域范畴; 平均最短路径长度通过介数的表达方式体现出对节点负载的影响, 其属于全局范畴; 集聚系数表示网络中节点聚集程度的系数, 与节点负载没有密切关系.在加权的复杂网络中, 还需要考虑节点权重对负载的影响.因此, 节点的初始负载通常定义为关于度、介数或者邻居度的幂函数, 幂指数是用来控制初始负载强度的参数; 负载重分配主要考虑邻居的容量、负载、度数和与失效节点的距离等因素; 节点的容量必然要大于节点的初始负载, 一般定义为关于初始负载的比例函数.在这些方面, 段等人[10]基于初始负载与度的幂函数关系, 构建关于距离和节点度的择优分配规则, 分析了负载重分配的范围和均匀性.Yin[11]和Liu[12]等人同样采用关于度的初始负载模型, 利用邻居节点度或节点能量进行负载重分配, 通过对级联失效的演化分析得出了网络的临界负载以及能量对级联失效产生影响的结论.王等人[13]构建了初始负载关于节点度与邻居节点度总和乘积的幂函数, 并利用节点度和邻居节点度总和进行择优分配, 分析幂指数与容忍参数的影响关系.Liu等人[14]利用节点介数构建网络的初始负载模型, 通过容量与负载的差值进行择优分配, 分析得出容量的容忍参数对级联失效的影响.Peng[15]和Dou等人[16]构建初始负载关于介数的幂函数, 并分析幂指数的取值范围与抗击级联失效的关系.此外, 一些文献[17-19]从有向、攻击和最小化级联失效节点数等方面进行了研究.综上所述, 对于初始负载, 只考虑局域因素的节点度数(邻居度数)不能兼顾度数小的重要节点, 如桥节点, 桥节点是网络中不同分组间通信的重要桥梁, 其负载与其特殊位置有重要关系, 利用介数能够更合理地衡量它的负载; 只考虑全局因素的介数只是从最短路径的角度分析, 而实际传输中, 节点并不一定都按照最短路径进行传输, 因此, 节点度的分析是对介数分析的完善, 单独考虑某一方面都是片面的.同样地, 对于负载重分配, 只考虑邻居的负载或度数也不够完善.此外, 上述所有文献都是基于无权网络的级联失效研究, 已有可观的成果.
然而, 在现实世界中, 加权网络是普遍存在的, 典型的例子有大型的信息网络(如Internet、电话网)、交通网络(如铁路网、航空网)、生物网络(如生物神经网、蛋白质网)、社会网络(如科学家合作网、社交网)以及电网.无权网络只是反映顶点之间是否存在相互作用, 在很多情况下, 顶点之间相互作用的强度差异起着至关重要的作用, 如神经元突触之间的连接在学习和认知过程中是不变的, 只是突触之间连接强度的变化使大脑皮层产生了新的功能.再如, Internet上的带宽、航空网中两个机场间航班数量或者座位数、专家合作网中的合作次数等都是影响系统性质的重要因素.同样, 相同网络结构中的同一节点的角色和重要性也有很大差异.如电网中的开关处于大型高压配电中心或大型信息交换中心与处于普通配电站的作用有巨大的差别.因此, 无权网络完全可以作为加权网络的一种特例, 基于加权网络的级联失效研究具有更强烈的实际需求.目前, 关于加权网的研究成果远不及无权网的研究.加权网最经典的是Barrat等人[20]提出的BBV(Barrat Barthélemy Vespignani)模型, 在此模型基础上, Zhao[21]和Ding等人[22]采用关于介数的初始负载模型, 在网络的节点的失效演化过程中涉及到边权的变化, 介数从全局的结构角度体现出节点承担的负载, 但是, 不同通信路径的选择会使得计算结果与实际结果有偏差.Wang[23]和Andrea等人[24]将权重转化为节点度乘积的幂函数进行负载重分配, 从局域的角度分析网络不发生级联失效的幂指数范围, 虽然降低了算法复杂度, 但是网络的全局结构特征对网络的变化起到至关重要的作用, 忽略全局因素会使得部分特殊位置节点的负载计算不够准确.Jin等人[25]基于有向加权网建立初始负载关于节点度和权重乘积的函数关系, 并分析了有向边的情况下容量参数的临界阈值, 其初始负载考虑了局域范围内的节点度和权值, 只是同样未涉及到全局的影响因素.综上所述, 加权网络中的节点权重对网络的构建具有重要的影响, 如何将节点权重与网络的全局和局域因素相结合, 并利用数学方法推导出参数之间的变化规律, 具有重要的研究意义.
针对以上问题, 本文基于加权的无标度网络, 研究初始负载、容量和负载重分配中的参数的相互影响关系及其对级联失效的影响, 提出一个同时考虑全局和局域因素的初始负载模型, 构建关于容量的负载重分配机制, 并分析容量中的容忍参数分别与网络抵抗级联失效的鲁棒性和初始负载中的强度参数的关系.
1 加权无标度模型和问题描述 1.1 BBV模型级联失效的分析是基于节点负载和容量展开的, 在加权无标度网络中, 以点权为驱动机制的经典模型为BBV模型, 因此, 对于加权无标度网络中的级联失效研究大多基于BBV模型及其衍生模型.BBV模型的点权、度和边权分布都服从幂率分布, 保持了无标度网络的强容错性能.
在BBV模型中, 节点i的点权wi的表达式为
| $ {{w}_{i}}=\sum\limits_{j\in N}{{{t}_{ij}}} $ | (1) |
其中, tij为节点i和j之间的边权, 且tij=tji, 当i和j之间无连接时, 则tij=0, N为网络中的节点个数.
BBV模型的构建主要包含两个步骤:增长方式和权重演化.
(1) 增长:初始网络是包含m0个节点的全连通网络, 每个时间间隔加入一个新节点nnew, 新节点与网络中已经存在的m(≤m0)个节点相连, 网络中节点i被选中与nnew相连的概率与i的点权成正比, 择优连接概率为
| $ \prod\limits_{{{n}_{new}}\to i}{=\frac{{{w}_{i}}}{\sum\nolimits_{j}{{{w}_{j}}}}} $ | (2) |
(2) 权重演化:新加入的边ennewi的权重的初始值设为t0=1, ennewi的加入会导致节点i与其邻居节点j之间的边权重新分配, 调整规则如下:
| $ {{t}_{ij}}\to {{t}_{ij}}+\Delta {{t}_{ij}} $ | (3) |
其中, Δtij与tij和节点i的权重wi相关为
| $ \Delta {{t}_{ij}}={{\delta }_{i}}\frac{{{t}_{ij}}}{{{w}_{i}}} $ | (4) |
其中, δi为节点i新增一条边所带来的额外流量负担(一般情况下, 设δi=δ=1).进而可得i的点权调整为
| $ {{w}_{i}}\to {{w}_{i}}+{{t}_{0}}+{{\delta }_{i}} $ | (5) |
当权重更新之后, 进入下一个时间轮, 直到网络构建结束.BBV模型权重演化规则如图 1所示.

|
Fig. 1 The evolution rule in weights of EH-BBV 图 1 BBV权重演化规则图 |
依据平均场理论得到最终的点权分布
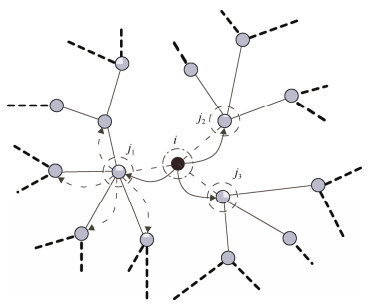
级联失效出现在现实世界中, 大多是由于单个节点受环境影响或人为因素导致失效, 出现负载分流现象, 这些分配出去的负载导致被分配的节点由于超载而失效, 出现再次负载重分配的现象, 这种现象持续发生会导致网络瘫痪.级联失效后的负载重分配示意图如图 2所示.当节点i失效后, i的负载进行重分配, 以相应的分配比例分配给节点i的邻居节点j1、j2和j3, j1节点由于超载会进行再次分配, 如此循环下去, 直到网络中不再出现节点超载的现象.
|
Fig. 2 Load redistribution after cascading failure 图 2 级联失效后的负载重分配示意图 |
此外, 级联失效的研究是基于节点负载与其容量的关系展开的, 重分配的负载与节点的初始负载有直接的关系, 因此, 节点负载的定义对后续推导参数之间的变化规律起着至关重要的作用.在网络中, 节点的负载受多方面的影响, 从全局的结构上来分析, 受到传输路径的影响, 通过节点的最短路径条数与节点的传输负载有直接的关系.另一方面, 节点局域范围内的节点度和节点权重同样与节点的传输负载密不可分.基于介数分析的负载会忽略实际中传输路径不同导致的结果偏差, 基于节点度分析的负载会忽略度数小的桥节点.因此, 如何将全局和局域因素合理、有效地结合起来, 构建综合的节点初始负载模型是本文研究的关键.此外, 各个因素中涉及到的参数和函数表达有很大差异, 如何利用数学方法进行理论推导也是研究的重点.
依据加权无标度网络的级联失效现象, 定义合理的节点负载模型和负载重分配模型, 采用不同的数学方法推导容量参数与负载参数、节点度、节点权重和介数之间的变化规律是本文研究的两个重点.对这两个研究点进行建模、研究和分析构成了本文的研究内容.探究级联失效现象的根源、过程和发展规律是本文的主要目的和目标.
2 加权网的级联失效模型 2.1 级联失效模型在以往的研究中, 初始负载与节点度、邻居度数和、介数中的一种或两种成比例关系或幂率关系, 如
| $ Loa{{d}_{m}}(0)=(1+\alpha ){{\left( {{B}_{m}}{{k}_{m}}{{w}_{m}}\sum\limits_{{m}'\in {{M}_{m}}}{{{w}_{{{m}'}}}} \right)}^{\tau }} $ | (6) |
其中, α和τ为控制节点初始负载强度的参数, 且α≥0, τ>0, Bm为节点m的介数, km为m的度数, wm为m的权重, Mm为m的邻居.公式(6) 中的Bm表示为
| $ {{B}_{m}}=\sum\limits_{i\ne j\ne m, {{k}_{m}}>1}{\frac{{{g}_{imj}}}{{{g}_{ij}}}} $ | (7) |
其中, gij表示节点对i和j之间的最短路径条数, gimj表示i和j之间通过m的最短路径条数, 这里, 对介数的条件进行了改进, 限定节点的度数大于1, 以此来避免当m度数为1时出现的负载为0的情况, 当节点的度数为1时, 设定gimj的值为0.5, 目的是在保证每个节点都有初始负载的前提下, 不影响节点介数的排序.从式(7) 中可以看出, 当τ≠1时, 节点的初始负载与节点介数呈非线性关系.
节点的初始负载是在网络不断的演化过程中形成的, 因此, 在确定节点的容量时, 可采用按需分配的原则, 使得节点的容量与节点初始负载成正比的关系, 因此可得:
| $ {{C}_{m}}=(1+\beta )Loa{{d}_{m}}(0) $ | (8) |
其中, β≥0, 为容忍系数, 用来衡量节点处理额外负载的能力.β的值越大, 说明网络处理额外负载的能力越强, 越能够抵抗级联失效, 但同时, 网络的实际成本也越大, 在网络的初始容量固定的情况下, β的值越小, 网络不发生级联失效的概率越大.
当网络中的m节点失效后, m的负载不会凭空消失, 而是分配给网络中存在的完好节点, 考虑到节点只能通过邻居节点进行传输, 该节点失效后, 其邻居节点受到的影响最大.因此, 假设m的负载会按照某种规则分配给m的邻居节点, 更新了邻居节点的负载.负载分配比例与邻居节点的容量有关, 容量大的节点将获得较大的分配比例, 由此, m的邻居节点j分配到的负载比例为
| $ Loa{{d}_{j}}({{C}_{j}})=\frac{{{C}_{j}}}{\sum\limits_{k\in {{M}_{m}}}{{{C}_{k}}}} $ | (9) |
由上式可得邻居节点j分配到的负载ΔLoadj为
| $ \Delta Loa{{d}_{j}}=Loa{{d}_{j}}({{C}_{j}})\cdot Loa{{d}_{m}} $ | (10) |
以上完成了一次失效节点的负载重分配过程, 当更新后的节点j的负载超出其容量时, 导致j失效, 触发新一轮的负载重分配过程, 该过程可能会引发更多的节点失效, 使得网络出现级联失效现象, 直到网络中不再出现负载过载的现象为止.假设网络中的总节点数为N, 每一轮有一个节点i失效, 级联失效过程后存活的节点总数为CNi, 则利用CF来衡量网络的鲁棒性, CF的表达式[26]如下所示:
| $ CF=\frac{\sum\limits_{i=1}^{N}{C{{N}_{i}}}}{N(N-1)} $ | (11) |
从式中可以看出, CF的值越大, 表示网络的鲁棒性越强, 越能够抵抗网络的级联失效现象, 能够简明、直观地反映网络的性能, 便于后续对级联失效的演化分析.
2.2 算法的时间复杂度分析网络中有N个节点, 在最坏情况下进行时间复杂度分析.首先分析介数的时间复杂度, 需要每个节点寻找与其他节点间的最短路径, 采用Dijkstra算法的时间复杂度为O(N2), 节点度和节点权重的时间复杂度为O(1), 邻居节点权重和的时间复杂度为O(N).节点负载由介数、节点度、节点权重和邻居节点权重和构成, 计算的时间复杂度为O(N2+N), 节点容量与节点负载成比例关系, 时间复杂度也为O(N2+N), 当负载进行重分配时, 需要计算节点邻居节点的容量和, 最坏情况下的时间复杂度为O(N).因此, 节点进行负载重分配所需要的时间复杂度为O(N2+N+N), 最终为O(N2).
3 级联失效模型解析基于上述给出的节点初始负载和容量的表达式以及节点失效后的负载重分配规则, 对级联失效进行深层次的理论分析, 解析出各个参数之间的变化关系.
当节点m失效后, m的负载会分配到其邻居节点j, 节点j出现了一次负载更新, 要保证j不出现失效现象则需要满足以下条件:
| $ Loa{{d}_{j}}+\Delta Loa{{d}_{j}}\le {{C}_{j}} $ | (12) |
将公式(6)、公式(8)~公式(10) 代入式(12) 中, 可得:
| $ Loa{{d}_{j}}+\frac{{{\left( {{B}_{j}}{{k}_{j}}{{w}_{j}}\sum\limits_{{j}'\in {{M}_{j}}}{{{w}_{{{j}'}}}} \right)}^{\tau }}}{\sum\limits_{k\in {{M}_{m}}}{{{\left( {{B}_{k}}{{k}_{k}}{{w}_{k}}\sum\limits_{{k}'\in {{M}_{j}}}{{{w}_{{{k}'}}}} \right)}^{\tau }}}}Loa{{d}_{m}}\le (1+\beta )(1+\alpha ){{\left( {{B}_{j}}{{k}_{j}}{{w}_{j}}\sum\limits_{{j}'\in {{M}_{j}}}{{{w}_{{{j}'}}}} \right)}^{\tau }} $ | (13) |
由于在实际环境中, 节点的负载是只增不减的, 因此, 所有节点的负载都不会低于它们的初始负载, 即
| $ Loa{{d}_{m}}\ge Loa{{d}_{m}}(0)=(1+\alpha ){{\left( {{B}_{m}}{{k}_{m}}{{w}_{m}}\sum\limits_{{m}'\in {{M}_{m}}}{{{w}_{{{m}'}}}} \right)}^{\tau }} $ | (14) |
| $ Loa{{d}_{j}}\ge Loa{{d}_{j}}(0)=(1+\alpha ){{\left( {{B}_{j}}{{k}_{j}}{{w}_{j}}\sum\limits_{{j}'\in {{M}_{j}}}{{{w}_{{{j}'}}}} \right)}^{\tau }} $ | (15) |
将式(14) 和式(15) 代入到式(13) 中, 并化简可得:
| $ \frac{{{\left( {{B}_{m}}{{k}_{m}}{{w}_{m}}\sum\limits_{{m}'\in {{M}_{m}}}{{{w}_{{{m}'}}}} \right)}^{\tau }}}{\sum\limits_{k\in {{M}_{m}}}{{{\left( {{B}_{k}}{{k}_{k}}{{w}_{k}}\sum\limits_{{k}'\in {{M}_{j}}}{{{w}_{{{k}'}}}} \right)}^{\tau }}}}\le \beta $ | (16) |
在无标度网络中, 研究已得节点度与介数分别服从幂率分布
| $ \frac{{{\left( k_{m}^{(\gamma -1)/(\delta -1)+1}{{w}_{m}}\sum\limits_{{m}'\in {{M}_{m}}}{{{w}_{{{m}'}}}} \right)}^{\tau }}}{\sum\limits_{k\in {{M}_{m}}}{{{\left( k_{k}^{(\gamma -1)/(\delta -1)+1}{{w}_{k}}\sum\limits_{{k}'\in {{M}_{j}}}{{{w}_{{{k}'}}}} \right)}^{\tau }}}}\le \beta $ | (17) |
通过复杂网络理论[29], 依据贝叶斯公式可得:
| $ \sum\limits_{n\in {{M}_{i}}}{{{w}_{n}}}=\sum\limits_{v=1}^{N}{{{w}_{i}}p({{{{w}'}}_{v}}|{{w}_{i}}){{{{w}'}}_{v}}} $ | (18) |
其中, p(w'v|wi)表示某权值为wi的节点的邻居节点权值为w'v的条件概率, 由于无标度网络及其衍生出的网络是度度无关的, 因此可得:
| $ p({{{w}'}_{v}}|{{w}_{i}})=\frac{{{{{w}'}}_{v}}p({{{{w}'}}_{v}})}{\langle w\rangle } $ | (19) |
将式(19) 带入到式(18) 中可得:
| $ \sum\limits_{n\in {{M}_{i}}}{{{w}_{n}}}={{w}_{i}}\sum\limits_{v=1}^{N}{\frac{{{{{w}'}}_{v}}^{2}p({{{{w}'}}_{v}})}{\langle w\rangle }}=\frac{{{w}_{i}}\langle {{w}^{2}}\rangle }{\langle w\rangle } $ | (20) |
因此, 式(17) 可以表达为
| $ \frac{k_{m}^{\tau (\gamma -1)/(\delta -1)+\tau }w_{m}^{\tau +1}{{\left( \frac{\langle {{w}^{2}}\rangle }{\langle w\rangle } \right)}^{\tau }}}{\sum\limits_{k\in {{M}_{m}}}{\left( k_{k}^{\tau (\gamma -1)/(\delta -1)+\tau }w_{k}^{\tau +1}{{\left( \frac{\langle {{w}^{2}}\rangle }{\langle w\rangle } \right)}^{\tau }} \right)}}=\frac{k_{m}^{\tau (\gamma -1)/(\delta -1)+\tau }w_{m}^{\tau +1}}{\sum\limits_{k\in {{M}_{m}}}{\left( k_{k}^{\tau (\gamma -1)/(\delta -1)+\tau }w_{k}^{\tau +1} \right)}}\le \beta $ | (21) |
将上式化简为以下形式:
| $ \frac{k_{m}^{\tau (\gamma -1)/(\delta -1)+\tau }w_{m}^{\tau +1}}{\sum\limits_{k\in {{M}_{m}}}{{{\left( k_{k}^{\frac{\tau (\gamma -1)/(\delta -1)+\tau }{\tau +1}} \right)}^{\tau +1}}w_{k}^{\tau +1}}}\le \beta $ | (22) |
设
| $ \sum\limits_{k \in {M_m}} {(k_k^A{w_j})} = k_m^A\sum\limits_{v = 1}^N {p\left( {\mathit{k'}_\mathit{v}^\mathit{A}{{\mathit{w'}}_\mathit{v}}\mathit{|k}_\mathit{m}^\mathit{A}{\mathit{w}_\mathit{m}}} \right)} \mathit{k'}_\mathit{v}^\mathit{A}{\mathit{w'}_\mathit{v}} $ | (23) |
由于无标度网络是度度无关的网络, 因此,
| $ p\left( {\mathit{k'}_\mathit{v}^\mathit{A}{{\mathit{w'}}_\mathit{v}}\mathit{|k}_\mathit{m}^\mathit{A}{\mathit{w}_\mathit{m}}} \right)= \frac{{\mathit{k'}_\mathit{v}^\mathit{A}{{\mathit{w'}}_\mathit{v}}\mathit{p}(\mathit{k'}_\mathit{v}^\mathit{A}{{\mathit{w'}}_\mathit{v}})}}{{\left\langle {{k^A}w} \right\rangle }} $ | (24) |
由上可得:
| $ \sum\limits_{\mathit{k}\in {{\mathit{M}}_{\mathit{m}}}}{(\mathit{k}_{\mathit{k}}^{\mathit{A}}{{\mathit{w}}_{\mathit{k}}})}=\mathit{k}_{\mathit{m}}^{\mathit{A}}\sum\limits_{\mathit{v}=1}^{\mathit{N}}{{\mathit{{k}'}_{\mathit{v}}^{\mathit{A}}{{{\mathit{{w}'}}}_{\mathit{v}}}\mathit{p}(\mathit{{k}'}_{\mathit{v}}^{\mathit{A}}{{{\mathit{{w}'}}}_{v}})\mathit{{k}'}_{\mathit{v}}^{\mathit{A}}{{{\mathit{{w}'}}}_{v}}}/{\langle {{\mathit{k}}^{\mathit{A}}}\mathit{w}\rangle }\;}={\mathit{k}_{\mathit{m}}^{\mathit{A}}\langle {{(\mathit{k}_{\mathit{v}}^{\mathit{A}})}^{2}}\rangle \langle {{\mathit{w}}^{2}}\rangle }/{(\langle {{\mathit{k}}^{A}}\rangle \langle \mathit{w}\rangle )}\; $ | (25) |
进一步可得:
| $ \sum\limits_{k\in {{M}_{m}}}{{{(k_{k}^{A}{{w}_{k}})}^{\tau +1}}}\, ={k_{m}^{A}\langle {{({{k}^{A}}w)}^{\tau +2}}\rangle }/{\langle {{k}^{A}}w\rangle }\;={k_{m}^{A}\langle {{({{k}^{A}})}^{\tau +2}}\rangle \langle {{w}^{\tau +2}}\rangle }/{(\langle {{k}^{A}}\rangle \langle w\rangle )}\; $ | (26) |
将式(26) 代入到式(22) 中, 化简可得:
| $ \frac{k_{m}^{A\tau }w_{m}^{\tau +1}\langle {{k}^{A}}\rangle \langle w\rangle }{\langle {{k}^{A(\tau +2)}}\rangle \langle {{w}^{\tau +2}}\rangle }\le \beta $ | (27) |
由于β的值涉及到实际的成本问题, 因此, β的值越小越好.此外, 在加权网的形成过程中, 节点度k和w的初始值都为1, 并在网络的演化过程中只会增加不会减少, 因此, 式(27) 中的km和wm的最小值kmin和wmin为1.由此, 可以简化公式, 并得到了β的最小值.
在加权无标度网络中, 已经证实节点度和权重的分布幂率是相同的.因此, 分布函数可表示为p(s)=cs-α, 通常情况下, 2<α<3, 则根据概率统计理论得出
| $ \langle s\rangle =\frac{c}{-\alpha +2}\left[{{s}^{-\alpha +2}} \right]_{{{s}_{\min }}}^{{{s}_{\max }}}=\frac{c}{-\alpha +2}s_{\min }^{-\alpha +2}\left( {{N}^{-\frac{\alpha -2}{\alpha -1}}}-1 \right) $ | (28) |
| $ \langle {{s}^{n}}\rangle =\frac{c}{n-\alpha +1}\left[{{s}^{n-\alpha +1}} \right]_{{{s}_{\min }}}^{{{s}_{\max }}}=\frac{c}{n-\alpha +1}s_{\min }^{n-\alpha +1}\left( {{N}^{\frac{n-\alpha +1}{\alpha -1}}}-1 \right) $ | (29) |
其中, 0<n<α-1, 并把kmin和wmin代入到式(27) 中可得:
| $ \beta \ge \frac{k_{\min }^{A\tau }w_{\min }^{\tau +1}\langle {{k}^{A}}\rangle \langle w\rangle }{\langle {{k}^{A(\tau +2)}}\rangle \langle {{w}^{\tau +2}}\rangle }\, =k_{\min }^{-A}\frac{(A(\tau +2)-\gamma +1)(\tau -{{\gamma }^{w}}+3)}{(A-\gamma +1)(-{{\gamma }^{w}}+2)}\times \frac{{{N}^{\frac{A-\gamma +1}{\gamma -1}}}-1}{{{N}^{\frac{A(\tau +2)-\gamma +1}{\gamma -1}}}-1}\times \frac{{{N}^{\frac{-{{\gamma }^{w}}+2}{{{\gamma }^{w}}-1}}}-1}{{{N}^{\frac{\tau -{{\gamma }^{w}}+3}{{{\gamma }^{w}}-1}}}-1} $ | (30) |
其中, γ和γw分别为节点度和权重分布的幂率指数, 且2<γ<3, 2<γw<3, 当N很大时, 上式可化简为
| $ \beta \ge k_{\min }^{-A}\frac{(A(\tau +2)-\gamma +1)(\tau -{{\gamma }^{w}}+3)}{(A-\gamma +1)(-{{\gamma }^{w}}+2)} $ | (31) |
由τ、γ和γw的取值范围可得-γw+2<0且τ-γw+3>0, 因此, 为了满足β≥0, 可推出不等式:
| $ \left\{ \begin{align} &A(\tau +2)-\gamma +1\ge 0 \\ &A-\gamma +1<0 \\ \end{align} \right. $ | (32) |
将A的值代入上式得到:
| $ \left\{ \begin{align} &\tau \ge \frac{(\gamma \delta -3\gamma -3\delta +5)+\sqrt{{{(3\gamma +3\delta -\gamma \delta -5)}^{2}}+4(\gamma +\delta -2)(\gamma -1)(\delta -1)}}{2(\gamma +\delta -2)} \\ &\tau <\frac{(\gamma -1)(\delta -1)}{(\gamma -2)(2-\delta )+1} \\ \end{align} \right. $ | (33) |
当γ取值在(2, 3) 之间时, 由相关研究已知δ的值为2.2[19], 当γ取值为2时, τ的取值范围近似为(0.76, 1.21);当γ取值为3时, τ的取值范围近似为[0.44, 3], 合并得到τ的取值范围在[0.44, 3]内.
将A代入式(31) 中, 得到β的最终表达式为
| $ \beta \ge k_{\min }^{-\frac{\tau (\gamma +\delta -2)}{(\delta -1)(\tau +1)}}\frac{(\tau (\gamma +\delta -2)(\tau +2)-(\gamma -1)(\delta -1)(\tau +1))(\tau -{{\gamma }^{w}}+3)}{(\tau (\gamma +\delta -2)-(\gamma -1)(\delta -1)(\tau +1))(-{{\gamma }^{w}}+2)} $ | (34) |
式(34) 给出容量参数β关于最小度数kmin、度分布幂率指数γ、权值分布幂率指数γw和初始负载参数τ的关系, 通过设置部分变量的值, 可以分析其余变量与β的变化关系, 进而分析β与对抗级联失效和增强网络鲁棒性的关系.
4 实验分析为了更好地反映本文提出的基于加权无标度网络的级联失效模型中参数之间的变化关系, 本节将使用MATLAB工具, 在BBV模型的基础上, 构建一个容量有限的加权无标度拓扑, 并在该拓扑中对网络中初始负载参数、度分布幂率指数、权重分布幂率指数与容量参数的变化规律进行仿真.此外, 还将容量参数对网络鲁棒性的影响进行仿真分析.
4.1 级联失效参数分析首先给出加权无标度网的拓扑实例以及对数坐标下节点度和权重的分布图, 如图 3和图 4所示.该拓扑基于BBV加权模型, 考虑到现实环境中节点容量是有限的, 将节点的传输范围进行限制, 依据无标度网络的增长和择优连接机制构建一个局域范围内的加权无标度拓扑[30].在监测区域内随机布撒了200个节点, 新加入的节点连接到网络中两个不同的节点.从图 3可以看出, 小部分节点的度数总和几乎覆盖了整个网络, 满足无标度网络的定义.从图 4可以看出, 对数坐标下的网络中节点度和权重分布都具有明显的拖尾现象, 符合幂率分布的特征.

|
Fig. 3 The weighted scale-free topology 图 3 加权无标度拓扑图 |

|
Fig. 4 The degree and weight distribution 图 4 度分布和权重分布图 |
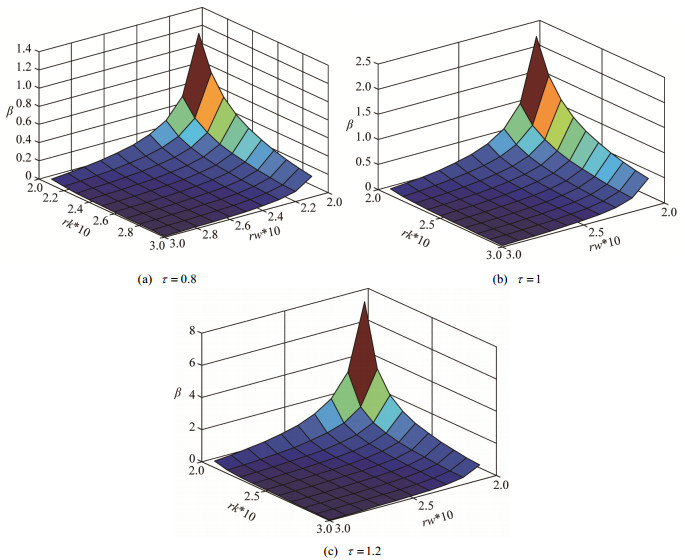
图 5给出容量参数β与度分布指数和权重分布指数的变化规律.
|
Fig. 5 The surface of threshold β with the degree distribution scale γ and weight distribution scale γw under the condition of different τ 图 5 不同τ值下的β与γ和γw的关系曲面图 |
在图 5中, 介数指数δ=2.2, 最小度kmin=1, 度分布指数γ和权重分布指数γw在2~3范围内, 图 5(a)~图 5(c)分别对应初始负载参数中τ为0.8、1、1.2情况下, γ和γw与β的变化关系.从图中可以看出, γ和γw的值越小, β的值越大, 表明幂率指数越小, 则网络的鲁棒性越差, 因此, 需要增大节点的容量, 即增大β值, 以抵抗级联失效现象, 这是由于, 幂率指数越低, 网络越不均匀, 当攻击网络中度数大的节点时会使网络迅速瘫痪.此外, 从图中还可以看出, 随着τ的增大, β也会增大, 这是由于容量与初始负载是成比例的关系, 而τ用来控制初始负载的强度, 所以, τ增大时, 即初始负载增大, β自然会增大.
图 6给出最小度kmin与容量参数β的变化关系.

|
Fig. 6 The surface of threshold β with the degree distribution scale γ and weight distribution scale γw under the condition of different kmin 图 6 不同kmin值下的β与γ和γw的关系曲面图 |
在图 6中, δ=2.2, 当τ=1时, γ和γw的值在2~3内, 图 6(a)~图 6(c)分别对应kmin为2、5、10情况下, γ和γw与β的变化关系.从图中可以看出, kmin的值越大, β的值越小, kmin与β是负相关的, 这是由于无标度网络中的最小度值通常与新节点加入网络时所连的边数m相关, m越大, 则kmin越大, 而网络的平均度为2m.因此, kmin越大, 表示网络的平均度越大, 网络越稳定, 则需要的β值越小, 这与已有的相关研究成果相吻合.
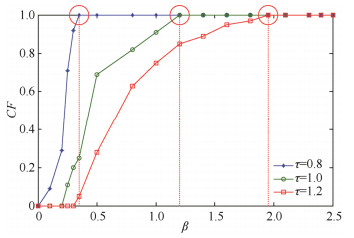
4.2 鲁棒性分析为了分析参数β对网络鲁棒性CF的影响, 将采用最大负载攻击方式, 移除网络中的节点, 进而分析该攻击方式下β与CF的变化规律, 如图 7所示.
|
Fig. 7 The CF-β curves 图 7 β值与网络鲁棒性CF的关系图 |
其中, kmin=2, γ和γw的取值为3.从图 7可以看出, τ的值越大, 网络的鲁棒性越差, 需要增大β的值来提高网络的鲁棒性.在τ的取值分别为0.8、1和1.2时, 网络鲁棒性达到1时对应的β值分别为0.35、1.2和1.95, 与理论得出的值0.35、1.19和1.93非常接近, 证明了理论的准确性和有效性.
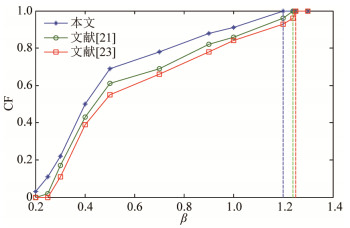
为证实所提方法能够使无标度网络达到更强的抵制级联失效的鲁棒性, 在kmin=2, τ=1, γ和γw的取值为3的条件下, 将本文的方法分别与只以节点度定义的初始负载模型(文献[23])和只以介数定义的初始负载模型(文献[21])所提方法的鲁棒性进行对比, 结果如图 8所示.
|
Fig. 8 The CF-β curves under different strategies 图 8 不同策略下网络鲁棒性CF与β值的关系图 |
从图 8可以看出, 在相同的网络条件下, 当网络达到最强鲁棒性时, 本文中β=1.2, 文献[21]中β=1.4, 文献[23]中β=1.5, 本文所提方法在网络达到最强鲁棒性时需要的β值最小, 说明此策略下的网络更难发生级联失效, 同时也证明了节点初始负载定义的准确度更高.文献[21]略优于文献[23]的原因是无标度网络的介数分布具有很强的异质性.在这种网络中, 介数大的中心节点会有许多最短路径经过, 极易过载, 所以, 给这些中心节点分配更大的权重能够显著提高网络鲁棒性.不过, 综合考虑节点度和介数, 才会使网络的鲁棒性最强.
4.3 抵抗级联失效能力对比分析为了分析所提方法抵抗级联失效的能力, 将本文提出的方法分别与文献[23]和文献[21]中的方法进行对比.抵抗级联失效能力与容量分配方式直接相关, 而容量分配与负载直接相关.通过上述3种方法的研究内容可知, 节点容量与初始负载的比例值十分接近, 由此可得, 节点初始负载定义的准确性和合理性直接关系到网络抵抗级联失效的能力.因此, 将通过对比初始负载定义的准确性来分析该性能.在节点初始容量相同的条件下, 采用最大负载攻击方式移除网络中的节点, 统计网络CF值, 以此来衡量初始负载定义的准确性.网络节点的最小度数kmin=2, 并取α=0, τ=1, 网络度分布和权重分布的幂率指数γ和γw为3.对比结果如图 9所示.

|
Fig. 9 Comparison of the resistance for cascading failure 图 9 抵抗级联失效能力对比图 |
负载定义越准确, 移除最大负载的攻击方式使得网络出现的级联失效节点越多, 鲁棒性CF值越低.从图 8可以看出, CF值最低的是本文所提方法, 其次是关于节点度的文献[23]和关于介数的文献[21], 节点度的效果略优于介数的部分原因是实验背景采用的是加权无标度网络, 无标度的特性使得网络中的节点度分布极其不均匀, 度数之间的巨大差异体现了节点度因素的重要性.但是, 全局结构角度的介数因素同样是不可忽略的.结合全局和局域因素是本文所提方法效果最优的主要原因.
5 结束语本文在加权无标度网络的基础上, 从全局和局域的角度提出了一种参数可调的级联失效模型, 建立了节点介数、度数和权重与初始负载的关系, 进而给出容量与初始负载的关系, 依据网络不出现级联失效的条件推导出负载参数与容量参数的关系, 并通过给出的鲁棒性表达式作为衡量指标, 对模型进行仿真分析, 实验结果表明, 该模型准确地分析了级联失效的各参数之间的变化关系以及参数的取值范围, 并在此基础上, 增强了网络的鲁棒性, 延长了网络的寿命.下一步研究的重点为降低节点负载重分配的时间复杂度, 并依据实际需求分析被分配节点的动态负载, 使负载重分配更加合理.
| [1] |
Barabasi AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509–512.
[doi:10.1126/science.286.5439.509] |
| [2] |
Ma YT, He KQ, Li B, Liu J. Empirical study on the characteristics of complex networks in networked software. Ruan Jian Xue Bao/Journal of Software, 2011, 22(3): 381–407(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/3934.htm [doi:10.3724/SP.J.1001.2011.03934] |
| [3] |
Yang B, Liu DY, Liu J, Jin D, Ma HB. Complex network clustering algorithms. Ruan Jian Xue Bao/Journal of Software, 2009, 20(1): 54–66(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/3464.htm [doi:10.3724/SP.J.1001.2009.00054] |
| [4] |
Milchtaich I. Network topology and equilibrium existence in weighted network congestion games. Int'l Journal of Game Theory, 2015, 44(3): 515–541.
[doi:10.1007/s00182-014-0443-9] |
| [5] |
Boccaletti S, Latora V, Moreno Y, Chavez M, Hwanga DU. Complex networks: Structure and dynamics. Physics Reports, 2006, 424(4): 175–308.
[doi:10.1016/j.physrep.2005.10.009] |
| [6] |
Thai MT, Pardalos PM.Handbook of Optimization In Complex Networks.Springer-Verlag, 2012.[doi: 10.1007/978-1-4614-0754-6] |
| [7] |
Buldyrev SV, Parshani R, Paul G, Stanley HE, Havlin S. Catastrophic cascade of failures in interdependent networks. Nature, , 464(7291): 1025–1028.
[doi:10.1038/nature08932] |
| [8] |
Leonardo DO, Srivishnu MV. Cascading failures in complex infra-structure systems. Structural Safety, 2009, 31(6): 157–167.
[doi:10.1016/j.strusafe.2008.06.007] |
| [9] |
Cupac V, Liziera JT, Prokopenko M. Comparing dynamics of cascading failures between network-centric and power flow models. Electrical Power and Energy Systems, 2013, 49: 369–379.
[doi:10.1016/j.ijepes.2013.01.017] |
| [10] |
Duan DL, Zhan RJ. Evolution mechanism of node importance based on the information about cascading failures in complex networks. Acta Physica Sinica, 2014, 63(6): 068902(in Chinese with English abstract).
[doi:10.7498/aps.63.068902] |
| [11] |
Yin RR, Liu B, Liu HR, Li YQ. The critical load of scale-free fault-tolerant topology in wireless sensor networks for cascading failures. Physica A, 2014, 409: 8–16.
[doi:10.1016/j.physa.2014.02.001] |
| [12] |
Liu HR, Dong MR, Yin RR, Han L. Cascading failure in the wireless sensor scale-free networks. Chinese Physics B, 2015, 24(5): 050506.
[doi:10.1088/1674-1056/24/5/050506] |
| [13] |
Wang JW, Rong LL, Wang D. Model for cascading failures on complex networks based on local characteristics of nodes. Journal of Management Sciences in China, 2010, 13(8): 42–50(in Chinese with English abstract).
http://www.cnki.com.cn/Article/CJFDTOTAL-JCYJ201008004.htm |
| [14] |
Liu YN, Li X, Chen SZ, Qin Z. Model for cascading network failures based on the nodes with different tolerance parameter. The Journal of China Universities of Posts and Telecommunications, 2011, 18(5): 95–101.
[doi:10.1016/S1005-8885(10)60109-4] |
| [15] |
Peng XZ, Yao H, Du J, Wang Z, Ding C. Invulnerability of scale-free network against critical node failures based on a renewed cascading failure model. Physica A, 2015, 421: 69–77.
[doi:10.1016/j.physa.2014.11.024] |
| [16] |
Dou BL, Wang XG, Zhang SY. Robustness of networks against cascading failures. Physica A, 2010, 389: 2310–2317.
[doi:10.1016/j.physa.2010.02.002] |
| [17] |
Wang JW, Jiang C, Qian JF. Robustness of Internet under targeted attack: A cascading failure perspective. Journal of Network and Computer Applications, 2014, 40: 97–104.
[doi:10.1016/j.jnca.2013.08.007] |
| [18] |
Nie L, Liu JJ, Zhang HC, Xu ZW. On the inapproximability of minimizing cascading failures under the deterministic threshold model. Information Processing Letters, 2014, 114(1): 1–4.
[doi:10.1016/j.ipl.2013.10.007] |
| [19] |
Fang XL, Yang Q, Yan WJ. Modeling and analysis of cascading failure in directed complex networks. Safety Science, 2014, 65: 1–9.
[doi:10.1016/j.ssci.2013.12.015] |
| [20] |
Barrat A, Barthélemy M, Vespignani A. Modeling the evolution of weighted networks. Physical Review E, 2004, 70(6): 066149.
[doi:10.1103/PhysRevE.70.066149] |
| [21] |
Zhao Z, Zhang P, Yang HJ. Cascading failures in interconnected networks with dynamical redistribution of loads. Physica A, 2015, 433: 204–210.
[doi:10.1016/j.physa.2015.03.030] |
| [22] |
Ding L, Zhang SY. Cascading failures-oriented weighting strategies on complex networks. Control and Decision, 2013, 28(9): 1399–1408(in Chinese with English abstract).
[doi:10.13195/j.kzyjc.2013.09.006] |
| [23] |
Wang WX, Chen G. Universal robustness characteristic of weighted networks against cascading failure. Physical Review E, 2008, 77: 026101.
[doi:10.1103/PhysRevE.77.026101] |
| [24] |
Asztalos A, Sreenivasan S, Szymanski BK, Korniss G. Distributed flow optimization and cascading effects in weighted complex networks. European Physical Journal B, 2012, 85: 288.
[doi:10.1140/epjb/e2012-30122-3] |
| [25] |
Jin WX, Song P, Liu GZ, Stanley HE. The cascading vulnerability of the directed and weighted network. Physica A, 2015, 427: 302–325.
[doi:10.1016/j.physa.2015.02.035] |
| [26] |
Wang JW, Rong LL. Robustness of the western United States power grid under edge attack strategies due to cascading failures. Safety Science, 2011, 49(6): 807–812.
[doi:10.1016/j.ssci.2010.10.003] |
| [27] |
Goh KI, Kahng B, Kim D. Universal behavior of load distribution in scale-free networks. Physical Review Letters, 2001, 87(27): 278701.
[doi:10.1103/PhysRevLett.87.278701] |
| [28] |
Alexei V, Romualdo PS, Alessandro V. Large-Scale topological and dynamical properties of Internet. Physical Review E, 2002, 65: 066130.
[doi:10.1103/PhysRevE.65.066130] |
| [29] |
Marián B, Romualdo PS. Epidemic spreading in correlated complex networks. Physical Review E, 2002, 66(4): 047104.
[doi:10.1103/PhysRevE.66.047104] |
| [30] |
Han L, Liu B, Li YQ, Zhao LJ. Studies on weighted scale-free topology in energy heterogeneous wireless sensor network. Acta Physica Sinica, 2014, 63(15): 150504(in Chinese with English abstract).
[doi:10.7498/aps.63.150504] |
| [2] |
马于涛, 何克清, 李兵, 刘婧. 网络化软件的复杂网络特性实证. 软件学报, 2011, 22(3): 381–407.
http://www.jos.org.cn/1000-9825/3934.htm [doi:10.3724/SP.J.1001.2011.03934]
|
| [3] |
杨博, 刘大有, LiuJiming, 金弟, 马海宾. 复杂网络聚类方法. 软件学报, 2009, 20(1): 54–66.
http://www.jos.org.cn/1000-9825/3464.htm [doi:10.3724/SP.J.1001.2009.00054]
|
| [10] |
段东立, 战仁军. 基于相继故障信息的网络节点重要度演化机理分析. 物理学报, 2014, 63(6): 068902.
[doi:10.7498/aps.63.068902]
|
| [13] |
王建伟, 荣莉莉, 王铎. 基于节点局域特征的复杂网络上相继故障模型. 管理科学学报, 2010, 13(8): 42–50.
http://www.cnki.com.cn/Article/CJFDTOTAL-JCYJ201008004.htm
|
| [22] |
丁琳, 张嗣瀛. 面向级联失效的复杂网络加权策略. 控制与决策, 2013, 28(9): 1399–1408.
[doi:10.13195/j.kzyjc.2013.09.006]
|
| [30] |
韩丽, 刘彬, 李雅倩, 赵磊静. 能量异构的无线传感器网络加权无标度拓扑研究. 物理学报, 2014, 63(15): 150504.
[doi:10.7498/aps.63.150504]
|
 2017, Vol. 28
2017, Vol. 28


