2. 南京大学 计算机科学与技术系, 江苏 南京 210023
2. Department of Computer Science and Technology, Nanjing University, Nanjing 210023, China
自组织增量学习神经网络(self-organizing incremental neural network,简称SOINN)是一种基于竞争学习的神经网络模型[1, 2, 3],能够对数据进行增量式的无监督学习.SOINN使用一组分布在特征空间上的神经元来近似输入数据的密度分布,这些神经元之间的连接构成一个或者多个连通子图,每个子图都代表SOINN发现的一个聚类以及该聚类的拓扑结构.
不同于传统的竞争型神经网络,SOINN没有固定的拓扑结构,它根据输入的数据以及若干简单的规则自适应地调整局部神经元的权值以及神经元之间的连接.SOINN的学习算法是完全增量式的,这不仅表现在学习过程的在线性(on-line)上,更为重要的是学习结果的增量性.由于采用了自适应调整的相似度阈值(similarity threshold)来识别之前没有学习过的输入模式,该网络能动态地生成新的神经元来表示输入模式,同时不影响其之前的学习结果.
由于以上这些特点,SOINN作为一种通用的竞争神经网络模型,已经在各个领域中得到了应用,包括机器人智能、计算机视觉、医学诊断、异常检测等等.除此之外,SOINN已经被改进和调整来处理更为多样化的机器学习问题,包括联想记忆、模式分类、密度估计、流形学习等等.
本文尽可能全面地梳理并总结SOINN的基本思想、后续改进以及在不同研究领域中的应用情况.第1节介绍SOINN的研究背景和一些基本问题.第2节具体介绍原始SOINN以及后续的一些改进,并讨论关于SOINN的一些具体问题.第3节介绍SOINN是如何进行调整以用于监督学习、联想记忆等不同学习问题的.第4节总结SOINN在各个领域的一些具有代表性的应用并作简要介绍.第5节讨论SOINN进一步的发展方向.第6节对全文进行总结.
1 研究背景聚类和拓扑学习是无监督学习的两个重要部分,两者都试图从无标签的数据集中发现隐含的信息.聚类算法的目的是为了挖掘出数据中潜在的全局结构信息,而拓扑学习则关注数据的局部邻域信息,这种局部信息能够在一定程度上反映原始数据在特征空间上的拓扑结构.历史上有多种竞争型神经网络模型被提出用于解决这两类问题,比较有代表性的是Kohonen提出的自组织映射网(self-organizing map,简称SOM)[4, 5]和Martinetz等人提出的Neural Gas(简称NG)[6]和Topology Representing Network(简称TRN)[7].这些网络都具有类似的学习机制,预设一定数量的神经元随机分布在某个空间(可以是原始数据空间,如NG和TRN;也可以是一个低维空间,用于把原始数据映射过来以达到降维的目的,如SOM),并初始化它们的连接以确定初始的网络拓扑结构,然后逐个输入数据样本进行训练.训练过程中,所有神经元相互竞争对当前输入的响应权力,获胜的神经元更新自身参数以适应新的输入.这样的竞争机制导致最终网络收敛后的结果是不同区域的神经元对不同的输入模式更为敏感,一旦该模式出现,就会有更大的几率在竞争中被激活.因此,竞争神经网络是一种实现模式识别的模型.然而有研究表明,这样的竞争神经网络难以在保持可塑性的情况下获得稳定的学习结果.这就是Grossberg和Carpenter提出的稳定性-可塑性困境(stability-plasticity dilemma)[8]:在试图构造一个能够实时地适应不断变化的环境的自适应学习系统时,如果一个系统过于稳定,则不善于适应快速变化的环境;反之,系统对外界的刺激过于敏感,就会导致系统本身没有办法稳定地保存先前学习到的知识,甚至无法收敛到一个稳定的状态.因此,在面对缺乏先验知识且外部输入模式随时间变化的情况时,网络的自组织性和算法的增量性是一个学习系统应该具有的特性.
随着移动互联网、社交媒体等新兴模式的快速发展,流式大数据正普遍成为数据挖掘与分析的对象,其主要特点是实时性、易失性、突发性、无序性、无限性[9].在对流式数据的分析过程中出现的概念漂移(concept drift)现象同样会造成稳定性-可塑性困境:算法面对非稳态的输入时(non-stationary environment),如何学习新的模式而不影响过去学习的结果,是急需解决的问题.以聚类为例,传统的聚类算法大致可分为层次化的聚类算法、划分式聚类算法、基于密度和网格的聚类算法这几类[10],其中具有代表性的有经典的基于划分的k-means[11]算法及其多种改进版本[12, 13, 14, 15],此类算法的突出问题是几乎只适用于各向同性性质(isotropic)的聚类簇,对初始聚类中心点很敏感,而且需要预先指定聚类数目.相比之下,基于混合模型假设并使用EM[16]算法来求解概率模型能够对更加一般的数据进行聚类,但同样需要预先指定混合成分的概率分布形式或者聚类的数量.基于图的划分的谱聚类算法[17]同样也面临着确定聚类数目的问题.而且,以上算法均无法处理输入中隐含的聚类结构随时间发生变化的情况.因此,在缺乏先验知识且面对需要快速处理的流式数据时,常用的算法往往没有考虑输入数据的动态性.
提出稳定性-可塑性困境的同时,Grossberg和Carpenter提出了后来影响力极大的竞争神经网络模型:自适应共振理论(adaptive resonance theory,简称ART)[8, 18, 19]试图解决这个问题.此后,越来越多的研究者们提出了多种不同竞争网络模型来适应这一问题,其中的大多数基于SOM和NG的结构和算法,最具有代表性的模型之一是Fritzke提出的Growing Cell Structures[20]和Growing Neural Gas[21]网络(简称GNG).其中,神经元可以随着输入数据动态地增加.因此,GNG比NG网络具有 更强的动态性,能够适应变化的输入模式,但是稳定性较差. SOINN在SOM和GNG的基础上更进一步增强了网络的可塑性,同时又增加了删除噪声节点、自适应调整阈值参数等操作来稳定学习的结果.
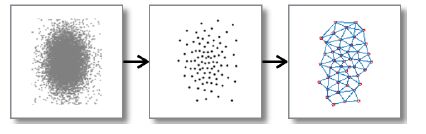
2 SOINN算法思想及其改进 2.1 原始SOINNSOINN[1]是两层结构(不包括输入层)的竞争性神经网络,它以自组织的方式对输入数据进行在线聚类和拓扑表示.其工作过程如图 1所示.
|
Fig. 1 Two stages of competitive learning in SOINN 图 1 SOINN的两层竞争学习示意图 |
· 第1层网络接受原始数据的输入,以在线的方式自适应地生成原型(prototype)神经元来表示输入数据.需要注意的是:在SOINN,SOM,GNG这类网络中的神经元与常见的前馈神经网络中的神经元是不一样的概念,它们可以被看作是某个特征空间中的向量,而它们的权值(weight)就是神经元在该空间中的坐标表示,之后也会用节点来指代这里的神经元.这些节点和它们之间的连接反映了原始数据的分布情况以及拓扑结构;
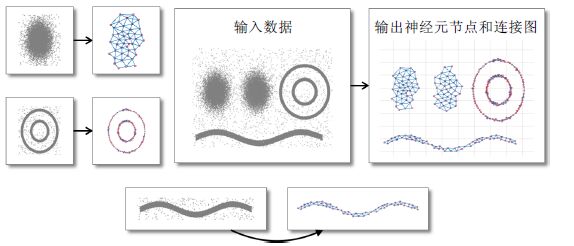
· 第2层根据第1层网络的结果估计出原始数据的类间距离与类内距离,并以此作为参数,把第1层生成的神经元作为输入再运行一次SOINN算法,以稳定学习结果.如图 2所示:当输入数据存在多个聚类并存在噪声时,SOINN依然能够生成可靠的神经元节点来表示输入数据中的各个聚类;同时,子图的拓扑结构反映了原始数据分布的性质.
|
Fig. 2 Experiment on artificial dataset 图 2 人造数据集上的效果演示 |
从具体算法的角度来看,SOINN的训练过程主要分为4步:神经元的分布、动态节点调整、拓扑表示以及去噪过程.下面分别介绍每个部分的基本思路.
2.1.1 分布神经元用一定数量的代表性数据来近似原始的完整数据集,然后在这些代表点的基础上对新来的数据做出决策,是基于原型(prototype-based)的学习算法的基本思想.这些代表性的数据被称为原型(prototype),它们通常以某种方式反映了原始数据的分布信息,比如k-means的各个聚类中心,就是一种典型的原型.SOINN也是一种基于原型的算法,它的原型由分布在输入空间中的神经元组成,每个神经元代表了它周围与它最相似的输入模式.从这个方面看,分布神经元本质上是一种矢量量化过程.
矢量量化(vector quantization,简称VQ)[22]最初用于对数字信号进行压缩编码,使得能够以较低的带宽来传输信号.简单来说,VQ的过程就是用一组固定数量的码书(codebook)向量wi(i=1,2,…,k)对原始信号x进行编码,以达到数据压缩的目的.在固定了wi之后,对x的编码过程就是寻找与之最接近的向量wi(x)来表示x.因而,这个问题最后归结为找到一组向量wi,使得在解码端信号重建的期望误差值E(w)最小化:
| $E(w)=\int{||x-{{w}_{i(x)}}||_{2}^{2}p(x)\text{d}x}$ | (1) |
其中,p(x)是信号x的概率密度函数.E(w)通常情况下并没有闭合形式的最优解,需要通过迭代算法来进行优化,其中最为广泛使用的是基于Lloyd-Max条件[23, 24]的LBG算法[25]来近似求解.LBG算法是一种批处理算法,不能直接用于增量学习.对公式(1)使用随机梯度下降进行优化得到以下更新式,但通常需要遍历多次训练数据才能使算法收敛到局部最优解:
| $w_{i}^{(t+1)}\leftarrow w_{i}^{(t)}+\alpha (t)({{x}^{(t)}}-w_{i}^{(t)})$ | (2) |
其中,$w_{i}^{(t)}$为第t步时与输入向量x(t)最接近的码书向量的权值,a(t)为更新步长.
在公式(2)的基础上增加一个邻域函数来控制不同码书向量对输入的敏感程度,可以形成具有空间有序性的映射[4],这在许多竞争神经网络中已经得到了验证.此时,对码书向量的更新式见公式(3):
| $w_{i}^{(t+1)}\leftarrow w_{i}^{(t)}+\alpha (t)h({{x}^{(t)}},W,\sigma )({{x}^{(t)}}-w_{i}^{(t)})$ | (3) |
其中,W={w1,w2,…,wk},s是调整邻域函数的参数.通常情况下,h的存在使得只有距离输入模式最近的那些码书向量能够参与竞争并向输入数据移动,这些向量或者在输入空间相邻(如NG,TRN,GNG等),或者在神经元所在的低维空间相邻(SOM等).网络收敛的结果是输出的码书向量与输入模式间形成一种空间有序的映射关系,即,相邻的向量编码相似的输入模式.Kohonen[4]对这种现象做了深入讨论,指出这种空间有序的映射关系在人脑的神经元中也普遍存在.
对于SOINN来说,它的神经元就相当于矢量量化中的码书向量.SOINN并没有显式地定义邻域函数h,在每次新到来输入数据时,只有最邻近的神经元(通常称为胜者节点)以及与它在拓扑结构上的邻居节点(两者有边相连接)有移动的机会,这是由于SOINN生成的神经元之间的连接能够保持输入数据的拓扑邻域系.SOINN为每个神经元都赋予了一个不同的学习率(learning rate)参数e(t),作用与VQ中a(t)相同,其中,t为该神经元成为胜者的次数且e(t)与t成反比.其意义在于:使得神经元的移动最终能趋于稳定,算法最终能够收敛而不至于持续震荡.通常情况下,e(t)的形式需要满足一定的条件,以保证最终的学习效果.SOINN使用的是Robbins等人[26]提出的约束条件:
| $\sum\limits_{t=1}^{\infty }{\varepsilon (t)}=\infty ,\sum\limits_{t=1}^{\infty }{{{\varepsilon }^{2}}(t)}<\infty $ | (4) |
满足公式(4)的学习率,保证了每个节点在逐渐稳定的情况下始终保持一定的学习能力.
文献[27]中对矢量量化的渐近性质做了分析,指出:在算法收敛后,量化向量w的密度r(x)与原数据集密度函数p(x)具有如下关系:
| $\rho \left( x \right)\mu p{{\left( x \right)}^{a}}$ | (5) |
其中,a被称为放大因子(magnification factor).使用不同的算法来优化函数(1),会得到不同的a值.
Villmann 等人[28]总结了常用向量量化算法的放大因子,并给出了几种调整的方法.
2.1.2 动态调整动态调整是SOINN实现自组织和增量学习的关键,它使得神经元的权值向量和网络的拓扑结构能够随着输入模式的到来动态地进行调整,以优化对输入数据的表达精度.此外,通过适时增加神经元不仅能够自适应地确定神经元的数量以满足一定的量化误差约束,同时还能在不影响之前学习结果的情况下适应之前没有学习过的输入模式.SOINN分别定义了类内节点插入(within class insertion)和类间节点插入(between class insertion)操作来达到这两个目的.
类内的节点插入操作主要是为了自适应地减小神经元的量化误差,尽可能准确地近似原始数据的分布.具体的,SOINN在运行过程中会记录每个神经元的累积量化误差,每学习一段固定的时间之后,找出所有节点中累积量化误差最大的两个节点,然后在它们的中间插入一个新的节点,以插值的方式更新它们的累计量化误差值.考虑到并非每次插入操作都是有必要的,如果不进行一些限制的话,那么随着算法的进行,节点的数量会不断地增加.因此,SOINN在每次类内的节点插入操作后都会再判断该次插入操作是否显著降低了量化误差:如果没有,则取消本次插入操作.
类间节点插入发生在新输入的数据与之前学习过的数据差异性较大的时候.SOINN通过为每一个神经元i设置一个相似度阈值(similarity threshold)参数Ti来判断新来的数据样本是否有可能属于一个新的类别:如果该数据点与之前学习得到神经元差异性较大,就在该数据点的位置上生成一个新的节点来代表这个可能的新模式.如图 3所示,x为新输入的数据点,SOINN首先找到与其最相似的两个神经元s1与s2,如果$d({{s}_{1}},\xi )>{{T}_{{{s}_{1}}}}$或者$d({{s}_{1}},\xi )>{{T}_{{{s}_{2}}}}$,就认为数据点x的差异性较大.其中,d(×)为相似度度量函数(通常为欧氏距离函数).新生成的节点并不意味着最终一定属于一个新的聚类,只是在当前的相似度阈值下,该输入与之前学习到的模式存在较大差异.随着越来越多的输入模式得到学习,相似度阈值和神经元之间的连接也在不断变化.
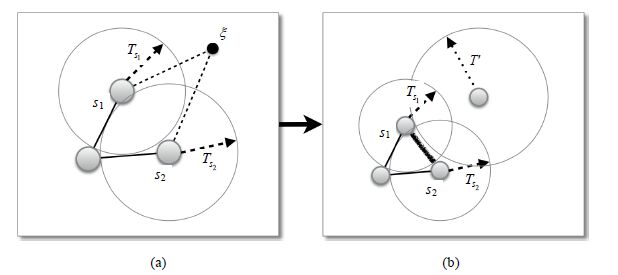
|
Fig. 3 Between class insertion 图 3 类间节点插入 |
如果新输入的数据样本不满足节点插入的条件,SOINN首先找到获胜的两个节点s1和s2,然后以公式(2)的形式对它们的权值W1,W2Rn进行更新.这样,在神经元数量固定的情况下,SOINN的调整过程实际上等价于传统的矢量量化过程.
可以看出:类间节点插入是SOINN实现增量学习的关键,节点插入的时机对于最终的结果有较大影响,而每个节点的相似度阈值参数T又是决定插入操作的关键.如果T值过小,则每个数据都会被认为是一个新的模式而生成一个节点;T值过大,则会导致节点个数过少,此时量化误差增大,而且不能准确反映数据的分布.理想情况下,该参数应大于平均的类内距离同时小于平均的类间距离[29].ART使用一个名为Vigilance的参数来判断输入模式是否是一种没有学习过的新模式,然而对于不同的输入数据,由于它们的分布不同,类内距离和类间距离也会相应不同,因此,参数Vigilance是问题相关的.GNG同样也面临着手动选择阈值的问题.SOINN在这个问题上采用了一种自适应的方式不断更新Ti的值,使得能够适应不断变化的输入模式.假设N为所有节点的集合,Ni为节点i的邻居节点集合.如果Ni不为空,即,存在其他节点通过一条边与其相连,就令:
| ${{T}_{i}}=\underset{j\in {{N}_{i}}}{\mathop{\max }}\,||{{W}_{i}}-{{W}_{j}}||$ |
否则,${{T}_{i}}=\underset{j\in N\backslash \{i\}}{\mathop{\min }}\,||{{W}_{i}}-{{W}_{j}}||$.
可以看出,这两个定义实际上是当前对最大类内距离和最小类间距离的估计值.图 3和图 4分别演示了在节点插入和权值更新的过程中,相似度阈值是如何变化的.实际应用表明,这样的动态调整方法是行之有效的.
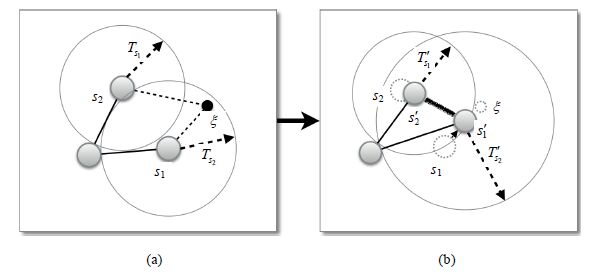
|
Fig. 4 Updating the weights of neurons 图 4 更新神经元权值 |
2.1.3 拓扑表示
神经元的动态调整,是为了对数据进行增量式的学习.此外,SOINN还采用了竞争Hebb学习规则(competitive hebbian learning,简称CHL)来建立神经元之间的连接.Martinetz和Schulten[7]已经证明了:用这种方法建立的连接,能够形成神经元集合的Delaunay三角剖分(delaunay triangulation)的子图;同时,这种子图在神经元足够稠密的条件下,能够完美保持原始数据的拓扑邻域关系.
CHL可以简要概括如下:每输入一个数据样本,在特征空间中找出与该输入模式最相似的两个神经元,然后把它们连接起来.图 3(b)和图 4(b)中加粗的连接就是根据CHL建立起来的新连接.但考虑到SOINN在运行过程中会调整节点的位置,因此随着算法的进行,之前距离比较近的两个节点可能在算法结束时不再被一个输入信号给同时激活了,因此,它们之间不应该存在连接.为此,每条连接都通过一个参数age来记录它们经历了多少次数据的输入.每次该边连接的两个端点被同时激活时,就重置该参数为0;否则,该参数超过了一定的阈值就会使得相应的连接被删除.
2.1.4 网络去噪在实际应用中,输入数据中往往存在噪声或者离群点,这会导致SOINN为它们生成不必要的节点(因为它们往往与之前学习到的模式差异性较大).另一方面,随机地输入顺序也会使得SOINN的结果出现不稳定的现象,这是基于竞争学习的神经网络所面临的一个主要问题.为了缓解这一问题,在算法运行过程中,SOINN周期性(周期由自定义参数l决定)地查找并删除可能处于密度较低区域的部分节点,因为这种节点很可能是由于数据中存在噪声点产生的,不能反映原始数据的分布信息.此外,在两个距离比较近的聚类交界处,数据点的密度也会明显低于聚类的中心区域,因此删除这部分的节点以及与它相关的连接,使SOINN能够稳定地把两个不同的聚类区别开来.
在SOINN中,一个节点成为胜者的次数和它的邻居个数被用来判断它是否处于数据密度较低的区域.如果一个节点没有或者只有一个邻居节点,而且成为胜者的次数低于当前神经元的平均次数一定比例就会被删除,同时移除所有与它相关联的边,其中,自定义参数c用于控制这个比例.节点的删除操作使得SOINN在有噪声的环境下具有一定的鲁棒性,而参数l决定了SOINN进行去噪过程的频率,通过调整它,以适应不同的输入环境.
2.1.5 完整算法描述SOINN自提出以来经历了若干调整与改进,但是总体框架并没有发生变化.下面是其简要算法描述.
算法1. SOINN.
1) 初始化神经元集合A={c1,c2},其中:神经元c1,c2的权重W1,W2Rn是随机的两个初始数据样本;初始化边集合CAxA为空集,即,神经元之间没有初始连接;
2) 输入一个新的数据样本(或是信号、模式):xRn;
3) 找出A中与x中最相似的两个神经元,s1和s2,其中,
| ${{s}_{1}}=\underset{c\in A}{\mathop{\arg \min }}\,||\xi -{{W}_{c}}||$ | (6) |
| ${{s}_{2}}=\underset{c\in A\backslash \{{{s}_{1}}\}}{\mathop{\arg \min }}\,||\xi -{{W}_{c}}||$ | (7) |
如果$||\xi -{{W}_{{{s}_{1}}}}||>{{T}_{{{s}_{1}}}}$或者$||\xi -{{W}_{{{s}_{2}}}}||>{{T}_{{{s}_{2}}}}$成立,就为x生成一个新的节点r,令A=A{r},Wr=x;
4) 如果s1与s2间不存在连接,令C=C{(s1,s2)},即,为两个最相似节点建立连接;
令$ag{{e}_{({{s}_{1}},{{s}_{2}})}}=0$,即,刷新边(s1,s2)的年龄参数;
5) 与胜者节点相连的所有边age参数加1:
| $ag{{e}_{({{s}_{1}},i)}}=ag{{e}_{({{s}_{1}},i)}}+1,\forall i\in {{N}_{i}}$ | (8) |
6) 累加胜者节点的局部量化误差:
| ${{E}_{{{s}_{1}}}}={{E}_{{{s}_{1}}}}+||\xi -{{W}_{{{s}_{1}}}}||$ | (9) |
7) 如果没有建立新的节点,则更新两个胜者节点的权值:
| ${{W}_{{{s}_{1}}}}={{W}_{{{s}_{1}}}}+\varepsilon (t)(\xi -{{W}_{{{s}_{1}}}})$ | (10) |
| ${{W}_{{{s}_{2}}}}={{W}_{{{s}_{2}}}}+{\varepsilon }'(t)(\xi -{{W}_{{{s}_{2}}}})$ | (11) |
其中,$\varepsilon (t)=\frac{1}{t},{\varepsilon }'(t)=\frac{1}{100t}$.
8) 检查所有连接(i,j)C当前的年龄参数age(i,j):如果age(i,j)>agemax,就从C移除该连接.其中,agemax是预先定义的参数;
9) 如果当前输入的数据样本总数是l的整数倍(即,经过了一个学习周期),检查整个SOINN进行类内节点插入操作和去噪过程.
如果还有输入,就跳转至第(2)步;否则停止算法,输出神经元集合A和连接矩阵C.
2.2 Enhanced SOINNSOINN提出之后,Shen和Hasegawa[2]提出了Enhanced-SOINN(简称E-SOINN)来解决原始SOINN的一些不足.
1) 原始SOINN的两层模型意味着需要判断在训练过程中何时停止第1层的学习转而学习第2层,但是在在线学习的过程中,通常很难选择合适的时机;
2) 用于减小量化误差的类内节点插入在第1层网络中效果并不明显,因为第1层的相似度阈值是根据数据的分布自适应调整的.后续的应用表明,在这一层神经元的数量通常是足够多的,所以并不会有比较大的量化误差;
3) 在两个数据的聚类重叠区域密度较大时,SOINN往往不能够把这两个类别区分开来,因此聚类效果有待提高.
对此,E-SOINN在结构上只保留了原始SOINN的第1层,并移除了类内节点插入操作以简化训练过程,使得E-SOINN更加适合实时的增量式学习.在算法上,增加了一个新的分离与合并子类的过程,该过程与节点删除操作一样是周期性进行的.它的作用是检测出类别间的重叠区域,并删除处于该区域的神经元和与之相关联的边,达到分离这些存在重叠区域的聚类的目的.实验显示,E-SOINN能够以更少的参数、更简单的模型获得比两层SOINN更加稳定的结果.
需要指出的是:根据Zhang等人的分析[30],类内节点插入操作的作用并不仅限于减小量化误差,它还能使得SOINN生成足够密集的神经元,这缓解了增量学习中由数据的输入次序所带来的不稳定问题.因而,是否需要类内节点插入操作有时需要根据具体应用需求来决定.
2.2.1 节点密度E-SOINN对两个具有重叠区域的聚类进行分离的过程是基于以下假设的:重叠区域处于类别的边缘,且在此区域中数据分布的密度明显低于聚类内部或者中心点处的密度.图 5是一种典型的情况,两个聚类发生了重叠,A和B分别是两个聚类的中心,C为重叠区域的一部分,A点和B点的密度明显大于位于重叠区域的C点.
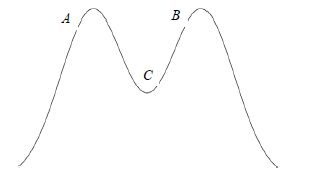
|
Fig. 5 Overlapped density 图 5 重叠的密度区域 |
数据分布的密度信息可以从已经生成的神经元中得到估计,一个很自然的想法是:神经元成为胜者的次数应当与其所在区域的数据点密度成正比,这样,被激活的次数就能够作为密度的一种度量方式.但事实上,从SOINN的竞争性来看,最终算法稳定时,每个神经元被激活的概率是趋于相同的.因此,该参数并不能作为密度的度量.E-SOINN使用了每个神经元到它的邻居节点的平均距离来度量其所在区域的数据点密度,这是由于神经元的移动总是趋向于周围数据密集的区域,因而该区域中神经元的相互距离也会相应较小.应当注意的是:这并不是数据密度分布的一个估计,只是作为一种密度大小的度量来找出空间中高密度的区域.
2.2.2 分离和合并子类根据之前第2.2.1节的假设和节点间距离所带来的密度信息,E-SOINN使用算法2对学习得到的神经元网络进行划分子类的操作.
算法2. 划分子类.
1) 找出具有密度的局部最大值的神经元,分别赋予它们不同的类别标记,其中,局部最大值是相对于所有邻居节点来定义的;
2) 其余节点的类别设置为与它们相连接的局部最大值点的类别;
3) 如果某一个节点具有多个不同的类别标记,则认为该节点处于重叠区域内.
这样,就在E-SOINN的神经元网络中根据密度划分出了多个子类,Shen等人在文献[2]中指出:在实际运行中,E-SOINN使用的方法反映的密度信息往往并不是如图 5所示一样是平滑的,因此会导致一些不必要的分离操作.为此,E-SOINN还使用了一些其他的方法来合并子类.这两个操作使得E-SOINN能够区分出重叠密度较大的两个聚类,获得比SOINN更加可靠的聚类效果.
2.3 其他改进在E-SOINN之后,对SOINN的改进主要有两个方向:一是把SOINN应用于监督学习中,简化SOINN算法用于快速生成不同类别的代表神经元;另一个方向是改进SOINN在非监督学习中的性能,重点是提高其分离重叠聚类簇和面对不同输入次序时的稳定性.
Adjusted SOINN是E-SOINN的一种简化形式,它对SOINN的调整属于上述的第1种情况,主要用于监督的学习过程中.因为已经有了类别信息,因此它删除了E-SOINN的分离去除子类的过程.Adjusted SOINN大部分的应用场景是为不同的类别生成代表节点,这样可以在丢弃输入数据的情况下,以较少的代价保存不同类别的关键信息,用于之后的处理过程.一个具体的应用是Adjusted SOINN Classifier(ASC)[31].
Load Balancing SOINN(简称LB-SOINN)[30]对SOINN的调整属于第2种,其在E-SOINN的基础上提出了3点主要的改进:
1) 提出了负载均衡(load balancing)的概念,其中,负载指的是神经元的学习次数(learning time),即,成为胜者的次数,然后采用类内的节点插入方法来平衡神经元的负载;
2) 使用了一套基于Voronoi区域划分的算法来合并已经分离的子类,合并的过程是从密度高的神经元开始,避免了E-SOINN可能出现的反复分离又合并子类的震荡情况;
3) 把多种相似度衡量方式进行组合作为SOINN对节点距离的度量方式,并根据数据的维度赋予不同的权重,使得SOINN在高维空间也有很好的表现.
文中指出:如果神经元的数量足够多,而且在学习过程中每个神经元的负载保持大致接近,最后生成的神经元的拓扑结构对数据的输入顺序以及神经元的初始位置不敏感,从而可以获得更为稳定的结果.从实验结果来看:LB-SOINN能够获得比E-SOINN更加稳定的聚类效果,同时也能够很好地处理文本分类这种特征维度较高的学习问题.
Local Distribution SOINN(简称LD-SOINN)[32, 33]也是对SOINN稳定性的一种改进.对于原始SOINN以及其他后续的改进来说,我们注意到:每个胜者神经元从生成到被删除,它的权值W要么不变,要么以公式(10)、公式(11)的形式进行更新.假设某神经元到某一时刻共经历N次更新,则第n轮的权值由如下公式进行更新:
| ${{W}^{n}}={{W}^{n-1}}+\frac{1}{n}({{\xi }^{n}}-{{W}^{n-1}}).$ |
稍作运算,我们能够得到:
| ${{W}^{N}}=\frac{1}{N}\sum\limits_{n=1}^{N}{{{\xi }^{n}}}.$ |
因此,每个SOINN中的神经元最终的权值就是所有用于更新该神经元的训练样本的均值.从统计的角度上来说,每个神经元保留了局部样本的一阶矩信息.基于此观察,LD-SOINN试图通过为每个神经元维护局部协方差矩阵来保留更为丰富的样本信息,来提高SOINN的稳定性.
每个LD-SOINN中的神经元都维护一个局部协方差矩阵S,该矩阵保存了落在该神经元接受阈范围内所有样本的二阶矩信息.假设这些样本的个数为N,我们知道该协方差矩阵的最大似然估计为
| ${{\Sigma }^{N}}=\frac{1}{N}\sum\limits_{t=1}^{N}{({{\xi }^{n}}}-{{W}^{N}}){{({{\xi }^{n}}-{{W}^{N}})}^{T}}.$ |
其中,x,W的定义都与前文相同.为了使得算法能够保持增量性,该矩阵同样以等价的迭代形式进行更新.
| ${{\Sigma }^{n}}={{\Sigma }^{n-1}}+\frac{1}{{{n}^{2}}}[(n-1)({{\xi }^{n}}-{{W}^{n-1}}){{({{\xi }^{n}}-{{W}^{n-1}})}^{T}}-n{{\Sigma }^{n-1}}].$ |
通过同时保留局部样本的均值和协方差信息,每个神经元实际上维护了一个局部的高斯分布,因此算法中也不再使用欧式距离来度量某个样本到神经元的距离,取而代之的是使用协方差矩阵加权过的马氏距离.此外,每训练一定时间,距离相近而且分布相似的神经元将被合并,以减少神经元的数量.这使得整个网络的复杂度始终得到有效的控制,增加了模型的稳定性.如图 6所示,面对与图 2相同的输入数据,LD-SOINN对数据的描述比只利用一阶信息的SOINN更加简洁,图中每个椭圆都描述了一个神经元和由它的协方差矩阵所确定的高斯分布.从图中可以看出:当数据近似以高斯分布的形式存在时,LD-SOINN几乎可以完美地回复出该聚类的所有信息(左边的两个高斯分布);当该条 件不满足时,由于LD-SOINN的自适应性以及多个高斯分布的近似能力,LD- SOINN依然能够近似地还原出输入数据的分布(两个环形分布和一个正弦形状分布).
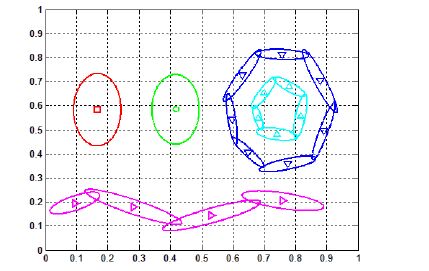
|
Fig. 6 Learning output of LD-SOINN [33] 图 6 LD-SOINN的学习结果 |
LD-SOINN不仅从算法上对SOINN进行了改进,使得每个神经元的表达能力更为丰富,它同时也给SOINN提供了概率上的解释.尽管细节上有诸多不同,从模型的本质来看,LD-SOINN所做的改进实际上使得SOINN成为了一种增量式的高斯混合模型,每个神经元成为了一个动态的高斯成分拟合它周围的训练样本,可以被动态生成也可以被动态删除,具有相当高的灵活性.而训练该模型的方法就是对每个神经元的参数分别做最大似然估计,由于每输入一个样本模型参数都能够得到更新,因此相比于EM算法训练的高斯混合模型,LD-SOINN训练的速度更快,收敛需要的样本数也大大减少.原始SOINN可以被看成是协方差矩阵为单位矩阵的特殊情况,这为理解SOINN这一类算法提供了不一样的视角.
2.4 参数讨论
原始SOINN总共有8个参数,分别是λ,agemax,c,α1,α2,α3,
· λ是SOINN进行去噪以及类内节点插入的周期.当输入中包含较多噪声时,应当设置相应较小的λ值,使得算法能够及时删除因为噪声而产生的节点和连接.在一些人工数据或者几乎没有噪声的情况下,尽量增大λ的值可以使得SOINN为数据集生成足够多的节点以减少量化误差,同时具有更好的拓扑保持性质;
· agemax决定了一对神经元间的连接在不被刷新的情况下,最多能存在多少个单位时间(输入的次数).这个参数的存在,是由SOINN增量学习的特点所决定的.因为神经元在整个训练过程中可能会增加或移动,刚开始相邻的两个节点在一段时间之后也许并不相邻,此时,两个神经元间存在的连接应该被消除,否则就违反了CHL规则.因此,agemax对最终生成的网络拓扑结构有较大影响,其值通常不宜太大.因为由于输入次序的随机性,难免出现误生成的连接,它们都应当在一段合适的时间窗内被删去.通常情况下,数据流形的结构越复杂,agemax的值应该越小来保证拓扑结构的正确性.根据实际应用不同,50~100的取值在大多数情况下都比较适用;
· c值是进行节点删除时使用的一个阈值参数,通常设置为0.5~1.0之间.山崎和博等人针对SOINN的各个参数进行了详细的实验,论证了参数之间是如何相互作用以及对最终的输出有怎样的影响[34].
3 基于SOINN的学习算法基于原型的无监督学习算法扩展为有监督的分类算法是非常自然的,可以首先对每个类别的样本集分别应用无监督算法进行学习来分别得到它们的原型,然后基于这些原型做最邻近分类,比如基于SOM的一系列Learning Vector Quantization(LVQ)算法[35].目前,已经有许多基于SOINN的监督学习算法已经被提出,它们无一例外都把SOINN的增量学习性质引入了传统的分类算法中,使得分类器的训练可以更加灵活高效.除此之外,SOINN的算法思想也被用在了密度估计和流形学习中,下面简要介绍其中具有代表性的工作.
3.1 监督学习SOINN最初被设计用于进行无监督学习,对原始数据进行表示、聚类以及拓扑学习.当学习任务从无监督学习变为分类时,对算法有了不同的要求.在聚类时,为了能够得到尽可能准确的聚类结果,SOINN需要相对较多的节点来代表原始数据,这些节点以及它们的连接提供了关于数据的分布信息以及拓扑结构.然而对于分类问题来说,类的边界信息才是最终分类的关键信息.
基于这个观察,Adjusted SOINN Classifier(简称ASC)[31]在训练过程中保留那些对分类决策有帮助的节点以加速后续的分类过程.其训练过程分为以下4个阶段.
1) 首先,对每个类别的数据分别使用Adjusted SOINN进行学习,得到各个类的代表神经元集合;
2) 考虑到SOINN的结果会受到输入数据的顺序影响,为了使算法更加稳定,再对代表每个类别的神经元使用k-means算法进行调整,使得它们收敛到稳定的位置;
3) 如果一个节点的类别与它的k近邻节点进行多数表决得到的类别不同时,删除该节点.该思想来自ENC(k-edited neighbors classifier)[36],目的是提高最终最邻近分类的性能;
4) 检测并删除对分类没有帮助的中心节点.
如图 7所示,最左边的图是原始的输入数据,中间的是Adjusted SOINN为每个类别生成的神经元,最右图为ASC算法运行后的结果.可以看出:在所有Adjusted SOINN生成的节点中,只有与分类相关的边界节点被保留了下来,它们对最终的分类有决定性的影响.由于删去了大部分对分类无关的节点,算法在实际分类时只需要较小的时间与空间开销.
ASC是完全基于SOINN框架的分类器,由于额外的节点清理操作,它并不是一个完全在线的算法.但是当SOINN与其他基于原型的分类器相结合时,往往能够使得该算法具有较好的增量学习性质.Zheng[37]和Xu[38]等人分别将SOINN与LVQ,SVM相结合,使得这两种算法获得了增量学习的能力.
3.2 半监督学习和主动学习SOINN也被改进,用于实现增量式的半监督学习和主动学习[39, 40].利用了SOINN,能够实现数据压缩的性质,相应的算法对学习中标注样本(半监督学习)的数量或是询问次数(主动学习)的要求都较低.
对于半监督学习,首先使用E-SOINN中的方法,每隔一段固定的学习时间找到当前具有密度极大值的节点,并用它们把SOINN分离为许多子类,然后找到可能处于决策边界上的节点和边.由于SOINN产生的节点密度并不是一个连续的分布,这种方法会产生很多不正确的分割,因此采用了密度差的方法判断是否要把两个相邻的子类进行合并.如果一个子类中存在一个带类标的节点,则把整个子类标注为该教师节点的类别;否则,在同一个合并类中存在教师节点,就把子类标注为该教师节点的类别.在上述过程中,如果找到多个教师节点,就使用密度最大的那个节点的类别.
主动学习的算法通常期望查询的次数越少越好,因此每次只询问对标注影响力最大的节点.这些节点包括每个子类中密度最大的节点、合并类中密度最大的节点以及子类相邻边界上的节点.SOINN通过询问这些最有可能影响分类效果的节点来进行主动学习,因此只需要进行少量的询问也能获得令人满意的学习效果.
3.3 联想记忆和基于模式的推理神经网络用于联想记忆有很长的历史,历史上提出了许多著名的联想记忆系统和算法,如知名的Hopfield网络[41],但它们往往对可联想的模式和记忆容量有较严格的约束[42].基于SOINN的联想记忆系统[42, 43]希望能实现更加一般和通用的联想记忆,下面简要介绍文献[42]提出的一种基于SOINN的通用联想记忆系统(general associative memory,简称GAM).
GAM假设联想和记忆都是基于模式的,它可以完成由一种输入回忆起某种模式(自联想),或是由一种模式联想到一个或是多个其他的模式(异联想),这些模式可以为实值或者是二值的向量,同时记忆容量能不断增加.
如图 8所示,GAM采用3层结构,自下而上分别为:
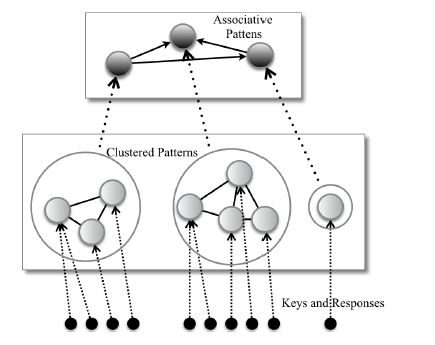
|
Fig. 8 Network structure of GAM 图 8 GAM的网络结构 |
1) 输入层:接受键(key)和响应(response)向量作为输入,其中,Key作为联想某个模式的线索模式,而Response则是希望能联想出的模式向量.这些输入都被视为不同的模式供第2层学习并记忆;
2) 记忆层:使用Adjusted SOINN算法对输入的模式进行学习,不同的模式对应于该层学习得到的不同的聚类;
3) 联想层:把记忆层学习到的每种模式都抽象为该层的一个节点,通过在该层建立不同节点间的有向连接来学习模式间的联想规则.联想规则可以是一对一、一对多、多对一或多对多,因此能够同时满足多种形式的联想记忆.
联想层为每次连接的起始节点分配一个索引来区别从一个节点发出的不同连接,这样就实现了一对多、多对多的联想规则.每个连接维护一个被激活次数的参数,该参数于每次使用该连接进行联想时增加一次.该值越高,表示该联想发生的可能性越大.因此,当一个输入模式有多个可能联想到的结果时,拥有最高值的联想规则会被首先返回.
GAM通过联想层的训练能够得到不同模式间的联想规则,实现了异联想.自联想主要由记忆层实现,因为记忆层的每个神经元都有一个因为SOINN的竞争过程而产生的Voronoi的区域,该区域被称为它的接收域(receptive field),所以任何的输入模式落入该区域都会被它所代表.因此在运行过程中,每个神经元的Voronoi的区域充当了记忆模式的吸引子(attractor)的角色,当原本的模式存在一定的偏差时,只要它仍然落在对应的接收域内就可以被恢复出来.
基于类似的思想,Shen等人设计了基于模式的推理算法[44].该算法以模式作为推理的命题对象(proposition),一组由若干命题对象的析取范式表示的If-Then规则作为输入来学习符合逻辑的推理规则.相似的If-Then规则得到的聚类簇被作为长期记忆(long term memory)储存起来,当一个待推理的命题到来时,找到学习结果中相似的推理规则进行递归地推理,直到存储的长期记忆中没有针对当前命题的推理规则.
3.4 密度估计密度估计的任务是从一组数据样本中恢复出生成该组样本的概率分布函数,在给定一个新的样本时,密度估计算法需要能够尽可能准确地返回这个样本点的概率密度.这样的密度信息对于异常检测和分类任务往往十分重要.传统的密度估计算法主要包括非参数式(nonparametric)方法和参数式(parametric)方法.非参数方法的代表是传统的核密度估计和一系列基于它的算法,它们的特点是几乎不需要任何假设就能提供理论上比较完备的密度估计结果.但它们通常受限于计算复杂度,只适合于处理低维和小数据样本.参数式方法假设数据服从某一特定的分布族,具有较强的概率假设,因此训练代价小,但也因此在应用上受到限制.
混合模型(finite mixture model)[45],其代表为高斯混合模型(Gaussian mixture model),是对参数式和非参数式模型的一种权衡.公式(12)使用一组加权的高斯分布来近似目标概率分布:
| $f(x)=\sum\limits_{n=1}^{K}{{{\alpha }_{n}}}\phi (x|{{\mu }_{n}},{{\Sigma }_{n}})$ | (12) |
其中,K为高斯成分的个数,an是第n个成分所占的权重,F(×)为高斯分布的概率密度函数.混合模型通常使用EM算法来进行学习,由于公式(12)的非凸性,算法一般收敛至局部最优点.此外,训练过程中K作为一个超参数,取值非常关键,通常需要反复运行算法比较BIC,AIC等指标才能确定合适的取值.
Nakamura[46, 47]使用SOINN训练好的神经元的权值作为高斯成分的均值,然后用使得该神经元成为获胜节点的所有局部数据样本计算该高斯成分的样本协方差矩阵.由于SOINN可以动态地增加删除神经元,因此该方法扩展了传统的成分数目固定的混合模型.但是由于协方差矩阵的计算需要用到所有的局部数据样本,该方法并不是完全在线的.Xiao等人[48]提出使用LB-SOINN的节点配合核密度估计算法进行密度,并分析了理想情况下的估计误差.Qiu等人[49]提出了一种名为LAIM的基于LD-SOINN的增量式高斯混合模型,每个神经元同样代表了高斯混合模型中的一个高斯成分,其中使用了一个特殊的阈值系统来控制高斯成分的生成.此外,LAIM使用了一个局部的更新策略,能够使用每个数据样本对其周围一部分的成分进行在线学习.这使得模型在降低训练复杂度的同时,能够发现局部变化较为复杂的密度分布.
3.5 流形学习流形学习的目的是恢复出高维数据中的低维流形结构.目前常见的流形学习算法有LLE[50],Isomap[51]等等,它们都试图使得数据从高维映射到低维空间时,高维数据间的邻域信息能够得到保留,即:原本相邻的点在低维空间也应该相邻;反之,在原始空间中距离较远的数据点在映射之后也要距离较远.这就是邻域保持(neighborhood preserving)的性质.
数据点之间的邻域关系是原始数据拓扑结构的局部性质,这些邻域关系包含了原始数据分布的拓扑结构信息,即:数据是以什么样的结构形式分布在特征空间中的,是各向同性(isotropic)的超球体、超平面还是其他不规则的流形结构.
SOINN以一组神经元来代表(或者说编码)原始数据,这实际上分别定义了两个映射关系,φ:MV和φ-1:VM,其中,M为嵌入在Rn中的数据流形,V为SOINN的节点集合.根据Martinetz等人[7]的定义,当映射φ和 φ-1同时满足邻域保持的性质时,图G(V,E)具有完美的拓扑保持性质(topology preserving).其中,E为神经元间的边集合.对φ来说,邻域保持就是指在数据流形中相邻的数据点被映射到在图G中相邻的神经元,对于φ-1也有类似的定义.已经证明:当任意的输入数据x及与其最相似的两个神经元w1,w2组成的三角形(x,w1,w2)完全位于数据流形中时(意味着神经元在流形上的分布足够稠密),CHL能够生成具有完美的拓扑保持性质以及路径保持性质的连接.TRN为此使用了NG作为分布神经元的算法,这需要预先指定神经元的数目并多次遍历训练样本.然而这种方式的优点在于可以把神经元的数量设置的足够多,以满足之前定义的稠密条件,使得最终的网络具有完美的拓扑保持性质;但相应地,这种方式也会使得网络不能适应新的输入环境,不具备增量学习的能力.
由于SOINN同样使用了CHL来建立神经元之间的连接,因此只要节点足够稠密,原始数据分布的拓扑结构也能完美地被SOINN的网络结构保留下来.Gan[52]基于此观察使用了SOINN自适应地为输入的高维数据生成land-mark点,改进了传统的流形学习算法Isomap,取得了更好的降维效果.Xiang等人[53]同时利用了GNG和SOINN来获得数据的拓扑表示,并使用神经元之间的相似度来代替原始数据间的距离,并以此提出了一个度量学习(metric learning)和低维嵌入(embbeding)的学习框架.
4 SOINN的应用SOINN已经在多个领域得到了应用,包括医疗专家系统、计算机视觉、异常检测、机器人智能等,以下是对这些工作的不完全总结.
· 医疗诊断和专家系统
Corchado等人[54, 55]将E-SOINN用于白血病的辅助诊断中,研究者们建立了一个混合专家系统(mixture expert system),包括数据的预处理、分类以及知识抽取这3个部分.E-SOINN被用于分类过程,其分类结果再通过CART[56]进行知识抽取,以辅助医生的诊断过程.
· 计算机视觉
Toyoda等人[57]将SOINN用于图像标记(image labeling).首先,从像素矩阵中分别抽取出图像的纹理和颜色特征;然后,把属于相同类别的特征送入SOINN进行聚类,学习到的SOINN节点用于代表该类的颜色特征和纹理特征.Kawewong等人[58]把SOINN用于室内场景识别.Sun等人把ESOINN中的距离度量替换为Mahalanobis距离,然后使用修改后的ESOINN来匹配摄像头中不同图像帧中的相同人物[59].袁飞云等人使用了SOINN对图像进行分类[79].此外,SOINN在目标物体识别也有相关的应用[60, 61].Yang等人基于SOINN提出了改进的ViSOINN[62]提取图像中的子图来进行图像分类.
· 异常检测
Xiang等人[63]用一种半监督学习的方法配合E-SOINN建立了一个入侵检测系统,在KDD Cup 99数据集上取得了较好的效果.Carpine等人[64]把SOINN用于IRC(internet relay channel)僵尸网络(botnets)的在线检测.
· 机器人智能
He等人[65]使用SOINN作为一个人形机器人的学习系统,通过图像展示以及语音指导等多模态的训练过程,使得机器人能够用一些简单的自然语言来描述当前的物理场景,同时还能与人进行简单的词汇交流.He和其他研究者们还利用来自语音和视觉的信息,使用SOINN训练机器人理解单词的含义[66].Kawewong[67]和Tangruamsub[68]把基于SOINN的联想记忆系统分别用于机器人路径规划(path-planning)和导航(navigation). Okada 等人[69, 70, 71]使用SOINN实现了机器人的手势识别.Najjar等人[72]使用SOINN来学习机器人传感器输入与电机响应之间的关联,从而使得机器人学习一些特定的关节动作来执行制定的任务.
除上述常见的应用领域外,Chen等人[73]把SOINN用于GPU加速的并行在线聚类过程;Noorbehbahani等
人[74]修改了Ajusted SOINN的距离度量来进行在线聚类;Ranvier等人[75]使用ESOINN来帮助重构用户使用移动设备时的复杂流程,这些流程可以被用于分析用户的活动情况;时晓峰等人探讨了基于SOINN的信息融合技术[78];Hasegawa等研究人员将SOINN应用在机器人上,经过一段时间的训练,当研究人员要求它把一杯水进行降温时,它主动做出了使用冰块降温的动作,而这个动作是没有作为程序写在机器人芯片内部的,这表明SOINN使得机器人面对不断变化的外界环境,具有了一定的自主性与学习能力.
总的来看,机器人智能是SOINN最主要的应用方向.这是由于SOINN增量学习的能力非常适合用于机器人智能的训练过程,自适应的学习算法不需要太多人的干预.不需要指定聚类的数目,使得SOINN适合于在没有先验知识的情况下,得到数据的大致密度分布以及拓扑结构的信息.
5 未来的研究方向虽然在实际应用中取得了不错的结果,但是SOINN还有一些理论上的工作有待完善,以下是一些值得研究和探讨的问题.
1) 缺乏严格的理论证明:固定神经元数量的竞争型神经网络在理论上往往较容易分析,如SOM,NG算法均有不同程度的收敛性以及密度近似的分析结果.然而没有固定结构的增量式算法如GNG,GHSOM[76],SOINN进行理论分析则较为困难,目前并没有关于它们的严格数学分析.因此,如何从理论上分析这类结构随时间变化的竞争型神经网络的收敛性质,是未来的一个研究重点;
2) 对数据输入次序敏感:基于在线学习的竞争型神经网络有一个普遍的问题就是对数据的输入次序非常敏感,一个好的输入次序和不好的输入次序会导致网络的性能千差万别.LB-SOINN已经尝试使用负载平衡的方式来缓解这个问题,然而这引入了许多自定义的参数,提高了算法使用时的复杂性.如何找出更简单有效的方式来解决这一问题,具有十分重大的意义.
6 结束语SOINN是一种能够对数据进行在线聚类和拓扑表示的竞争神经网络,目前已经在多个领域中得到了应用. Araujo等人[77]把SOINN归类为一种网络结构随时间变化的自组织映射网(self-organizing maps with time- varying structure),我们认为,它的特点不仅体现于结构的自组织性上,更重要的是它增量学习的能力,能够学习新的输入模式而不影响之前学习的结果.本文介绍了SOINN的基本思想、一般性质以及典型的应用,希望通过这些,能够使读者对SOINN有一个较为全面的了解,并在有需要的情况下,将其应用到科研工作的相关问题中.
| [1] | Shen F, Hasegawa O. An incremental network for on-line unsupervised classification and topology learning. Neural Networks, 2006, 19 (1) :90–106. [doi:10.1016/j.neunet.2005.04.006] |
| [2] | Shen F, Ogura T, Hasegawa O. An enhanced self-organizing incremental neural network for online unsupervised learning. Neural Networks, 2007, 20 (8) :893–903. [doi:10.1016/j.neunet.2007.07.008] |
| [3] | Shen F, Hasegawa O. elf-Organizing incremental neural network and its application.In:Proc.of the Int'l Conf.on Artificial Neural Networks (ICANN 2010).. Berlin,Heidelberg:Springer-Verlag, 2010 :535–540. [doi:10.1007/978-3-642-15825-4_74] |
| [4] | Kohonen T. The self-organizing map. Proc.of the IEEE, 1990, 78 (9) :1464–1480. [doi:10.1109/5.58325] |
| [5] | Kohonen T. Self-Organized formation of topologically correct feature maps. Biological Cybernetics, 1982, 43 (1) :59–69. [doi:10.1007/BF00337288] |
| [6] | Martinetz TM, Berkovich SG, Schulten KJ. Neural-Gas network for vector quantization and its application to time-series prediction. IEEE Trans.on Neural Networks, 1993, 4 (4) :558–569. [doi:10.1109/72.238311] |
| [7] | Martinetz TM, Schulten KJ. Topology representing networks. Neural Networks, 1994, 7 (3) :507–522. [doi:10.1016/0893-6080(94)90109-0] |
| [8] | Carpenter GA, Grossberg S. The ART of adaptive pattern recognition by a self-organizing neural network. Computer, 1988, 21 (3) :77–88. [doi:10.1109/2.33] |
| [9] | Sun DW, Zhang GY, Zheng WM. Big data stream computing:Technologies and instances. Ruan Jian Xue Bao/Journal of Software, 2014, 25 (4) :839–862(in Chinese with English abstract). [doi:10.13328/j.cnki.jos.004558] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4558&journal_id=jos |
| [10] | Sun GJ, Liu J, Zhao LY. Clustering algorithms research. Ruan Jian Xue Bao/Journal of Software, 2008, 19 (1) :48–61(in Chinese with English abstract). [doi:10.3724/SP.J.1001.2008.00048] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20080106&journal_id=jos |
| [11] | MacQueen J. Some methods for classification and analysis of multivariate observations.In:Lucien M,ed.Proc.of the 5th Berkeley Symp.on Mathematical Statistics and Probability.. London:University of California Press, 1967 :281–297. |
| [12] | Bezdek JC.Pattern Recognition with Fuzzy Objective Function Algorithms.New York:Plenum Press,1981.[doi:10.1007/978-1-4757-0450-1] |
| [13] | Dunn JC. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. Cybernet, 1973, 3 (3) :32–57. [doi:10.1080/01969727308546046] |
| [14] | Steinbach M,Karypis G,Kumar V.A comparison of document clustering techniques.In:Proc.of the KDD Workshop on Text Mining.2000. |
| [15] | Kaufman L,Rousseeuw PJ.Finding Groups in Data:An Introduction to Cluster Analysis.New Jersey:John Wiley&Sons,2009. |
| [16] | Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 1977, 39 (1) :1–38. http://cn.bing.com/academic/profile?id=1485632300&encoded=0&v=paper_preview&mkt=zh-cn |
| [17] | Ng AY, Jordan MI, Weiss Y. On spectral clustering:Analysis and an algorithm. In:Proc.of the Advances in Neural Information Processing Systems., 2002 :849–856. http://cn.bing.com/academic/profile?id=2165874743&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] | Carpenter GA, Grossberg S. ART 2:Self-Organization of stable category recognition codes for analog input patterns. Applied Optics, 1987, 26 (23) :4919–4930. [doi:10.1364/AO.26.004919] |
| [19] | Carpenter GA, Grossberg S. ART 3:Hierarchical search using chemical transmitters in self-organizing pattern recognition architectures. Neural Networks, 1990, 3 (2) :129–152. [doi:10.1016/0893-6080(90)90085-Y] |
| [20] | Fritzke B. Growing cell structures-A self-organizing network for unsupervised and supervised learning. Neural Networks, 1994, 7 (9) :1441–1460. [doi:10.1016/0893-6080(94)90091-4] |
| [21] | Fritzke B. A growing neural gas network learns topologies. In:Proc.of the Advances in Neural Information Processing Systems, 1995 :625–632. http://cn.bing.com/academic/profile?id=2138754805&encoded=0&v=paper_preview&mkt=zh-cn |
| [22] | Gray RM. Vector quantization. IEEE ASSP Magazine, 1984, 1 (2) :4–29. [doi:10.1109/MASSP.1984.1162229] |
| [23] | Lloyd S. Least squares quantization in PCM. on Information Theory, 1982, 28 (2) :129–137. [doi:10.1109/TIT.1982.1056489] |
| [24] | Max J. Quantizing for minimum distortion. IRE Trans.on Information Theor, 1960, 6 (1) :7–12. [doi:10.1109/TIT.1960.1057548] |
| [25] | Linde Y, Buzo A, Gray RM. An algorithm for vector quantizer design. IEEE Trans.on Communications, 1980, 28 (1) :84–95. [doi:10.1109/TCOM.1980.1094577] |
| [26] | Robbins H, Monro S. A stochastic approximation method. In:Proc.of the Annals of Mathematical Statistics, 1951 :400–407. [doi:10.1214/aoms/1177729586] |
| [27] | Zador P. Asymptotic quantization error of continuous signals and the quantization dimension. IEEE Trans.on Information Theory, 1982, 28 (2) :139–149. [doi:10.1109/TIT.1982.1056490] |
| [28] | Villmann T, Claussen JC. Magnification control in self-organizing maps and neural gas. Neural Computation, 2006, 18 (2) :446–469. [doi:10.1162/089976606775093918] |
| [29] | Duda RO,Hart PE,Stork DG.Pattern Classification.2nd ed.,New York:John Wiley&Sons,2012. |
| [30] | Zhang H, Xiao X, Hasegawa O. A load-balancing self-organizing incremental neural network. IEEE Trans.on Neural Networks and Learning Systems, 2014, 25 (6) :1096–1105. [doi:10.1109/TNNLS.2013.2287884] |
| [31] | Shen F, Hasegawa O. A fast nearest neighbor classifier based on self-organizing incremental neural network. Neural Networks, 2008, 21 (10) :1537–1547. [doi:10.1016/j.neunet.2008.07.001] |
| [32] | Ouyang Q, Shen F, Zhao J. A local distribution net for data clustering.In:Patricia A,ed.Proc.of the Pacific Rim Int'l Conf.on Artificial Intelligence (PRICAI). Berlin,Heidelberg:Springer-Verlag, 2012 :411–422. [doi:10.1007/978-3-642-32695-0_37] |
| [33] | Xing YL, Cao TY, Zhou K, Shen FR, Zhao JX. An incremental local distribution network for unsupervised learning.In:Cao T,ed.Proc.of the Advances in Knowledge Discovery and Data Mining. Ho Chi Minh:Springer Int'l Publishing, 2015 :646–658. [doi:10.1007/978-3-319-18038-0_50] |
| [35] | Kohonen T. Improved versions of learning vector quantization. In:Proc.of the Int'l Joint Conf.on Neural Networks (IJCNN).San Diego:IEEE, 1990 :545–550. [doi:10.1109/IJCNN.1990.137622] |
| [36] | Wilson DL. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans.on Systems,Man and Cybernetics, 1972, 3 :408–421. [doi:10.1109/TSMC.1972.4309137] |
| [37] | Xu Y, Shen F, Hasegawa O, Zhao J. An online incremental learning vector quantization. In:Proc.of the Advances in Knowledge Discovery and Data Mining.Berlin,Heidelberg:Springer-Verlag, 2009 :1046–1053. [doi:10.1007/978-3-642-01307-2_112] |
| [38] | Zheng J, Shen F, Fan H, Zhao J. An online incremental learning support vector machine for large-scale data. Neural Computing and Applications, 2013, 22 (5) :1023–1035. [doi:10.1007/s00521-011-0793-1] |
| [39] | Shen F, Sakurai K, Kamiya Y. An online semi-supervised active learning algorithm with self-organizing incremental neural network. In:Proc.of the Int'l Joint Conf.on Neural Networks (IJCNN).Orlando:IEEE, 2007 :1139–1144. [doi:10.1109/IJCNN.2007.4371118] |
| [40] | Kamiya Y, Ishii T, Shen F. An online semi-supervised clustering algorithm based on a self-organizing incremental neural network. In:Proc.of the Int'l Joint Conf.on Neural Networks (IJCNN).Orlando:IEEE, 2007 :1061–1066. [doi:10.1109/IJCNN.2007.4371105] |
| [41] | Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc.of the National Academy of Sciences, 1982, 79 (8) :2554–2558. [doi:10.1073/pnas.79.8.2554] |
| [42] | Shen F, Ouyang Q, Kasai W. A general associative memory based on self-organizing incremental neural network. Neurocomputing, 2013, 104 :57–71. [doi:10.1016/j.neucom.2012.10.003] |
| [43] | Sudo A, Sato A, Hasegawa O. Associative memory for online learning in noisy environments using self-organizing incremental neural network. IEEE Trans.on Neural Networks, 2009, 20 (6) :964–972. [doi:10.1109/TNN.2009.2014374] |
| [44] | Shen F, Sudo A, Hasegawa O. An online incremental learning pattern-based reasoning system. Neural Networks, 2010, 23 (1) :135–143. [doi:10.1016/j.neunet.2009.06.002] |
| [45] | MacLachlan GJ,Peel D.Finite Mixture Models.New York:John Wiley&Sons,2000. |
| [46] | Nakamura Y, Hasegawa O. Robust fast online multivariate non-parametric density estimator. .In:Proc.of the Int'l Conf.on Neural Information Processing.Berlin,Heidelberg:Springer-Verlag, 2013 :180–187. [doi:10.1007/978-3-642-42042-9_23] |
| [47] | Yoshihiro N,Hasegawa O.Nonparametric density estimation based on self-organizing incremental neural network for large noisy data.IEEE Trans.on Neural Networks and Learning Systems,2016.[doi:10.1109/TNNLS.2015.2489225] |
| [48] | Xiong X,Zhang H,Hasegawa O.Density estimation method based on self-organizing incremental neural networks and error estimation.In:Proc.of the Int'l Conf.on Neural Information Processing.Berlin,Heidelberg:Springer-Verlag,2013. |
| [49] | Qiu T, Shen F, Zhao J. Local adaptive and incremental gaussian mixture for online density estimation. .In:Proc.of the Advances in Knowledge Discovery and Data Mining.Ho Chi Minh City:Springer Int'l Publishing, 2015 :418–428. [doi:10.1007/978-3-319-18038-0_33] |
| [50] | Roweis ST, Lawrence KS. Nonlinear dimensionality reduction by locally linear embedding. Science, 2000, 290 (5500) :2323–2326. [doi:10.1126/science.290.5500.2323] |
| [51] | Tenenbaum JB, Silva VD, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science, 2000, 290 (5500) :2319–2323. [doi:10.1126/science.290.5500.2319] |
| [52] | Gan Q, Shen F, Zhao J. An extended isomap for manifold topology learning with SOINN landmarks. .In:Proc.of the 22nd Int'l Conf.on Pattern Recognition (ICPR).Stockholm:IEEE, 2014 :1579–1584. [doi:10.1109/ICPR.2014.280] |
| [53] | Xiang Z, Zhu X, Dong W. A framework for metric learning and embedding with topology learning neural networks. In:Proc.of the Int'l Conf.on Natural Computation (ICNC).Zhangjiajie:IEEE, 2015 :118–112. [doi:10.1109/ICNC.2015.7377976] |
| [54] | Corchado JM, De Paz JF, Rodríguez S. Model of experts for decision support in the diagnosis of leukemia patients. Artificial Intelligence in Medicine, 2009, 46 (3) :179–200. [doi:10.1016/j.artmed.2008.12.001] |
| [55] | De Paz JF, Rodríguez S, Bajo J. Case-Based reasoning as a decision support system for cancer diagnosis:A case study. Int'l Journal of Hybrid Intelligent Systems, 2009, 6 (2) :97–110. [doi:10.3233/HIS-2009-0089] |
| [56] | Loh WY. Classification and regression trees. Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery, 2011, 1 (1) :14–23. [doi:10.1002/widm.8] |
| [57] | Toyoda T, Tagami K, Hasegawa O. Integration of top-down and bottom-up information for image labeling. In:Proc.of the IEEE Computer Society Conf.on Computer Vision and Pattern Recognition.New York:IEEE, 2006 :1106–1113. [doi:10.1109/CVPR.2006.156] |
| [58] | Kawewong A,Pimpup R,Hasegawa O.Incremental learning framework for indoor scene recognition.In:Proc.of the 27th AAAI Conf.on Artificial Intelligence.2013. |
| [59] | Sun Y, Liu H, Sun Q. Online learning on incremental distance metric for person re-identification. In:Proc.of the IEEE Int'l Conf.on Robotics and Biomimetics (ROBIO).Bali:IEEE, 2014 :1421–1426. [doi:10.1109/ROBIO.2014.7090533] |
| [60] | Kankuekul P, Kawewong A, Tangruamsub S. Online incremental attribute-based zero-shot learning. In:Proc.of the IEEE Conf.on Computer Vision and Pattern Recognition (CVPR).Providence:IEEE, 2012 (3657) :3664. [doi:10.1109/CVPR.2012.6248112] |
| [61] | Kawewong A, Hasegawa O. Fast and incremental attribute transferring and classifying system for detecting unseen object classes. In:Proc.of the Int'l Conf.on Artificial Neral Networks (ICANN).Berlin,Heidelberg:Springer-Verlag, 2010 :563–568. [doi:10.1007/978-3-642-15825-4_78] |
| [62] | Yang YB, Li YN, Gao Y, Yin H, Tang Y. Structurally enhanced incremental neural learning for image classification with subgraph extraction. Int'l Journal of Neural Systems, 2014, 24 (7) :1450024. [doi:10.1142/S0129065714500245] |
| [63] | Xiang Z, Zhu J, Han W. On the capability of SOINN based intrusion detection systems. Journal of Computational Information Systems, 2013, 9 (3) :941–949. |
| [64] | Carpine F, Mazzariello C, Sansone C. Online IRC botnet detection using a SOINN classifier. In:Proc.of the IEEE Int'l Conf.on Communications (ICC).Budapest:IEEE, 2013 :1351–1356. [doi:10.1109/ICCW.2013.6649447] |
| [65] | He X, Ogura T, Satou A, Hasegawa O. Developmental word acquisition and grammar learning by humanoid robots through a self-organizing incremental neural network. IEEE Trans.on Systems,Man,and Cybernetics, 2007, 37 (5) :1357–1372. [doi:10.1109/TSMCB.2007.903447] |
| [66] | He X, Kojima R, Hasegawa O. Developmental word grounding through a growing neural network with a humanoid robot. IEEE Trans.on Systems,Man,and Cybernetics, 2007, 37 (2) :451–462. [doi:10.1109/TSMCB.2006.885309] |
| [67] | Kawewong A, Honda Y, Tsuboyama M. Reasoning on the self-organizing incremental associative memory for online robot path planning. IEICE Trans.on Information and System, 2010, 93 (3) :569–582. [doi:10.1587/transinf.E93.D.569] |
| [68] | Tangruamsub S, Ka Wewong A, Tsuboyama M, Hasegawa O. Self-Organizing incremental associative memory-based robot navigation. IEICE Trans.on Information and Systems, 2012, 95 (10) :2415–2425. [doi:10.1587/transinf.E95.D.2415] |
| [69] | Okada S, Kobayashi Y, Ishibashi S, Nishida T. Incremental learning of gestures for human-robot interaction. AI&Society, 2010, 25 (2) :155–168. [doi:10.1007/s00146-009-0248-8] |
| [70] | Okada S, Nishida T. Incremental clustering of gesture patterns based on a self organizing incremental neural network. In:Proc.of the Int'l Joint Conf.on Neural Networks.Atlanta:IEEE, 2009 :2316–2322. [doi:10.1109/IJCNN.2009.5178845] |
| [71] | Okada S, Hasegawa O. Motion recognition based on dynamic-time warping method with self-organizing incremental neural network. In:Proc.of the Int'l Conf.on Pattern Recognition.Tampa:IEEE, 2008 :1–4. [doi:10.1109/ICPR.2008.4761483] |
| [72] | Tarek N, Hasegawa O. Self-Organizing incremental neural network (SOINN) as a mechanism for motor babbling and sensory-motor learning in developmental robotics. Puerto de la Berlin,Heidelberg:Springer-Verlag, 2013 :321–330. [doi:10.1007/978-3-642-38679-4_31] |
| [73] | Chen C, Mu D, Zhang H, Hu W. Towards a moderate-granularity incremental clustering algorithm for GPU. .In:Proc.of the Int'l Conf.on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC).Beijing:IEEE, 2013 :194–201. [doi:10.1109/CyberC.2013.38] |
| [74] | Noorbehbahani F, Mousavi SR, Mirzaei A. An incremental mixed data clustering method using a new distance measure. Soft Computing, 2015, 19 (3) :731–743. [doi:10.1007/s00500-014-1296-7] |
| [75] | Ranvier JE,Catasta M,Vasirani M,Aberer K.RoutineSense:A mobile sensing framework for the reconstruction of user routines.In:Proc.of the 12th Int'l Conf.on Mobile and Ubiquitous Systems:Computing,Networking and Services.Coimbra,2015.EPFL-CONF-208793.[doi:10.4108/eai.22-7-2015.2260055] |
| [76] | Rauber A, Merkl D, Dittenbach M. The growing hierarchical self-organizing map:Exploratory analysis of high-dimensional data. IEEE Trans.on Neural Networks, 2002, 13 (6) :1331–1341. [doi:10.1109/TNN.2002.804221] |
| [77] | Araujo AFR, Rego RLME. Self-Organizing maps with a time-varying structure. ACM Computing Surveys (CSUR), 2013, 46 (1) :7. [doi:10.1145/2522968.2522975] |
| [78] | Shi XF, Shen FR, He HW. Information fusion based on self-organizing incremental neural network (in Chinese with English abstract). Ordnance Industry Automation, 2015, 34 (5) :59–65(in Chinese with English abstract). [doi:10.7690/bgzdh.2015.05.016] |
| [79] | Yuan FY. Codebook generation based on self-organizing incremental neural network for image classification (in Chinese with English abstract). Journal of Computer Applications, 2013, 33 (7) :1976–1979(in Chinese with English abstract). [doi:10.11772/j.issn.1001-9081.2013.07.1976] |
| [9] | 孙大为, 张广艳, 郑纬民. 大数据流式计算:关键技术及系统实例. 软件学报, 2014,25 (4) :839–862. [doi:10.13328/j.cnki.jos.004558] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=4558&journal_id=jos |
| [10] | 孙吉贵, 刘杰, 赵连宇. 聚类算法研究. 软件学报, 2008,19 (1) :48–61. [doi:10.3724/SP.J.1001.2008.00048] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=20080106&journal_id=jos |
| [34] | 山崎和博, 巻渕有哉, ShenFR, 申富饶, 长谷川修. 自己増殖型ニューラルネットワーク SOINN とその実践. The Brain&Neural Networks, 2010,17 (4) :187–196. [doi:10.3902/jnns.17.187] |
| [78] | 时晓峰, 申富饶, 贺红卫. 基于自组织增量学习神经网络的信息融合技术. 兵工自动化, 2015,34 (5) :59–65. [doi:10.7690/bgzdh.2015.05.016] |
| [79] | 袁飞云. 基于自组织增量神经网络的码书产生方法在图像分类中的应用. 计算机应用, 2013,33 (7) :1976–1979. [doi:10.11772/j.issn.1001-9081.2013.07.1976] |
 2016, Vol. 27
2016, Vol. 27



