许多现实应用中,图数据的规模都在不断地增大,Facebook在2014年公布其月活跃用户人数(顶点数)达到12.6亿,好友关系(边数)达到1 400亿,用户数据信息超过300PB.在这样规模的图上做查询,将是非常耗时的[1].
在现实应用中,社团查询是一种非常普遍的操作.比如:在社交网络中,查询联系紧密的社团可以帮助挖掘用户的社会行为[2];在作者合作网络中,一群联系密切的人可能具有相近的研究领域[3];在购物数据中,一组关系密切的商品很可能被兴趣相近的客户所关注[4];在蛋白质网络中,一些关系紧密的蛋白质往往可能共同形成特定的官能团[5].
目前,对于紧密社团[6]的定义有许多种,如:团、k团、g准团、k丛等.上述问题均是NP-hard的,故计算以上的紧密社团将非常耗时.而k核作为一种社团的定义,则可以被有效地在线性时间内计算.对于无向图G=(V,E),k核是图G的一个极大子图,满足子图内的顶点都至少有k个邻居出现在子图中.例如在图 1(a)中,{8,9,11,12,14}的导出子图就是一个3核,因为每个顶点在导出子图中都至少有3个邻居.作为一种紧密社团,k核有着广泛的应用:k核可以作为一种拓扑结构信息用于网络分析[7]和网络可视化[8];k-1核还可以用于近似表示k团;k核还可以用于给出最稠密子图的1/2近似[9]以及最稠密至少k子图的1/3近似算法[10].
事实上,在很多应用中,用户往往更加关心包含一组给定查询顶点Q的连通的k核.由于满足上述要求的k核并不唯一,而其中最稠密的往往最有意义,故本文所关注的是包含给定查询顶点集Q且具有最大k值的连通k核,简称为k-MSC.仍以图 1(a)为例,若给定查询顶点集Q={4,8,15},那么包含Q的k-MSC为g1,是一个2核.

|
(a) 原始图G (b) 压缩图GC (c) 压缩树GT Fig. 1 Instances of graph compression 图 1 图压缩实例 |
本文首先提出了k-MSC问题,而现有方法并不能有效地解决k-MSC问题.这是因为:(1) 枚举包含Q的所有导出子图,并找到其中k值最大的连通k核,将访问指数级别数量的子图,故并不可行;(2) 借助于现有计算k核的最快算法[11],一种直观的算法(Base)可以通过不断递减k的值,然后检查是否存在一个连通的k核包含了Q中的全部顶点.为保证连通性,上述过程每次都需要遍历整个图,当原始图规模很大时,该计算将变得非常耗时.
本文使用图压缩以及压缩图上直接进行查询处理的技术来解决k-MSC问题.其思想是:首先将图G进行压缩,得到一个规模很小的压缩图GC;然后,对于任意G上的k-MSC查询(G,Q),将其转换成GC上的等价查询(GC,QC),使得G上对Q的查询结果与GC上对QC的查询结果完全相同.由于GC的规模远小于G,故可以大幅提高查询处理效率,并节省存储空间.
文献[12, 13, 14]中的图压缩技术将图中的邻接信息用bit表示,并通过适当的合并、调整顺序等操作令所使用的bit数最少,从而使得其对网络图和社交网络的压缩效果非常可观.然而上述方法仅仅关注了存储代价的降低而忽视了查询效率,这导致压缩图并不能直接被使用,即使是最简单的邻居查询,也需要将压缩图进行适当的解压缩才能够进行查询.除了上述通用的图压缩技术,一些针对特定查询的图压缩技术也被提出[15, 16, 17, 18].文献[15]提出了针对可达查询和图模拟查询的图压缩技术;文献[16]探讨了在XML树中能够处理XPath查询的压缩方法;文 献[17]针对邻居查询,提出了具有误差保证的有损压缩技术.然而,由于查询结构的差异,上述方法就不能适用于k-MSC查询.
本文首先提出了图压缩算法SC,其时间复杂度为O(|E|).SC算法是基于等价类划分的,故查询转换的时间复杂度为O(|Q|).本文证明了基于压缩图GC的查询正确性.通过实验验证,SC算法可以有效地将原始图压缩掉一半以上;且对于稠密图,压缩效果将进一步提升,达到压缩掉近70%.对于道路交通网络和基于偏好模型的虚拟图,SC算法可将原始图压缩掉近90%.
由于k-MSC查询仅需要找到符合要求的连通区域,故SC算法得到的压缩图GC还可被进一步压缩.本文提出了图压缩算法TC,将压缩图GC进一步压缩为树GT,其时间复杂度为O(|VC|+|EC|).本文证明了基于压缩图GT的查询的正确性,并提出了压缩树上无需解压缩的查询算法QueryGT,其时间复杂度为O(|RQ|).其中,|RQ|为查询结果集的大小.通过实验验证:在真实数据集上,TC算法可进一步将SC算法的压缩比提升3~5倍.与直接在原始图上查询的Base算法相比,基于压缩树的查询算法QueryGT的查询效率将提升1~2个数量级.
本文的主要工作及贡献如下.
(1) 提出了一种支持k-MSC查询的图压缩算法SC以及相应的查询转换算法,证明了其正确性,SC算法的时间复杂度为O(|E|);
(2) 在SC算法的基础上,提出了图压缩算法TC,将压缩图进一步压缩为树,证明了压缩树上查询结果的正确性,TC算法的时间复杂度为O(|VC|+|EC|);
(3) 提出了压缩树上的查询算法,其时间复杂度为O(|RQ|);
(4) 分别在真实数据和虚拟数据上验证了所提出图压缩算法的有效性.真实数据集上的实验结果表明:压缩算法的压缩比可达到12%;而对于稠密图,算法将取得更好的接近10%的压缩比.算法对于虚拟数据集同样有效,平均压缩比仍然在12%左右;且压缩效果随着图稠密度的增加而提高.对平均度数为30的虚拟图,压缩比为6.7%.基于压缩算法的查询算法效率也得到了很好的提升,无论在真实还是虚拟数据集上,查询效率与Base算法相比均提高了1~2个数量级.
1 相关工作网络图和社交网络的通用图压缩技术已经被广泛研究,文献[12]的压缩技术能够有效地将网络图压缩,文献[13, 14]也可以将社交网络以bit的形式有效存储.由于上述技术保存了原始图中全部的结构信息,即,并不针对特定查询,且查询前必须进行解压缩操作,故反而降低了查询效率.
面对特定查询且无需解压缩即可查询的图压缩技术也被提出:文献[15]提出了能够处理可达查询和图模拟查询的图压缩技术,文献[16]利用了双向模拟的思想提出了针对XPath查询的压缩技术,文献[17]则针对邻居查询给出了一种具有误差保证的有损压缩技术.然而上述技术仅能处理特定的查询,因此无法适用于k-MSC查询.
对于给定图和一组查询顶点Q,围绕如何找到图中包含Q的社团也展开了一些研究[18, 19, 20, 21].其中,文献[18]提出了一种基于局部模块化的社团计算方法,文献[19]定义了基于k-truss的社团并给出了求解算法,文献[20]研究了基于g准团定义的社团发现问题.由于对社团定义的差别,上述技术无法适用于k-MSC查询.文献[21]研究了基于连通度定义的最大连通社团发现问题,并提出了SMCC索引提高查询性能.本文将以SMCC索引作为对比,说明SC和TC算法的有效性.
2 最大Steiner连通k核本文针对简单的无向无权图进行研究,即对于给定图G=(V,E),V是顶点集,E是边集,那么图中不存在自环(u,u),其中,u∈V.本文使用的图数据是以邻接表形式存储的,因此,图的规模|G|为邻接表中邻接顶点对的数量.对于顶点u∈V,v∈V,(u,v)和(v,u)表示同一条边,而由于(u,v)和(v ,u)分别在顶点u和v的邻接表中各出现一次,故图的规模|G|=2|E|.
对于图G中的任意的顶点集H,G[H]表示H的导出子图,即G[H]=(H,{(u,v)∈E|u,v∈H}).记图G中连接顶点u和v的简单路径为P(G,u,v),则P(G,u,v)={u,w1,w2,…,wt,v},其中,(u,w1)∈E,(wt,v)∈E,(wi,wi+1)∈E,0<i<t,当G明确时,P(G,u,v)简记为P(u,v).
定义1. 给定图G=(V,E),k核是满足以下性质的子图G[H]:(1) H⊆V;(2) 对于顶点u∈H,u在G[H]中至少有k个邻居;(3) G[H]是极大的,即,不存在H',满足H⊆H'⊆V且G[H']是k核.
定义2. 给定图G=(V,E),对于顶点u∈V,u的核值core(u)为u所在全部k核中的最大值,即:
core(u)=MaxH⊆V{k|u∈H且G[H]为k核}.
例如,在图 1(a)中,由H={8,9,11,12,14}生成的导出子图中每个顶点的核值均为3,因为它们在G[H]中的度均为3且图中不存在一个4核.但是G[H]并不是3核,因为图中存在着一个更大的3核G[H'],其中H'={8,9,11,12,14,15,16,17,18}.值得注意的是,k核并不一定是连通的.
定义3. 给定图G=(V,E),查询顶点集Q,包含Q的Steiner连通k核是满足以下性质的子图G[H]:(1) Q⊆H⊆V且G[H]是连通的;(2) 对于顶点u∈H,u在G[H]中至少有k个邻居;(3) G[H]是极大的,即,不存在H',满足H⊆H'⊆V且G[H']是Steiner连通k核.本文简称Steiner连通k核为k-SC.
定义4. 给定图G=(V,E),查询顶点集Q,包含Q的最大Steiner连通k核是核值最大的k-SC,简称为k-MSC,记此最大核值为MSC(G,Q).当G明确时,MSC(G,Q)可简记为MSC(Q).
仍然以图 1(a)为例,若Q={8},则存在一个3-SC,G[{8,9,11,12,14}],一个2-SC,G[V \{1,2,3,10}]和一个1-SC,G[V].根据定义4可知:包含{8}的k-MSC为G[{8,9,11,12,14}],而MSC({8})=3.
事实上,当|Q|=1,即,查询顶点集只包含一个顶点时,记Q中顶点为u,则MSC(Q)=core(u),包含Q的k-MSC为core(u)核中包含u的极大连通子图.仍以Q={8}为例,显然,MSC({8})=core(8)=3成立.而由于图中的3核为G[{8,9,11,12,14,15,16,17,18}],故包含{8}的极大连通子图为G[{8,9,11,12,14}],G[{8,9,11,12,14}]也是包含{8}的k-MSC.
由于k-SC和k-MSC均为导出子图,故在不引起歧义时,可以将k-SC和k-MSC看作顶点集H.在下文中,将交替使用H和G[H]表示k-SC和k-MSC的查询结果.另外,由于计算包含Q的k-MSC和MSC(Q的过程非常相近,且计算前者需要额外的步骤,故本文仅讨论前种查询.
下面给出G的顶点集V上等价关系“≡”的定义.
定义5. 给定图G=(V,E),“≡”是V上的二元关系,对于顶点u∈V,v∈V,u≡v当且仅当图G中存在一条简单路径P(u,v),使得对于任意顶点w∈P(u,v),core(w)=core(u)=core(v).
由于任意顶点均与自身连通,故u≡u.易知,关系“≡”满足自反性、对称性和传递性.所以,关系“≡”是V上的等价关系.可以根据“≡”将V划分为若干个等价类,[u]C={v|v∈V,u≡v}表示包含顶点u的等价类,若顶点v与等价类
[u]C中任意顶点u等价,则称v属于[u]C,记作v$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\square }$[u]C.
2.1 图压缩算法SC本文首先给出第1种图压缩方法SC:将图G中的顶点划分为若干个等价类,每个等价类都是压缩图GC= (VC,EC,f)中的一个顶点;压缩图GC中两个顶点[u]C和[v]C之间存在一条边([u]C,[v]C)当且仅当在原始图G中存在两个顶点u∈[u]C和v∈[v]C,满足(u,v)∈E.f是顶点集上VC的权值函数,记录了该顶点对应的原始图顶点的核值.算法1给出了SC算法的执行过程.关于算法1的具体细节和复杂度分析,将在第2.2节介绍.
在将图G压缩为GC后,可以在压缩图GC上直接查询.对于任意给定查询顶点集Q,QC={v|uv,u∈Q}是压缩
图上与Q对应的查询顶点集,即,Q中顶点所在等价类的集合.为了计算图G中包含Q的k-MSC,可以通过计算GC中包含QC的k-MSC作为查询结果.
例如在对图 1(a)中的原始图G进行压缩时,因为顶点1,2,3核值均为1且可以通过路径P(1,3)={1,2,3}连接,所以合并1,2,3得到u1且f(u1)=1,如图 1(b)所示(u1={1,2,3},u2={4,5,6,7},u3={8,9,11,12,14},u4={13},u5={15,16,17,18},u6={10}),类似地,顶点4,5,6,7可合并为u2且f(u2)=2,8,9,11,12,14可合并为u3且f(u3)=3,15,6,17,18可合并为u5且f(u5)=3,至此可得到图 1(b)中的压缩图GC.而对于给定查询“包含{8,12,15}的k-MSC”,只需计算压缩图GC中包含{u3,u5}的k-MSC即可,而包含{u3,u5}的k-MSC为GC[{u2,u3,u4,u5}],这与原始图G上的查询结果是相同的.
以下定理将证明在压缩图GC上计算的k-MSC的是正确的.
引理1. 在图G=(V,E)中,若(u,v)∈E且core(u)=core(v),则对于图G中任意一个最大Steiner连通k核G[H],若u∈H,则v∈H.
证明:记G[H]的核值为p,若u∈H,则p≤core(u).不妨假设包含{v}的k-MSC为G[H'],若HH',那么考查由HH'生成的导出子图G[HH']:
(1) G[HH']一定是连通的.这是由于G[H]和G[H']均是连通的并且二者通过(u,v)连接;
(2) 对于顶点w∈HH',w在G[HH']中一定至少有p个邻居.这是由于G[H]中顶点的度至少为p且G[H']中顶点的度至少为core(v)≥p,而G[HH']中顶点的度不会小于前两者.
因此,我们找到了一个G[H]的超图G[HH']并且G[HH']是p-SC,矛盾!故而H=H',即,顶点u和v一定出现在同一个k-MSC中. □
结论1. 在图G=(V,E)中,若u≡v,则对于图G中任意一个最大Steiner连通k核G[H],若u∈H,则v∈H.
证明:根据引理1,易证该结论. □
根据上述结论可知,属于相同等价类的顶点一定会出现在相同的k-MSC中.这说明本文中等价关系的定义是合理的.
定理1. 给定图G=(V,E),GC=(VC,EC,f)是由SC算法计算的压缩图,若HC是GC中的一个k-MSC,则H是G
中的一个k-MSC,其中,H={v|vu,u∈HC}.
证明:用反证法.若G[H]不是一个k-MSC,则图G中要么存在一个G[H]的超图G[H'],使得G[H']是k-SC;要么存在一个G[H],使得G[H]的核值比G[H]更大.
首先讨论第1种情况.由于G[H']是连通的,不妨假设w∈H'\H且w与H相邻.显然,w对应的等价类[w]CHC.根据结论1可以发现:(1) GC[HC{[w]C}]是连通的;(2) GC[HC{[w]C}]的核值不小于GC[HC].矛盾!故第一种情况是不存在的.
下面讨论第2种情况.若存在一个核值更大的G[H],则记${{{H}'}_{C}}$={u∈VC|vu,v∈H}.根据SC算法,若(u,v)∈E,则([u]C,[v]C)∈EC,故${{G}_{C}}[{{{H}'}_{C}}]$一定是连通的.因此,我们在压缩图GC中找到了一个核值更大的k-SC,这意味着GC中一定存在着一个核值更大的k-MSC.矛盾!故第2种情况也是不存在的.
综上所述,可证结论. □
定理2. 给定有向图G=(V,E),查询顶点集Q,GC=(VC,EC,f)是由SC算法计算的压缩图,QC是Q对应的等价类集,则在原始图G上包含Q的k-MSC与在压缩图GC上包含QC的k-MSC是相同的.
证明:根据定理1,在压缩图GC上包含QC的k-MSC一定是原始图G中包含{v|vu,u∈QC}的k-MSC.下面只需证明在原始图中,查询顶点集Q和{v|vu,u∈QC}具有着相同的k-MSC.
根据结论1,同一等价类中的顶点一定在同一个k-MSC中,故定理2得证. □
2.2 SC算法的分析SC算法采用了基于等价类的压缩思想,因此,如何有效地划分等价类是SC算法的关键.
首先需要计算图中所有顶点的核值,根据文献[11]中的算法,通过使用桶排序,所有顶点核值的计算可以在O(|E|)内完成.见算法1第1行.
其次,为了划分等价类,将依次为每一个顶点分配唯一的类别.根据定义5,u≡v当且仅当图中存在P(u,v),使得对于任意顶点w∈P(u,v),core(w)=core(u)=core(v).因此可以从任意的顶点u出发,采用广度优先搜索算法,不断地扩展与顶点u核值相同的顶点,直至无法扩展为止.将上述顶点集划分为同一等价类[u]C,同时标记为已访问.至此,顶点u所在的等价类划分完毕.对于图中剩余的等价类,只需要不断重复上述过程,直至图中所有顶点均被访问过为止,见算法1第3行~第11行.显然,基于BFS的等价类划分可以在O(|E|)的时间内完成.
最后,通过依次访问原始图G中的每一条边,可以确定压缩图的边集.显然,生成压缩图仍然可以在O(|E|)内完成.故,图压缩算法SC的时间复杂度为O(|E|).
算法1. SC.
Input: Graph G=(V,E);
Output: Compressed Graph GC=(VC,EC,f),Map List M.
① Kcore();
② VC=EC=;
③ For each u∈V do
④ If u is not visited then
⑤ BFS(core(u)); //仅扩展与u核值相同的顶点
⑥ For each v expanded by BFS(core(u)) do
⑦ M[v]=[u]C;
⑧ v is visited;
⑨ end for
⑩ VC=VC[u]C,f([u]C)=core(u);
⑪ M[u]=[u]C,u is visited;
⑫ end if
⑬ end for
⑭ For each vertex pair [u]C∈VC,[v]C∈VC do
//计算压缩图的边集
⑮ if (u,v)∈E then
⑯ EC=EC([u]C,[v]C);
⑰ end if
⑱ end for
⑲ return GC=(VC,EC),M ;
值得注意的是:图压缩算法SC在返回压缩图GC的同时还将返回一个映射表M,M记录了原始图中每一个顶点所对应的等价类.借助于M,对于给定查询(G,Q),可以在O(|Q|)时间内将之转换为(GC,QC),以用于进一步的查询处理.由于M的规模为O(|V|),故可将M存放于内存,且由于M的大小并不影响查询速度,故不将M计入压缩图.
另外,压缩图需要额外保存顶点的核值信息.这是由于压缩后顶点的邻居信息不再完整,即:如果不保存核值信息,那么将无法从压缩图得到正确的k-MSC结果.而在真实的图数据中,顶点的核值往往是比较小的,比如在Brightkite和Gowalla两个社交网络中,顶点的最大核值分别为52和51.而在道路交通网络中,顶点的核值更小,比如roadNet-CA网络中,顶点最大核值仅为3.这说明压缩图中用于保存顶点权值所占的空间是很小的,故在考查压缩比时,仍然以|EC|/|E|为准.
3 最大生成树压缩算法TC本文将在SC算法的基础上给出第2种图压缩算法TC,从而将压缩图GC进一步压缩.TC算法的大致思想为:将压缩图GC中的边进行适当选择,得到一棵树GT=(VT,ET,f),使得VT=VC;且对于查询(GC,QC),通过计算(GT,QC)可以得到相同的查询结果.
上述思想来自于对压缩图GC上查询过程的观察.在计算包含QC的k-MSC时,可以分为两个步骤:(1) 找到包含QC的一个连通区域C,记C的权值为C中顶点权值最小者,即f(C)=Min{f(u)|u∈C},那么查询所要找到的C是所有包含QC的连通区域中权值最大者;(2) 在保持权值不变和连通的前提下,将C扩展至极大,得到H,H即为包含QC的k-MSC.根据k-MSC的定义和结论1,上述查询结果显然是正确的.由于步骤(2)依然可以使用广度优先搜索算法实现,故问题的关键在于如何发现包含QC且权值最大的连通区域C.
计算C可以进一步地分解为不断地构建连接QC中顶点对的简单路径.记QC={u1,u2,…,up},那么计算C就可以看作依次构建p-1条简单路径:P(u1,u2),P(u1,u3),…,P(u1,up).记每条简单路径P的权值为P上顶点权值最小者,即f(P)=Min{f(u)|u∈P},那么查询所要找到的每一条P(u1,ui)都是连接顶点u1和ui的所有简单路径中权值最大者.
以图 1(b)中的压缩图GC为例,若查询顶点集为{8,12,15},则转换后可知QC={u3,u5}.那么查询过程分为以下两步:首先,找到包含{u3,u5}的权值最大的连通区域,该过程可以进一步转换为计算权值最大的P(u3,u5),易知,路径(u3,u4,u5)是符合条件的,因此C={u3,u4,u5}且f(C)=2;最后,在保持连通性和权值不变的前提下, 将C进一步扩展为{u2,u3,u4,u5},那么GC[{u2,u3,u4,u5}]就是最终的查询结果.
定义6. 给定图G=(V,E,W),W是边集E上的权值函数,G的子图G1是一棵生成树当且仅当G1是树且G1包含了G中全部顶点,若G1在所有生成树中具有最大的权值和,则G1为最大生成树.
下面证明GC=(VC,EC,f)的最大生成树GT=(VT,ET,f)满足本文的查询要求,即:对于查询(GC,QC),计算(GT,QC)可以得到相同的查询结果.这里需要强调的一点是:对于EC中每条边(u,v)的权值,取(u,v)两端的顶点中权值较小者.这是因为当路径P经过(u,v)时,f(P)一定不会超过u和v中权值较小者.
定理3. 给定图GC=(VC,EC,f),GT=(VT,ET,f)是GC的最大生成树,则对于顶点u∈VC,v∈VC,P(GT,u,v)是图GC中连接u和v的权值最大的简单路径.
证明:用反证法.假设P(GT,u,v)在图GC中不是权值最大的简单路径,那么一定存在一条权值更大的路径P'.下面通过例子来说明.以图 1(c)为例,不妨设P(GT,u,v)=(u2,u3,u6),P'=(u2,u4,u6).那么向GT中增加两条边(u2,u4)和(u4,u6),此时,GT中至少产生了两个环.首先找到路径P(GT,u,v)上权值最小的边(u3,u6)并将之删除;然后,GT中还存在着一个环.继续删除剩余环中权值最小的边(u2,u3),得到一棵新的生成树${{{G}'}_{T}}.$
在上述过程中,可以将插入边和删除边的操作配对,即:首先插入边(u4,u6),随后产生环(u3,u4,u6),再删除边(u3,u6)破坏环得到新的生成树;然后插入边(u2,u4),产生环(u2,u3,u4),再删除边(u2,u3)得到${{{G}'}_{T}}.$
因为P'的权值大于P(GT,u,v),故首次产生环并破坏环的操作一定使生成树的权值和增大.又因为每次产生环并破坏环的操作一定不会令生成树的权值和减小,故${{{G}'}_{T}}.$的权值和一定大于GT,所以GT不是最大生成树.矛盾!故结论成立. □
定理4. 给定图GC=(VC,EC,f),GT=(VT,ET,f)是GC的最大生成树,则(GC,QC)与(GT,QC)的查询结果相同.
证明:用构造法证明.根据定理3,对于u∈QC,v∈QC,P(GT,u,v)一定是图GC中连接u和v的权值最大的简单路径,那么对于QC={u1,u2,…,up},通过依次构建p-1条简单路径:P(GT,u1,u2),P(GT,u1,u3),…,P(GT,u1,up),并据此形成的连通区域C={v|v∈P(GT,u1,ui),0<i<p}一定是所有包含QC的连通区域中权值最大的.然后,在保持连通性和权值不变的前提下,将C扩展至极大至H,显然,GC[H]即为包含QC的k-MSC.
故结论成立. □
下面分析图压缩算法TC的时间复杂度.根据文献[22],在使用斐波那契堆进行排序时,最大生成树算法可以在O(|E|+|V|log|V|)内完成.注意到压缩图GC边上的权值均为顶点的核值,即整数,故本文将采用桶排序算法,从而将TC算法的时间复杂度降至O(|VC|+|EC|).
下面介绍本文所使用桶的数据结构.桶以链表的形式存储,每个桶对应着一个权值,即顶点核值.为了提高插入删除操作的效率,还需要两个额外的数据结构:首先,为了提高插入效率,为每一个桶记录一个尾部指针,当桶中有新的元素加入时,只需在尾部增加即可,故插入的时间复杂度为O(1);其次,为了提高删除效率,为每一个桶内的元素记录其父亲元素的指针,当该元素要从桶中删除时,只需将令父亲指向其儿子即可,故删除的时间复杂度为O(1).由于TC算法执行过程中至多向桶中插入/删除|EC|次,故可将TC算法的时间复杂度降至O(|VC|+|EC|).算法2中给出了TC算法的具体执行过程.
算法2. TC.
Input: Compressed Graph GC=(VC,EC,f);
Output: Compressed Tree GT=(VT,ET,f).
① For each u∈V do
② For each v∈N(u) do
③ insert (u,v) into Bins;
④ end for
⑤ u is visited;
⑥ while Bins is not empty do
⑦ extract (x,y) with maximum value,;
//此处认为x已被访问过,y未被访问过
⑧ insert (x,y) into ET;
⑨ For each v∈N(y) do
⑩ if v is not visited then
⑪ insert (y,v) into Bins;
⑫ else
⑬ delete (y,v) from Bins;
⑭ end if
⑮ end for
⑯ y is visited;
⑰ end while
⑱ end for
⑲ Return GT=(VC,ET,f);
最后介绍关于在压缩图GT=(VT,ET,f)上的查询算法.因为压缩图GT是一棵树,故可以有效地利用树的结构提高查询效率.在查询前,可以首先作以下预处理:
(1) 选取度值最大的顶点作为根节点,当出现度值相等的情况时,选取核值大的顶点作为根节点.这样做的好处是可以让树尽可能均衡,因为度值大意味着树的深度较小,而核值大意味着该顶点可出现在更多的k-SC中;
(2) 计算每个顶点到根的距离,即顶点的深度.显然,预处理的时间复杂度为O(|V|+|E|),而上述预处理的结果均不会存储于压缩图中.
压缩图GT上的查询算法QueryGT见算法3.首先,依次计算QC={u1,u2,…,up}中相邻顶点ui和ui+1的最小公共祖先[23]:LCA(ui,ui+1),其中,LCA(ui,ui+1)是指在一棵有根的树中,ui和ui+1的公共祖先中距离根节点最远的.在计算出LCA(u1,u2)后,记u2=LCA(u1,u2)并继续计算LCA(u2,u3),然后记u3=LCA(u2,u3)并继续计算LCA(u3,u4),以此类推.显然,最终得到的LCA一定是顶点集QC中所有顶点的最小公共祖先,记作LCA(QC).而借助于预处理中顶点的深度信息,上述过程所访问的所有顶点形成了一棵以LCA(QC)为根的子树,且该子树一定是包含QC的k-MSC的子图.事实上,该子树正是前文所提到的包含QC的权值最大的连通区域C.
然后,在保持连通性和权值不变的前提下,对上述子树进行BFS扩展,可得到极大子图GC[H],即为最终查询结果.显然,QueryGT算法仅需访问查询结果集中的顶点,故其时间复杂度为O(|RQ|).
算法3. QueryGT.
Input: Compressed Graph GT=(VT,ET,f),Query Set Q,Map List M;
Output: k-MSC H which contains Q.
① compute QC based on Q and M,min=|VT|-1,H=; ;
② for 0<i<|QC| do
③ compute LCA(ui,ui+1);
④ if v is visited during LCA computation then
⑤ v is visited,min=Min{f(v),min},H=H{v};
⑥ end if
⑦ ui+1=LCA(ui,ui+1);
⑧ end for
⑨ push(Queue,LCA(QC)); //扩展计算极大子图
⑩ while Queue is not empty do
⑪ u=pop(Queue);
⑫ for each v∈N(u) do
⑬ If v is not visited and f(v)≥min then
⑭ push(Queue,v),v is visited,H=H{v};
⑮ end if
⑯ end for
⑰ end while
⑱ Return H ;
4 实验结果在实验部分,本文在真实数据集上对两种图压缩算法SC和TC的有效性和查询效率进行了考查.在考查压缩比时,使用SMCC索引作为对比;在考查查询效率时,使用了直接在原始图上查询的直观算法Base的查询算法作为对比.为验证SC和TC算法的扩展性,本文还在虚拟数据集上检验了两种算法的压缩比和查询效率.
下面首先介绍实验考查的几种测度,包括压缩算法压缩比和查询处理时间;随后介绍使用的实验数据、实验环境和对比实验;最后给出实验的对比及分析.
在考查算法的压缩比时,分别用CRSC和CRTC表示压缩算法SC和TC算法的压缩比,其中,CRSC=|EC|/|E|,CRTC=|ET|/|E|.可知:当压缩比越小时,压缩图的规模也越小,说明压缩算法更加有效.在考查查询处理时间时,对比了基于压缩树的查询处理算法QueryGT的时间开销与在原始图上直接进行查询的Base算法的时间开销.为公平起见,Base算法并不计算原始图中顶点的核值,即,认为顶点核值也是Base算法的输入.
实验中使用的真实数据集来源于斯坦福大学的共享数据集(http://snap.stanford.edu/data/#twitter).本文使用的数据规模在404K~23.9M之间,包括了以下网络:(1) Email-Enron,美国安然公司的邮件网络,其中,顶点表示邮箱,边表示某个邮箱向另一邮箱发送过邮件;(2) ca-AstroPh,天体物理学期刊Arxiv中的作者合作网络,其中,顶点表示作者,边表示两位作者合作过;(3) Brightkite和Gowalla,在线社交网络,其中,顶点表示用户,边表示朋友关系;(4) roadNet-TX和roadNet-CA,美国德克萨斯州和加利福尼亚州的道路交通网络,其 中,顶点表示道路交汇点,边表示道路;(5) as-Skitter,互联网拓扑图,其中,顶点表示网页,边表示超链接.表 1中给出了本文所使用真实数据集的特性,其中,平均度数为|E|/|V|,反映了图的稠密程度;最大核值为图中核值最大的顶点,反映了图中最稠密社团的稠密度.实验所使用虚拟图是基于偏好模型生成的[24],即:图中顶点更容易和度数大的顶点共同组成一条边,而不容易和度数小的顶点组成边.为了突出少数顶点的度数,图中将初始化一个规模为平均度数的团,为使虚拟图能适用于实验,将人为去掉图中的自环和多重边.
| Table 1 Properties for real datasets 表 1 实验中使用真实数据集的基本特性 |
上述实验使用C++实现,在双核3.40GHz Intel Core(PM) D CPU、32.0GB内存、Window7系统的台式机上运行.
表 2中给出了SC,TC算法和SMCC索引在真实数据集上的压缩比.实验结果表明:(1) 图压缩算法的压缩效果非常可观,且对于稠密图将取得更好的压缩比;(2) TC算法可以在SC算法的基础上进一步有效地压缩原始图.首先可以发现:所提出图压缩算法的平均压缩比为12%,而对于平均度数大于10的Email-Enron,ca-AstroPh和as-Skitter,压缩比则接近10%.其中,对于平均度数为21.1的作者合作网络ca-AstroPh,压缩图规模仅为原始图的3.9%.除道路交通网络外,最稀疏的Brightkite的压缩效果最差,但是也达到了17.8%.这是由于稠密图中往往会出现多个稠密区域,而这些稠密区域就很可能会被压缩算法归为同一个等价类,故本文的压缩算法对于稠密图更有效.其次,除去道路网络图,可以发现,TC算法可以将SC算法得到的压缩图GC进一步压缩3~5倍.比如:对于as-skitter,SC算法可以将原始图压缩至42.1%,而TC算法则可进一步将其压缩至10.5%;而对于ca-AstroPh,尽管SC算法的压缩比已经比较客观,为19.4%,但是TC算法仍然能进一步将压缩效果提升至3.9%.这说 明两种算法都是必要的.
| Table 2 Compressed graph size and compression time of SC,TC and index size of SMCC on real datasets 表 2 真实图数据上SC,TC的压缩图大小、压缩时间与的SMCC索引大小 |
在道路交通网络中,尽管顶点的平均度数很小(往往不超过3),但是由于道路交通网络中的稠密区域大部分都很稀疏(这一点可以在表 1中发现,roadNet-TX和roadNet-CA的最大核值均仅为3),所以道路交通网络更加容易被基于等价类划分的SC算法压缩.可以发现,TC算法在上述两个数据集上无法将SC算法得到的压缩图GC进一步压缩.这说明仅使用SC算法,就能够将道路交通网络图充分压缩.
与SMCC索引相比,本文所使用的图压缩算法具有更好的压缩性能.SMCC索引的平均压缩比为33%,这几乎是所提出算法的3倍.可以发现:在Brightkite,Gowalla和as-skitter上,SMCC索引的规模更小,仅为压缩图的1.5倍;而在roadNet-TX和roadNet-CA上,SMCC索引的规模都超过了原始图的70%,这意味着SMCC索引几乎无法将原始图压缩.上述情况的出现是由于道路交通网络是十分稀疏且连通的,因此几乎可以看作一棵树,而SMCC索引 的思想就是将原始图表示成树,故SMCC索引几乎不能缩减道路交通网络的规模.
表 2还给出了SC,TC算法的压缩时间,实验结果表明:两种压缩算法的压缩时间都很快速.对于规模最大的road-CA和as-skitter,压缩算法分别可在1s和8s内完成.
图 2给出了Base算法与基于压缩图的QueryGT算法在真实图上的查询时间对比,所使用的图包括Gowalla,roadNetTX和as-skitter.这是由于邮件网络Emai-Enrom、作者合作网络ca-AstroPh和在线社交网络Brightkite、Gowalla均具有相似的社交网络的特性,road-TX和road-CA均为道路网络,而as-skitter则代表着网络图,故本文仅以3类图数据中规模较大的Gowalla,road-TX和as-skitter为例考查基于压缩图的查询效率.查询顶点集是1 000组随机生成的、大小从5增加至10的顶点集,查询时间是1 000组查询时间的总和.实验结果表明:(1) QueryGT的查询效率比Base提高了一至两个数量级;(2) 两种算法的查询时间均随着给定查询顶点集大小|Q|的增大而略有增加.首先可以发现:对于Gowalla和roadNet-TX,QueryGT的查询速度是Base的50~60倍;而对于as-skitter,QueryGT的查询效率则是Base的200倍左右.这是由于图压缩算法不仅将原始图进行了有效地压缩,且保证了QueryGT在压缩图上查询时仅仅需要访问查询结果集中的顶点,因此查询效率得到极大的提升.其次,当查询顶点集大小|Q|从5增加至10时,两种算法的查询时间均有微小的增加.这是因为随着查询顶点集的增大,查询结果将有可能变成核值更小、覆盖顶点更多的连通区域,这将使查询结果集变得更大,而两种算法的运行时间均与查询结果集大小相关,故查询时间会随之增加.

|
(a) Gowalla数据集 (b) roadNet-TX数据集 (c) as-skitter数据集 Fig. 2 Query time of Base vs. QueryGT on real datasets 图 2 真实图数据上查询算法Base和QueryGT的对比 |
图 3(a)~图 3(d)给出了SC和TC算法在虚拟图上的压缩比,为了验证算法的扩展性,分别在顶点数为1M~ 10M时,将虚拟图的边数从9.8M增加至274M.

|
Fig. 3 Compression ratio and compression time of SC,TC on synthetic datasets 图 3 虚拟图数据上SC,TC算法的压缩比与压缩时间 |
实验结果表明:图压缩算法在虚拟图上仍然就有很好的压缩效果;且随着平均度数的增加,压缩图的规模更小.即,算法更适用于稠密图.首先可以发现:压缩算法在顶点数为1M~10M的虚拟图上都取得了平均低于12%的压缩比,这说明压缩算法可以将虚拟图有效地压缩;当虚拟图的平均度数为20左右时(即边数为19.9M,42.3M,99.3M,224M时),两张虚拟图压缩后的规模均在原始图规模的10%左右.其次,当顶点数固定、边数增加时,算法的压缩比从19.8%降至6.7%,且保持了单调下降的趋势.这说明压缩算法更加适用于稠密图.值得注意的一点是:在虚拟图上,SC和TC算法的压缩效果极为接近,这是由于在偏好模型下,少数度数较大的顶点将构成一个等价类,而剩余小度数的顶点经过SC算法的压缩将非常稀疏,即接近于树,因此TC算法无法将上述压缩图进一步大幅度压缩.这说明SC算法在本文所使用的虚拟图模型下更加适用.图 3(e)和图 3(f)给出了SC,TC算法在虚拟图上的压缩时间,实验结果表明,两种算法的压缩时间仍然都很快速.对于顶点数为5M和10M、边数为61M~274M的虚拟图,压缩算法可在40s内完成.
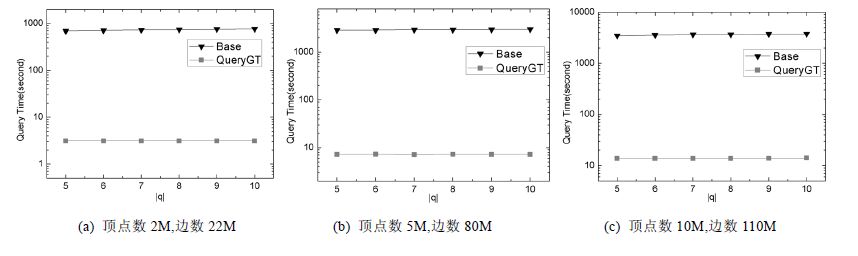
图 4给出了Base算法与基于压缩图的QueryGT算法在虚拟图上的查询时间对比,其中,查询顶点集是1 000组随机生成的、大小从5增加至10的顶点集,查询时间是1 000组查询时间的总和.实验结果表明:(1) QueryGT的查询效率比Base提高了两个数量级;(2) 两种算法的查询时间均随着给定查询顶点集大小|Q|的增大而略有增加.首先可以发现:当顶点数分别为2M,5M和10M、边数分别为22M,80M和110M时,QueryGT均比Base快两个数量级;且对于更加稠密的前者,查询效率提升的更加明显.这是由于图压缩算法对于稠密图会取得更好的压缩效果,从而令查询效率得到更大提升.其次,当查询顶点集大小|Q|从5增加至10时,两种算法的查询时间均有微小的增加.这是因为随着查询顶点集的增大,查询结果将有可能变成核值更小、覆盖顶点更多的连通区域,故查询时间会随之增加.
|
(a) 顶点数2M,边数22M (b) 顶点数5M,边数80M (c) 顶点数10M,边数110M Fig. 4 Query time of Base vs. QueryGT on synthetic datasets 图 4 虚拟图数据上查询算法Base和QueryGT的对比 |
综上所述,本文所提出的图压缩算法无论在真实还是虚拟数据集上都能取得非常可观的压缩效果,且当原始图变得稠密时,算法的压缩效果更加显著.而基于压缩图的查询性能也得到了巨大的提升.
5 结束语本文研究了基于图压缩技术的k-MSC查询处理算法,提出了图压缩算法SC及在查询转换算法,证明了基于图压缩算法SC的查询的正确性.考虑到k-MSC查询仅需要找到符合要求的连通区域,本文提出了图压缩算法TC将SC算法得到的压缩图进一步压缩为树.本文证明了基于压缩树的查询的正确性,并给出基于压缩树的无需解压缩的查询算法.通过真实和虚拟数据上的实验结果表明:所提出图压缩算法的压缩比平均可达到12%;而对于稠密图,算法将取得更好的接近10%的压缩比.基于压缩算法的查询效率也得到了很好的提升,与直接在原始图上查询的Base算法相比,查询效率提高了1~2个数量级.在今后的工作中,我们将进一步探讨针对本文压缩方法的更新技术.
致谢 在此,我们向曾经对本文提出宝贵审稿建议的审稿专家以及哈尔滨工业大学计算机科学与技术学院的李建中教授表示衷心的感谢.| [1] | Smith C.By the numbers:98 amazing facebook statistics.DMR,2014. |
| [2] | Agrawal R,Rajagopalan S,Srikant R,Xu Y.Mining newsgroups using networks arising from social behavior.In:Proc.of the WWW 2003.2003. |
| [3] | Lappas T,Liu K,Terzi E.Finding a team of experts in social networks.In:Proc.of the KDD 2009.2009. |
| [4] | Yan X,Zhou XJ,Han J.Mining closed relational graphs with connectivity constraints.In:Proc.of the KDD 2005.2005. |
| [5] | Asthana S, King OD, Gibbons FD, Roth FP. Predicting protein complexmembership using probabilistic network reliability. Genome Research, 2004, 14 (6) :1170–1175. [doi:10.1101/gr.2203804] |
| [6] | Hanneman RA,Riddle M.Introduction to Social Network Methods.University of California,Riverside,2005. |
| [7] | Seidman SB. Network structure and minimum degre. Social Networks, 1983, 5 :269–287. [doi:10.1016/0378-8733(83)90028-X] |
| [8] | Bollobas B. The evolution of sparse graphs,in graph theory and combinatorics. .In:Proc.of the Cambridge Combinatorial Conf.in Honor of Paul Erdos.Academic Press, 1984 :35–37. http://citeseerx.ist.psu.edu/showciting?cid=499610 |
| [9] | Kortsarz G, Peleg D. Generating sparse 2-spanners. Journal of Algorithms, 1994, 17 (2) :222–236. [doi:10.1006/jagm.1994.1032] |
| [10] | Andersen R, Chellapilla K. Finding dense subgraphs with size bounds. In:Proc.of the WAW, 2009 :25–37. http://cn.bing.com/academic/profile?id=1888358353&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | Batagelj V, Zaversnik M. An o (m) algorithm for cores decomposition of networks. Computer Science, 2003, 1 (6) :34–37. http://cn.bing.com/academic/profile?id=1676999057&encoded=0&v=paper_preview&mkt=zh-cn |
| [12] | Boldi P, Vigna S. The webgraph framework i:Compression techniques. In:Proc.of the 13th Int'l Conf.on World Wide Web.ACM Press, 2004 :595–602. http://cn.bing.com/academic/profile?id=1994727615&encoded=0&v=paper_preview&mkt=zh-cn |
| [13] | Chierichetti F, Kumar R, Lattanzi S, Mitzenmacher M, Panconesi A, Raghavan P. On compressing social networks. .In:Proc.of the 15th ACM SIGKDD Int'l Conf.on Knowledge Discovery and Data Mining.ACM Press, 2009 :219–228. http://cn.bing.com/academic/profile?id=2029852131&encoded=0&v=paper_preview&mkt=zh-cn |
| [14] | Maserrat H, Pei J. Neighbor query friendly compression of social networks. In:Proc.of the 16th ACM SIGKDD Int'l Conf.on Knowledge Discovery and Data Mining.ACM Pre, 2010 :533–542. http://cn.bing.com/academic/profile?id=2165971212&encoded=0&v=paper_preview&mkt=zh-cn |
| [15] | Fan W, Li J, Wang X, Wu Y. Query preserving graph compression. In:Proc.of the 2012 ACM SIGMOD Int'l Conf.on Management of Data.ACM Press, 2012 :157–168. http://cn.bing.com/academic/profile?id=2100132188&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | Buneman P, Grohe M, Koch C. Path queries on compressed XML. In:Proc.of the 29th Int'l Conf.on Very Large Data Bases-Vol.29.In:Proc.of the VLDB Endowment, 2003 :141–152. http://cn.bing.com/academic/profile?id=2165128972&encoded=0&v=paper_preview&mkt=zh-cn |
| [17] | Navlakha S, Rastogi R, Shrivastava N. Graph summarization with bounded error. In:Proc.of the 2008 ACM SIGMOD Int'l Conf.on Management of Data.ACM Press,, 2008 :419–432. http://cn.bing.com/academic/profile?id=2108781142&encoded=0&v=paper_preview&mkt=zh-cn |
| [18] | Newman ME, Girvan M. Finding and evaluating community structure in networks. Physical Review E, 2004, 69 (2) :026113. [doi:10.1103/PhysRevE.69.026113] |
| [19] | Huang X,Cheng H,Qin L,Tian W,Yu JX.Querying k-truss community in large and dynamic graphs.In:Proc.of the SIGMOD 2014.2014. |
| [20] | Cui W,Xiao Y,Wang H,Lu Y,Wang W.Online search of overlapping communities.In:Proc.of the SIGMOD 2013.2013. |
| [21] | Chang L, Lin X, Qin L, Yu JX, Zhang W. Index-Based optimal algorithms for computing steiner components with maximum connectivity. In:Proc.of the 2015 ACM SIGMOD Int'l Conf.on Management of Data.ACM Press, 2015 :459–474. http://cn.bing.com/academic/profile?id=1980162113&encoded=0&v=paper_preview&mkt=zh-cn |
| [22] | Gibbons A.Algorithmic Graph Theory.Cambridge University Press,1985. |
| [23] | Aho AV,Hopcroft JE,Ullman JD.On finding lowest common ancestors in trees.In:Proc.of the STOC'73.1973. |
| [24] | Bollobás B, Riordan O. The diameter of a scale-free random graph. Combinatorica, 2004, 24 (1) :5–34. [doi:10.1007/s00493-004-0002-2] |
 2016, Vol. 27
2016, Vol. 27


