2. 吉林大学 计算机科学与技术学院, 吉林 长春 130012 ;
3. 符号计算与知识工程教育部重点实验室 吉林 大学, 吉林 长春 130012
2. College of Computer Science and Technology, Jilin University, Changchun 130012, China ;
3. Key Laboratory of Symbolic Computation and Knowledge Engineer, Ministry of Education Jilin University;, Changchun 130012, China
随机块模型(stochastic blockmodel,简称SBM)是一类重要统计网络分析模型,因其可以有效处理不具有先验知识的网络,对其研究成为机器学习、社会网络分析和网络数据挖掘等领域的热点.SBM[1]模型中,块内节点具有连接模式上的同构性[1],分属同一个块的节点与网络其他节点的连接方式相似.另一方面,分属不同块的节点在连接方式上具有异构性.块连接矩阵可以灵活地描述网络节点连接模式的同构和异构特性.基于这一能力,SBM作为网络生成模型可产生具有不同拓扑结构的人工网络,如社区、多分和中枢等;作为预测模型,利用学习得到的参数值可对不具有先验结构知识的网络进行结构分析,如社区发现和链接预测.
因此,自1981年美国统计学家Fienberg和Wasserman提出SBM概念以来,引起了不同领域学者对其的广泛研究,并已提出了不同的改进版本以适应不同领域的需求,如刻画多角色的SBM[2]、刻画重叠社区结构的SBM[3]、发现探索式结构的SBM[4]、刻画无标度度分布的SBM[5]、发现动态社区结构的SBM[6]和刻画多尺度的SBM[7]等.SBM虽然在结构分析方面表现出其特有的优越性,但SBM学习算法的高复杂性使其仅能应用到小规模网络中.现有的SBM学习算法在给定块数K时,即学习算法不需要模型选择,其时间复杂度至少为O(K2n2),n为网络节点数;而当未给定块数K时,即学习算法需要模型选择,其时间复杂度至少为O(n5).更直观地讲,在通常的个人计算机配置下:已知块数K,现有方法仅能够有效处理几千节点规模的网络;未知块数K,现有方法实际能处理的网络规模只有几百节点.过高的时间复杂性,将SBM的应用限制在规模很小的网络中.如何设计出具有模型选择能力的快速随机块模型学习方法,是目前SBM研究面临的一个主要挑战.
针对以上问题,本文提出具有更好泛化能力的精细随机块模型RSBM(refined-SBM).基于该模型与最小消息长度推导出新的成本函数,利用期望最大化参数估计方法实现一种具有模型选择能力的随机块模型快速学习算法RFLA(RSBM fast learning algorithm).提出的学习算法采用边估计参数边评价模型的并行学习策略,只对“当前认为较好的”模型进行参数估计,以此方式显著降低学习的时间复杂性,实现可处理的网络规模从几百节点提高到几万节点以上.
1 相关工作SBM的学习可为两部分:参数估计与模型选择.参数估计即学习模型的参数W与P,模型选择即学习模型的块数K.不同的模型对应着不同数量的参数,参数越多,模型越复杂.SBM的参数数量由块数K决定,一旦确定了K值,即确定了相应模型的复杂度.例如:对于有向网络而言,参数总数目等于W包含的参数数目K与P的参数数目K2之和,共K2+K个.模型选择就是寻找能平衡模型精度与复杂度的最佳模型,因此对SBM而言,模型选择是指从数据中自动学习出合适的K值.给定K时,SBM学习算法的复杂度由模型空间及采取的参数估计算法确定,当未给定K时,学习算法的复杂度则由模型空间,模型选择策略和参数估计算法共同决定.
目前,SBM的参数估计算法主要有以下几类.
(1) 基于Gibbs采样的MCMC方法.早期的SBM[8]和动态SBM[6]采用此类方法估计参数.MCMC方法是一个迭代模拟方法,需要反复对每个未知的变量在条件依赖于其他变量的情况下进行抽样以得到参数的后验分布,收敛速度慢,计算复杂性很高,仅适用于小规模网络;
(2) EM算法.目前,该算法是SBM最常采用的参数估计算法[4],它利用吉布森不等式寻找观察数据似然的低边界.由于EM将指示变量Z作为隐含变量,算法在估计模型参数的同时,相应地确定了块结构,因此成为随机块模型学习的主要方法[4, 9].EM算法通过不断地迭代去寻找似然的低边界,每次迭代过程需利用全部数据同时更新参数与隐含变量的后验分布,导致计算成本高昂;
(3) 变分EM算法.近几年被广泛应用于SBM学习中,特别是具有复杂似然函数的各种扩展SBM,如多角色SBM[2]和重叠SBM[3].变分EM算法利用近似分布代替EM算法对参数的点估计,可获取比EM算法相对更好的精度和稳定性;
(4) 信念传播算法.该算法可准确计算隐含变量后验分布,2006年首次应用于SBM[10]的参数估计中.但该算法具有较大局限性,对含有回路的网络无法保证算法的收敛,仅适用于非常稀疏的网络.
对没有任何先验结构知识的网络进行分析时,我们通常无法预知真实的K值,因此要求SBM学习算法除了可以进行参数估计外,还需要具有模型选择能力.目前,应用于SBM的模型选择方法主要分为3类.
(1) 交叉验证法
该方法是可以与多种SBM学习算法相结合的模型选择方法,其每次从数据集中获得两个不同子集,分别用于建立模型和评估模型,虽然实现简单但计算开销巨大.2008年,Airoldi等人为验证多角色SBM模型,采用了交叉验证法进行模型选择[4].
(2) 基于贝叶斯的模型选择方法
该类方法计算模型证据(evidence),选择具有最大证据值的模型作为最优模型.由于证据计算非常困难,通常进行近似计算.根据不同的近似方法,基于贝叶斯的模型选择方法可分为3类.
(a) 基于拉普拉斯近似的BIC(Bayesian information criterion).该标准倾向于选择具有复杂度相对简单的模型.2008年,Airoldi等人提出的多角色SBM学习方法[2]利用该标准进行模型选择;
(b) ICL(integrated complete-data likelihood).该标准是针对混合模型观察数据似然难以计算的问题而提出,利用完整数据似然近似证据.相比于BIC标准,在混合模型中,ICL具有更好的效果,但当网络规模较小时该标准常误分块的数目.2008年,Daudin等人[11]提出的SICL算法,利用该标准进行模型选择;
(c) 基于变分的证据近似.该类方法利用变分技术近似参数的后验分布,计算证据低边界进行模型选择. 2008年,Hofman等人基于约束(constrained)SBM提出的VBMOD学习方法[12]采用此类方法进行模型选择.2012年,Latouche等人[13]提出的ILvb标准也属于此类方法,他们的实验表明,ILvb是目前准确度最高的模型选择方法.
(3) 基于信息编码理论的最小描述长度(minimum description length,简称MDL)准则
其原理及特点都与BIC相似,适合于小规模网络分析.2012年,杨博等人提出的GSMDL学习方法采用MDL准则进行模型选择[7].
上述模型选择方法本质上都属于串行学习方法,即:从候选模型空间中依次选择一个模型进行学习,然后评价学习的模型好坏,直至对所有候选模型完成学习与评价,最后从中选择最好的模型.设包含真实块数K的候选模型集为[Kmin,Kmax],则这种学习策略可表示如下:
| $\bar{K}=\arg \underset{K}{\mathop{\min }}\,\{C(\bar{\theta }(K),K),K={{K}_{\min }},...,{{K}_{\max }}\}$ | (1) |
其中,$\bar{K}$表示最优的模型,$C(\bar{\theta }(K),K)$表示模型选择准则的成本函数,$\bar{\theta }(K)$是估计的参数.通常,成本函数有如
下形式:
| $C(\bar{\theta }(K),K)=-\log p(D|\bar{\theta }(K))+P(K)$ | (2) |
其中,$\log p(D|\bar{\theta }(K))$表示数据的最大对数似然,P(K)是用于惩罚较高K值的递增惩罚函数.
串行学习方法需要针对模型空间的每一个模型进行参数估计,计算成本函数,使得有模型选择能力的SBM学习算法的复杂度远高于无模型选择能力的学习算法.特别是,当面对无任何先验知识的网络进行结构分析时,理论上应在Kmin=1~Kmax=n的候选模型空间进行搜索,致使具有模型选择能力的学习算法的时间复杂度至少为O(n5),例如经典的SICL算法[11]、最新提出的SILvb算法[12]及GSMDL算法[7]等.
相比无模型选择能力的SBM学习算法,有模型选择能力的SBM学习算法可在无任何先验知识的情况下准确获悉网络结构的特性,真正充分发挥SBM模型在网络结构分析方面的优势.然而,有模型选择能力的SBM学习算法过高的复杂度限制了模型应用,使其仅能处理几百节点的小型网络.为此,2008年,Hofman等人提出了VBMOD方法,通过将描述块连接的参数由K2减为2个,使算法时间复杂度降至O(n4).VBMOD算法是目前时间复杂度最低的具有模型选择能力的SBM学习算法,但参数的过度简化降低了SBM模型刻画网络结构的灵活性,使其仅能分析单纯的社区或多分结构,而不能分析混合结构.如何在保持模型灵活性及学习准确度的前提下降低学习的时间复杂度,使其可以处理相对较大规模的未知网络,已成为SBM研究面临的一个开放性问题.
2 本文的研究动机与贡献在综述现有SBM学习方法的基础上,我们认为,提出低复杂度并具有模型选择能力的SBM学习方法,需要解决如下两个问题.
(1) 降低参数估计的时间复杂性.由于待估计的模型参数中包含隐含变量,现有方法大多采用类似EM的迭代方法估计参数,这类方法的计算量随网络规模n和块数K的增加而急速增加;
(2) 降低模型选择的时间复杂性.目前,具有模型选择能力的SBM学习方法都采用模型选择和参数估计的串行策略,即使不好的模型同样需要进行学习,导致大量的计算成本耗费在学习不好的模型中.
最小信息长度MML(minimum message length)与MDL相似,都基于信息编码理论,认为最优模型生成的数据有最短的编码.但不同于MDL,MML考虑了参数的先验影响,相比于MDL具有更高的准确性[14].由于不同的模型通常具有不同的先验分布,这启发我们设计一个可以实现模型选择与参数估计的并行学习策略,进而提出一个具有模型选择能力的SBM模型快速学习方法.本文的主要贡献为:
(1) 提出精细随机块模型.该模型采用块到节点的连接关系描述网络结构,相对于SBM模型仅利用粗糙的块连接关系描述网络结构,提出的模型可以捕捉到更细致的网络结构信息,具有更好的泛化能力;
(2) 提出具有较低复杂度的SBM快速学习算法.提出的学习算法利用并行策略进行模型选择与参数估计,有效降低了学习的时间复杂性.相比现有采用的串行学习策略的SBM算法,学习过程中,只对好的模型进行参数估计,实现边估计参数边选择模型的并行计算,在参数估计的迭代过程中同时完成模型选择.
本文第3节介绍提出的模型与学习方法.第4节利用人工网络与真实网络验证所提的模型与算法.第5节给出算法应用实例.第6节总结全文.
3 模型与方法 3.1 精细随机块模型
标准SBM只利用参数Π(块连接矩阵)粗略的描述连接的同构和异构特性,难以表达出更细致的结构信息,导致模型的泛化能力低.针对该问题,我们将参数Π分解为两个参数Θ和
给定有向网络N=(V,E),其中,V(N)表示节点集,E(N)表示边集.Anxn是网络N的邻接矩阵,Aij表示节点i到节点j之间是否存在一条边:Aij=1表示有边,Aij=0表示没有边.如果网络N是无向的,则Aij=Aji.RSBM定义为X=(K,Z,Ω,Θ,
| Table 1 Symbols of RSBM and their descriptions 表 1 RSBM有关符号与参数描述 |
如果N是无向网络,则Θ=
| ${{\Pi }_{1}}=\Theta Z{{D}^{-1}},{{\Pi }_{2}}=\Delta Z{{D}^{-1}}$ | (3) |
其中,D=diag(nΩ).对无向网络,有Π1=Π2=Π.因此,SBM可看作RSBM的特例.相比SBM,推广后的RSBM通过Θ和
RSBM也可作为网络生成模型,一个网络N可按如下过程生成:
1) 每个节点按概率Ω分配到不同的块;
2) 块内每个节点按照连接概率Θ生成链接到其他节点的有向边;
3) 每个节点按照连接概率
RSBM生成的网络N的对数似然函数可表示为
| $\log p(N|\Omega ,\Theta ,\Delta )=\sum\limits_{i=1}^{n}{\log \sum\limits_{k=1}^{K}{\left( \prod\nolimits_{j=1}^{n}{f({{\theta }_{kj}},{{A}_{ij}})f({{\delta }_{kj}},{{A}_{ji}})} \right){{\omega }_{k}}}}$ | (4) |
其中,f(x,y)=xy(1-x)1-y.完整数据的对数似然可表示为
| $\log p(N,Z|\Omega \text{,}\Theta \text{,}\Delta )=\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{K}{{{z}_{ik}}\left( \sum\limits_{j=1}^{n}{\log (f({{\theta }_{kj}},{{A}_{ij}})f({{\delta }_{kj}},{{A}_{ji}}))}+\log {{\omega }_{k}} \right)}}$ | (5) |
Newman等人[4]提出的模型也可描述块到节点的连接关系,但该模型要求每个块内的节点至少存在一个出度不为0的节点,否则无法满足约束条件$\sum\nolimits_{i=1}^{n}{{{\theta }_{ri}}}=1$,从而无法正确发现某些结构[15].为此,Ramasco等人[15]通过分解参数q为3个参数$\vec{\theta },\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{\theta }$和$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\theta }$,较好地解决了该问题.本文提出的RSBM与上述模型区别在于两点.
· RSBM假设块内节点与每个节点之间的链接服从伯努利分布(即,考虑了无链接的情况),从而去掉了约束条件$\sum\nolimits_{i=1}^{n}{{{\theta }_{ri}}}=1$或$\sum\nolimits_{i=1}^{n}{({{{\vec{\theta }}}_{ri}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{\theta }}}_{ri}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\theta }}}_{ri}})}=1$;而上述模型因未考虑无链接的情况,则必须施加该约束条件;
· 基于RSBM可将EM算法与MML进行整合,从而从实现对模型的快速学习;而基于上述模型则无法实现对模型的快速学习.
3.2 快速学习方法本文提出的RSBM快速学习算法简记为RFLA(RSBM fast learning algorithm),该方法从两方面降低学习算法的复杂度:一是采用收敛速度更快的CEMM(component-wise EM for mixture)算法[16]进行参数估计;二是基于RSBM与MML(minimum message length)[14]推导出新的成本函数,该成本函数与CEMM进行整结合实现参数与模型的快速学习.算法在每次迭代学习时仅更新一个块,并对该块对应的子模型进行评价.CEMM算法仅估计存在概率不为0的块对应的模型参数,而存在概率为0的块直接消亡,进而实现参数估计与模型选择的并行执行,有效降低学习算法的计算复杂度.下面从参数估计和模型选择两个方面具体描述RFLA算法.
3.2.1 参数估计算法因为指示变量Z的存在,难以直接利用最大似然法进行模型参数估计,因此通常采用EM算法解决此类问题.CEMM算法作为EM算法的一种改进算法,通过E步与M步连续生成参数的估计序列,直到算法收敛.但CEMM与标准EM的区别在于CEMM在M步对参数的估计,即:标准EM在M步一次同时更新所有块的参数,而CEMM在M步一次仅更新与一个块相关的参数.这个特性使其能够及时的将块的信息变化传递给下一块的参数估计所用,从而加快算法的收敛.
E步:给定观察到的网络N与模型参数ht-1,计算完整数据对数似然函数的条件期望,即公式(6)中的Q函数.其中,h表示模型参数(Ω,Θ,
| $Q(h,{{h}^{t-1}})=E[\log (N,Z)|N,{{h}^{t-1}}]=\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{K}{{{\gamma }_{ik}}\left( \sum\limits_{j=1}^{n}{(\log f({{\theta }_{kj}},{{A}_{ij}})+\ln f({{\delta }_{kj}},{{A}_{ji}}))}+\log {{\omega }_{k}} \right)}}$ | (6) |
其中,gik=E[zik],表示在模型ht-1下,块i属于块k的后验概率.
M步:最大化对数似然估计模型参数,通过求导Q函数,即公式(6)取极值,可计算相应的参数.但由于存在约束$\sum\nolimits_{k=1}^{K}{{{\omega }_{k}}}=1$,因此这是一个求解带约束的极值问题,需要借助拉普拉斯算子进行求解,即:对公式(7)求导取极
值,可得到参数h的解析表达式(8)~表达式(10):
| $J=Q(h|{{h}^{t-1}})+\beta (\sum\nolimits_{k=1}^{{{K}_{\max }}}{{{\omega }_{k}}}-1)$ | (7) |
| $\omega _{k}^{(t)}=\frac{\sum\nolimits_{i=1}^{n}{{{\gamma }_{ik}}}}{n}$ | (8) |
| $\theta _{kj}^{(t)}=\frac{\sum\nolimits_{i=1}^{n}{{{A}_{ij}}{{\gamma }_{ik}}}}{\sum\nolimits_{i=1}^{n}{{{\gamma }_{ik}}}}$ | (9) |
| $\delta _{kj}^{(t)}=\frac{\sum\nolimits_{i=1}^{n}{{{A}_{ji}}{{\gamma }_{ik}}}}{\sum\nolimits_{i=1}^{n}{{{\gamma }_{ik}}}}$ | (10) |
其中,k=(t./Kmax)+1,t为当前迭代步数,Kmax为模型中包含的最大块数,“./”表示取余数.在当前迭代步,根据公式(8)~公式(10)更新模型参数时,仅更新第k个块相关的参数;接着,与该块相关的参数变化信息讯速传递给下一个需要更新的块,这点不同于标准EM需要在全部块参数估计完成后才能将变化信息传递出去;最终实现CEMM算法的加速收敛.
上述过程为CEMM算法的参数估计过程,不具有模型选择能力,但具有一次只更新一个块相关参数特性的CEMM算法可以结合基于RSBM模型参数先验而推出的MML实现参数估计与模型选择的并行计算.
3.2.2 模型选择方法最小信息长度MML其原理是最优模型产生的数据有最短编码.设想网络N是由模型X依据P(N|X)生成,当进行传输时,通常需要对网络N与模型X一起编码.当利用MML作为模型选择准则时,认为数据编码长度与模型编码长度之和最小的模型即为最优模型.MML准则可具体表示如下:
| $\bar{h}=\arg \underset{h}{\mathop{\min }}\,\left\{ -\ln p(h)-\ln p(N|h)+\frac{1}{2}\ln |I(h)|+\frac{c}{2}\left( 1+\ln \frac{1}{12} \right) \right\}$ | (11) |
其中,$I(h)\equiv -E[D_{h}^{2}\ln p(N|h)]$表示Fisher信息矩阵,|I(h)|表示行列式,c表示参数h的维数.MDL准则与BIC准则
可以通过公式(11)近似获得.针对RSBM模型,本文引入RSBM模型参数的先验分布,推导出适用于RSBM模型的基于MML准则的成本函数,并基于该成本函数,结合CEMM算法实现参数估计与模型选择的并行计算.
首先,将Ω,Θ,
| $p(h)=p({{\omega }_{1}},...,{{\omega }_{k}})\prod\limits_{k=1}^{K}{p({{\theta }_{k}},{{\delta }_{k}})}$ | (12) |
| $p({{\omega }_{1}},...,{{\omega }_{k}})=|I(\Omega ){{|}^{\frac{1}{2}}}=\prod\limits_{k=1}^{K}{\omega _{k}^{-\frac{1}{2}}}$ | (13) |
| $p({{\theta }_{k}},{{\delta }_{k}})={{\left( \prod\limits_{j=1}^{n}{\theta _{kj}^{-1}(1-\theta )_{kj}^{-1}\delta _{kj}^{-1}(1-\delta )_{kj}^{-1}} \right)}^{\frac{1}{2}}}$ | (14) |
对于|I(h)|,因直接获取其表达式非常困难,我们采用完整数据的Fisher信息矩阵代替.因为其上界即|I(h)|,所以这是合理的.最终,针对RSBM模型,MML准则可重写为
| $\bar{h}=\arg \underset{h}{\mathop{\min }}\,\ell (h,N)$ | (15) |
其中,
| $\ell (h,D)=\frac{c}{2}\sum\limits_{k:{{\omega }_{k}}>0}^{K}{\ln \left( \frac{n{{\omega }_{k}}}{12} \right)}+\frac{{{K}_{nz}}}{2}\ln \frac{n}{12}+\frac{{{K}_{nz}}(c+1)}{2}-\ln p(N|h)$ | (16) |
其中,l(h,N)为成本目标函数;K表示模型的块数;wk表示块k的存在概率,即节点分配给块k的概率;c表示与每
个块相关的参数数量;Knz表示存在概率为非0的块数,亦即Ω中非零的元素个数;h表示模型参数(Ω,Θ,
成本目标函数(16)可以解释为:仅需编码那些存在概率不为0的块(wk0)的相关参数;当块的存在概率等于0(wk=0)时,指示该块未分配任何节点,可以直接销毁.目标函数中的wk反映了分配给块k的节点数,将此目标函数嵌入到CEMM算法的迭代过程中,通过最小化该成本函数获取各块的存在概率.在迭代过程中,通过不断地消毁存在概率等于0(wk=0)的块,可以实现边模型选择边参数估计,在算法的收敛过程中得到最优模型.
固定Knz,最小化目标函数(16)可得:
| $\bar{\omega }_{k}^{(t)}=\frac{\max \left\{ 0,\sum\nolimits_{i=1}^{n}{{{\gamma }_{ik}}}-\frac{c}{2} \right\}}{\sum\limits_{j=1}^{K}{\max \left\{ 0,\sum\nolimits_{i=1}^{n}{{{\gamma }_{ij}}}-\frac{c}{2} \right\}}}$ | (17) |
用公式(17)替换CEMM算法中M步中的公式(8),在M步,当$\bar{\omega }_{k}^{(t)}=0$时,其对应的块相关参数对观察数据的
似然没有任何贡献,可将该块消灭.上述算法的反复迭代,实现了模型选择与参数估计的并行计算.
3.2.3 RFLA算法给定网络N,RFLA学习算法见表 2.
| Table 2 RFLA learning algorithm 表 2 RFLA学习算法 |
为直观显示模型选择与参数估计的并行学习与串行学习的区别及其计算复杂度差别的原因,下面以人工网络为例展示算法在并行与串行策略下学习过程的不同.因现有SBM学习方法都采用串行方式进行模型选择与参数估计,选择GSMDL算法[7]为代表进行比较.实验网络利用Newman模型生成的人工网络.
该模型由Newman等人[17]提出,可用于生成社区结构网络,其定义为
| $Mode{{l}_{newman}}=\left( K,s,d,{{z}_{in}},{{z}_{out}} \right)$ | (18) |
其中,K表示生成网络的社区数目;s表示每个社区包含的节点数目;d表示每个节点的平均度,且d=zin+zout;zin和zout分别表示在社区内与社区间的边数.当zout增加时,相应的zin减少,正确地检测社区变得困难.
实验中,其参数设置为K=4,s=32,d=15,zout=2,生成节点总数为128的人工网络.两种算法都设置Kmin=2,Kmax=15,设置相同收敛条件.图 1(a)显示了RFLA算法的学习过程,其中:纵坐标为成本函数值,横坐标为迭代次数;实线表示算法在对应的迭代过程中消亡一个块;虚线表示在算法收敛后,检验是否存在应消亡而未被消亡的块,虚线为该迭代步强制消亡一个块.图 1(b)显示了GSMDL算法的学习过程,其纵坐标为成本函数值,横坐标为迭代次数,图中两虚线之间的迭代过程表示在K取某一值时算法的学习过程,K表示块数.通过图 1(a)可以看出: RFLA算法在参数学习的过程中不断消亡块,仅对好的模型进行参数估计.而从图 1(b)可以看到:GSMDL算法需要针对每个K值进行不断第迭代学习以确定K的最优值,因此需要更多的迭次次数.对比图 1(a)与图 1(b)可以明显看出:GSMDL需要消耗更多的计算成本寻找最优模型;而RFLA则将模型选择与参数学习结合到一起并行进行,有效地降低了计算复杂度.这是两类算法的主要区别及影响算法时间复杂度的主要原因.

|
(a) RFLA算法学习曲线 (b) GSMDL算法学习曲线 Fig. 1 Learning process of two type of algorithms 图 1 两类算法学习过程 |
3.2.4 时间复杂度
RFLA算法的时间复杂度主要由3部分决定:计算隐变量Z后验分布、估计参数(Ω,Θ,
本节利用人工合成网络与真实网络验证所提模型与算法的准确度与计算成本,并与同类算法进行对比分析;同时,对算法可处理的网络规模进行测试.另外还设计了链接预测实验,验证模型及其算法的泛化能力.本文所有算法都利用Matlab语言编写,运行在Dell计算机上,其中,CPU为双核2GH,内存4GB,操作系统为Window 7.
4.1 对比方法为了更好地表明所提模型和算法在准确性与计算成本方面的优势,我们选择不同的算法进行对比分析.表 3列出了现有具有模型选择能力的SBM学习算法,表中的I指不同算法收敛时所需的迭代次数.当已知块数K时,学习的时间复杂度指模型参数估计的时间复杂度;当K未知时,模型搜索的范围为从K=1到K=n(n指网络节点数),串行学习算法的时间复杂度为对模型空间中所有模型进行参数估计的开销之和.注意:我们在分析这些算法的时间复杂性时,注重分析算法的理论时间复杂性,而没有考虑通过采用某种程序设计技巧而导致节省的时间开销,如 ,稀疏网络可以邻接链表而非邻接矩阵的形式压缩存储.根据如下原则从表 3中选择出4种算法作为对比方法:选择的算法或者是经典SBM学习算法,或者是最新提出的SBM学习算法,或者是计算复杂度较低的SBM学习算法.
| Table 3 SBM learning algorithms 表 3 SBM学习算法 |
(1) VBMOD[12]:该算法采用变分贝叶斯方法进行参数估计及近似证据(evidence)进行模型选择.目前,VBMOD是计算复杂度最低的算法,但仅能分析只包含社区结构或者只包含多分结构的网络;
(2) SICL[11]:是针对标准SBM模型提出的具有模型选择能力的学习方法,其采用变分EM进行参数学习,利用ICL进行模型选择.该算法将变分首次应用于标准SBM中,也是首次将ICL模型选择准则应用于SBM中;
(3) GSMDL[7]:该算法是针对多尺度SBM提出的学习算法,采用EM算法进行参数学习,利用MDL选择模型;
(4) SILvb[13]:该算法是目前为止最新的具有模型选择能力的SBM学习方法,采用变分EM方法进行参数学习,利用ILvb进行模型选择.相对于SICL学习方法仅近似估计隐含变量的分布而对模型其他参数进点估计,SILvb对所有未知变量及参数利用变分近似其分布,这也是SILvb相对于现有SBM学习算法具有更好准确度的主要原因;
(5) RM[15]:该算法是基于混合模型的一类学习算法,尽管该算法没有模型选择能力,但其利用一个评价结构划分好坏的标准,可以确定块的数目.由于该模型可以描述块到节点的结构,同时,因该模型是Newman等人[4]提出模型的改进模型,比原模型性能更好,因此本文实验选择其作为对比算法.
4.2 人工网络验证 4.2.1 准确性验证为公平对比各算法的准确性,采用与文献[13]中相同的测试方法:利用SBM模型分别生成两类含有50个节点的人工网络,一类含有社区结构,另一类含有社区与多分的混合结构;每类网络由块数Qtrue分别为3,4,5,6,7的5组网络组成,每组随机生成100个网络.生成两类网络的参数设置如下.
(1) 对于社区结构,设置块内连接概率为0.9,块间连接概率为0.1;
(2) 对于社区与二分/多分混合结构:块数为3时,包含1个社区一个二分;块数为4时,包含2个社区与1个二分;块数为5时,包含2个社区与1个由3个块组成的多分;块数为6时包含3个社区与1个由3个块组成的多分;块数为7时包含3个社区与2个二分;其连接概率分别参照0.9与0.1进行设置.
表 4列出了6种算法在仅含有社区结构的人工网络上识别出的块数的混淆矩阵(confusion matrices).
| Table 4 Confusion matrices of detected blocks in networks with community 表 4 社区结构网络上识别块数的混淆矩阵 |
从表 4中可看到:当真实社区数目Qtrue<7时,VBMOD表现出良好的稳定性,对于小于7的每一个网络都能准确地发现社区结构;当Qtrue=7时,RFLA与SILvb的性能最好,分别可以识别出68个与83个社区;就整体性能而言,RFLA与SILvb是最好的.
表 5显示了6种算法在含有社区与多分结构的人工网络上识别出的块数的混淆矩阵.
| Table 5 Confusion matrices of detected blocks in networks with community and multipartite 表 5 社区与多分结构网络上识别块数的混淆矩阵 |
从表 5中可以明显看到:VBMOD算法无法胜任对这种网络结构的挖掘任务,性能表现最差,未能发现任何一个正确的网络结构;其他5种算法都能很好地发现网络的结构,特别是当Qtrue<7时,SILvb效果最好;当Qtrue=7时,SILvb依然表现出最好的性能,RFLA稍差于SILvb.
综合以上结果,可以得出以下结论.
(1) 块内节点包含的数目越少,挖掘出正确的结构越困难.当Qtrue=7时,算法的挖掘效果最差.原因在于块内的节点太少,平均每个块只有50/77.1;
(2) VBMOD算法相比其他算法在社区结构挖掘方面表现出很好的稳定性,但对于其他结构,其性能最差,错误估计的结构数目最多;
(3) SILvb的性能高于SICL,特别是在块内包含节点数目较少时.其原因在于两方面:一是ICL模型选择方法在选择模型方面不如ILvb模型选择方法;二是SILvb采用近似估计参数的后验分布,而SICL的参数估计方法则采用点估计;
(4) 我们提出RFLA在整体性能上稍差于SILvb,但明显优于其他3种算法.
4.2.2 计算时间比较为了更直观地了解各算法的计算复杂度,我们利用人工网络与真实网络测试各种算法的实际运行时间.本节设计3个实验:一是利用人工网络测试计算时间与计算准确度;二是利用人工网络测试计算成本与网络规模的关系;三利用足球队网络[17]测试模型空间规模[Kmin,Kmax]与计算成本的关系.
实验中,利用Newman模型生成不同规模的人工网络,利用标准互信息测量结构划分的准确程度.标准互信息(normalized mutual information,简称NMI)是一种常用的用于评价社区发现准确度的一种测度[18],NMI值越高,表明算法准确度越高;NMI值越低,表明算法准确度越低.实验中,利用NMI评价各算法的结构划分的正确性. Newman模型参数设置为K=4;s=32;d=16;zout分别取值为[1,…,8],生成8组网络,每组网络含10个网络.同时 ,生成网络时,对模型进行了简单的调整,使得网络包含两个社区与一个二分.对于二分,令zout表示节点在块内的边数.对于6种算法统一设置Kmin=2,Kmax=10及收敛阈值10-4进行结构发现.图 2(a)显示了6种算法NMI的平均值随zout值的变化曲线对比图.从图中可以看到:当zout值≤5时,RFLA,SICL与SILvb算法的NMI值为1,即,可以完全准确的识别出每个节点所属的块,表明RFLA具有较好的结构发现能力;而GMDL,VBMOD与RM算法的准确度明显低于RFLA,SICL与SILvb算法的准确度.同时,选择zout=4生成的网络进行计算时间测试,图 2(b)显示了6种算法的平均计算时间.从图中可以看出,RFLA的计算时间明显小于其他5种算法的计算时间.图 3的实验结果综合表明了提出的RFLA明显减少计算时间的同时仍具有较高的识别准确度.

|
(a) 互信息 (b) 计算时间 Fig. 2 Comparisons of performance of 6 algorithms 图 2 6种算法性能比较 |

|
(a) 计算时间与网络规模关系 (b) 计算时间与Kmax关系 Fig. 3 Comparisons of performance of 6 algorithms 图 3 6算法性能比较 |
接下来测试不同网络规模下,6种算法的计算成本.利用如下参数设置生成人工网络:K=4,d=16,zout=2,s分别取值100,200,300,400,500,600,700,800.对应每个s值,生成一组人工网络,随机生成8组不同规模大小的网络,每组包含20个网络.对每组网络进行结构挖掘,统计每种算法的平均运行时间,6种算法取相同的模型空间,即Kmin=1,Kmax=10,设置相同的收敛阈值10-4.图 3(a)显示了6种算法平 均计算时间的变化曲线,横坐标表示网络节点数目,纵坐标为以秒为单位的计算时间对数值.由于不同算法的计算时间差异过大,当以正常时间秒(s)作为纵坐标单位时,RFLA与VBMOD将贴近横坐标轴,而无法看出算法计算时间的变化,因此采用计算时间的对数值作为纵坐标单位,即ln(s).从图中可以看到:
· 提出的RFLA算法计算时间明显低于其他几种算法;
· VBMOD算法同样表现出其优势,原因在于:相对其他SBM至少为k2个链接参数,其链接参数仅为2个,参数的减少有效降低了其时间复杂度,属于典型的以精度换时间的学习算法.
· SICL与SILvb算法计算时间曲线在对数尺度下显示为重叠曲线,实际上,SILvb时间稍低于SICL,其主要原因在于两种算法采用了相同的模型.
理论上,当我们没有任何网络的先验知识时,K的可能取值范围为整个模型空间,即[1,…,n],n表示网络的节点总数.接下来的实验中,测试算法的计算成本与模型空间大小的关系.选择由115个节点组成的足球队网络[16]进行测试,设置Kmin=1,Kmax取值分别为10,20,30,40,50,60,70,80,90,100.图 3(b)显示了6种算法的计算时间随Kmax的变化曲线.从图中可以看出:RFLA具有最少的计算时间,明显低于其他算法.其原因在于:RFLA算法不需要对每一个模型都进行参数估计,而是直接对好的模型进行学习,在算法的迭代学习过程中,并行执行模型选择,直接丢弃不好的模型,减少对这些模型的估计成本.
为测试算法可处理的网络规模,利用Newman模型生成5组网络,每组网络都含有16个社区,每组网络的节点数与边数,见表 6.
| Table 6 Comparison of run time of RFLA and VBMOD (s) 表 6 RFLA与VBMOD算法计算时间比较 (s) |
由于受计算机及Matlab对内存空间的限制,测试的网络最大规模为包含2万个节点、200万条边的网络.设置算法参数Kmin=1,Kmax=30.实验中,仅选择目前最快的算法VBMOD进行对比.表 6显示了两种算法的平均运行时间.从表中可以看到,RFLA算法运行时间明显小于VBMOD算法的运行时间.对于2万节点的网络,RFLA仅需5 989s,而VBMOD则需要18 119s.表明当需要在K的某个取值范围内进行学习时,RFLA 显示出其低计算成本的优势.
4.2.3 模型与算法泛化能力的比较本节选取8个真实网络进一步验证算法处理真实网络的计算成本,同时,利用学习获得的参数值进行链接预测以测试各个算法的泛化能力.8个真实网络分别为俱乐部网络(karate)[17]、海豚网络(dolphins)[19]、政治图书同购网络(polbooks)(http://www.orgnet.com)、足球队网络(football)[17]、音乐网络(jazz)[20]、美国航空网络(usair)[21]、科学家协作网络(netscience)[22]、生物代谢网络(metabolic)[23].对于科学家协作网络,选择其最大连通子网络作为测试网络.表 7列出了8个网络的拓扑特征.
| Table 7 Topology characteristics of real networks 表 7 真实网络的拓扑特征 |
首先测试不同算法在具有不同拓扑特性的真实网络上的计算成本,并进行对比.设置Kmin=1,Kmax=n,n为网络的节点数.表 8列出了6种算法的计算时间,其中,“-”表示难以计算.通过表 8可以发现:RFLA算法的计算时间明显低于其他5种算法,其次是VBMOD,而SICL计算成本最高.对于分别含379,453个节点的Netscience与Metabolic网络,SICL,SILvb,GSMDL和RM算法已难以计算.
| Table 8 5种算法计算时间比较 (s) 表 8 Comparisons results of run time of 5 algorithms (s) |
接下来,利用学习获得的参数进行链接预测以测试对比模型与算法的泛化能力.实验中,对比算法除选择5个基于SBM的方法外,另选择基于共同邻居(common neighbors)相似指数(index)的预测算法(简称CN)[24]进行对比分析.CN算法利用两节点间所拥有的共同邻居数量预测节点间边出现的可能性,是用于验证链接预测方法性能优劣的常用基准方法.评价算法链接预测的性能通常采用准确度(precision)作为测度.给定有序的未观察到的链接集合,准确度定义为真实链接的数量与选择的链接的数量的比值,即:如果取前L个链接作为预测的链接,其中,Lr个链接是正确的,那么准确度值等于Lr/L.明显地,准确度值越高,意味着预测性能越好.
利用SBM模型进行链接预测,需要根据模型参数值确定节点间存在边的概率,然后,基于此概率进行预测.本文提出的随机块模型RSBM有P=ZQ,其中,Z表示隐变量矩阵,Q表示块到节点的连接概率矩阵,P表示节点间的连接概率.对于其他SBM模型,利用相应参数得到节点间的连接概率.对真实网络,首先按测试边的比例为0.1生成训练集与测试集,每个网络随机生成20组数据,然后,分别利用6种算法进行链路预测.表 9显示了各算法在L=10时预测结果的准确度均值及标准偏差.
| Table 9 Compared result of precision value of the algorithms in real networks (L=10) 表 9 链接预测方法对真实网络的准确度值比较(L=10) |
从表 9可以看出:相比其他算法,提出的模型与方法除netscience网络外,对每个网络都有最高的准确度值,表明其具有更好的链路预测能力;VBMOD算法预测结果最差;相比其他模型及方法,提出的模型及学习算法能捕获更多的网络结构信息,具有更好的泛化能力.
5 应 用相比社区发现方法,提出的方法,可以发现网络结构隐含的更多信息.下面以美国航空网络为例[21],说明RFLA算法的应用.美国航空网络基于1997年美国飞行航线数据构建,包含332个节点与2 126条边,节点表示机场,边表示两机场间有飞行航线.机场所处位置分布在美国本土、阿拉斯加州、夏威夷及西太平洋部分岛屿上.图 4(a)显示了对应于每个机场位置的美国航空网络结构图.
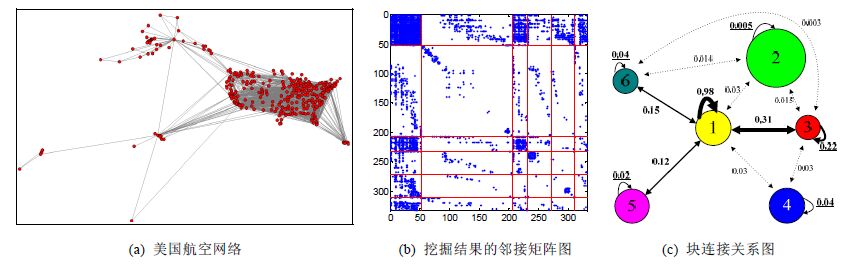
|
(a) 美国航空网络 (b) 挖掘结果的邻接矩阵图 (c) 块连接关系图 Fig. 4 Result of RFLA 图 4 RFLA算法挖掘结果 |
利用RFLA算法进行结构挖掘,算法共发现6个块.图 4(b)显示了根据节点所属块进行标签调整后的邻接矩阵.通过邻接矩阵图可直观的看到:块1与块3为内部紧密相连的块,其内部机场间航线较多,并且块1内部节点间的连接紧密程度明显高于块3节点的紧密程度;同时,块1与块3之间的连接也同样紧密;块2与块4可看作是边缘节点构成的块,其不仅内部连接稀疏而且与其他节点间连接也非常稀疏;块5与块6同样是内部连接相对稀疏的块,但不同于块2与块4,他们都与块1具有较紧密的连接关系.通过算法学习得到的参数,可计算出块内\间连接概率,利用块连接概率可以绘制出更加详细的能反应网络结构全局与局部特性的块连接图,如图 4(c)所示.图 4(c)中:每个圆对应于图 4(b)中的一个块,不同的颜色表示不同的块,圆的大小表示块内包含的节点数量的多少;圆上的带箭头的线表示块内节点间的连接概率,附近数字表示概率值,箭头的粗细与概率值大小相对应;圆间的箭头线表示块间连接概率;当块间连接概率非常小时,利用虚线表示块间连接.
通过图 4(c)的块连接图,可以直观地看出美国航空网络的全局结构特点与局部特点,即:整个网络可以看成由两个大的边缘节点块及一个由4个相互连接的块组成的网络;4个相互连接的块可以看作是网络的中心,而块1则可看作是4个连接块的中枢,该中枢块内部节点相比其他3个块的内部节点连接更加紧密;块3比块5、块6,与中枢块1的连接更加紧密.块连接图可提供更加直观准确的网络结构信息,基于这些信息能帮助合理调配航班.例如:当遇到客流高峰时,可以有选择地增加块1与块2、块3、块5、块6间的航班,避免成本浪费.
通过块-节点连接概率,可获得更详细的机场客流信息.图 5(a)显示了块1与块3内4个机场间的连接关系,4个机场分别是西雅图国际机场、波特兰国际机场、哥伦布国际机场和沙加缅度国际机场,连接概率分别为0.6216,0.2973,0.7027,0.2432.正如所看到的:上述4个机场尽管同属于块3,但每个机场与块1的连接概率不同.这反映了客流的不同,其中,哥伦布国际机场因地处美国中部而其他3个机场则处于美国西部,其客流高于其他3个国际机场.图 5(b)显示了块4内3个机场与块1、块3间的连接关系,3个机场分别为密洛特国际机场、斯波坎国际机场、潘伯恩纪念机场.正如所看到的:尽管3个机场同属块4,但与块1与块3的连接概率并不相同,表明提出的模型可更好地帮助分析航班客流特点.

|
(a) 块与同一块内不同节点间的关系 (b) 同一块内不同节点与不同块间的关系 Fig. 5 Relation of block-node connection 图 5 块-节点连接关系图 |
图 6显示了对不同块的节点按照相应的颜色进行着色后的美国航空网络,块1~块6分别着黄色、绿色、红色、蓝色、粉色与暗绿色.黄色节点,即中枢节点,主要分布在美国本土.位于中枢块内的机场通常是美国最繁忙的机场,如亚特兰大国际机场、达拉斯-福特沃斯国际机场、洛杉矶国际机场、芝加哥-奥黑尔国际机场等.地处夏威夷的瓦胡岛檀香山国际机场虽然不在美国本土,但因其处于世界闻名的旅游地点,而成为重要的中枢机场.位于边缘块2与块4的绿色、蓝色节点散布在美国领土的各个区域内,其中,块4与块2虽然同属边缘块,但块4内部连接相对块2较多;同时,块4节点主要分布在美国本土.这表明:虽然都处于边缘块内,美国本土的边缘机场的客流比本土外边缘机场的客流多.

|
Fig. 6 Colored USA airline according to blocks 图 6 节点着色后的美国航空网络 |
通过上述分析表明:利用RFLA对美国航空网络进行分析,可以在航空客流动向、合理调整设置航线、安全监管等方面提供有价值的信息.文献[25]利用社区挖掘算法分析了美国航空网络,挖掘得到3个社区,通过分析3个社区仅能得到机场的位置相关信息.相对社区挖掘算法,利用RFLA分析美国航空网络,能提供更多的精确信息.
6 结束语针对目前SBM学习方法(特别是具有模型选择能力的学习方法)普遍存在的计算复杂度高的问题,本文首先提出了一种精细随机块模型RSBM,进而从参数估计与模型选择两方面进行了研究,提出了一种面向RSBM模型的具有模型选择能力的快速学习方法.该方法采用边评价模型、边估计参数的策略,并行参数估计与模型选择,以此方式显著减低学习的时间复杂性.本文提出并实现了参数估计与模型选择并行进行的SBM并行学习算法.为验证算法的性能,我们利用人工网络与真实网络对算法的准确性与计算成本进行了测试,并与现有具有模型选择能力的学习算法进行了比较,实验结果表明:对于无任何先验知识的网络,提出的算法在保持与现有最好算法学习准确度基本相同的条件下,明显降低了学习过程的计算复杂度,使得具有模型选择能力的SBM学习算法能有效处理的网络规模从几百节点提高到几万节点;同时,通过链接预测实验表明,提出的随机块模型和学习算法具有良好的泛化能力.后续工作中,我们将研究参数估计的近似算法和多处理器环境下分布式并行实现,进一步降低SBM学习算法的时间复杂性,使之能处理更大规模的真实网络.
致谢 本文主要工作在吉林大学计算机学院和吉林大学符号计算与知识工程教育部重点实验室完成,在此表示感谢.| [1] | Holland PW, Laskey KB, Leinhardt S. Stochastic blockmodels:First steps. Social Networks, 1983, 5 (2) :109–137. [doi:10.1016/0378-8733(83)90021-7] |
| [2] | Airoldi EM, Blei DM, Fienberg SE, Xing EP. Mixed membership stochastic blockmodels. The Journal of Machine Learning Research, 2008, 9 :1981–2014. http://cn.bing.com/academic/profile?id=2107107106&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | Latouche P, Birmelé E, Ambroise C. Overlapping stochastic block models with application to the french political blogosphere. The Annals of Applied Statistics, 2011, 5 (1) :309–336. [doi:10.1214/10-AOAS382] |
| [4] | Newman MEJ, Leicht EA. Mixture models and exploratory analysis in networks. Proc.of the National Academy of Sciences of the United States of America, 2007, 104 (23) :9564–9569. [doi:10.1073/pnas.0610537104] |
| [5] | Karrer B, Newman MEJ. Stochastic blockmodels and community structure in networks. Physical Review E, 2011, 83 (1) :016107. [doi:10.1103/PhysRevE.83.016107] |
| [6] | Yang T, Chi Y, Zhu S, Gong Y, Jin R. Detecting communities and their evolutions in dynamic social networks-A Bayesian approach. Machine Learning, 2011, 82 (2) :157–189. [doi:10.1007/s10994-010-5214-7] |
| [7] | Yang B, Liu JM, Liu DY. Characterizing and extracting multiplex patterns in complex networks. IEEE Trans.on Systems Man and Cybernetics,Part B-Cybernetics, 2012, 42 (2) :469–481. [doi:10.1109/TSMCB.2011.2167751] |
| [8] | Snijders TA, Nowicki K. Estimation and prediction for stochastic blockmodels for graphs with latent block structure. Journal of Classification, 1997, 14 (1) :75–100. [doi:10.1007/s003579900004] |
| [9] | Shen HW, Cheng XQ, Guo JF. Exploring the structural regularities in networks. Physical Review E, 2011, 84 (5) :056111. [doi:10.1103/PhysRevE.84.056111] |
| [10] | Decelle A, Krzakala F, Moore C, Zdeborova L. Inference and phase transitions in the detection of modules in sparse networks. Physical Review Letters, 2011, 107 (6) :065701. [doi:10.1103/PhysRevLett.107.065701] |
| [11] | Daudin JJ, Picard F, Robin S. A mixture model for random graphs. Statistics and Computing, 2008, 18 (2) :173–183. [doi:10.1007/s11222-007-9046-7] |
| [12] | Hofman JM, Wiggins CH. Bayesian approach to network modularity. Physical Review Letters, 2008, 100 (25) :258701. [doi:10.1103/PhysRevLett.100.258701] |
| [13] | Latouche P, Birmele E, Ambroise C. Variational Bayesian inference and complexity control for stochastic block models. Statistical Modelling, 2012, 12 (1) :93–115. [doi:10.1177/1471082X1001200105] |
| [14] | Figueiredo MAT, Jain AK. Unsupervised learning of finite mixture models. IEEE Trans.on Pattern Analysis and Machine Intelligence, 2002, 24 (3) :381–396. [doi:10.1109/34.990138] |
| [15] | Ramasco JJ, Mungan M. Inversion method for content-based networks. Physical Review E, 2008, 77 (3) :036122. [doi:10.1103/PhysRevE.77.036122] |
| [16] | Celeux G, Chretien S, Forbes F, Mkhadri A. A component-wise EM algorithm for mixtures. Journal of Computational and Graphical Statistics, 2001, 10 (4) :697–712. [doi:10.1198/106186001317243403] |
| [17] | Girvan M, Newman MEJ. Community structure in social and biological networks. Proc.of the National Academy of Sciences of the United States of America, 2002, 99 (12) :7821–7826. [doi:10.1073/pnas.122653799] |
| [18] | Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure in complex networks. New Journal of Physics, 2009, 11 (3) :033015. [doi:10.1088/1367-2630/11/3/033015] |
| [19] | Lusseau D, Schneider K, Boisseau OJ, Haase P, Slooten E, Dawson SM. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations-Can geographic isolation explain this unique trait?Behavioral Ecology and Sociobiology,2003,54(4):396-405. Behavioral Ecology and Sociobiology, 2003, 54 (4) :396–405. [doi:10.1007/s00265-003-0651-y] http://cn.bing.com/academic/profile?id=2094234423&encoded=0&v=paper_preview&mkt=zh-cn |
| [20] | Gleiser PM, Danon L. Community structure in jazz. Advances in Complex Systems, 2003, 6 (4) :565–573. [doi:10.1142/S0219525903001067] |
| [21] | Batageli V,Mrvar A.Pajek datasets.http://vlado.fmf.uni-lj.si/pub/networks/data/default.htm |
| [22] | Newman MEJ. Finding community structure in networks using the eigenvectors of matrices. Physical Review E, 2006, 74 (3) :036104. [doi:10.1103/PhysRevE.74.036104] |
| [23] | Duch J, Arenas A. Community detection in complex networks using extremal optimization. Physical Review E, 2005, 72 (2) :027104. [doi:10.1103/PhysRevE.72.027104] |
| [24] | Lü L, Jin CH, Zhou T. Similarity index based on local paths for link prediction of complex networks. Physical Review E, 2009, 80 (4) :046122. [doi:10.1103/PhysRevE.80.046122] |
| [25] | Ball B, Karrer B, Newman MEJ. Efficient and principled method for detecting communities in networks. Physical Review E, 2011, 84 (3) :036103. [doi:10.1103/PhysRevE.84.036103] |
 2016, Vol. 27
2016, Vol. 27


