圆形Packing问题是高复杂度典型的NP难度问题,在无线通信、航空航天及交通运输等领域均有着广泛的应用.随着问题规模的增大,问题的解空间呈指数级膨胀,使得精确算法的求解时间过长而不适于实际应用.国内外研究者多采用启发式方法求解此类问题,如拟物算法[1, 2]、禁忌算法[3, 4]、模拟退火算法[4, 5, 6]、梯度下降算法[7]、遗传算法[8]等.其中,拟物法通过在自然世界中寻找与原始问题等价的物理现象,如模拟弹性物体在弹性力作用下的运动过程,从而设计得到一种高效率的求解算法.通常使用拟物法进行局部搜索,并采取拟人策略跳出局部极小值的陷阱.而如何快速、有效地找到当前格局下的最空闲空间以使搜索过程跳到更有前景的区域去是设计跳坑策略的一个关键难点.
本文研究圆形Packing问题的重要扩展问题——带平衡约束的圆形Packing问题.该问题在圆形Packing问题的基础上引入了静平衡约束,是以卫星舱布局为背景的全局优化问题.相关的求解方法包括模式迭代法和主布模法[9]、遗传算法[10, 11]、拟物算法[12]、粒子群优化算法[13, 14]、快速局部搜索算法[15]、散射搜索法[16]、吸引盘填充算法[17]、模拟退火算法[18]、基于禁忌搜索的启发式算法[19]和基于粗精调的拟物拟人算法[20]等.这些求解算法大致可以分为两类:一类是具有较强全局搜索能力及较高普适性的算法,如粒子群算法、散射搜索法、遗传算法等.另一类是具有较好局部搜索能力及较强针对性的算法,如拟物算法、快速局部搜索算法、吸引盘填充算法等.由于前者的局部搜索速度较慢,而后者容易落入局部极小点的陷阱,研究者通常将两类算法 结合起来以兼顾全局搜索能力和局部搜索速度.对于圆形Packing问题,目前已经有比较成熟的拟物模型[1, 2].而对于带平衡约束的圆形Packing问题,研究者多通过在圆形Packing问题的弹力模型的基础上引入静不平衡势能来构造势能函数[15, 16, 17, 18, 19],但未给出针对静平衡约束的贴切的拟物模型.2013年,何琨等人[20]引入了拉力模型以处理静平衡约束并取得了很好的效果.
本文以文献[20]提出的弹力模型和拉力模型为基础,将拟物法与3个拟人辅助策略相结合,提高了算法的全局搜索能力和局部搜索速度.当计算落入局部极小点的陷阱时,借鉴求解矩形Packing问题的动作空间[21, 22, 23, 24]的概念,通过化“圆”为“方”,将外包络圆和各圆饼近似看作矩形,从而使跳坑过程能够较快、较准确地找到当前格局下的最空闲空间,并结合一些拟人跳坑策略[4, 20],使搜索过程快速有效地离开局部极小点并跳到更有前景的区域中去.对目前国内外公开的13个代表性算例进行了计算.实验结果表明,所提算法是求解带平衡约束的圆形Packing问题的一种快速而有效的算法.
1 问题描述在设计人造卫星舱时,需要将若干圆柱形部件(待布物)互不嵌入地竖直置入舱体内,要求给出待布物的一种紧密布局,使得卫星舱的半径尽可能的小.同时,为了减小卫星舱自旋时产生的震动、噪音、发热等,要求布局后卫星舱的静不平衡量也尽可能的小,即要求所有待布物的重心尽可能接近整个舱体的中心.以卫星舱的一个横截面为研究对象,则上述问题可抽象为一个带平衡约束的二维圆形Packing问题:已知n个实心圆饼(n为任意正整数),圆饼Ci(i∈{1,2,…,n})的半径为ri、质量为mi,要求给出这n个圆饼的一种无嵌入的紧密布局,使得其外包络圆C0的半径R0 尽可能地小,且整个圆饼系统的质心与原点即外包络圆圆心的距离小于一个小的正实数dr.
问题可形式化地定义如下:以外包络圆的圆心为原点建立笛卡尔坐标系,设圆饼Ci的圆心坐标为(xi,yi),要求给出一个布局X=(${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}},...,{{x}_{n}},{{y}_{n}}$),使得:
min R0
s.t. (1) $d({{C}_{i}},{{C}_{0}})\triangleq \sqrt{x_{i}^{2}+y_{i}^{2}}\le {{R}_{0}}-{{r}_{i}}$,$i\in \left\{ 1,2,...,n \right\}.$
(2) $d({{C}_{i}},{{C}_{j}})\triangleq \sqrt{{{\left( {{x}_{i}}-{{x}_{j}} \right)}^{2}}+{{\left( {{y}_{i}}-{{y}_{j}} \right)}^{2}}}\ge {{r}_{i}}+{{r}_{j}}$,$i,j\in \left\{ 1,2,...,n \right\},i\ne j.$
(3) ${{R}_{c}}\triangleq \frac{\sqrt{{{\left( \sum\limits_{i=1}^{n}{{{m}_{i}}{{x}_{i}}} \right)}^{2}}+{{\left( \sum\limits_{i=1}^{n}{{{m}_{i}}{{y}_{i}}} \right)}^{2}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}}<{{\delta }_{r}}.$
在约束(1)中,d(Ci,C0)表示圆饼Ci的圆心到外包络圆C0的圆心的距离,即要求任意圆饼均完全落在外包络圆内.在约束(2)中,d(Ci,Cj)表示两圆饼Ci与Cj的圆心之间的距离,即要求任两圆饼互不嵌入.在约束(3)中,Rc为圆饼集的质心到原点的距离,当Rc<δr时,系统的静不平衡量$J=\left( \sum\limits_{i=1}^{n}{{{m}_{i}}} \right)\cdot {{R}_{c}}$小于${{\delta }_{J}}\triangleq \left( \sum\limits_{i=1}^{n}{{{m}_{i}}} \right)\cdot {{\delta }_{r}}$.
在上述问题定义中,由于R0不确定,其直接求解的难度较大.本文拟先求解此问题的判定形式,即对给定的R0,要求判定是否存在一种布局方案同时满足上述3个约束;然后利用二分法不断迭代,就可找到原问题的一个使R0较小的解.因此,只需讨论问题的判定形式下的拟物模型和求解策略.
2 拟物模型对于带平衡约束的圆形Packing问题,文献[20]提出了两个物理模型:弹力模型和拉力模型.
2.1 弹力模型将n个圆饼想象为光滑的弹性实体,将外包络圆想象为一刚性容器,根据弹性力学,这n个圆饼在容器中相互挤压时会受到弹性力的作用并产生弹性势能,由此设计得到相应的弹力模型.
将外包络圆编号为物体0,将圆饼Ci(i{1,2,...,n})编号为物体i.在任意时刻,设圆饼Ci(i{1,2,...,n})的圆心坐标为(xi,yi),称2n元组X=(${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}},...,{{x}_{i}},{{y}_{i}}$)为一个格局.
对给定格局X,系统的总弹性势能Ue(X)见式(1).
| ${{U}_{e}}(X)={{k}_{e}}\cdot \sum\limits_{j=0}^{n-1}{\sum\limits_{i=j+1}^{n}{D_{ij}^{2}}}$ | (1) |
其中,ke表示圆饼的弹性系数,Dij表示两物体i和j之间的嵌入深度,见式(2).
| ${{D}_{ij}}=\left\{ \begin{align} &\max \left( 0,{{r}_{i}}+{{r}_{j}}-d\left( {{C}_{i}},{{C}_{j}} \right) \right),\text{ }i,j\in \left\{ 1,2,...,n \right\},i\ne j \\ &\max \left( 0,{{r}_{i}}-{{R}_{0}}+d\left( {{C}_{i}},{{C}_{0}} \right) \right),\text{ }i\in \left\{ 1,2,...,n \right\},j=0 \\ \end{align} \right.$ | (2) |
可见,系统的总弹性势能与圆饼的嵌入深度正相关,当且仅当Ue(X)=0时,各物体互不嵌入,相应的格局满足约束(1)和约束(2).
2.2 拉力模型将圆饼集视为一个质点,想象该质点与原点之间有一根很紧的橡皮筋相连,当该质点与原点不重合时,将受到橡皮筋的拉力作用,此时系统存在偏移势能,由此设计得到相应的拉力模型.
对给定格局X,系统的偏移势能Uc(X)见式(3).
| ${{U}_{c}}(X)={{k}_{c}}\cdot \sqrt{{{{\bar{X}}}^{2}}+{{{\bar{Y}}}^{2}}}$ | (3) |
其中,kc为橡皮筋的拉力系数,$\left( \bar{X},\bar{Y} \right)$为圆饼集质心的坐标,见式(4).
| $\left( \bar{X},\bar{Y} \right)=\left( \frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}},\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{y}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}} \right)$ | (4) |
质心$\left( \bar{X},\bar{Y} \right)$到原点的距离即为Rc.当且仅当Uc(x)<kc·δr时,Rc<δr,相应的格局X满足约束(3).
综合弹力模型和拉力模型,对给定格局X,系统的总体势能U(X)见式(5).
| $U(X)={{U}_{e}}(X)+{{U}_{c}}(X)$ | (5) |
当U(X)>0时,说明各圆饼仍存在嵌入或系统未达到平衡状态.因此,对外包络圆半径给定的判定问题的求解转化为对U(X)最小的格局的求解.
3 拟物算法本节给出外包络圆半径给定的判定问题的求解算法,包括基于弹力模型和拉力模型的拟物下降算法、基于动作空间的拟人跳坑策略和两者相结合的完整拟物算法.拟物算法的基本思路是:从t=0时刻开始,随机生成一个初始格局,然后采用拟物下降法收敛至局部最优格局;若此时系统的总体势能大于0,即所得格局为非法格局,则执行拟人跳坑策略,从而得到新的格局;如此不断迭代,直至找到合法的解格局成功停机或达到规定时限强制失败停机.
3.1 拟物下降算法拟物下降法是一种高效的连续优化方法,其基本思路是:在t时刻对给定的格局X,若各圆饼所受的弹性合力大于0或圆饼集质心所受的拉力大于0,则各圆饼在弹性力和拉力作用下进行一次移动,从而得到t+1时刻的新格局X;如此不断迭代,直至找到局部最优格局停止移动.在整个拟物过程中,系统的总体势能呈下降的趋势.
在t时刻对给定格局X,让各圆饼在弹性力、拉力或两者合力的作用下进行一次移动如式(6)、式(7)或式(8)所示,分别称为弹力动作、拉力动作和综合动作.
| $\vec{r}_{i}^{(t+1)}=\vec{r}_{i}^{(t)}+{{h}_{e}}\cdot \vec{F}_{i}^{(t)},\text{ }i\in \left\{ 1,2,...,n \right\}$ | (6) |
其中,$\vec{F}_{i}^{(t)}$为t时刻圆饼Ci所受的弹性合力,$\vec{r}_{i}^{(t)}$为t时刻圆饼Ci的位置;he为弹性力作用下的移动步长.
| $\vec{r}_{i}^{(t+1)}=\vec{r}_{i}^{(t)}+{{h}_{c}}\cdot \vec{F}_{c}^{(t)},\text{ }i\in \left\{ 1,2,...,n \right\}$ | (7) |
其中,$\vec{F}_{c}^{(t)}$为t时刻圆饼集质心所受的拉力,hc为拉力作用下的移动步长.
| $\vec{r}_{i}^{(t+1)}=\vec{r}_{i}^{(t)}+{{h}_{e}}\cdot \vec{F}_{i}^{(t)}+{{h}_{c}}\cdot \vec{F}_{c}^{(t)},\text{ }i\in \left\{ 1,2,...,n \right\}$ | (8) |
定义1(卡壳格局). 若圆饼作一次移动后对任意Ci(i{1,2,...,n})均有$\vec{r}_{i}^{(t+1)}=\vec{r}_{i}^{(t)},$则称相应的格局X为卡壳格局.
带平衡约束的圆形Packing问题需综合考虑连续优化和组合优化两个因素.问题的解空间是连续的,核心困难源自其复杂的组合特征,即局部极小点的数量会随着圆饼数的增加而迅速膨胀.对于解空间中大量的局部极小点,只有少量甚至唯一的全局最小点.如果对每个搜索区域都严格执行拟物下降计算直至该区域的最小点,势必要消耗大量的计算时间.本文将拟物法与以下3个拟人辅助策略相结合以提高拟物下降的效率.
(1) 提前中止策略
在问题解空间大范围的搜索区域中,有些区域的局部极小点附近总体势能较大,称为无前景区域.在拟物过程中,由于早期势能的下降梯度较大,通常经过较少次迭代后各圆饼的相对位置就基本确定,如果此时总体势能仍然较大,则认为该搜索区域找不到问题的解,应尽早离开.同时,若当前格局的总弹性势能较小但偏移势能较大,则认为该格局无法收敛至解格局,应停止拟物计算.
具体做法是:(a) 在整个拟物计算过程中,记录下总弹性势能最小的格局Xbest.从当前格局X出发迭代15次,得到新格局X,若Ue(X)>Ue(Xbest)且Ue(X)>1,则提前中止对该区域的搜索.(b) 在拟物过程中对当前格局X,若Ue(X)≤10-10但Uc(X)>10-6,则停止计算.
(2) 粗精调策略
在拟物过程中,若当前格局的总体势能较大,则各圆饼的相对位置较不稳定,弹性力起主导作用.当计算接近局部极小点时,总体势能的收敛速度较慢,为了不在无前景区域的局部极小点附近花费过多时间,同时又不错过有前景的搜索区域,文献[20]将拟物算法分成粗调和精调两个阶段:对给定格局X,若Ue(X)>10-10,则进行弹力粗调,各圆饼执行弹力动作,直至Ue(X)≤10-10.若此时U(X)>10-10,则进行拉力粗调,各圆饼执行一次拉力动作.每次进行弹力粗调后就重新进行拉力粗调,直至总体势能足够小才进入精调阶段.
通过实验发现,若在某区域的搜索过程连续多次进入拉力粗调阶段,则可以预测其最终将进入精调阶段.为减少计算量,若U(X)≤10-10或在该区域的搜索过程连续3次进入拉力粗调阶段,则进行精调,各圆饼执行综合动作.在整个粗精调过程中,若当前格局为卡壳格局或满足提前中止条件,则停止拟物下降计算并跳坑.
(3) 自适应步长策略
在拟物过程中,移动步长的大小对计算的收敛速度影响甚大.由于初始阶段圆饼的嵌入深度相对较大,将ke和he的初始值设置为稍大于1的值,可以加快计算的收敛速度.因此,设置ke=1.2,he=1.2.同时,将hc的初始值设置为1,使得经过一次拉力调整后,圆饼集的质心刚好与外包络圆的圆心重合以尽快满足静平衡约束.当计算接近局部极小点时,若移动步长太大,将导致移动过量,使搜索在两个或多个格局之间来回振荡.因此,在圆饼的每次移动后,根据总体势能的变化情况动态调整下一轮迭代的移动步长[20].对当前格局X进行一次迭代后得到新格局X,若Ue(X)>Ue(X),则将he减小15%;若Uc(X)>Uc(X),则将hc减小5%.
使用上述方法进行多次调整后,可能使移动步长变得太小而导致收敛速度变得极慢.因此,若连续50次迭代中,Ue(X)都小于Ue(X),则将he和hc恢复到初始值.
在实际计算中,由于受到计算机的精度限制,无法使总体势能严格地降至0,因此,约定总体势能小于10-20时即可成功停机.设置kc=10-8,dr=10-12,则停机时Uc(x)<kc·dr=10-20.基于上述辅助策略,拟物下降算法(quasi- physical descent algorithm,简称QPD)的描述见算法1.
算法1.
输入:当前格局X;最好格局Xbest;
输出:拟物中止格局X.
1 弹力粗调阶段连续迭代次数l←0;
2 ke=1.2;kc=10-8;dr=10-12;he=1.2;hc=1.0;
3 while true do
4 计算总势能U(X);
5 if U(X)<10-20 then
6 return X; //返回格局X,成功退出;
7 end if
8 while U(X)>10-10 do //弹力粗调
9 计算每个圆饼的弹性合力,执行弹力动作,得到新格局X;
10 l++;
11 自适应调整步长;
12 X=X;
13 if (l>15 and Ue(X)>1 and Ue(X)>Ue(Xbest)) or 卡壳 then
14 returnX; // 提前中止策略(a)及卡壳中止
15 end if
16 end while
17 if Ue(X)<10-10 and U(X)>10-10 and l<3 then //拉力粗调
18 if Uc(X)>10-6 then
19 return X; //提前中止策略(b)
20 else
21 计算系统的拉力,执行拉力动作,得到新格局X;
22 X=X;
23 end if
24 l←0;
25 else if Ue(X)<10-10 //精调
26 while U(X)>10-20 do
27 if Uc(X)<kc·dr then
28 计算每个圆饼的弹性合力,执行弹力动作,得到新格局X;
29 else
30 计算每个圆饼的弹性合力及系统的拉力,执行综合动作,得到新格局X;
31 end if
32 自适应调整步长;
33 X=X;
34 if 卡壳 then
35 returnX; //卡壳中止
36 end if
37 end while
38 l←0;
39 end if
40 end while
41 return X
3.2 拟人跳坑策略当拟物计算落入局部极小点的陷阱时,研究者多使用拟人策略进行跳坑.常用的方法有两种:一是按一定的规则选择两个圆饼互换位置.这种方法对不等圆Packing问题效果较好,但在求解等圆Packing问题时由于互换的两圆饼等大,格局未发生任何变化,没有达到跳坑的目的.另一种方法是挑出当前格局中受挤压较严重的一至多个圆,并重新随机放入空腔内以打破僵局.此策略不仅能使计算跳出局部极小点的陷阱,且能保留计算过程中积累的有用信息,但随机性较大,对于一些难解的问题,由于搜索空间非常大,让圆饼跳到合适位置上的概率较低.因此,如何找到更贴切的拟人策略以提高跳坑的效率,宣泄大量的选择过程中搜索空间的膨胀,是提高算法的全局搜索能力的一个关键难点.
观察日常生活中的一些现象,如在拥挤的公共汽车上,受挤压最严重的人通常会设法往车上最宽松的地方移动.受此乘车现象的启发设计得到以下跳坑策略:当搜索落入局部极小点的陷阱时,挑出受挤压最严重的若干圆饼,将其重新放置到当前格局下最空闲的若干区域.通过观察发现,半径较大的圆饼的位置相对比较固定,而半径较小的圆饼的位置相对比较灵活,因此,让小圆饼有更多的跳坑机会.用相对痛苦度来评价系统中圆饼的受挤压程度.
定义2(相对痛苦度). 圆饼Ci(i{1,2,...,n})的相对痛苦度见式(9).
| ${{P}_{i}}=\frac{\sum\limits_{j=0,j\ne i}^{n}{D_{ij}^{2}}}{r_{i}^{2}}$ | (9) |
当总体势能较大时,说明有多个圆饼受到较严重的挤压,选出相对痛苦度最大的几个圆饼进行跳坑;当总体势能接近0时,各圆饼嵌入程度已经很小,故只选择出相对痛苦度最大的一个圆饼进行跳坑.
由于外包络圆中的空闲空间为不规则区域,直接计算其面积或周长都很困难.本文借鉴求解矩形Packing问题的拟人算法中动作空间[21, 22, 23, 24]的概念,通过化“圆”为“方”,将不规则的空闲空间近似为一系列规则的、容易计算的矩形空间,从而以较快的速度、较准确地找出给定格局下外包络圆中的最空闲区域.
定义3(动作容器G0). 如图 1所示,将外包络圆近似为两个矩形空间abcd和efgh的并集,称为动作容器G0. 其中,ab=ef=$\sqrt{2}$R0,ad=eh=2R0.G0关于原点对称.
定义4(动作矩形块Gi). 将圆饼Ci(i{1,2,...,n})近似转换为动作矩形块Gi,如图 1中阴影区域所示.为了更好地近似圆饼,取Gi的边长为Ci的外接矩形和内接矩形边长的平均值,即$\left( 1+\frac{\sqrt{2}}{2} \right)\cdot {{r}_{i}}$.
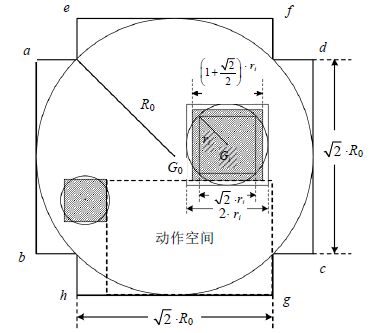
|
Fig. 1 An example of squaring the circles 图 1 化圆为方示意图 |
定义5(动作空间). 在当前格局下,往容器的剩余空间中放入一个尽可能大的虚拟矩形块,使其上、下、左、右4条边均与动作矩形块Gi或动作容器G0的边相贴(即重合的长度大于0),将该虚拟矩形块所占的空间称为一个动作空间.
图 1给出了一个动作空间的示例.
往一个动作空间中放入一个动作矩形块后,若该矩形块所占的区域与原动作空间的k条边相交(k{0,1,...,4}),则原动作空间被破坏,生成4-k个新的矩形空间,如图 2所示.
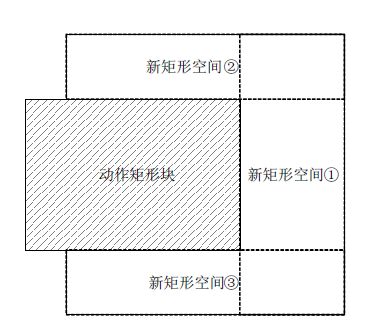
|
Fig. 2 An example of updating action spaces 图 2 动作空间的更新(k=1) |
计算给定格局下的所有动作空间的具体过程可描述如下:
步骤1. 初始化.
将外包络圆近似为两个矩形空闲空间,作为初始动作空间集合S.
将待置入的圆饼集合近似为动作矩形块集合G.
步骤2. 对每个动作矩形块Gi{
对每个动作空间Sj{
若Gi与Sj重叠,则把Sj从S中删除,并把更新后的动作空间添加到S中.
}}
最终得到的S集即所有动作空间.
定义6(空闲度). 对给定的一个动作空间,其空闲度见式(10).
| $空闲度=\left\langle 短边长,长边长,中点横坐标,中点纵坐标,宽长 \right\rangle $ | (10) |
两个动作空间空闲度的比较即按字典序比较各项的值.例如,若动作空间Sa的空闲度为á3,4,0,1,3,动作空间Sb的空闲度为á3,4,1,0,4,则Sa比Sb空闲.
为了避免重复搜索,在设计跳坑策略时结合了禁忌方法.具体做法为:设定一个禁忌表,若某个圆饼连续3次被选中,则将其加入禁忌表中并设置其禁忌长度为3,同时将表中其他圆饼的禁忌长度减1.若表中某个圆饼的禁忌长度减至0就将其解禁并从表中删除.为了提高算法的全局搜索能力,在每次跳坑时,依次按如下策略生成多个新的格局作为下一轮拟物搜索的起点.
(1) 挑出相对痛苦度最大且未被禁忌的圆饼,分别将其圆心置于空闲度最大和次大的动作空间的中心.
(2) 若U(X)>1,则挑出相对痛苦度最大且未被禁忌的两个圆饼,分别将其圆心置于空闲度最大和次大的动作空间的中心.
(3) 挑出相对痛苦度最大且未被禁忌的圆饼,将其圆心置于随机选取的一个动作空间的中心.
其中,前两个策略的针对性较强,可能使算法迂回于某些区域,因此加入了随机性较强的第3个策略.
3.3 QPAS算法综合上述拟物下降算法和基于动作空间的拟人跳坑策略,完整的基于动作空间的拟物算法(quasi-physical algorithm based on action space,简称QPAS)可描述见算法2.
算法2.
输入:运行时间上限L;
输出:最好格局Xbest.
1 随机生成m个格局;
2 运行时间t←0;
3 while t<L do
4 当前最好格局Xbest←;
5 for i←0 to m do
6 对第i个格局Xi执行QPD算法,得到格局${{{X}'}_{i}}$;
7 if $U\left( {{{{X}'}}_{i}} \right)$<10-20 then
8 return ${{{X}'}_{i}}$; //成功退出
9 end if
10 if ${{U}_{e}}\left( {{{{X}'}}_{i}} \right)$<Ue(Xbest) or Xbest== then
11 ${{X}_{best}}\leftarrow {{{X}'}_{i}}$;
12 end if
13 end for
14 对Xbest进行拟人跳坑,得到m个新格局;
15 end while
16 return Xbest
4 计算结果与分析本文将QPAS算法用C++语言编程实现,并在CPU主频为2.80 GHz、内存为4 GB的PC机上对3组共13个国际上公开的代表性算例进行了计算.第1组算例共5个,分别于1994年、1999年和2001年由滕弘飞等人[9, 10, 11]提出,并于2010年由刘景发和李刚[17]进行了汇总.第2组算例共6个,于2006年由黄文奇等人[12]提出.这两组算例 的具体数据见文献[17].
假设各圆饼均为单位厚度且密度均匀,物体的质量正比于其半径的平方.据此对文献[4]中的规模较大的两个算例进行转换,形成第3组算例,以进一步检验QPAS的性能.第3组算例见表 1.
| Table 1 The third set of instances 表 1 第3组算例 |
对每个算例均独立计算5次,取其中最小的外包络圆半径R0和相应的静不平衡量J,并计算5次的平均耗时T(s).主要用外包络圆的半径来衡量计算结果的优劣.对于第1组算例,表 2给出了QPAS与国内外文献中的代表性算法MPSO[13]、APSO[14]、IQP[12]、ISS[16]、BF[17]、HSA[18]、TSH[19]和QPCFA[20]的计算结果比较.在9种代表性算法中,QPAS有一个算例找到了更小的外包络圆半径,其布局坐标见表 3,布局图如图 3所示;有两个与当前的最好记录持平,另有两个排名第2.在9种算法中,IQP、ISS、HSA、TSH、QPCFA和QPAS都基于黄文奇等人[2]提出的能量函数进行优化,并在能量函数足够小时停机.其中,IQP和ISS的停机条件分别是U(X)<10-6和U(X)<10-8,而HSA、TSH、QPCFA和QPAS的停机条件是U(X)<10-20,停机精度远高于前者,因此前者有可能得到更小的外包络圆半径.
| Table 2 Computing results on the first set of instances 表 2 第1组算例计算结果比较 |
| Table 3 The detailed coordinates of the disks for instance 1.4 表 3 QPAS在算例1.4上的布局坐标 |
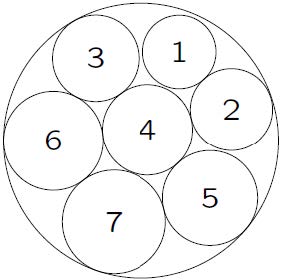
|
Fig. 3 Packing layout of instance 1.4 图 3 算例1.4 的布局图 |
对于第2组算例,由于提出的时间晚于第1组,目前只见IQP[12]、HSA[18]、TSH[19]和QPCFA[20]这4种算法对其进行了计算,表 4给出了计算结果的比较.在这5种算法中,QPAS有2个算例找到了更小的外包络圆半径,其布局坐标见表 5和表 6,布局图如图 4和图 5所示;有3个持平于当前的最好记录,另有1个略弱于何琨等人[20]于2013年最新报道的结果.
| Table 4 Computing results on the second set of instances 表 4 第2组算例计算结果比较 |
| Table 5 The detailed coordinates of the disks for instance 2.2 表 5 QPAS在算例2.2上的布局坐标 |
| Table 6 The detailed coordinates of the disks for instance 2.3 表 6 QPAS在算例2.3上的布局坐标 |
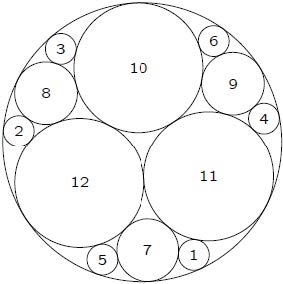
|
Fig. 4 Packing layout of instance 2.2 图 4 算例2.2 的布局图 |
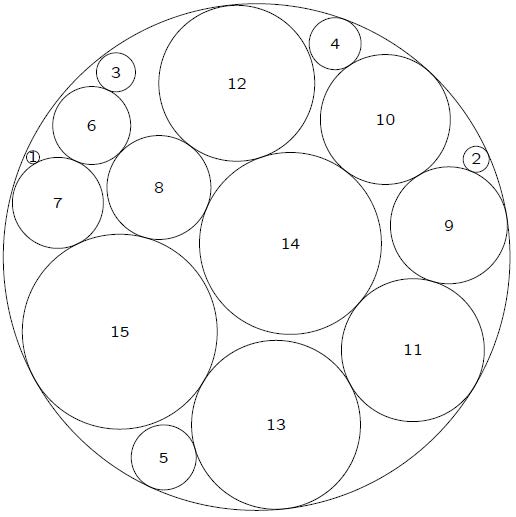
|
Fig. 5 Packing layout of instance 2.3 图 5 算例2.3 的布局图 |
由前两组算例的计算结果对比可见,对于静不平衡量,总的来说,QPAS与QPCFA的精度基本相当,比其他算法的精度普遍要高出1~7个数量级.对于计算的时间,MPSO和APSO取40次计算的平均时间,ISS取50次计算的平均时间,QPCFA取1次计算的时间,IQP、BF、HSA、TSH和QPAS取5次计算的平均时间.各算法的编程语言和运行的硬件环境如下:MASP在CPU主频为166 MHz的PC机上实验,编程语言和机器内存未见报道;APSO使用MATLAB语言编程实现,在CPU主频为2.0 GHz、内存为256 MB的PC机上进行计算;IQP和ISS使用C语言编程实现,在CPU主频为2.4 GHz、内存为512 MB的PC机上进行计算;HSA使用Java语言编程实现,在CPU主频为1.6 GHz、内存为512 MB的PC机上进行计算;BF和TSH使用Java语言编程实现,在CPU主频为1.6 GHz、内存为1 GB的笔记本上进行计算;QPCFA使用C++语言编程实现,在CPU主频为1.9 GHz、内存为1 GB的PC机上进行计算.虽然计算环境有所差异,但基本处于同一数量级.从两个表中可见,QPAS与其他几种算法的计算时间相当甚至略快.
对于第3组算例,表 7给出了QPAS与PA[5]和SATS[4]的计算结果的比较.在这3种算法中,QPAS的计算结果很接近于典型的圆形Packing问题的最好结果.由于带平衡约束的圆形Packing问题比典型的圆形Packing问题多了一项平衡约束,后者的最优解一定好于等于前者的最优解.因此QPAS计算结果略弱于典型圆形Packing问题的解是可以理解的.另外,QPAS在算例3.1找到了更小的外包络圆半径.QPAS在第3组算例取得的布局如图 6和图 7所示.
| Table 7 Computing results on the third set of instances 表 7 第3组算例计算结果比较 |

|
Fig. 6 Packing layout of instance 3.1 图 6 算例3.1 的布局图 |
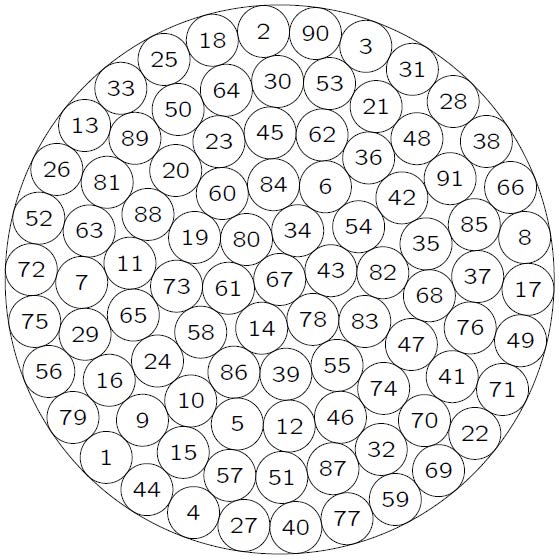
|
Fig. 7 Packing layout of instance 3.2 图 7 算例3.2 的布局图 |
5 结 论
对于带平衡约束的圆形Packing问题,基于弹力模型和拉力模型,把拟物下降方法与若干拟人策略相结合以提高连续优化的效率.当拟物过程遇到局部陷阱需要跳坑时,由于外包络圆中的剩余空间都是不规则的,很难通过精确计算从中选出最空闲的空间以作为跳坑的位置.本文通过化圆为方,将外包络圆和待置入圆饼近似看做矩形,并借鉴求解矩形Packing问题的拟人算法中动作空间的概念,把不规则的剩余空间转化为易计算和比较的矩形空间,从而较快且较准确地找到最空闲空间.对国际上公开的13个代表性算例的计算结果表明,所提的拟物求解算法是快速且有效的.在今后的工作中,拟进一步提高基于动作空间的跳坑方法的有效性,并将其应用到一般的圆形Packing问题的求解中去.
| [1] | Kang Y, Huang WQ. A fast quasi-physical algorithm for the disks packing problem. Computer Engineering and Applications, 2003, 39 (35) :30–32(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200335009.htm |
| [2] | Wang HQ, Huang WQ, Zhang Q, Xu DM. An improved algorithm for the packing of unequal circles within a larger containing circle. European Journal of Operational Research, 2002, 141 (2) :440–453. [doi:10.1016/S0377-2217(01)00241-7] http://cn.bing.com/academic/profile?id=2039006199&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | Liu JF, Zhou GC, Pan JJ. Heuristic algorithm based on Taboo search for sphere packing problem. Application Research of Computers, 2011, 28 (3) :892–894(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201103026.htm |
| [4] | Zhang D, Deng A. An effective hybrid algorithm for the problem of packing circles into a larger containing circle. Computers&Operations Research, 2005, 32 (8) :1941–1951. http://cn.bing.com/academic/profile?id=2054450094&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | Zhang DF, Li X. A personified annealing algorithm for circles packing problem. Acta Automatica Sinica, 2005, 31 (4) :590. http://cn.bing.com/academic/profile?id=2388237407&encoded=0&v=paper_preview&mkt=zh-cn |
| [6] | Theodoracatos VE, Grimsley JL. The optimal packing of arbitrarily-shaped polygons sing simulated annealing and polynomial-time cooling schedules. Computer&Methods in Applied Mechanics and Engineering, 1995, 125 (1) :53–70. |
| [7] | Graham RL, Lubachevsky BD, Nurmela KJ, Östergård PRJ. Dense packing of congruent circles in a circle. Discrete Mathematics, 1998, 181 (1) :139–154. http://cn.bing.com/academic/profile?id=2055789678&encoded=0&v=paper_preview&mkt=zh-cn |
| [8] | Yu Y, Cha JZ, Tang XJ. Learning based GA and application in packing. Chinese Journal of Computers, 2001, 24 (12) :1242–1249(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200112001.htm |
| [9] | Teng HF, Sun SL, Ge WH, Zhong WX. Layout optimization for the dishes installed on a rotating table-the packing problem with equilibrium behavioural constraints. SCIECE IN CHINA (Series A), 1994, 37 (10) :1272–1280. http://cn.bing.com/academic/profile?id=2351659130&encoded=0&v=paper_preview&mkt=zh-cn |
| [10] | Tang F, Teng HF. A modified genetic algorithm and its application to layout optimization. Ruan Jian Xue Bao/Journal of Software, 1999, 10 (10) :1096–1102(in Chinese with English abstract). [doi:10.13328/j.cnki.jos.1999.10.014] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=19991014&journal_id=jos |
| [11] | Qian ZQ, Teng HF, Sun ZG. Human-Computer interactive genetic algorithm and its application to constrained layout optimization. Chinese Chinese Journal of Computers, 2001, 24 (5) :553–559(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200105018.htm |
| [12] | Huang WQ, Chen M. Note on:An improved algorithm for the packing of unequal circles within a larger containing circle. Computers&Industrial Engineering, 2006, 50 (3) :338–344. http://cn.bing.com/academic/profile?id=2042072561&encoded=0&v=paper_preview&mkt=zh-cn |
| [13] | Li N, Liu F, Sun DB. A study on the particle swarm optimization with mutation operator constrained layout optimization. Chinese Journal of Computers, 2004, 27 (7) :897–903(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200407004.htm |
| [14] | Lei KY, Qiu YH. A study of constrained layout optimization using adaptive particle swarm optimizer. Journal of Computer Research and Development, 2006, 43 (10) :1724–1731(in Chinese with English abstract). [doi:10.1360/crad20061008] |
| [15] | Liu J, Huang WQ. A fast local search algorithm for solving circles packing problem with constraints of equilibrium. Journal of Image and Graphics, 2008, 13 (5) :991–997(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB200805025.htm |
| [16] | Wang YS, Shi YJ, Teng HF. An improved scatter search for circles packing problem with the equilibrium constraint. Chinese Journal of Computers, 2009, 32 (6) :1214–1221(in Chinese with English abstract). [doi:10.3724/SP.J.1016.2009.01214] |
| [18] | Liu JF, Li G, Chen DB, Liu WJ, Wang YL. Two-Dimensional equilibrium constraint layout ssing simulated annealing. Computers&Industrial Engineering, 2010, 59 (4) :530–536. http://cn.bing.com/academic/profile?id=184229581&encoded=0&v=paper_preview&mkt=zh-cn |
| [20] | He K, Mo DZ, Xu RC, Huang WQ. A quasi-physical algorithm based on coarse and fine adjustment for solving circles packing problem with constraints of equilibrium. Chinese Journal of Computers, 2013, 26 (6) :1224–1234(in Chinese with English abstract). http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201306010.htm |
| [21] | He K, Huang WQ. An efficient placement heuristic for three-dimensional rectangular packing. Computer&Operations Research, 2011, 38 (1) :227–233. http://cn.bing.com/academic/profile?id=2030163722&encoded=0&v=paper_preview&mkt=zh-cn |
| [23] | He K, Huang WQ, Jin Y. An efficient deterministic heuristic for two-dimensional rectangular packing. Computers&Operations Research, 2012, 39 (7) :1355–1363. http://cn.bing.com/academic/profile?id=2007771215&encoded=0&v=paper_preview&mkt=zh-cn |
| [24] | He K, Huang WQ, Jin Y. Efficient algorithm based on action space for solving the 2D rectangular packing problem. Ruan Jian Xue Bao/Journal of Software, 2012, 23 (5) :1037–1044(in Chinese with English abstract). [doi:10.3724/SP.J.1001.2012.03986] |
| [1] | 康雁, 黄文奇. 求解圆形Packing问题的一个快速拟物算法. 计算机工程与应用, 2003,39 (35) :30–32. http://www.cnki.com.cn/Article/CJFDTOTAL-JSGG200335009.htm |
| [3] | 刘景发, 周国城, 潘锦基. 基于禁忌搜索的启发式算法求解球体Packing问题. 计算机应用研究, 2011,28 (3) :892–894. http://www.cnki.com.cn/Article/CJFDTOTAL-JSYJ201103026.htm |
| [8] | 于洋, 查建中, 唐晓君. 基于学习的遗传算法及其在布局中的应用. 计算机学报, 2001,24 (12) :1242–1249. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200112001.htm |
| [10] | 唐飞, 滕弘飞. 一种改进的遗传算法及其在布局优化中的应用. 软件学报, 1999,10 (10) :1096–1102. [doi:10.13328/j.cnki.jos.1999.10.014] http://www.jos.org.cn/ch/reader/view_abstract.aspx?flag=1&file_no=19991014&journal_id=jos |
| [11] | 钱志勤, 滕弘飞, 孙治国. 人机交互的遗传算法及其在约束布局优化中的应用. 计算机学报, 2001,24 (5) :553–559. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200105018.htm |
| [13] | 李宁, 刘飞, 孙德宝. 基于带变异算子粒子群优化算法的约束布局优化研究. 计算机学报, 2004,27 (7) :897–903. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200407004.htm |
| [14] | 雷开友, 邱玉辉. 基于自适应粒子群优化算法的约束布局优化研究. 计算机研究与发展, 2006,43 (10) :1724–1731. [doi:10.1360/crad20061008] |
| [15] | 刘建, 黄文奇. 求解带平衡约束圆形Packing问题的快速局部搜索算法. 中国图像图形学报, 2008,13 (5) :991–997. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB200805025.htm |
| [16] | 王奕首, 史彦军, 滕弘飞. 用改进的散射搜索法求解带平衡约束的圆Packing问题. 计算机学报, 2009,32 (6) :1214–1221. [doi:10.3724/SP.J.1016.2009.01214] |
| [17] | 刘景发, 李刚. 求解带平衡性能约束的圆形装填问题的吸引盘填充算法. 中国科学:信息科学, 2010,40 (3) :423–432. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201003006.htm |
| [19] | 李刚, 刘景发. 基于禁忌搜索的启发式算法求解带平衡约束的圆形装填问题. 中国科学:信息科学, 2011,41 (9) :1076–1088. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201109005.htm |
| [20] | 何琨, 莫旦增, 许如初, 黄文奇. 基于粗精调技术的求解带平衡约束圆形Packing问题的拟物算法. 计算机学报, 2013,26 (6) :1224–1234. http://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201306010.htm |
| [22] | 何琨, 黄文奇. 三维矩形Packing问题的拟人求解算法. 中国科学:信息科学, 2010,40 (12) :1586–1595. http://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201012004.htm |
| [24] | 何琨, 黄文奇, 金燕. 基于动作空间的求解二维矩形Packing问题的高效启发式算法. 软件学报, 2012,23 (5) :1037–1044. [doi:10.3724/SP.J.1001.2012.03986] |
 2016, Vol. 27
2016, Vol. 27


