当今, 社会信息化和网络化的发展导致数据呈爆炸式增长.大数据的涌现, 使人们处理计算问题时获得了前所未有的大规模样本, 但同时也不得不面对更加复杂的大数据处理:数据复杂且规模巨大^[1-3].在现实的诸多应用中, 数据的表现形式存在着诸多不确定性, 比如说, 数据的缺失、收集不准确、数据集粒度过于粗糙等都会导致不确定性数据的产生.在此背景下, 模糊集、粗糙集等处理不确定性数据的理论和方法应运而生, 并成为处理不确定性数据的有效工具^{[4, 5]}.

粗糙集(rough set)首先由Pawlak提出, 它主要是研究由不可分辨引起的不确定信息的智能处理的理论.目前, 粗糙集理论已成为一种重要的不确定信息处理技术^{[6, 7]}, 该理论已经在机器学习和知识发现、数据挖掘、决策支持与分析等方面得到广泛应用^[8].

模糊粗糙集理论中, 作为模糊集与粗糙集的融合理论, 兼顾数据的模糊性与不可分辩性^[9-14].模糊粗糙集利用模糊粗糙近似算子将被隐藏在不确定数据中的信息, 按照确定的规则呈现出来.模糊粗糙集可以更好地处理数据中的不确定性, 但是该理论不能处理大规模数据.这是由于模糊粗糙集所依赖的理论核心——模糊粗糙近似算子的复杂度, 是元素个数的平方量级^{[9, 15, 16]}.无法解决这个问题, 粗糙集的研究就无法应用到大数据的背景当中去.因此, 在本文中, 我们将就这个问题进行研究, 希望能够通过某种方式, 降低其复杂度, 使不确定性研究能够恰当地应用到大数据中去.

本文将随机抽样引入了传统的模糊粗糙集中, 对近似逼近算子的效率进行了大幅提升.本文的主要内容为:巧妙地引入随机抽样, 构建统计粗糙集模型.首先, 我们通过引入随机抽样提出了一个限定区域k-limit的概念, 限定区域可以极大地缩小下近似的计算规模.然后, 基于k-limit我们又提出统计上、下近似概念.并且, 在引入随机抽样的同时, 用充分完备的定理和证明, 验证了新概念和理论的可靠性, 从而构建出统计粗糙集模型.

1 模糊粗糙集及约简 1.1 模糊粗糙集模型

假设全集U是一个有着有限个数元素的非空集合, 记做$U=\{ {x_1}, {x_2}, ..., {x_n}\}.$每一个元素都有着一系列条件属性, 记做$R=\{ {r_1}, {r_2}, ..., {r_m}\}; $以及决策属性D.于是(U, (R∪D))被称作是一个决策系统DS.

对于每一个P⊆R, 我们将二维关系P(x, y)称为P的模糊相似关系, 对于任意x, y, z∈U, 一个模糊相似关系满足自反性:P(x, x)=1;对称性:P(x, y)=P(y, x), 以及T-传递性:P(x, y)≥T(P(x, z), P(z, y)).简单来说, P是用来代表其相似关系的, F(·)用来代表模糊幂集.

模糊粗糙集是用来将模糊集和粗糙集结合起来的工具.它在文献[1]中首次被Dubois和Prade提出.然后其细节在文献[10, 15, 16]中被深入地加以研究.总体上来说, 如今的模糊粗糙集可以被下列4个近似算子概括.

$ \underline {{R_\vartheta }} A(x)={\inf _{u \in U}}\vartheta (R(u, x), A(u)), \overline {{R_T}} A(x)={\sup _{u \in U}}T(R(u, x), A(u)), \\ \underline {{R_S}} A(x)={\inf _{u \in U}}S(N(R(u, x)), A(u)), \overline {{R_\sigma }} A(x)={\sup _{u \in U}}\sigma (N(R(u, x)), A(u)). $

在文献[9, 10]中介绍了经典模糊粗糙集的下近似, 实际上是该样本到不同类别样本之间的最小距离, 而上近似则是到相同类别样本之间的最大相似度.模糊粗糙集的上、下近似的几何意义有助于我们设计基于随机抽样的统计粗糙集.

1.2 常见约简算法的实验比较分析

常见的属性约简方法主要有两种:一种是基于依赖度函数的方法, 另一种是基于辨识矩阵的方法.详细的算法比较请参考文献[15].

本实验中所使用的测试环境如下:

(1) 硬件:Intel(R) Xeon(R) CPU ES-2670, 2.6GHz;

(2) 内存:252GB;

(3) 编程语言:C++;

(4) 操作系统:Linux.

实验中使用的数据库均从UCI选出.这些数据集的详细信息在表 1中给出.在实验中使用了10-交叉验证.

本节我们将从时间复杂度和空间复杂度上对比辨识矩阵算法和依赖度算法的可扩展性.在给出计算复杂度的比较之后, 再给出具体的实验比较.

基于依赖度的约简算法的时间复杂度为O(|U|²×|R|³), 空间复杂度为O(|U|²×|R|).基于辨识矩阵的约简算法的时间复杂度为O(|U|²×|R|²), 空间复杂度为O(|U|²×|R|).由此可以看出, 两种算法的空间复杂度相当, 但是基于辨识矩阵的算法时间复杂度要明显小于基于依赖度的约简算法的时间复杂度.下面的实验比较说明了这一点.

(1) 运行时间的对比

表 2显示了两种约简算法的运行时间.表 2说明, 依赖度函数的运行时间消耗要远大于辨识矩阵, 特别是当数据集记录数增大, 或者是属性数增多的时候.

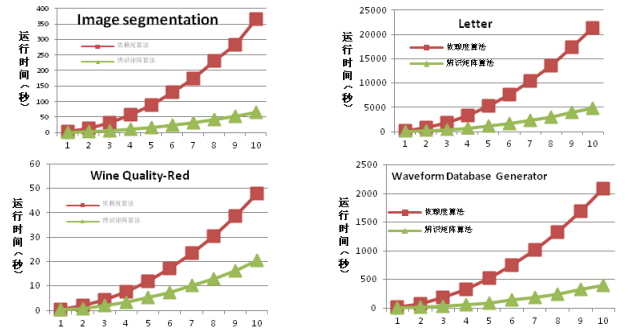
为了更加清晰地比较两种算法的运行时间, 我们用递增的数据集来比较两种算法.具体情况如图 1所示, 其中, 横轴从1~10, 是将数据集均匀分成了1~10份, 取其中的一份进行实验, 逐渐增大, 直到取10份进行实验, 此时就是全部数据集.

在图 1中, 我们可以清晰地看到, 随着数据集的增大, 基于依赖度函数的算法运行时间急剧增大, 而辨识矩阵算法增加得则相对较慢.从这些图中我们可以看出, 在大规模数据集上, 辨识矩阵算法比依赖度算法更有优势.

(2) 运行空间的对比

表 3比较了两种约简算法运行空间消耗的情况.两种算法在较大规模数据集上都有着很高的空间消耗.

由于依赖度的属性约简算法通常有着高空间和高时间复杂度, 而虽然基于辨识矩阵的约简算法提升了时间方面的效率, 但是由于空间消耗过大, 仍然无法应用到大规模数据集上.因此, 为了能够将属性约简应用到大规模数据集上, 新方法的提出便势在必行.

2 统计粗糙集模型

对于∀x∈U, 下近似值就是到不同类别点的最小距离.假设y恰好就是x取到异类点(与x所属的类别不同的点)最小值的记录.很明显, x和y必然有某些维度上非常接近.因为, 如果x和y在所有维度上都距离很远, 那么x就不会在y上取到异类点的最小距离.基于这个逻辑, 将整个数据库在该维度(属性)上排序, 那么x和y一定会离得比较接近.于是我们提出两个概念, k-neighbor和k-limit, 用来定义某元组的邻居.

定义2.1(k-neighbor). 给出一个随机变量X和它的n个样本升序排列:$\{ {x_1}, {x_2}, ..., {x_n}\}, $那么x_i的k-neighbor可以表达成:

$ \left\{ \begin{array}{l} {x_1}, ..., {x_i}, ..., {x_{i + k}}, {\rm{ if }}i-k < 1\\ {x_{i-k}}, ..., {x_i}, ..., {x_n}, {\rm{ if }}i + k > n\\ {\rm{ }}{x_{i-k}}, ..., {x_i}, ..., {x_{i + k}}, {\rm{ others}} \end{array} \right., {\rm{ }}1 \le k \le \arg (n/2). $

定义2.2(k-limit). 给出一个决策表DT=(U, R, D), 其中, $U=\{ {x_1}, {x_2}, ..., {x_n}\}, R=\{ {r_1}, {r_2}, ..., {r_m}\}.$对于所有属性, 1≤k≤arg(n/2)将x_i在每一个属性上的k-neighbor集中到一个集合中.这个集合就叫作x_i的k-limit(限定区域).这里的k, 就是限定长度.

基于k-limit, 我们可以定义一对新的上、下近似算子.

定义2.3. 给出一个决策表DT=(U, R, D), 其中, $U=\{ {x_1}, {x_2}, ..., {x_n}\}, R=\{ {r_1}, {r_2}, ..., {r_m}\}, $F(U)是U的模糊幂函数集合.对于∀;x∈U, A∈F(U), x的k-统计下近似算子和k-统计上近似算子可以如下表示:

$ \begin{array}{l} \underline {R_\vartheta ^k} A(x)={\inf _{u \in k{\rm{-}}\lim it(x)}}\vartheta (R(u, x), A(u)), \overline {R_T^k} A(x)={\sup _{u \in k{\rm{-}}\lim it(x)}}T(R(u, x), A(u)), \\ \underline {R_S^k} A(x)={\inf _{u \in k{\rm{-}}\lim it(x)}}S(N(R(u, x)), A(u)), \overline {R_\sigma ^k} A(x)={\sup _{u \in k{\rm{-}}\lim it(x)}}\sigma (N(R(u, x)), A(u)). \end{array} $

性质2.1.

(1) K-统计下近似算子不小于经典的下近似算子;

(2) K-统计上近似算子不大于经典的下近似算子.

证明:对于∀;x∈U, $k \le {\mathop{\rm int}} (n/2) \Rightarrow k{\rm{ - }}\lim it(x) \subseteq U \Rightarrow $

$ \begin{array}{l} \underline {R_\vartheta ^k} A(x)={\inf _{u \in k{\rm{-}}\lim it(x)}}\vartheta (R(u, x), A(u)) \ge {\inf _{u \in U}}\vartheta (R(u, x), A(u))=\underline {{R_\vartheta }} A(x); \\ \overline {R_T^k} A(x)={\sup _{u \in k{\rm{-}}\lim it(x)}}T(R(u, x), A(u)) \le {\sup _{u \in U}}T(R(u, x), A(u))=\overline {{R_T}} A(x); \\ \underline {R_S^k} A(x)={\inf _{u \in k-\lim it(x)}}S(N(R(u, x)), A(u)) \ge {\inf _{u \in U}}S(N(R(u, x)), A(u))=\underline {{R_S}} A(x); \end{array} $

性质2.2. 当k→int(n/2)时, k-统计近似算子的极限也趋向于经典的近似算子.

定义2.3提供了一种新的方法, 用更少的计算量来拟合经典的近似算子.性质2.1和性质2.2展示出, 在k足够大时, k-统计近似算子可以逼近经典的近似算子.但是如何最小化限定距离k是一个问题.考虑到随机抽样可以做到在统计上无偏估计经典上、下近似值, 并可极大地缩小计算量.基于随机抽样, 可确定限定距离k的大小.

定义2.4. 对于$A=\left\{ {{\lambda _1}, {\lambda _2}, ..., {\lambda _n}} \right\}, A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}, $其中, ${\lambda _i}, {\lambda '_i} \in [0, 1], \forall i=1, 2, ..., n.$如果

$ \left| {{\lambda _i}-{{\lambda '}_i}} \right| \le \delta (0 \le \delta \le 1), $

我们就说$({\lambda _i}, {\lambda '_i})$是一个δ-近似对.

定义2.5. 对于$A=\left\{ {{\lambda _1}, {\lambda _2}, ..., {\lambda _n}} \right\}, A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}, $其中, ${\lambda _i}, {\lambda '_i} \in [0, 1], \forall i=1, 2, ..., n.$如果集合A和A'中δ-近似对的数量是p对, 那么我们称p/n是A和A'之间的相似度, 记做$p={\gamma _{A \approx A'}}.$

用样本比例p作为总体的比例估计P, 则p是P的无偏估计.下面的性质说明了这一点.同时, 我们还给出了p和P的方差的统计性质.

性质2.3. 对于简单随机抽样, E(P)=E(p)=P.

证明略, 详细论证请见文献[17]第30页定理2.1及其推论2.2.

性质2.4. 对于简单随机抽样, p的方差为$V(p)=\frac{{PQ}}{a}\frac{{(n-a)}}{{(n-1)}}, Q=1-P, $并且$V(p)=\frac{{PQ}}{a}\frac{{(n-a)}}{{(n-1)}}, Q=1-P$是V(P)的无偏估计.

证明略, 详细论证请见文献[17]第31页定理2.2及其推论2.5、推论2.8.

在p和P具有以上统计性质时, 以及在用样本比例p估计总体比例P时, 样本容量a的确定方法可以如下设计.

定理2.1.给出一个决策表DT=(U, R, D), 其中, $U=\{ {x_1}, {x_2}, ..., {x_n}\}.S=\{ {s_1}, {s_2}, ..., {s_a}$是随机地从全集U中抽样得出的样本集.当$a > \frac{{{t^2}p(1-p)}}{{{d^2}}}$时, 满足以下条件, 则至少以e的置信度, 使得$P=p \pm d\%.$

(1) $P={\gamma _{A \approx A'}}, $其中, $A=\left\{ {{\lambda _1}, {\lambda _2}, ..., {\lambda _n}} \right\}$是$\{ {x_1}, {x_2}, ..., {x_n}\} $的下近似值.$A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}$是$\{ {x_1}, {x_2}, ..., {x_n}\} $的k-统计下近似.

(2) $p={\gamma _{B \approx B'}}, $其中, $B=\left\{ {{\beta _1}, {\beta _2}, ..., {\beta _n}} \right\}$是$\{ {s_1}, {s_2}, ..., {s_a}\} $的下近似值.$B'=\left\{ {{{\beta '}_1}, {{\beta '}_2}, ..., {{\beta '}_n}} \right\}$是$\{ {s_1}, {s_2}, ..., {s_a}\} $的k-统计下近似.

(3) t是标准正态分布的1-e双侧分位数.

证明:在简单随机抽样中, 可以用样本比例p作为总体比例估计P.由于E(P)=E(p)=P, 故而p是P的无偏估计.由于p的方差为$V(p)=\frac{{PQ}}{a}\frac{{(n-a)}}{{(n-1)}}, Q=1-P; $绝对误差限度为$d=t\sqrt {V(\tilde \theta)}; $上两式合并可得:

$ d=t\sqrt {V(\tilde \theta)}=t\sqrt {\frac{{PQ}}{n}\frac{{N-n}}{{N-1}}}. $

经过化简可得:

$ a=\frac{{{t^2}\frac{{PQ}}{{{d^2}}}}}{{1 + \frac{1}{n}\left({{t^2}\frac{{PQ}}{{{d^2}}}-1} \right)}}. $

由于1≤n, $\frac{1}{n} \to 0, $因此, $a > \frac{{{t^2}PQ}}{{{d^2}}}.$

由上述定理可以看出, 样本容量的确定与绝对误差限度d成反比, 与分布双侧分位数t和置信度(1-α)成正比.即要求的精度越高, 所需的样本容量越大.也就是说, 该定理保证了用抽样集合计算出的限制距离k以很高的置信度和很小的误差近似等于真实的、由全集U计算出的限制距离.

同时, 在保证置信度α确定的前提下, 该定理给出了样本容量的下限.也就是说, 通过随机抽样, 可以采用相对小的样本集, 快速确定限制距离k.

3 基于统计粗糙集模型的下近似算法设计

在统计粗糙集模型中, 为了计算统计下近似, 我们必须先得到限定距离k, 然后确定k-limit的范围.下面的一种算法即用来计算限定距离k.

3.1 计算限定距离k的算法设计

一个很朴素的解决方案是, 首先对k赋一个较小的初值, 然后尝试使用此k值下的k-limit计算统计下近似值, 然后与真实下近似进行对比, 如果有一定比例(达到阈值)的统计下近似值和真实下近似值相同(或者在可控误差范围内), 那么, 就认为这个限定距离是合适的.我们引入随机抽样, 从而不需要计算全部的真实下近似, 而只需要计算样本集中的真实下近似即可.

算法3.1. 计算限定距离k.

输入:DT=(U, R, D), $U=\{ {x_1}, {x_2}, ..., {x_n}\}, R=\{ {r_1}, {r_2}, ..., {r_m}\}, $d, e;

输出:限定距离k.

第1步.计算$a={\max _p}\left({\frac{{{t^2}p(1-p)}}{{{d^2}}}} \right), $然后随机从全集U中抽取样本集$S=\{ {s_1}, {s_2}, ..., {s_a}\}; $

第2步.计算S中所有样本的真实下近似, ${\lambda _i}=\underline {R_\vartheta ^{}} {[{s_i}]_D}({s_i}), \forall i \in \{ 1, 2, ..., a\}; $令$A=\left\{ {{\lambda _1}, {\lambda _2}, ..., {\lambda _n}} \right\}; $

第3步.k←1, 对于$\forall i \in \{ 1, 2, ..., a\}, $计算s_i的k-limit;

第4步.对于$\forall i \in \{ 1, 2, ..., a\}, $计算${\lambda '_i}=\underline {R_\vartheta ^1} {[{s_i}]_D}({s_i}), $令$A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}; $

第5步.计算$p={\gamma _{A \approx A'}}; $

第6步.while p < 1, do:

    (6.1)  k←k×2;

    (6.2) 对于$\forall i \in \{ 1, 2, ..., a\}, $计算s_i的k-limit;

    (6.3) 对于$\forall i \in \{ 1, 2, ..., a\}, $计算${\lambda '_i}=\underline {R_\vartheta ^1} {[{s_i}]_D}({s_i}), $令$A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}; $

    (6.4) 计算$p={\gamma _{A \approx A'}}; $

第7步.输出限定距离k.

在算法3.1中, 我们使用随机抽样去验证此时的限定距离k是否已经足够得到准确的统计下近似值.定理2.1则保证了, 用样本集得到的限定距离k, 与全集中得到的k统计误差极小.

得到限定长度之后, 下面我们将利用它来计算统计下近似.

3.2 计算统计下近似算法设计

根据上面得到的限定距离k, 我们将设计一种算法来计算统计下近似值.

算法3.2. 计算统计下近似值.

输入:DT=(U, R, D), $U=\{ {x_1}, {x_2}, ..., {x_n}\}, R=\{ {r_1}, {r_2}, ..., {r_m}\}, $限定距离k;

输出:所有元素的k-统计下近似值.

第1步.i←1;

第2步.while i≤n, do

    (2.1) 计算x_i的限定区域k-limit

    (2.2) 计算${\lambda '_i}=\underline {R_\vartheta ^k} {[{x_i}]_D}({x_i})$

    (2.3)  i←i+1

第3步.输出$A'=\left\{ {{{\lambda '}_1}, {{\lambda '}_2}, ..., {{\lambda '}_n}} \right\}.$

4 实验

本文实验均是在Linux下, 由C++编码完成.实验所使用的硬件参数是:CPU为Intel Xeon CPU ES-2670 2.6GHz, 内存为252GB.

本文实验将应用6个UCI数据集^[18], 用来验证统计下近似算法的效率.具体数据集参数见表 4.在具体实施随机抽样时, 考虑到数据分布的特征, 我们采用的是分层随机抽样法.根据不同类别记录的比值, 按比例分配每一类随机抽样的个数.此时, 不同类别随机抽样个数的总数仍是根据定理2.1计算出的样本量的数值.

4.1 统计下近似的运行时间

表 5代表了统计下近似和真实下近似的算法的时间消耗.由表 5我们可以看出, 真实算法和统计算法对于6个数据集进行下近似的时间消耗, 这体现了随机抽样算法在机选(统计)下近似时的高效率.

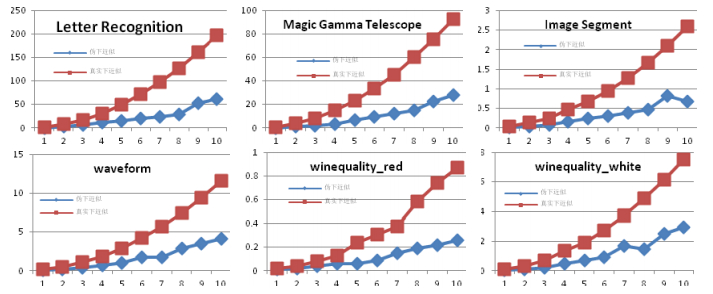
为了更好地展示计算的时间和空间, 我们把这6个数据集分割成10个等分.第1部分被看成是1st data set, 第2部分被看成是2nd data set, …, 第10部分被看成是10th data set.我们将用这些被分割过的数据集来观察所提出的统计下近似的算法和真实下近似的算法在数据集不断增大时的表现.图 2中, 清晰地展示了随着数据集的增大两种算法的下近似时间消耗情况.

从表 5和图 2我们可以清晰地看出, 随着数据集的增大, 下近似的计算时间也在逐步增大.我们可以从图中看出, 基于随机抽样的算法, 相对于真实下近似算法, 时间消耗明显较少.这是由于, 通过随机抽样以及限定区域k来计算统计下近似.此外, 基于随机抽样的算法随着数据集的增大, 它的时间消耗增大并不明显.而真实下近似的计算时间随数据集的增大, 其时间消耗急速增加.这体现出了基于随机抽样统计下近似的优越性——数据集越大, 其时间优势越明显.

在统计粗糙集模型中, 我们针对下近似的计算, 通过限定区域k-limit和随机抽样进行了优化, 使之成为统计下近似, 在保证其精度的情况下, 大幅度缩减了计算(统计)下近似的时间消耗.验证了在计算下近似时间效率方面, 随机抽样算法的优越性.并且, 可以看到, 数据集越大, 随机抽样算法在计算下近似的时间消耗方面其优势越显著.

综上, 我们可以得出结论, 随机抽样算法在下近似时间效率方面, 相比传统的下近似算法都有着大幅提升, 并且这种提升随着数据集的增大会更加显著.因此, 随机抽样算法确实弥补了传统下近似方法无法应用到大规模数据集上的不足.而且, 随机抽样算法的可扩展性较强, 可适用于大规模数据集.

4.2 统计下近似的效果比较

在本小节, 我们的目的是展示统计下近似的知识发现的效果.我们从以下两个方面展示统计下近似的知识发现的效果:一方面是基于统计下近似的约简的运行时间, 另一方面是基于统计下近似的约简的精度.

下面, 我们将观察约简时间随数据集大小变化的情况.

在表 6中我们可以清晰地发现, 依赖度算法和辨识矩阵算法空间消耗大致相同, 在一个数量级上.而随机抽样算法的空间消耗相对于另外两种来说非常之小, 所降低的空间消耗量级约在2个数量级到3个数量级之间.这体现了随机抽样算法在进行属性约简时的优越性, 特别是在大规模数据集下体现出的优越性.

表 7和表 8列出了3种约简方法所得约简结果的分类精度, 可以看到所有属性的分类精度最佳, 而经典的两种方法——辨识矩阵约简方法和依赖度约简方法的约简结果的分类精度相近.基于统计抽样的约简方法在不同的抽样情况下所得到的约简的分类精度不同, 但却相近.而且它们均略微低于经典的两种约简方法的精度.

综上, 我们可以得出结论, 随机抽样算法虽然在某些时候会对约简精度有小幅度但可控的下降, 但其在下近似时间效率、属性约简时间效率方面, 相比传统的属性约简算法都有着大幅提升, 并且这种提升随着数据集的增大会更加显著.因此, 随机抽样算法确实改善了传统属性约简方法无法应用到大规模数据集上的缺陷.

5 结论与展望

本文将随机抽样引入到经典的模糊粗糙集理论中, 建立了统计粗糙集模型, 设计了计算统计下近似的算法.本文的创新点在于:将随机抽样和经典的模糊粗糙集相结合, 将随机抽样代入到模糊粗糙集的基本理论中, 提出了限制区域k-limit(x)的概念, 将计算范围限制到更小、更有效的范围, 提出了统计上、下近似等概念, 构建了统计粗糙集模型.