2. Simula Research Laboratory & University of Oslo, Oslo 1325, Norway
2. Simula Research Laboratory & University of Oslo, Oslo 1325, Norway
信息物理系统作为计算进程和物理进程的统一体,是集成计算、通信与控制于一体的新一代智能系统[1].信息物理系统已经逐步应用于各个领域,如航空、能源、医疗等.由于信息物理系统的复杂性、异构性和多样性,实际开发中多采用产品线工程的方式,以提高产品的质量和开发效率.产品线工程的目标是:通过对核心资产的重用,以更快、更安全、更廉价的方式进行相似产品的开发[2].产品线工程通常包含两个阶段:第1个阶段为领域工程阶段,主要是构建核心可重用可配置的资产;第2个阶段为应用工程阶段,通过对核心资产的配置,以生成特定的产品.基于模型驱动的产品线工程是通过将核心资产抽象为模型,以模型的构建、验证和分析以及配置和转换等来驱动产品的开发.基于模型驱动的产品线工程可以降低开发成本,提高开发质量和效率.
在基于模型驱动的产品线配置中,配置数据需要满足一系列预定义的约束(conformance constraints,也称为一致性或符合性约束)以保证配置数据的有效性,即,要保证配置数据的符合性或一致性(后文统一称为一致性).由于人工配置难免会导致配置数据的不一致,而人工修复很难且效率低下,因此需要一种高效的不一致修复方法以保证配置的效率.在最近发布的一项调查研究中[3],两组配置用户(Linux-97人,eCos-9人)都认为,错误修复是其在配置系统时的一个主要挑战.而信息物理系统产品线体系结构模型的配置修复尤其复杂,主要由于以下两个方面的原因:(1) 在信息物理系统产品线体系结构模型中通常存在数量巨大的可变点、可变点实例以及它们之间复杂的约束,在修复一处不一致的时候很难保证不引入新的不一致;(2) 对于不一致的修复可能会存在成百上千种修复方案,而不同的修复方案对于整个配置效率的影响是不同的,如果没有有效的方法给予支持,用户很难判断哪种修复方案对于整个配置过程的配置效率来说是最优的选择.而在当前的工业实践中,配置修复通常很大程度地依赖于领域专家自身的经验和知识,而且修复的效率低下,因此亟需一种有效的自动化手段来辅助配置人员完成配置.
Henard等人[4]在ICSE 2015上首次将多目标搜索和约束求解相结合,来进行基于特征模型的产品线配置.他们通过约束求解器来产生可行解,并改进IBEA(indicator-based evolutionary algorithm)算法[5],从可行解中寻找最优解,即,最优的特征选择方案.但是值得指出的是:虽然特征模型已被广泛应用于产品线工程中,却往往是在抽象层次较高的需求层描述产品线.而本文所面向的是信息物理系统产品线体系结构层,且相较于特征模型中的简单约束(强制或可选,需要或排斥),信息物理系统产品线体系结构层模型具有更复杂的约束关系.本文选用SimPL[6]描述系统产品线的共性和可变性,并采用OCL(object constraint language)[7]描述可变点之间的约束.为了将不一致性修复问题转化为带约束的多目标搜索问题进行求解,本文作者前期提出一种结合多目标搜索和约束求解的不一致修复推荐框架(Zen-Fix).为了提高Zen-Fix的搜索效率,增强其实用性,需要设计高效的搜索算法.虽然IBEA算法[5]已在产品线配置中得到成功应用[4,8],该算法有良好的收敛性,但在保持解的多样性方面表现较差.而差分进化算法[9]是目前最优秀的算法之一,已被广泛应用于各类全局优化问题.因此,IBEA算法与差分进化算法的结合具有很好的前景.
针对以上问题,本文针对基于多目标搜索的配置修复推荐框架Zen-Fix,提出一种新颖的DeIBEA算法,其主要贡献可以归纳为:
(1) 通过引入可行解与不可行解差分到IBEA算法,提高了IBEA算法在处理配置修复问题时的效率和搜索性能;
(2) 基于工业案例海底油田采控系统产品线中10 189个配置不一致问题,对Zen-Fix以及DeIBEA算法进行了验证.
1 研究背景在模型驱动的产品线工程中,产品线模型描述了整个产品家族所有产品的共性以及可变性.可变点标识了可变性发生的位置,可以通过值域、枚举,或者约束来定义;而可变体定义了该可变点相关的可变性实现的不同配置.需要指出的是:可变点只是可变性的一种抽象表达,在产品线配置过程中,可变点并不能直接被配置,只有实例化为可变点实例之后才可以被配置.
为了实现信息物理系统产品线体系结构模型的配置修复,第1.1节首先介绍了本文采用的建模语言;随后介绍了Zen-Fix运行的上下文,即所采用的交互配置过程(第1.2节);随后给出了前期针对OCL进行局部验证的工作(第1.3节);最后,大体介绍了Zen-Fix框架(第1.4节).
1.1 SimPL建模语言SimPL[6]语言是Simula研究院于2013年提出的一种面向信息物理系统产品线体系结构层的建模语言,它对UML(unified modeling language[10])进行扩展以支持可变性建模,且可以通过OCL描述可变点之间的复杂约束.SimPL支持4种类型的可变性,即基数可变性、类型可变性、属性可变性以及拓扑可变性.基数可变性描述了在产品模型中某一(些)可变点实例的个数,类型可变性表示产品中某一个类的具体子类型,属性可变性对应于类中可配置的属性,拓扑可变性描述了产品模型中实例的拓扑结构.拓扑可变性可以看作基数可变性和类型可变性的组合,对拓扑可变性的配置是从一系列预定义好的拓扑结构中进行选择.构造型 $\left\langle {} \right.$ ConfigurationUnit $\left. {} \right\rangle $ 应用于UML的包来结构化组织所有的可变点,并可以追踪至系统设计层的类,包的模板参数用来描述可变点.
如图 1所示是由SimPL描述的海底采油系统产品线的模型片段.一个海底采油系统的控制模块可以有多个海底电子模块(SEM),该可变性由基数可变点sEM描述,而电子模块控制的阀门可以有不同的类型,例如,注射阻塞阀门(InjectionChokeValve)即为其中一种类型,该可变性由类型可变点Valve描述.不同的海底采油系统可以设置容错参数(由属性可变性faultTolerant表示).
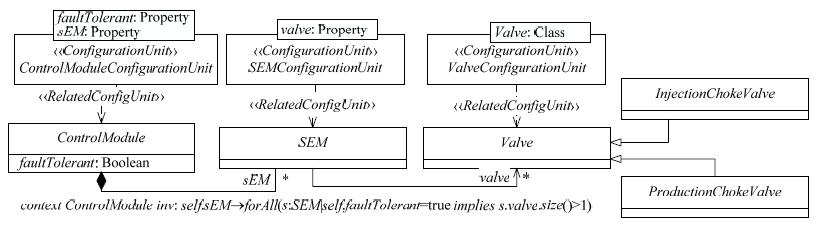
|
Fig. 1 Running example using SimPL methodology 图 1 SimPL模型实例片段 |
本文选用SimpL语言的原因主要是:(1) SimPL语言能够很好地满足信息物理系统产品线体系结构模型的建模需求,比如多视图支持软硬件建模以及软硬件部署关系的建模,支持对可变点的结构化建模以及与体系结构模型的追踪关系;(2) SimPL语言基于标准的UML扩展,具有较好的建模工具支持,简单、易用;(3) OCL作为UML的标准约束语言,可以用来描述信息物理系统产品线模型中复杂的约束关系,而这种约束关系是配置自动化的核心基础.
1.2 信息物理系统产品线的交互配置过程在信息物理系统产品线体系结构模型的配置过程中,由于存在大量的可变点、可变点实例以及其间的复杂约束关系,很难实现完全自动的产品配置.产品配置是一个易错且耗时的过程,因此需要一个半自动化的配置指导来支持产品配置,交互式产品线配置已经成为热点[11].而在交互式产品线配置过程中,用户的人工输入会不可避免地引入错误,为了保证产品配置的质量,需要工具自动化的配置支持,例如自动检查与修复.此外,由于交互式配置本身的特点,为检查和修复带来了很高的性能需求,其时间性能优劣是其能否在交互配置过程中进行成功应用的关键.我们的前期工作中提出一种增量一致性检查方法Zen-CC[12],以支持产品线交互配置.当配置人员配置完一个可变点实例,Zen-CC会局部更新由OCL约束集构成的验证森林,以增量检查当前配置是否符合相关约束,通过局部验证以达到较高的效率,实时地为配置人员反馈配置结果,以保证产品配置的质量.对于符合约束的配置,会触发配置推理功能对未配置的可变点实例进行自动配置.然而对于违背约束的配置,由于人工修复的困难性,则需要提供高效的自动化修复,也就是本文Zen-Fix的工作内容.对于不一致的配置,Zen-Fix可以实时地向配置用户推荐满足约束的最优解,用户从推荐的多个解中选择一个进行修复.此过程不断重复,直到配置完成所有的可变点实例.
1.3 增量OCL验证在交互式产品线配置过程中,需要实时地反馈给配置人员当前配置的有效性.有效的配置是指满足预定义约束集的配置,即,需要保证配置数据的一致性.为了保证验证的效率,在前期工作中提出一种通过局部验证与当前配置数据相关的OCL子约束来实现增量OCL验证的方法——Zen-CC.Zen-CC的核心是将每一个OCL约束都转换为一棵动态验证树,动态验证树包含4种类型的节点,即:根节点、迭代节点、逻辑节点以及叶子节点.此外,还定义了节点域表示验证树中每个节点所对应的可变点及实例.如图 2所示,是本文OCL实例(如图 1所示)的初始验证树.根节点表示树的根,根节点的域是相应OCL约束的上下文(context).迭代节点表示OCL中的迭代操作,如forAll,exists等,迭代节点的域为与其相关的基数可变点(图 2中可变点sEM).逻辑节点代表了OCL中的逻辑操作,比如and,or等,逻辑节点的域为空.叶子节点代表OCL中一个原子命题逻辑(原子布尔表达式),叶子节点的域表示原子命题逻辑中所直接约束的可变点(如图 2中属性可变性faultTolerant和基数可变性valve),该表达式的验证结果可以为true,false或者undefined.

|
Fig. 2 Initial validation tree for the OCL constraint of running example 图 2 模型实例中OCL的初始验证树 |
根据当前配置的可变点实例的类型不同,验证树有以下几种动态更新操作:
1) 分枝;
2) 剪枝:在构建初始的验证树时,所有的根节点和迭代节点的分支数目由该节点所对应的基数可变性的下界决定(本例中下界为1).当配置基数可变性时,根节点和迭代节点的分支数目需要根据配置数据进行相应的分枝(配置数据大于下界)或剪枝(重配置为较小的值);
3) 验证:当某个叶子节点的域中所有的可变点实例都已被配置时,该叶子节点便可以验证且其验证值会向上传播,直到无法继续传播.每个根节点的值代表了相应约束的验证值.true代表当前配置数据符合该条约束;false表示当前配置违背了该条约束;而undefined表示由于某些可变点实例的值尚未配置,该条约束的验证值还不确定.
1.4 Zen-Fix框架为了将不一致性修复问题转化为带约束的多目标搜索问题进行求解,需解决以下两个问题:
(1) 多目标搜索问题编码:首先是定义启发式搜索目标;其次,由于不一致修复问题是在交互配置过程中动态构建的,为了提高搜索的效率,需要最小化问题决策变量和约束集,以降低搜索过程中反复验证的代价,因此,比较关键的问题是如何动态构建决策变量以及搜索问题的约束集;
(2) OCL约束求解:在搜索不一致配置的修复方案时,搜索问题中的约束不是一般搜索问题中较常用的数学公式,而是复杂的OCL约束集,因此,如何在搜索过程中计算个体解方案对OCL约束集的违背程度,也是所面临的一个挑战.
针对以上问题,本文作者前期提出一种基于多目标搜索的配置修复推荐框架Zen-Fix[13],其主要思路可以归纳为:
(1) 定义了交互式产品线配置过程中配置修复方案的启发式优化指标,以从整体上提高配置效率;通过定义约束闭包来动态构建最小的约束集合和搜索变量,以降低搜索的复杂度,提高搜索效率;
(2) 结合前期在交互配置过程中对OCL进行增量验证的工作(见第1.3节),融合对OCL违背距离的计
算[14],增量获取个体解决方案(即一组配置数据)对OCL约束集的违背距离.
2 问题定义根据前文的分析可知,交互配置中的不一致性修复主要面临以下3个挑战:(1) 保证修复方案不会引入新的不一致;(2) 保证修复方案在所有可行方案中最优;(3) 保证不一致修复的时间效率.为了应对以上挑战,鉴于基于搜索的技术在软件工程领域的成功应用和巨大潜力,本文将不一致性修复问题转化为带约束的多目标搜索问题,通过设计高效的搜索算法实现不一致性修复方案的推荐.为了实现搜索问题的构建,第2.1节给出了基本概念,第2.2节定义了本文的多目标搜索问题.
2.1 基本概念在产品配置过程中,一个特定产品模型可以表示为VPT={{VPC},{VPUN}},其中,VPT表示该产品所有的可变点(实例),VPC表示所有已经配置的可变点实例,而VPUN表示所有未配置的可变点或可变点实例.随着产品的配置进行,VPC的数量不断增加,直到VPUN变为空,则表示整个产品配置完成.一个可变点实例的类型可以有以下4种,可变点类型={基数,类型,属性,拓扑}.对某个可变点实例的配置即是对配置参数赋值的过程,配置的值称为配置数据,该配置数据属于以下5种基本数据类型,配置数据类型={Integer,Real,String,Enumeration,Boolean}.每个可变点实例有唯一的标识,是一条从产品线模型根节点到当前可变点实例的路径.比如,root::XmasTree[2]:: sensors表示的是第2个XmasTree上的可变点实例sensors,即传感器个数.可变点实例是在配置过程中动态产生的,Zen-CC会动态地为每个新实例化的可变点生成标识.
信息物理系统产品线体系结构模型预定义约束(一致性约束)可以表示为CRT={cr1,cr2,cr3,…,crncr},其中,ncr是总的约束数目.在配置过程中,当一条约束被违背时即为产生一个不一致.对于产生的所有不一致,可以表示为NCon={ncon1,...,nconnvr},意味着分别违背了以下的约束CRV={vcrv1,…,vcrnvr},其中,nvr(nvr≥1)为违背的约束总数,且CRV $\subseteq $ CRT.为了保证修复不一致的同时不会引入新的不一致,显然,在搜索的过程中只考虑CRV中的约束是不够的,因为修复方案可能会违背在CRT而不在CRV中的约束;另一方面,如果考虑CRT中所有的约束,意味着要反复验证很多不相干的约束和决策变量(即可变点实例)而降低搜索的效率.因此,问题的关键是需要找到一个最小的约束集合,使得在保证搜索效率的同时又能保证不会引入新的不一致.我们将这个最小的约束集合定义为闭包.在给出闭包定义之前,先给出以下基本概念:
$\bullet $ 对于约束cri,Config(cri)表示被cri约束的所有的已经配置的可变点实例;
$\bullet $ 对于约束集CRi={cr1,cr2,…,crn},Config(CRi)=Config(cr1) $\cup $ Config(cr2) $\cup $ … $\cup $ Config(crn)表示所有的被约束集中的约束所约束的已经配置的可变点实例的集合;
$\bullet $ 对于一个已经配置的可变点实例vpi,Scope(vpi)表示所有与该可变点实例相关的约束;
$\bullet $ 对于一系列的可变点实例的集合VPi={vp1,vp2,…,vpn},Scope(VPi)=Scope(vp1) $\cup $ Scope(vp2) $\cup $ … $\cup $ Scope(vpn)表示与VPi中所有可变点实例相关的约束的集合;
$\bullet $ 对于一条违背的约束vcrvi,将为修复违背该约束的配置数据所需要考虑的最小约束集定义为Closure(vcrvi).可证明:当且仅当Closure(vcrvi)满足vcrvi $\in $ Closure(vcrvi) $\cap $ Scope(Config(Closure(vcrvi)))= Closure(vcrvi)时,Closure(vcrvi)为最小约束集;
$\bullet $ 类似地,对于违背的所有约束CRV,其闭包可以表示为
Closure(CRV)=Closure(vcrv1) $\cup $ … $\cup $ Closure(vcrnvr).
如图 3所示,为计算约束vcrvi的闭包Closure(vcrvi)算法.Closure(vcrvi)初始值只包含约束vcrvi,在计算闭包的过程中,迭代地将CRT中不属于闭包Closure(vcrvi)且与Closure(vcrvi)存在共同的已配置可变点实例的约束加入到闭包中.类似地,可以计算所有违背约束CRV的闭包Closure(CRV).
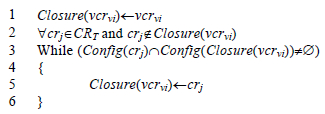
|
Fig. 3 Algorithm of calculating the closure of one violated constraint 图 3 单个违背约束的闭包计算算法 |
满足约束的配置数据可能存在成百上千种可能,但是就整个产品的配置效率而言,这些配置却并不是等价的.因此,为了找到最优的满足约束的配置数据,本文针对影响整个配置效率的因素定义了一系列度量指标.这些指标分为两类:{CostMeasure,EffectivenessMeasure},其中,CostMeasure表示一系列与成本相关的指标,而EffectivenessMeasure表示与效益有关的指标.
为解决配置的不一致性修复问题,将其转化为一个带约束的多目标优化问题.多目标为本文定义的两类度量指标:{CostMeasure,EffectivenessMeasure},约束为由所有违背约束产生的闭包Closure(CRV),搜索问题的决策变量即为该闭包内所有的已配置可变点实例Config(Closure(CRV)),而搜索问题的一个解代表着对所有决策变量的一次赋值,相应于一组对Config(Closure(CRV))中部分(或全部)可变点实例的重配置数据.
为了将搜索问题均一化为最小化问题,与成本指标CostMeasure相关的函数定义为与指标单调性一直的函数Fcost,而与效益指标EffectivenessMeasure相关的函数定义为与指标单调性相反的函数Feffective.因此,这个带约束的多目标优化问题可以描述如下:
$$\begin{array}{l} \min y = ({F_{cost}},{F_{effective}}) = ({f_{cos{t_1}}}(x),...,{f_{cos{t_m}}}(x),{f_{effectiv{e_1}}}(x),...,{f_{effectiv{e_n}}}(x))\\ x = ({x_1},...,{x_k}),{x_i} \in Config(Closure(C{R_V}))\\ x{\rm{ s}}{\rm{.t}}{\rm{. }}Closure(C{R_V}) \end{array}$$ 3 面向配置修复的多目标搜索算法为了实现最优的修复方案推荐,第3.1节首先介绍了Zen-Fix定义的交互配置过程中一致性修复的优化目标;在本文所要解决的搜索问题中,约束并非传统多目标搜索问题中的数学公式,而是具有复杂结构且相互关联的OCL约束,这为多目标搜索带来了很大的挑战,第3.2节中介绍了Zen-Fix采用的约束求解技术;最后,为了保证搜索的效率和搜索性能,提高Zen-Fix的实用性,第3.3节介绍了本文提出的搜索算法DeIBEA.
3.1 多目标Zen-Fix为成本定义了3个指标,分别为修复的可变点实例的数目(FNUM)、修复方案对整个配置过程的影响(FIMPACT)以及对未配置可变点实例进行约束验证的花销(FCC).此外,为效益定义了一个指标,即,可以推理的可变点实例的程度(FINFER).
3.1.1 最小化修复的可变点实例数目修复的可变点实例的数目越多,存在的潜在的影响越大,因此在Zen-Fix中定义最小化修复的可变点实例数目为其中一个成本指标.对某个修复方案Sop来说,该指标定义如下:
$${F_{NUM}} = NumVP\left( {{S_{op}}} \right)/NumVP\left( {Config\left( {Closure\left( {C{R_V}} \right)} \right)} \right),$$其中,NumVP(Sop)表示修复方案中修复的可变点数目;而NumVP(Config(Closure(CRV)))表示可能修复的可变点实例个数,即,所有的决策变量数目.
3.1.2 最小化修复对整个配置过程的影响根据被修复的可变点实例类型的不同,其对整个产品配置的影响也有所不同,主要体现在对未配置可变点的影响上.例如,对于基数可变性而言,修复该类型的可变点实例可能会引入新的可变点实例(值增加时)或者删除某些已有的可变点实例(值减少时),从而会改变整个产品的体系结构.而在大规模信息物理系统产品线配置过程中,这往往是不被期望的.因此,最小化配置修复对整个产品配置影响是Zen-Fix中定义的第2个成本指标.
本文根据可变点实例类型的不同,将修复单个可变点实例vpi的影响定义如下:
$${F_{IMPACT}}(v{p_i}) = \left\{ {\begin{array}{*{20}{l}} {{f_i} \times |s{v_i} - i{v_i}|,{\rm{ where }}v{p_i}.VPType = Cardinality}\\ {{f_i},{\rm{ where }}v{p_i}.VPType = \{ Topology,Type\} }\\ {1,{\rm{ where }}v{p_i}.VPType = Attribute} \end{array}} \right\},$$其中,fi为影响因子.对于基数可变性来说,fi的值是基于整个产品线模型的层次结构计算得到的,它等于当相应可变点实例变化为1时所引入/删除的其他可变点实例的个数.svi表示修复方案中该可变点实例修改后的值,而ivi表示修复之前的初始值.因此,修复一个基数可变点实例的影响为该可变点的影响因子乘以该可变点的变化值.对拓扑可变性和类型可变性的配置,是通过从一系列预定义的选项中选择一种拓扑结构或者一种子类型而完成的,对这两类可变点的影响因子fi定义为为了选择的更改而引入或删除的可变点实例的个数.因此对于不同的选择,fi的值不同.对于属性类型的可变点实例,其影响因子fi的值均为1,因为更改属性可变性不会对整个产品的体系结构产生影响.
假设一个修复方案包含以下可变点实例的修复,即{vp1,vp2,…,vpn}.基于单个可变点实例的影响,可以计算出该修复方案对整个产品配置的影响为 ${F_{IMPACT}} = \sum\nolimits_{j = 1}^n {{F_{IMPACT}}(v{p_j})} .$ 为了方便结果的处理,采用文献[15]中的方式对该函数进行均一化为 ${F_{IMPACT}} = \sum\nolimits_{j = 1}^n {{F_{IMPACT}}(v{p_j})/(1 + \sum\nolimits_{j = 1}^n {{F_{IMPACT}}(v{p_j})} )} .$
3.1.3 最小化约束验证的代价如第1.3节所述,对于一条约束而言,即使其相关的可变点实例并未全部配置,其仍然可以为true.这意味着对与该约束相关的未配置可变点实例的配置并不会影响约束的最终结果.基于此,在配置这些可变点实例时,就可以省去不必要的约束验证以提高整个配置的效率.例如,对于约束A or B,A和B都是布尔表达式,当A的值为true而B的值为undefined时,整个约束为true,此后,对与B相关的未配置可变点实例进行配置并不会影响整个约束的结果.因此,对B的验证可以省去.最小化约束验证的代价是Zen-Fix中定义的第3个成本指标,其定义如下:FCC=1-NUMsave/(1+NUMsave),其中,NUMsave表示约束验证中可以忽略的约束表达式的个数.
3.1.4 最大化可以推理的可变点实例我们的前期工作[16]指出:某些约束在特定的情况下,可以用于自动推理.最大化可以推理的可变点实例个数可以最大程度地提高整个产品的配置效率,因此,Zen-Fix将效益指标定义为可以在可变点实例中进行推理的比例,即:
$${F_{INFER}} = NU{M_{INFER}}/NU{M_{TOTAL}},$$其中,NUMINFER指的是可以推理的可变点实例的个数,而NUMTOTAL表示与Closure(CRV)有关的所有未配置的可变点实例的个数.
3.2 约束求解对于带约束的多目标优化问题,约束处理的前提是获得搜索过程中每个个体对约束的违背程度.首先,不同于一般的直接用数学公式表达的约束形式,在本文的问题中,需要获得每种配置方案对复杂OCL约束的违背程度;其次,由于本文面向的是交互式配置过程,因此对系统的时间性能有较高的需求,而对约束违背程度的计算方法是在搜索过程中被反复调用的,因此,该方法的效率对整个系统的时间性能有至关重要的影响.
文献[14]中,基于OCL定义了一系列启发式策略以引导搜索算法对OCL的求解过程,最终获得满足OCL约束的测试数据.该启发式策略定义了一组输入数据对OCL约束的违背程度,其思路来自对源代码的分支距离启发策略[17].例如,对于约束x=0,有两组输入数据x1:=5和x2:=100.第1组数据对该约束的违背距离比第2组数据对该约束的违背距离要小.如第1.3节所述,在作者前期工作中,提出了一种增量OCL验证的方法Zen-CC,基于交互配置过程产生的配置数据,对OCL进行局部验证以增量获取OCL验证结果(即true,false或undefined).已经证明:Zen-CC的效率在10ms以内,具有较高的时间性能.为了实现高效的对约束距离的求解,Zen-Fix借鉴文献[14]中对OCL约束违背距离的定义对Zen-CC进行改进,大体思路是:使得每个节点在验证的同时也计算出配置数据对该节点的违背距离,该距离可以随着验证结果向上传播,在根节点处可以同时获得整个约束的验证结果以及违背距离.
在配置修复构成带约束多目标优化的问题中,要考虑的约束为Closure(CRV),Zen-Fix定义一个修复的方案SI对整个约束集的违背距离为
$${F_{DISTANCE}} = \sum\nolimits_{i = 1}^{\# {\rm{ }}of{\rm{ }}Closure(C{R_V})} {BranchDistance({S_{\rm{I}}},C{R_i})/\# {\rm{ }}of{\rm{ }}Closure(C{R_V})} ,$$其中,约束CRi $\in $ Closure(CRV),且BranchDistance(SI,CRi)表示解SI对约束CRi的违背距离.当违背距离FDISTANCE为0时,表示当前修复方案符合所有约束.
3.3 DeIBEA算法传统的IBEA算法采用最简单且比较常用的约束处理技术作为约束优先原则,即:如果一个是可行解,一个是不可行解,则可行解获胜;如果两个都是可行解,则拥有较小目标函数的获胜;如果两个都是不可行解,则违背约束小的解获胜.但是这种方式的问题在于,没有很好地利用边界的不可行解,使得优化的效果很差.此外,不同于这种严格的比较关系,可以通过引入惩罚机制来对不可行解进行惩罚.但这类方法进化压力较大,收敛性好而种群多样性却较差[18].考虑到约束多目标问题的最优解往往存在于可行域的边界,而可行域的不连通性使得不可行解往往是通向最优解的桥梁,因此在搜索过程中,不可行解的作用是不容忽视的.鉴于此,DeIBEA算法通过区分可行解和不可行解,并引入差分算子来最大限度地挖掘不可行解和可行解之间的边界.
DeIBEA的算法流程如图 4所示.该算法的特点是在执行过程中分别维护两个解集合,即,可行解集合与不可行解集合,父母通过一定的概率从两个解集中选取,并通过对父母的差分产生后代.该算法主要有以下几个迭代步骤:

|
Fig. 4 Pseudo code for DeIBEA algorithm 图 4 DeIBEA算法伪代码 |
1) 初始化可行解集与不可行解集(图 4第1行~第9行);
2) 首先,从可行解集中选择一个父母;然后,从不可行解集中选择另外一个父母,利用差分算子对两个父母进行交叉产生后代(图 4第12行~第15行);
3) 每次产生的后代,先判断其为可行解还是不可行解.如果是可行解,则与父母中的可行解相比,如果比父母优,则替代父母;如果比父母劣,则遗弃;否则,加入到可行解集合中.如果是不可行解,则与父母中不可行解一方进行比较,操作类似(图 4第16行~第28行);
4) 如果可行解集(不可行解集)个体个数大于集合容量,则采用基于指标的方式计算每个个体的适应度,并逐步去除具有最差适应度的个体,直到满足容量(图 4第31行~第36行).
该算法的优势在于:首先,采用可行解与不可行解差分的方式,可以充分挖掘两个解集之间的边界值,因为对于带约束的多目标搜索问题,最优解往往会分布于边界上;其次,DeIBEA算法通过替代策略可以加快其收敛速度,而且提高运行效率,因为这样可以降低基于指标进行适应度的复杂计算次数.
4 案例研究本节通过海底油气领域中一个实际的工业案例,对Zen-Fix的有效性进行验证.第4.1节首先介绍了案例描述,随后分别对实验设计(第4.2节)和执行(第4.3节)进行了介绍,之后对结果进行分析和讨论(第4.4节),最后对结果的有效性风险进行了分析(第4.5节).
4.1 案例描述海底采油控制系统通过海底各种传感器采集数据,并控制海底采油树进行油井生产的管理.海底采油控制系统是一种高度可配置系统,往往存在成百上千的可变点,例如传感器的参数配置、海底采油树上各种阀门的配置以及采油树的部署配置等.可变点之间又存在诸多复杂的依赖约束,如图 1所示.
本文对ISO 136286:2006标准[19]中海底采油控制系统产品线的主要概念采用SimPL建模语言进行描述,之后,又基于该领域的工程手册[20]对模型进行扩展,得到海底采油控制系统产品线模型.该模型共包含13个包、71个类、111个可变点(包含13个基数可变性、91个属性可变性、7个类型可变性)以及25条一致性约束(OCL约束).
4.2 实验设计 4.2.1 研究问题Zen-Fix旨在为交互式信息物理系统体系结构产品线配置过程中出现的不一致提供高效且优化的修复方案推荐.Zen-Fix的有效性首先体现在是否可以自动化地推荐不一致问题的修复方案以及推荐的方案是否较优.此外,由于交互式配置过程对时间性能有较高的要求,因此时间性能优劣也是检验Zen-Fix是否可在实际产品配置过程中得到成功应用的一个重要指标.为了验证Zen-Fix与DeIBEA算法的有效性,本文定义了如下两个研究问题:
RQ1:本文提出的DeIBEA算法是否比原始的IBEA算法具有更高的效率,即,花费更少的时间?
RQ2:本文提出的DeIBEA算法是否比原始的IBEA算法具有更高的搜索性能,即,可以产生更优的解?
4.2.2 实验设计如第1.1节所述,信息物理系统产品线模型共包含4类可变点,即:基数可变性、类型可变性、属性可变性以及拓扑可变性.基于不同的可变点类型,具有两种不同的配置形式,其中,类型可变性、拓扑可变性以及属性可变性中的枚举类型都是通过从预定义的值域列表中进行选择(选择型)的,而基数可变性以及其他的属性可变性需要用户(或者配置工具)为参数进行赋值(参数型).
为了在实际海底采油控制系统产品线配置中评估对比不同的算法在解决一致性修复问题中的优劣,本文模拟一个完整的产品配置过程,并在配置过程中控制不一致问题的产生,保证配置过程的可重复性,即,在特定的配置步骤可以反复产生相同的一致性修复问题.本文实验设计包含以下几个阶段.
1) 定义配置过程:针对某个特定产品的海底采油系统的配置数据,模拟一个完整的配置过程,该过程包含一系列配置步骤,每个配置步骤是一个三元组,即 $\left\langle {} \right.$ 配置步骤,可变点实例,配置数据 $\left. {} \right\rangle $ ,相应于对一个可变点实例赋值.如, $\left. {} \right\rangle $ 10,root::XmasTree[2]::sensors,9 $\left\langle {} \right.$ 表示在配置步骤10将可变点实例root:: XmasTree[2]::sensors的值配置为9;
2) 定义不一致性的植入位置(配置步骤):对于一条一致性约束CRj,与其相关的可变点实例集合可以通过每个可变点实例相应的配置步骤的集合表示,记作{CSi,…,CSn},其中,i表示相应的配置步骤.本文将相关配置步骤的最大值n作为CRj的不一致性植入位置.如图 5所示,对于第1个一致性约束CR1,其相关的配置步骤为{CS1,CS6}(图中灰色单元格所示),则第6个配置步骤CS6为CR1的不一致性植入位置(后文简称植入位置,图中红色对勾所示);

|
Fig. 5 Strategies to generate nonconformities 图 5 不一致性问题生成策略 |
3) 定义边界值:针对每条一致性约束中关联的可变点实例的类型,基于边界值等价划分标准为每个可变点实例定义边界值.比如对于参数型的可变点,如基数可变性“1...*”,对其进行边界值等价划分可以得到两个分区:一个是≤1,另一个是≥1.对于第1个分区,考虑到基数可变性只能取非负整数,该分区内只有一个边界值为0;对于第2个分区,采用1,5,10,20 作为边界值.对于选择型的可变点,即类型、拓扑以及枚举型的属性可变性,所有的选择项都定义为其边界值;
4) 定义配置数据:为了更全面、更系统地验证Zen-Fix对不一致问题的修复能力,对于每一个植入位置,本文基于步骤3)定义的边界值考虑了相关已配置可变点实例配置数据的所有可能组合.鉴于一致性约束之间的相互关联性,对于每一个一致性约束CRj的植入位置,不仅需要考虑与CRj相关的已配置可变点实例的配置数据,因为这样可能会不可控地违背其他的一致性约束,因此还需要考虑与CRj相关的所有一致性约束,即Closure(CRj)(定义见第2.1节).如图 5所示,对于约束CR1,其植入位置为CS6,如图中红色对勾所示.在配置步骤6,需要考虑Closure(CR1)中的所有约束,即{CR1,CR2,CR3,CR5}(配置步骤第6列所有对勾所对应的一致性约束集合).本文的配置数据定义为与Closure(CRj)相关的已配置可变点实例边界值的所有组合,即,需要考虑与配置步骤{CR1,CR2,CR3,CR5}相应的4个可变点实例边界值的所有组合.
在每个植入位置,会遍历所有已配置的相关可变点实例的边界值组合进行一致性约束的检验,每个会产生不一致的组合即构成一个不一致修复问题.通过以上步骤,本文共获得10 189个不一致修复问题.基于这10 189个修复问题,本文采用IBEA和DeIBEA各运行30次以降低搜索算法中随机带来的影响.对于运行次数的选取在文献[21]中已有充分讨论,本文选择运行30次是综合考虑整体运行时间和统计分析有效性而决定的,也是基于搜索的软件工程中经常采用的实验设置[21].
4.2.3 度量指标针对第1个研究问题,本文定义了一个度量指标,即,每个算法修复不一致问题i所需要的平均时间Timei:
$$Tim{e_i} = \sum\nolimits_{j = 1}^{30} {Tim{e_{ij}}/30} ,$$其中,Timeij表示第j次修复不一致问题i所花费的时间,其中,j≤30而且i≤10189.
如第3.1节所示,对于一致性修复所构成的多目标搜索问题,本文共定义了4个启发式优化目标,即:FNUM,FIMPACT,FCC,FINFER.为了比较不同算法的搜索能力,基于这4个优化目标,本文为第2个研究问题定义了以下7个度量指标:
1) ${F'_{NU{M_{ij}}}}$ :表示每种算法第j次修复不一致问题i时所得到的多个解中的FNUM最小值;
2) ${F'_{IMPAC{T_{ij}}}}$ :表示每种算法第j次修复不一致问题i时所得到的多个解中的最小的FIMPACT值;
3) ${F'_{C{C_{ij}}}}$ :表示每种算法第j次修复不一致问题i时所得到的多个解中最小的FCC值;
4) ${F'_{INFE{R_{ij}}}}$ :表示每种算法第j次修复不一致问题i时所得到的多个解中FINFER的最小值; 这4个指标能够对比不同算法在单个优化方向上的搜索能力.
5) ${F'_{OVERAL{L_{ij}}}}$ :表示每种算法第j次修复不一致问题i时所得到的多个解中4个优化目标平均值的最小值,该指标度量了算法在各个方向上的平均搜索能力;
6) HVij:表示每种算法第j次修复不一致问题i时所得到解集的超体积(hypervolume),其中,超体积指标HV[22]表示算法所获得的Pareto前端在目标域中覆盖的体积,HV越大,表明Pareto解集在真实前端覆盖的范围越大,算法具有较好的扩展性和分布性;
7) EPSILON[22]指标用来表示算法的收敛性能,该指标越小,说明算法的收敛速度越快,EPSILONij表示算法第j次修复不一致问题i时的收敛性.
4.2.4 统计分析为了对比分析两种不同算法DeIBEA与IBEA,本文采用Wilcoxon符号秩检验[23]和Vargha与Delaney统计[24]来对度量指标进行分析.通过Wilcoxon符号秩检验来获得以0.05为显著性水平的p值,代表两种算法差异的显著性.Vargha与Delaney统计(<12)是一种非参数效应量(effect size)度量方法.在本文中,<12用于表示对于第4.2.3节中定义的某一个度量指标:<12小于0.5,表示算法IBEA比DeIBEA具有更高的概率获得较大的指标值;<12等于0.5,表示两种算法是相当的;<12大于0.5,表示算法DeIBEA比IBEA具有更高的概率获得较大的指标值.
4.3 执 行本文选用jMetal中的IBEA算法与本文设计的DeIBEA算法进行对比.通过模拟真实案例下的整个配置过程,Zen-Fix分别采用DeIBEA与IBEA两种算法对整个配置过程中植入的10 189个不一致问题进行修复,针对两种算法对整个配置过程分别模拟30次,并记录Zen-Fix在修复每一个问题时所花费的时间.IBEA算法采用jMetal的默认配置,DeIBEA算法采用与IBEA类似的设置,具体的算法设置参数见表 1.
| Table 1 Parameterization for IBEA and DeIBEA 表 1 算法IBEA与DeIBEA参数设置表 |
为了回答以上两个研究问题,本文对第4.2.3节中定义的度量指标进行Wilcoxon秩检验和Vargha与Delaney统计,结果见表 2.以时间Time为例,对于问题i,DeIBEA算法和IBEA算法各自运行30次分别得到30个数据Timeij(j≤30).对两种算法的两组Timeij值进行Wilcoxon秩检验和Vargha与Delaney统计,根据<12与p值的大小,将问题分为3大类、6小类.在此需要说明的是:在这些度量指标中,HV的值越大越好;对于其他度量指标而言,值越小越好.表 2已经对这种不同进行了处理,其中,DeIBEA>IBEA对应的列表示对于每一个度量指标,DeIBEA与IBEA相比性能较优的情况,每个单元格斜线后面的数据表示DeIBEA比IBEA性能较优的问题个数(以Time为例,表示<12<0.5),而相应单元格中斜线前的数据表示DeIBEA显著比IBEA较优的问题个数(<12<0.5且p<0.05).DeIBEA<IBEA列类似,表示DeIBEA与IBEA相比性能较差的情况.对于DeIBEA=IBEA这一列来说,斜线前的数据表示DeIBEA与IBEA相比没有显著性差异的问题个数(p≥0.05),而斜线后面的数据记录了DeIBEA与IBEA表现相同的问题个数(<12=0.5).
| Table 2 Wilcoxon秩检验和Vargha与Delaney分析结果 ${F'_{IMPACT}}$ 表 2 Results of the Wilcoxon signed-rank test and the Vargha and Delaney statistics |
RQ1:如表 2第1行所示:对于产生的10 189个不一致修复推荐问题,有10 170个问题DeIBEA算法消耗的时间小于IBEA,其中,对9 244个问题的修复DeIBEA所用的时间显著小于IBEA算法;仅仅有14个问题IBEA消耗时间小于DeIBEA,但是它们之间的差异并不显著;共有945个不一致问题在修复的时候,DeIBEA与IBEA的时间性能没有显著性差异,其中有5个问题DeIBEA与IBEA所用时间完全一样.此外,本文还对每种算法对问题i的平均时间Timei进行了统计.如表 3所示:对于所有的10 189个问题,DeIBEA运行时的最大平均时间是4 668ms,最小平均时间是614ms,平均平均时间是3 263ms;而IBEA分别为6 371,1 529和4 664ms.在交互式产品线配置过程中,系统的响应时间是决定其实用性的重要因素.因此,修复不一致问题所需要的时间是决定Zen-Fix成功与否的关键因素.通过以上分析结果可知,本文提出的改进算法DeIBEA较原来的IBEA算法具有更高的时间性能,可以更大程度地提高Zen-Fix进行不一致修复的效率.
| Table 3 Time performance for DeIBEA and IBEA 表 3 算法DeIBEA与IBEA时间性能 |
RQ2:为了对比两种算法的搜索性能,本文对另外7个度量指标进行Wilcoxon秩检验和Vargha与Delaney
统计,统计分析的方法与上文对时间指标Time的方法类似,分析结果见表 3.对于前两个度量指标 ${F'_{NUM}}$ 与 ${F'_{IMPACT}}$ ,分析结果比较类似.对于 ${F'_{NUM}}({F'_{IMPACT}})$ 来说,10 189个问题中:5 228(5 228)个问题的搜索结果是DeIBEA
优于IBEA,其中,2 552(2 518)个问题下,DeIBEA显著占优;3 960(3 960)个问题的搜索结果是IBEA优于DeIBEA,但是只有764(765)个问题是IBEA显著占优的.对两种算法来说,没有显著性差异的问题个数为6 873(6 906),其中,1 001(1 001)个问题两种算法的搜索结果完全相同.以上数据可以说明:针对前两个优化目标,即最小化修复的可变点实例与最小化修复对未配置可变点的影响,DeIBEA算法较之IBEA算法在更多的问题上具有更好的搜索能力,可以搜索到更优的解.
对于第3个度量指标 ${F'_{CC}}$ ,有10 181个一致性修复问题,两种算法的搜索结果没有显著性差异.这可能是由
于,在此优化方向上,解空间中各个解本身对约束验证代价的影响的差异性较小造成的.对于第4个度量指标 ${F'_{INFER}}$ ,10 189个问题中有10 175个问题,DeIBEA的搜索结果比IBEA要更优,对于其中9 081个问题,DeIBEA
具有显著性的优势.在第4个优化方向上,DeIBEA远远优于IBEA的搜索性能.
对于第5个度量指标 ${F'_{OVERALL}}$ ,体现了搜索算法在各个方向上的平均搜索性能.由表 3可以看出:有将近一半(5 263)的问题,DeIBEA优于IBEA算法,即,可以得到更小的平均适应度值.其中,在2 548个问题上,DeIBEA显著优于IBEA算法.而IBEA算法只在762个问题上显著优于DeIBEA.总体上来说,针对平均搜索性能,DeIBEA稍微优于IBEA算法.
对于第6个度量指标超体积HV,有9 635个问题DeIBEA优于IBEA.其中,1 858个问题中,DeIBEA显著占优;而IBEA仅仅在13个问题上显著优于DeIBEA,远远小于其显著劣于DeIBEA的问题个数(1 858).分析结果说明,DeIBEA算法较之IBEA算法具有更好的扩展性和分布性.
对于评估收敛速度的度量指标EPSILON,对于9 574个问题,DeIBEA的收敛速度快于IBEA,其中,有5 660个问题DeIBEA的收敛速度显著快于IBEA;而IBEA的收敛速度只在455个问题上优于DeIBEA,其中只有8个问题是显著占优.通过以上分析很容易得出结论:DeIBEA的收敛速度与IBEA相比具有明显的优势.
通过以上实验分析,我们可以得出以下结论:
1) 本文提出的DeIBEA算法比原始的IBEA算法具有更好的效率;
2) 本文提出的DeIBEA算法比原始的IBEA算法具有更好的搜索性能.
4.5 有效性风险可能的内部有效性风险在于本文对两种算法的参数设置.为了降低这种风险的可能性,本文对传统的IBEA算法采用默认的配置,并对DeIBEA算法采用相同的参数配置.外部有效性风险主要存在于对实验结果的普适化.本文通过对一个工业案例配置过程进行模拟,生成了10 189个不一致性修复问题,因此,本文的实验结果可以在一定程度上进行泛化.但是,为了更进一步地验证本文结果的普适性,需要更大规模的案例以及更多的修复问题.
5 结 论在信息物理系统产品线的交互配置过程中,人工的配置难免引入配置的不一致性,即,配置违背了预定义的约束.而信息物理系统本身的复杂性和约束密集性,为不一致修复带来了很大的挑战.本文将不一致修复问题转化为带约束的多目标搜索问题:首先,面向配置效率定义了4个优化目标以启发搜索过程;并基于前期增量验证的工作实现了增量约束(OCL)违背距离求解.通过多目标搜索算法,为用户推荐较优的修复方案.
IBEA算法在产品线配置(多为特征选择)中已经得到成功运用,但本文工作的不同之处在于:首先,本文面向的是交互式产品线配置,为不一致修复的时间性能带来了很高的需求,IBEA算法由于其本身运算的复杂度导致时间性能不高;其次,信息物理系统产品线中约束较为复杂,IBEA算法中采用的占优方式不能很好地利用不可行解,从而会影响算法的搜索性能.基于以上两点,本文通过将差分进化算法引入到IBEA算法中,并区分可行解与不可行解,提出了改进的DeIBEA算法,通过工业案例的实验,其结果表明,DeIBEA算法无论从时间性能还是搜索性能上都优于传统的IBEA算法.
| [1] | Rajkumar RR, Lee I, Sha L, Stankovic J. Cyber-Physical systems: The next computing revolution. In: Cyber-Physical Systems: The Next Computing Revolution. 2010. 731-736. http://dl.acm.org/citation.cfm?id=1837461 |
| [2] | Cordy M, Schobbens PY, Heymans P, Legay A. Towards an incremental automata-based approach for software product-line model checking. In: Proc. of the 16th Int’l Software Product Line Conf., Vol.22012. 2005. 74-81 . |
| [3] | Hubaux A, Xiong Y, Czarnecki K. A user survey of configuration challenges in Linux and eCos. In: Proc. of the 6th Int’l Workshop on Variability Modeling of Software-Intensive Systems 2012. 2012. 149-155 . |
| [4] | Henard C, Papadakis M, Harman M, Le Traon Y. Combining multi-objective search and constraint solving for configuring large software product lines. In: Proc. of the ICSE 2015. 2015. http://dl.acm.org/citation.cfm?id=2818819 |
| [5] | Zitzler E, Künzli S. Indicator-Based selection in multiobjective search. In: Indicator-Based Selection in Multiobjective Search. 2004. 832-842 . |
| [6] | Behjati R, Yue T, Briand L, Selic B. SimPL: A product-line modeling methodology for families of integrated control systems. Information and Software Technology, 2013,55(3):607-629 . |
| [7] | OMG. OCL 2.0 Specification. 2005. |
| [8] | Sayyad AS, Ingram J, Menzies T, Ammar H. Scalable product line configuration: A straw to break the camel’s back. In: Scalable Product Line Configuration: A Straw to Break the Camel’s Back. 2013. 465-474 . |
| [9] | Storn R, Price K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997,11(4):341-359 . |
| [10] | OMG. UML 2.2 Superstructure Specification (formal/2009-02-04). 2009. |
| [11] | Stoiber R, Glinz M. Supporting stepwise, incremental product derivation in product line requirements engineering. System, 2010,1:2. |
| [12] | Hong L, Tao Y, Ali S, Kunming N, Li Z. Zen-CC: An automated and incremental conformance checking solution to support interactive product configuration. In: Proc. of the IEEE 25th Int’l Symp. on Software Reliability Engineering (ISSRE). 2014. 13-22 . |
| [13] | Hong L, Yue T, Ali S, Li Z. Integrating search and constraint solving for nonconformity resolving recommendations of system product line configuration. In: Proc. of the IEEE Int’l Conf. on Software Testing, Verification and Validation (ICST). 2016. |
| [14] | Ali S, Iqbal MZ, Arcuri A, Briand L. Generating test data from OCL constraints with search techniques. IEEE Trans. on Software Engineering, 2013,39(10):1376-1402 . |
| [15] | Arcuri A. It really does matter how you normalize the branch distance in search-based software testing. Software Testing, Verification and Reliability, 2013,23(2):119-147 . |
| [16] | Nie K, Yue T, Ali S, Zhang L, Fan Z. Constraints: The core of supporting automated product configuration of cyber-physical systems. In: Constraints: The Core of Supporting Automated Product Configuration of Cyber-Physical Systems. 2013 . |
| [17] | McMinn P. Search-Based software test data generation: A survey. Software Testing Verification & Reliability, 2004,14(2): 105-156 . |
| [18] | Hsieh MN, Chiang TC, Fu LC. A hybrid constraint handling mechanism with differential evolution for constrained multiobjective optimization. In: A Hybrid Constraint Handling Mechanism with Differential Evolution for Constrained Multiobjective Optimization. 2011. 1785-1792 . |
| [19] | ISO 13628-6: 2006. Petroleum and natural gas industries-design and operation of subsea production systems. Standard, Part 6: Subsea Production Control Systems. 2006. |
| [20] | Bai Y, Bai Q. Subsea Engineering Handbook. Gulf Professional Publishing, 2010. https://books.google.com/books/about/Subsea_Engineering_Handbook.html?id=ZkkPos9OKDcC |
| [21] | Arcuri A, Briand L. A practical guide for using statistical tests to assess randomized algorithms in software engineering. In: Proc. of the 33rd Int’l Conf. on Software Engineering. Waikiki, 2011. 1-10 . |
| [22] | Durillo JJ, Nebro AJ. jMetal: A Java framework for multi-objective optimization. Advances in Engineering Software, 2011,42(10): 760-771 . |
| [23] | Wilcoxon F. Individual Comparisons by Ranking Methods. Springer-Verlag, 1992. 196-202 . |
| [24] | Vargha A, Delaney HD. A critique and improvement of the CL common language effect size statistics of McGraw and Wong. Journal of Educational and Behavioral Statistics, 2000,25(2):101-132 . |
 2016, Vol. 27
2016, Vol. 27


