由于在通信协议、密码安全、信息处理、分布式计算上的应用, 量子系统的推理、验证已经受到广泛的关注^[1], 特别量子系统的模型检测^[2-4].量子系统的模型检测至少需要包含3个元素:模型、属性和检测算法; 而刻画量子系统属性的逻辑工具主要有经典命题逻辑、量子逻辑、量子计算逻辑^[1].

近年来, 学者们针对不同量子系统提出了不同模型检测方法.应明生提出了利用量子自动机刻画封闭量子系统, 用闭子空间表示原子命题, 利用毕克霍夫-冯·诺依曼量子逻辑刻画量子状态的属性, 描述了量子系统的安全性、不变性、公平性等线性时间属性, 基于自动机技术给出了量子线性时间属性的检测算法^[2].关于这种量子系统的线性时序逻辑和计算树逻辑的检测仍然是公开性问题.冯元提出了利用量子马尔可夫链描述开放量子系统, 用经典的计算树逻辑描述量子状态属性, 给出了量子马尔可夫链的计算树检测算法, 并且将方法应用于检测量子BB84协议, 其中状态属性是经典的^[3].Mateus等人提出了Exogenous量子命题逻辑, 并证明该逻辑公理系统的可靠性和完备性; 构造了量子线性时序逻辑QLTL和量子计算树逻辑QCTL, 通过量子Kripke结构对封闭量子系统进行建模; 用QLTL和QCTL刻画量子状态属性, 说明了QLTL、QCTL的公式和经典的LTL, CTL公式之间的关系, 利用经典算法给出QLTL, QCTL的检测方法.这方面的工作还未涉及到用密度算子描述的开放量子系统^{[5, 6]}.

在经典迁移系统和概率系统, 可达性检测是一个关键性问题.比如:基于自动机技术的迁移系统安全性检测, 它等价于乘积系统的终状态是否可达; 强公平性检测, 它等价于状态是否是无限经常可达; 而弱公平性检测, 它等价于状态是否是最终永远可达^{[7, 8]}.在量子系统中, 同样存在着这方面的研究.文献[9]利用Bottom强连通分支(BSCC)和算子渐近平均值提出了计算量子马尔可夫链的可达性、重复可达性、一致可达性概率的方法.文献[10]研究了量子系统的可达性的可判定性问题.文献[11]研究了递归式量子马尔可夫链的可达性分析.

本文首先回顾几种量子马尔可夫链模型; 其次构建Exogenous量子算子逻辑, 该逻辑是可靠完备的; 接着给出检测量子算子公式可满足性的复杂度; 然后, 在Exogenous量子算子逻辑基础上定义Exogenous量子马尔可夫链, 提出几种常用的可达性, 分析可达性公式的可满足性问题和可判定性问题; 最后, 通过实例说明Exogenous量子马尔可夫链及其可达性与广义量子Loop程序终止问题的关系.

1 符号规定

设n个单量子比特构成的集合qB={qb₁, qb₂, …, qb_n}, H_qB表示赋值集2^qB张成的Hilbert空间, 即:

${H_{qB}} = span\{ |\left. v \right\rangle |v \in {2^{qB}}\} .$

将qB看作是量子命题变元集, 任意子集A⊆qB都有唯一基向量与其一一对应, 当qb∈A时, 赋值为真; 当qb∉A时, 赋值为假.设B(H_qB)为H_qB上有界线性算子, P(H_qB)={P∈B(H_qB)|P=P=P²}为H_qB上的投影算子, D(H_qB)={ρ∈B(H_qB)|t(ρ)ρ=1}为H_qB上的量子密度算子.

2 Exogenous量子马尔可夫链

量子马尔可夫链已经被学者们所研究, 它主要用来刻画量子系统的动态演化^[12-14].量子行走是一类特殊的量子马尔可夫链, 得到广泛关注, 已经成功应用于设计和分析量子算法^{[15, 16]}.文献[17]将量子马尔可夫链定义为二元组 < G, ε > , G是有向图, ε=[ε_ij]是迁移算子矩阵(TOM).矩阵TOM的每一个元素ε_ij标签为点i到点j的边, 它满足完全正性, 且每列的和为一个量子运算.该量子马尔可夫链给出量子系统状态转移的特性, 每一个节点代表一个状态, 但状态是经典的且状态数是有限的, 而量子系统的状态是用量子态描述且Hilbert空间是连续的.文献[9]将经典马尔可夫链 < S, P > 推广到量子情形, 定义了量子马尔可夫链 < H, ε > , 用Hilbert空间H替代状态空间S, 用超算子ε替代概率转移矩阵P, 量子状态空间是连续的.文献[3]定义了量子马尔可夫链 < S, H, Q > , 其中, S是经典状态集, H是量子状态空间, Q表示状态转移算子矩阵, 该模型采用经典命题逻辑来刻画量子系统的状态属性, 但不是用量子逻辑刻画量子态.

如何用量子逻辑刻画量子马尔可夫链的量子态, 合适的量子逻辑是关键.关于量子逻辑, 一般是指毕克霍夫-冯·诺依曼等学者提出的一类正交模格数学代数结构.然而, 文献[5]提出了基于Exogenous的量子命题逻辑, 刻画了量子态|ψ > 的属性, 同时还保持经典命题逻辑特性.不过, Exogenous量子命题逻辑系统只适合刻画量子态|ψ > , 而不适合刻画用密度算子描述的开放量子系统.针对该问题, 本文提出一种Exogenous量子算子逻辑, 记号为L_E, 并通过该逻辑描述量子马尔可夫链.

2.1 L_E的语法

Exogenous量子算子逻辑的语法由3部分组成:经典命题公式、算子项和量子算子公式.

(1)经典命题公式$\alpha : = { \bot _C}\left| {qb} \right|\alpha { \to _C}\alpha $.

由qB中的n个量子比特{qb₁, qb₂, …, qb_n}作为命题变元, ¬_C, ∨_C, ∧_C, →_C, ↔_C作为联结词.所有经典命题公式记为Γ_C.经典命题公式用来刻画经典属性.

(2)算子项$t: = O|I|x|\int \alpha |T_A^G|t + t|t \otimes t.$

算子项的论域是有界线性算子B(H_qB), 其中:O, I分别表示零算子、恒等算子; x∈X为项变元, X={x_k|k∈N}⊆B(H_qB); $\int \alpha $为概率算子项; A⊆G⊆qB; $T_A^G$为投影算子项; t+t算子和项; t⊗t张量积算子项.所有量子算子项记为Term.算子项用来描述投影测量、量子运算等.

(3)量子算子公式γ:=t≤t|⊥_Q|γ→_Qγ.

t≤t称为量子算子原子公式, 称qAtom:={t≤t}为量子算子原子命题集.⊥_Q为量子算子矛盾式, 量子算子公式是由qAtom经联结词⊥_Q, →_Q联结递归形成的公式.所有量子算子公式记为Γ_Q.称没有项变元的量子算子公式为量子算子闭式.量子算子公式用来描述测量结果的比较.

在L_E定义中有两组联结词:一组是针对经典命题公式, 一组是针对量子算子公式.在不引起歧义的条件下, 去掉下标C, Q.

关于$\int \alpha $和$T_A^G$的含义解释是:概率算子项$\int \alpha $表示使公式α为真的概率; 投影算子$T_A^G$定义为P_(∧A)G⊗I_qB/G, 其中, A⊆G⊆qB, ${( \wedge A)_G}: = \mathop \wedge \limits_{q{b_k} \in A} q{b_k} \wedge \mathop \wedge \limits_{q{b_k} \notin G\backslash A} \neg q{b_k}$, P_(∧A)G表示使公式(∧A)_G为真的赋值作为一组基向量所张成的H_G子空间上的投影算子, H_g⊆H_qB表示由2^G张成的Hilbert空间.

量子算子公式γ否定定义为¬_Q:=γ→_Q⊥_Q, 类似于经典命题公式定义下列联结词∨_Q, ∧_Q, →_Q, ↔_Q.定义t₁=t₂:=(t₁≤t₂)∧_Q(t₂≤t₁), t₁ < t₂:=(t₁≤t₂)∧_Q¬_Q(t₁=t₂), t₁ > t₂:=t₂ < t₁.统称{t₁≤t₂, t₁=t₂, t₁ < t₂, t₁ > t₂}为量子算子比较公式.设任意的γ, γ₁, γ₂∈Γ_Q, 量子算子公式γ长度或复杂度记号为|γ|, 长度|γ|递归定义为:(1) |γ|=0;(2) |¬_Qγ|=|γ|+1;(3) |γ₁→_Qγ₂|=max (γ₁, γ₂)+1.

2.2 L_E的语义

Exogenous量子算子逻辑的语义包括对经典命题公式、项和量子算子公式的解释.对于经典命题公式α, 给出qB上的赋值v∈2^qB, 记v可满足α为v⊨α, 同时记|α⊨{v∈2^qB|v⊨α}表示使α为真的赋值集.关于项变元x的解释, 定义指派函数σ:X→B(H_qB), 其中, X为所有项变元之集.给定一个量子密度算子ρ∈D(H_qB), 项和量子算子公式语义递归定义如下:

算子项的语义:

·$\left[\kern-0.15em\left[ x \right]\kern-0.15em\right] = tr(x(\rho ));$

·$\left[\kern-0.15em\left[ O \right]\kern-0.15em\right] = tr(O(r)) = 0;$

·$\left[\kern-0.15em\left[ I \right]\kern-0.15em\right] = tr(I(\rho )) = 1;$

·$ [\kern-0.15em[ \int \alpha ]\kern-0.15em] = \sum\limits_{v \in |\alpha |} {tr(P{}_v(\rho ))} $

·$ [\kern-0.15em[ T_A^G ]\kern-0.15em] = tr(T_A^G(\rho ))$, 其中, A⊆G⊆qB;

·$\left[\kern-0.15em\left[ {{t_1} + {t_2}} \right]\kern-0.15em\right] = \left[\kern-0.15em\left[ {{t_1}} \right]\kern-0.15em\right] + \left[\kern-0.15em\left[ {{t_2}} \right]\kern-0.15em\right] = tr({t_1}(\rho )) + tr({t_2}(\rho ));$

·$\left[\kern-0.15em\left[ {{t_1} \otimes {t_2}} \right]\kern-0.15em\right] = tr(({t_1} \otimes {t_2})\rho ) = tr({t_1}({\rho _1})) \times tr({t_2}({\rho _2})),其中,\rho = {\rho _1} \otimes {\rho _2}.$

量子算子公式的语义:

·ρ⊨t₁≤t₂当且仅当$\left[\kern-0.15em\left[ {{t_1} \le {t_2}} \right]\kern-0.15em\right] = \left[\kern-0.15em\left[ {{t_1}} \right]\kern-0.15em\right] \le \left[\kern-0.15em\left[ {{t_2}} \right]\kern-0.15em\right]$, 即tr(t₁(ρ))≤tr(t₂(ρ));

·ρ⊭⊥_Q, ρ⊨γ₁→_Qγ₂当且仅当ρ⊭γ₁或者ρ⊨γ₂.

若ρ⊨γ, 则称ρ可满足γ.Exogenous量子算子逻辑L_E能够刻画用密度算子描述的开放量子系统.例如:任意给定量子密度算子ρ∈D(H_qB), 设量子算子公式$\gamma : = T_A^{qB} \le \frac{1}{2}I,$若有ρ⊨γ, 则语义解释为$tr(T_A^{qB}(\rho )) \le \frac{1}{2}$, 它表示投影测量结果m(m是使得命题公式(∧A)_qB为真的赋值)的概率小于等于$\frac{1}{2}$.在第2.3节, 将用该逻辑描述开放的量子马尔可夫链.

Exogenous量子算子逻辑L_E的推理规则包括两条:(1) α₁, α₁→_Cα₂⊢α₂; (2) γ₁, γ₁→_Qγ₂⊢γ₂.

作为公理化系统, Exogenous量子算子逻辑L_E具有可靠性和完备性.由于篇幅原因, 另文给予证明.

定理1. Exogenous量子算子逻辑L_E是可靠且完备的.

给定量子密度算子ρ∈D(H_qB), 对于量子算子公式(闭式)γ的可满足检测算法的复杂度分析如下:

设|qB|=n, 密度算子用2ⁿ×2ⁿ矩阵表示, 矩阵的相加减的复杂度是O(2ⁿ×2ⁿ), 矩阵的乘法复杂度是O(2³ⁿ), 量子算子公式的长度为|γ|.解释量子算子公式γ中的项$ [\kern-0.15em[ \int \alpha ]\kern-0.15em] = \sum\limits_{v \in |\alpha |} {tr(} P{}_v(\rho ))$的复杂度为O(2³ⁿ), 解释项$\left[\kern-0.15em\left[ {{t_1} \otimes {t_2}} \right]\kern-0.15em\right] = tr(({t_1} \otimes {t_2})\rho )$的复杂度为O(2⁴ⁿ), 解释项$ [\kern-0.15em[ T_A^G ]\kern-0.15em] = tr(T_A^G(\rho ))$的复杂度为O(2⁴ⁿ), 解释项$\left[\kern-0.15em\left[ {{t_1} + {t_2}} \right]\kern-0.15em\right]$的复杂度为O(2²ⁿ).

综上所述, 检测量子算子公式γ的可满足性需要的复杂度为O(2⁴ⁿ|γ|).

定理2.给定量子密度算子ρ∈D(H_qB)、量子算子公式γ, 检测ρ可满足γ(ρ⊨γ)的时间复杂度为O(2⁴ⁿ|γ|).

2.3 基于L_E的量子马尔可夫链

为了应用L_E描述开放量子系统, 首先, 先建立一类量子马尔可夫链:

$\langle S,HqB,\varepsilon \rangle .$

与文献[3]相比, 这里S⊆D(H_qB), |S|=m为有限状态集, 量子算子ε:D(H_qB)→D(H_qB).

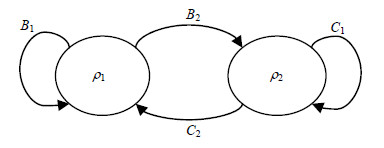
在实际应用中, 利用该量子马尔可夫链模型能够描述一类开放量子系统, 比如开放量子行走^[16].考虑二点图上的开放量子行走, S={ρ₁, ρ₂}, 量子态之间转移如图 1, 其中, ${B_1}B_1^{\rm{†}} + {B_2}B_2^{\rm{†}} = I,{C_1}C_1^{\rm{†}} + {C_2}C_2^{\rm{†}} = I$.

Baltazar等人基于Exogenous量子命题逻辑建立了量子计算树逻辑, 构造有限量子Kripke结构刻画了逻辑语义, 但它只适合于描述封闭量子系统^[18].为了刻画开放量子系统的量子态属性, 下面定义基于Exogenous量子算子逻辑的量子马尔可夫链.

定义1. Exogenous量子马尔可夫链是五元组M= < S, H_qB, ε, l_init, 2^AP, L > , 其中,

(1) ε是H_qB上的量子运算;

(2) l_init⊆H_qB是量子初态的Hilbert子空间;

(3) L:S→2^AP称为标签函数, 其中, AP⊆qAtom, |AP|=n, S⊆D(H_qB), |S|=m.

任意ρ∈S, supp(ρ)表示为ρ的非零特征值对应的特征向量生成的本征空间.设ρ, ρ'∈S, 若supp(ρ')⊆supp(ε(ρ)), 则称ρ可达ρ', 记号为ρ→ρ'.定义从量子初态ρ₀∈l_init出发的一条无穷路径为π=ρ₀→ρ₁→…, 所有从ρ₀出发的无穷路径记为Paths(ρ₀).π[i]=ρ_i表示路径π的第i个量子态; π[i..]=ρ_iρ_i+1…表示从ρ_i出发的一条无穷路径; π[..i]=ρ₀ρ₁…ρ_i表示从ρ₀出发到ρ_i的一条有穷路径.

文献[9]定义的量子马尔可夫链是 < H_qB, ε > , 将它扩展为 < H_qB, ε, l_init, 2^AP, L > , 其中, AP={qb₁, qb₂, …, qb_n}.该模型与Exogenous量子马尔可夫链 < S, H_qB, ε, l_init, 2^AP, L > 相比, 模型形式是相近的, 但是前一个模型中AP是经典原子命题集, 刻画的是量子态经典属性; 后一个模型AP是量子算子原子命题集, 它利用Exogenous量子算子逻辑刻画量子态的量子属性.与文献[17]构造的量子Kripke结构T= < S, R > 相比, 两个都是用来描述有限量子态的量子属性, 但一个是针对封闭量子系统, 另一个是针对开放量子系统.

3 可达性分析 3.1 常用可达性

在经典模型检测中, 属性的检测一般归结为验证状态可达性; 对于量子模型检测, 验证量子状态是否可达对量子属性的检测也是有意义的.常见可达性公式有下一步可达(next)、最终可达(future)、一致可达(global)、无限经常可达(infinitely often)、最终永远可达(ultimately forever).关于Exogenous量子马尔可夫链, 重点提出下列4种常用可达性:

(1)最终可达:π⊨Fγ当且仅当∃i≥0, π[i]⊨γ;

(2)一致可达:π⊨Gγ当且仅当∀i≥0, π[i]⊨γ;

(3)最终永远可达:π⊨Uγ当且仅当∃i≥0, ∀j≥i, π[j]⊨γ;

(4)无限经常可达:π⊨Iγ当且仅当∀i≥0, ∃j≥i, π[j]⊨γ.

定义2.给定一个Exogenous量子马尔可夫链M, ρ₀∈l_init, Δ={F, G, U, I}, γ是一个Exogenous量子算子公式, 定义M, ρ₀⊨Δγ当且仅当对于任意的π∈Paths(ρ₀), 有π⊨Δγ.

例1:给定一个Exogenous量子马尔可夫链:M= < S, H_qB, ε, l_init, 2^AP, L > , 其中,

·量子运算$\varepsilon = \sum\limits_{i = 1}^5 {{E_i} \cdot E_i^† } $, 运算元E_i(i=1, 2, …, 5)分别为

$\begin{array}{l} {E_1} = \frac{1}{{\sqrt 2 }}(|1\rangle \langle 0 + 1| + |3\rangle \langle 2 + 3|),\\ {E_2} = \frac{1}{{\sqrt 2 }}(|1\rangle \langle 0 - 1| + |3\rangle \langle 2 - 3|),\\ {E_3} = \frac{1}{{\sqrt 2 }}(|0\rangle \langle 0 + 1| + |2\rangle \langle 2 + 3|),\\ {E_4} = \frac{1}{{\sqrt 2 }}(|0\rangle \langle 0 - 1| + |2\rangle \langle 2 - 3|),\\ {E_5} = \frac{1}{{10}}(|0\rangle \langle 4| + |1\rangle \langle 4| + |2\rangle \langle 4| + 4|3\rangle \langle 4| + 9|4\rangle \langle 4|), \end{array}$

其中, 式子$|0 \pm 1\rangle = \frac{1}{{\sqrt 2 }}(|0\rangle \pm |1\rangle ),|2 \pm 3\rangle = \frac{1}{{\sqrt 2 }}(|2\rangle \pm |3\rangle )$.

·S={εⁿ(|ϕ > < ϕ|)|n∈N, |ϕ > < ϕ|∈l_init};

·AP={t≤t}为量子算子原子命题集, t的论域是有界线性算子B(H_qB);

·L:S→2^AP;

·l_init=span{|0 > , |1 > }∪span{|2 > , |3 > }.

下面讨论几种量子属性的可达性.

(1)给定量子算子公式${\gamma _1}: = T_{\{ 0,1\} }^{\{ 0,1,2,3,4\} } = I$, 语义解释为:投影测量结果属于{0, 1}的概率等于1.取ρ₀=|0 > < 0|∈l_init, Gγ₁表示对于从初始状态ρ₀出发的每条路径的每一个可达量子态, 量子算子公式γ₁都是可满足的, 即, 投影测量结果属于{0, 1}.注意到:对于任意n∈N, 均有${\varepsilon ^n}(|0\rangle \langle 0|) = \frac{1}{2}(|0\rangle \langle 0| + |1\rangle \langle 1|)$, 因而有M, ρ₀⊨Gγ₁成立.

(2)给定量子算子公式${\gamma _2}: = aI \le T_{\{ 1,2,3,4\} }^{\{ 0,1,2,3,4\} },$其中, a为任意小的非零正数, 语义解释为:投影测量结果属于{1, 2, 3, 4}的概率大于等于a.设一组投影算子P₀={|0 > < 0|}, P₁=I-P₀.取ρ₀=|0 > < 0|∈l_init, F¬_Qγ₂表示对于从初始状态ρ₀出发的每条路径存在着一个可达量子状态, 量子算子公式γ₂是不可满足的.由于$\mathop {\lim }\limits_{k \to + \infty } {({P_1} \cdot \varepsilon )^k}({\rho _0}) = 0$, 所以一定存在一个可达量子状态ρ₁使得ρ₁⊨¬_Qγ₂, 所以有M, ρ₀⊨¬_Qγ₂成立.该结论也说明了量子态|0 > < 0|为吸收态^[9].

(3)给定量子算子公式${\gamma _3}: = T_{\{ 3\} }^{\{ 0,1,2,3,4\} } = \frac{1}{2}I$, 语义解释为:投影测量结果为3的概率等于$\frac{1}{2}$.

取${\rho _0} = \frac{1}{2}(|3\rangle \langle 3| + |4\rangle \langle 4|) \in l{}_{init}$, Iγ₃表示对于从初始状态ρ₀出发的每条路径的每一个可达量子态, 量子算子公式γ₃是无限经常可达(可满足).由于对于任意ρ∈span{|3 > , |4 > }, ∀n∈N均有${\varepsilon ^n}(\rho ) = \frac{1}{2}(|3\rangle \langle 3| + |4\rangle \langle 4|)$, 所以投影测量结果3是以一定概率无限经常可达的, 因而有M, ρ₀⊨Iγ₃.

(4) (续(3)), 对于任意ρ₀∈l_init, 可推导出M, ρ₀⊨¬_QUγ₃.

在定义2中, 称ρ为Δγ的一个可满足解, 所有可满足解记为Sat_M(Δγ).对于4种可达性公式的可满足解算法分析如下.

3.2 可满足性

4种可达性公式的可满足集记为Sat_M(Δγ)={ρ∈S|M, ρ₀⊨Δγ}, 具体分析如下:

(1) Sat_M(Fγ)={ρ∈S|∃n∈N, supp(εⁿ(ρ))∩S∩Sat_M(γ)≠0};

(2) Sat_M(Gγ)=S\Sat_M(F¬γ);

(3) Sat_M(Uγ)=Fixpoint{λx.{supp((ε^-1(X))∩S}∪X, Sat_M(γ)}, 其中, ε^-1(X)={ρ∈S|ε(ρ)⊆X};

(4) Sat_M(Iγ)=S\Sat_M(U¬γ).

可达性检测算法的复杂度计算分为两个过程:首先是Exogenous量子马尔可夫链的检测算法, 如果将量子原子命题替换为经典原子命题, 利用经典检测算法^{[7, 18]}, 求出算法的复杂度为O(|γ||S|²); 其次是Exogenous量子算子公式的检测算法, 根据定理2可知算法的复杂度为O(2⁴ⁿ|γ|), 所以计算出可达性公式Δγ的可满足性检测算法复杂度如下:

定理3.给定一个Exogenous量子马尔可夫链M, ρ∈l_init, , Δγ的可满足性检测算法复杂度为O(|γ|²|S|²2⁴ⁿ).

3.3 可判定性

文献[19, 20]表明了给定一个马尔可夫链, 判定是否存在一个正整数n使得经过n步从起始状态达到目标状态的概率为有理数r是一个Skolem问题.所谓Skolem问题是指给定一个方阵M, 是否存在一个正整数n使得(Mⁿ)_ij=0.Skolem问题属于数论可判定性问题, 是一个公开未解决的问题.Exogenous量子马尔可夫链作为马尔可夫链的量子意义下的推广, 也存在可判定性问题.

给定一个Exogenous量子马尔可夫链M, ρ₀∈l_init, ,一个量子算子公式γ, M, ρ₀⊨Δγ是否是可判定的, 下面对此进行分析.

命题1.设V=Sat_M(γ)={ρ∈S|ρ⊨γ}, Z={n∈N|εⁿ(ρ)∈V}, 给定4种可达性公式Δγ, Δ={F, G, U, I}, 有:

(1)若最终可达Fγ是可判定的当且仅当判定Z是非空的;

(2)若一致可达Gγ是可判定的当且仅当判定Z是自然数集;

(3)若最终永远可达Uγ是可判定的当且仅当判定Z是无穷多;

(4)若无限经常可达Iγ是可判定的当且仅当判定Z是去除有限多个自然数外的无穷多个.

命题1表明, 对可达性公式Δγ的判定可以转化为一类正整数集合Z的属性判定.

定义3^{[21, 22]}.给定一个m阶方阵A, 一个向量x∈Q^m和一个子空间V⊆Q^m, 判定是否存在一个非负整数n使得Aⁿx∈V, 称这类问题为高阶轨道问题.

命题2.关于Z={n∈N|εⁿ(ρ)∈V}的判定是一个高阶轨道问题.

记Z={n∈N|εⁿ(ρ)∈V}的判定问题为DProblem.若εⁿ(ρ)∈V, 则有${P_{{V^ \bot }}}{\varepsilon ^n}(\rho ) = O$, 因而有$tr({P_{{V^ \bot }}}{\varepsilon ^n}(\rho )) = 0$.这样, 对DProblem判定等价于对集合$Z = \{ n \in N|tr({P_{{V^ \bot }}}{\varepsilon ^n}(\rho )) = 0\} $的属性判定.由于ε是开放量子系统的一个量子运算, U是作用在复合量子系统ρ⊗|0 > < 0|(不妨设环境处于量子态|0 > )的酉运算, 则${\varepsilon ^n}(\rho ) = T{r_{env}}({U^n}(\rho \otimes |0\rangle \langle 0|){({U^† })^n})$, 因而, 对DProblem的判定又可以转化为对集合$Z = \{ n \in N|tr({P_{{V^ \bot }}}T{r_{env}}({U^n}(\rho \otimes |0\rangle \langle 0|){({U^† })^n})) = 0\} $的属性判定.若给定一个系综{p_i, ρ_i}, 密度算子ρ表示为$\sum {_i{p_i}{\rho _i}} $, 其中, ρ_i=|ϕ_i > < ϕ_i|, 则DProblem的判定又可转化为对Z={n∈N|Uⁿ|ϕ_i > |0 > ∈V⊗|0 > , ∀i}的属性判定.根据命题2, DProblem为一类高阶轨道问题.

高阶轨道问题由Kannan和Lipton提出, 该问题与Skolem问题紧密相关^[23], 关于它的判定是一个公开性问题.相关工作已经证明:当V是一维的, 高阶轨道问题有多项式时间算法; 当V是二维和三维的, 高阶轨道问题属于NP^RP[19].

4 广义量子Loop程序终止问题

假设有一个含有n个量子系统qb₁, qb₂, …, qb_n的量子寄存器, 并且对于每个i≤n, qb_i的状态空间是${H_{q{b_i}}},$ε是Hilbert空间H_qB上的一个量子运算, $\tilde M = \sum\nolimits_m {m{P_m}} $是H_qB上可观测量.对于任意的$X \subseteq spec(\tilde M)$(谱分解), 广义量子Loop程序(记为GQLoop)由ε, $\tilde M$和X定义为

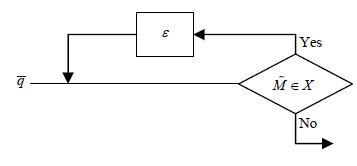
${\rm{while }}(\tilde M[\bar q] \in X)\{ \bar q: = \varepsilon (\bar q)\} ,$

其中, $\bar q$表示qb₁, qb₂, …, qb_n.设${M_1} = {M_X} = \sum\nolimits_{m \in X} {{M_m}} $并且${M_0} = {M_{\bar X}} = I - {M_X} = \sum\nolimits_{m \in spec(M) - X} {{M_m}} $, 其中, I是恒等算子, 控制部分$\tilde M[\bar q] \in X$或M∈X表示为投影测量算子M_X, ${M_{\bar X}}$在$\bar q$上的作用.广义量子Loop程序的工作方式和计算过程如图 2和图 3所示, 其中, $\rho _{in}^{(n)}$为输入态, $\rho _{mid}^{(n)},p_{NT}^{(n)}(\rho )$分别表示不终止的量子态和概率, $\rho _{out}^{(n)},p_T^{(n)}(\rho )$分别表示终止的量子态和概率.

给定输入态$\rho _{in}^{(0)}$和广义量子Loop程序, 如果对于某一个正整数n, 有$p_{NT}^{(n)}(\rho _{in}^{(0)}) = 0,$则称广义量子Loop程序在输入态$\rho _{in}^{(0)}$上是终止的.

广义量子Loop程序是一个量子马尔可夫链 < H_qB, ε, l_init, 2^AP, L > .若取AP={t≤t}, t的论域是有界线性算子B(H_qB), 同时, 量子状态集为有限, 则广义量子Loop程序也是一个Exogenous量子马尔可夫链.控制部分M∈X用量子算子公式表示为$\gamma \equiv (O \le T_X^{qB}){ \wedge _Q}(T_X^{qB} \le I)$, 其中, $T_X^{qB}$为一个投影算子项.量子算子公式γ的语义解释如下:

对于任意给定一个输入态$\rho _{in}^{(n)},\rho _{in}^{(n)}| = \gamma $, 当且仅当$\rho _{in}^{(n)}| = (O \le T_X^{qB})$且$\rho _{in}^{(n)}| = (T_X^{qB} \le I)$, 也就是:

$0 \le tr(T_X^{qB}(\rho _{in}^{(n)})) \le 1.$

从语义角度分析, $T_X^{qB}$是广义量子Loop程序中的投影算子M₁, 意味着$p_{NT}^{(n)}(\rho _{in}^{(0)}) = tr(T_X^{qB}(\rho _{in}^{(n)})).$

终止问题是(广义)量子Loop程序的一个重要研究对象^[24], 对于广义量子Loop程序的终止问题, 它可以用可达性公式来表示.

命题3.任意给定输入态$\rho _{in}^{(0)}$, 若存在正整数n, 使得$p_{NT}^n(\rho _{in}^{(0)}) = 0$, 即广义量子Loop程序经过n步计算后在输入态$\rho _{in}^{(0)}$上是终止的, 当且仅当存在一个Exogenous量子马尔可夫链M, 使得$M,\rho _{in}^{(0)}| = F\gamma $, 其中,

$\gamma : = T_X^{qB} = O.$

在命题中, $M,\rho _{in}^{(0)}| = F\gamma $意味着:对于任意$\pi \in Paths(\rho _{in}^{(0)})$, 有π⊨Fγ, 则存在一个正整数n, 使得$\pi [n] = \rho _{in}^{(n)}| = \gamma $, 其语义解释为$tr(T_X^{qB}(\rho _{in}^{(n)})) = 0$, 所以$p_{NT}^n(\rho _{in}^{(0)}) = 0$, 即, 在输入态$\rho _{in}^{(0)}$上是终止的.因而, 广义量子Loop程序终止对应了Exogenous量子马尔可夫链中量子算子公式$T_X^{qB} = O$是最终可达的.

命题3表明了广义量子Loop程序终止问题可以归结为Exogenous量子马尔可夫链的最终可达性Fγ, 因而, 验证广义量子Loop程序的终止问题等价于检测Fγ的可满足性.

5 结束语

量子马尔可夫链作为量子世界有噪声环境下的数学模型, 有着广泛的理论和实际的应用价值, 对量子马尔可夫链的研究是有意义的.在量子信息论中, 量子通信信道是一类量子马尔可夫链; 在量子程序语言中, 量子Loop程序是以量子马尔可夫链为数学模型.文中构造了Exogenous量子算子逻辑, 它用来刻画开放量子系统.与毕克霍夫-冯·诺依曼量子逻辑相比, 数学结构更为简单.在建立Exogenous量子马尔可夫链基础上, 利用量子算子逻辑刻画量子马尔可夫链的量子态属性.与已有工作相比, 该模型能够描述量子态的量子属性, 可以应用于量子属性的模型检测.可达性是模型检测的关键性问题, 文中定义了4种常用可达性, 给出了它们的可满足检测算法和计算复杂度, 并且分析了它们的判定性问题.作为应用, 分析了广义量子Loop程序是一个Exogenous量子马尔可夫链, 将程序终止问题与可达性问题联系在一起.

致谢 在此, 我们向对本文的工作给予支持和建议的同行、同学和老师表示感谢.