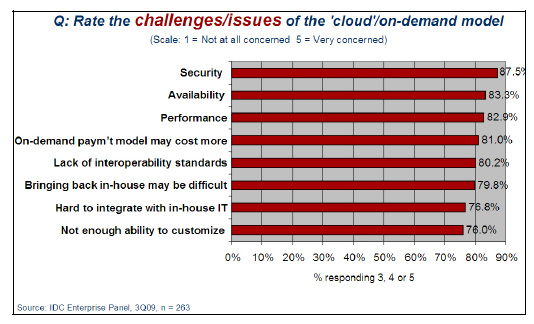
云计算是一种基于互联网的计算, 通过远程服务器集群为企业或个人用户共享数据、集中存储、在线资源服务等[1, 2]. 云模型的重要组成部分是资源池和基于虚拟化的服务, 其面向用户(cloud client)的基本服务模型一般包括软件即服务(software as a service, 简称SaaS)、平台即服务(platform as a service, 简称PaaS)和基础设施即服务(infrastructure as a service, 简称IaaS). 云存储(cloud storage)是虚拟化存储服务的一种具体体现, 被称为数据存储即服务(data storage as a service, 简称DaaS), 支持异构云 数据存储接口, 允许用户或应用程序提供资源池服务[3]. 整体来看, 云数据存储在逻辑存储池中, 在物理上由若干远程存储服务器集群通过虚拟化池的形式来支持, 其云存储容量可扩展, 通过存储服务提供. 云存储提供商负责保障数据的可访问性和可用性、物理环境的保护与运行. 企业或个人用户通过购买、租赁存储空间来存储数据. 价格低廉、部署方便, 云用户随着云应用的增长而爆炸式增长;多租户高效共享实现了服务成本下降和可扩展性提高. 但在应用过程中, 只有二成的用户愿意将私有数据进行云存储;超过半数用户愿意用云存储进行备份、归档及灾难备份等. 云存储中的数据活跃性并不高, 大都为静态数据或非活跃数据[4]. 这表明, 用户对云存储的安全需求越来越强烈. 根据Gartner的调查报告[5] (如图 1所示), 安全性成为当前云计算中最重要的挑战.
|
Fig. 1 Challenges during the development of cloud computing 图 1 云计算发展中面临的挑战 |
企业或个人用户在使用云存储的过程中, 因缺乏数据私密性、安全性机制保障, 数据泄露事件频发, 如SaaS服务提供商Salesforce. com遭受攻击导致大量租户隐私泄露(2007年), CSDN网站600多万用户信息被黑客盗取(2011年)等. Verizon发布的2014年度数据泄露调查报告对各类攻击、泄露事件进行了总结, 并对企业用户、个人用户提出了相关防护建议[6], 文献[1, 7]系统总结了云计算安全的相关问题.
由于云用户并没有对数据的绝对控制权, 在客观上, 要求云存储系统能够保障数据的完整性、可用性、机密性[8]. 云存储中, 对数据的分布存储一般分成6种:
· 第1种, 非分布策略(non-distribution), 即原始数据仅存储在一个节点中. 该方法具有典型的单点失效 问题.
· 第2种, 副本策略(replication), 即原始数据的完整备份分布在多个节点中. 如, RAID采用的就是这种冗余策略. 该方法在一定程度上避免了单点失效, 任意一个节点都可以提供原始数据.
· 第3种, 分片策略(splitting), 即原始数据切分成n份并存入n个不同节点中. 较大程度地提高了数据的机密性, 但存在典型的拜占庭失效问题, 任意一个节点失效都将导致数据无法恢复.
· 第4种, 纠删码切割策略(erasure codes). 如文献[9, 10], 将原始数据切割成k份, 通过系列编码形成n(n>k)个文件块并存入n个节点中, 只需从n个节点中选择k个可用文件块, 即可重构原始文件. 该方法极大地提高了云存储的可靠性, 但编码复杂, 计算量较大.
· 第5种, 信息分散策略(information dispersal), 是提高云存储可用性、可靠性以及机密性的一种有效方式. 其基本思路来源于Robin所提出的IDA算法[11], 本质上是一种(k, n)门限机制. 将文件分成n份子文件, 分发至n个不同的存储节点, 并确保任意k(k<n)份子文件的数据可充分重构原始文件, 如文献[12, 13].
· 第6种, 秘密共享策略(secret sharing, 简称SS), 是机密信息分布存储的一种有效方式, 如文献[14-16]等. 其思想与IDA一样属于(k, n)门限机制, 与IDA不同的是, IDA的每个分片都包含了可被敌手理解的部分原始数据信息;而SS的每个分片(影子)与原始秘密具有相同形式却彼此互异, 且不透露任何原始秘密信息. 但是SS耗费大量存储成本, 不适合对常规大文件、备份文件做云存储.
这6种数据存储方法中, 前3种主要针对数据的冗余保护;后3种增加了数据机密保护能力, 其中, SS最适合机密数据的分布式存储.
从目前的云安全架构来看[17, 18], 云存储体系结构在逻辑上一般可分为存储层、基础管理层、应用接口层和访问层, 密码学在接口层、访问层为租户提供数据管理及安全保护功能. 目前, 对称密码、非对称密码等经典密码算法主要被用于静态数据、业务数据的访问控制[19-22], 但加密后的数据并未充分考虑如何防止数据丢失、破坏、篡改等恶意行为, 尤其对于机密数据而言, 一旦发生上述恶意行为, 加密后的机密数据丢失或备份被破坏, 都将严重后果. 针对密码等机密数据的分布存储, 现有方案大都基于Shamir的多项式门限密码进行安全存储, 如文献[9, 14, 23, 24], 极大地提高了数据的机密性, 但是, 一旦影子数据被恶意篡改、恶意云节点提供伪影子, 则无法恢复原始秘密, 而当多个云存储节点中的影子被恶意获取并达到门限数, 敌手则可以通过恶意共谋形式恢复原始秘密. 继Shamir之后, 所提出的若干可验证的门限秘密共享方案[25-31]引入认证、签名等方式对抗恶意共谋, 这类方案本身也可以应用于云存储, 但在部署上将带来额外负担. 本文的目的是结合云存储容器及云租户的特征信息, 在我们以往工作基础上构建一种适合云机密数据存储的门限秘密共享方案, 与云存储本身紧密耦合, 除了分发与恢复的基本计算外, 不会带来额外开销, 且云服务器本身不需要对方案进行密钥管理. 针对机密数据保护及当前所存在的问题, 本文假设敌手模型为:攻击者已具备获取云存储数据的能力, 具备修改数据的最高权限, 且在多云模式下, 敌手可以合作共谋. 在此基础上, 本文基于云存储介质特征展开适合云存储机密数据保护的秘密共享方案研究. 本文所做方案的主要贡献如下:
(1) 提出了一种新的面向云存储的门限秘密共享方案, 利用云租户与云存储容器的唯一标识特征信息构造多维球面, 通过证明多维球面原理下球面坐标对原始秘密的可恢复性, 设计了保护云租户机密数据的(k, n)门限秘密分发与恢复算法, 提高云存储的可靠性.
(2) 设计了伪数据验证、防御恶意恢复等安全校验机制, 在敌手控制云存储环境下, 所做秘密共享方案具备对抗能力, 增强了原始秘密恢复的完整性保障.
(3) 所提出的方案门限值及校验坐标由云租户管理, 云存储系统仅负责对影子坐标的分布存储, 减少了云存储系统对方案的密钥管理成本, 提高了可用性;同时, 实现了门限值k的动态性, 提高了密钥空间, 增强了机密性.
(4) 本文所提出的方案可作为云存储中机密数据保护的一个参考方案, 同时, 所提出的多维球面秘密共享方案也可应用于具有唯一标识特征的分布式网络的安全存储、秘密保护.
本文第1节介绍相关工作. 第2节主要简述本文思路, 同时对后续内容涉及到的基本概念进行约定. 第3节介绍所提方案的秘密共享过程, 重点阐述算法原理. 第4节对多维球面重构思路进行证明, 阐述秘密恢复过程. 第5节对所提模型进行性能分析、比较和仿真. 最后, 第6节进行总结和展望.
1 相关工作云存储使个人和企业用户的存储与共享业务变得便捷, 但在安全管理、秘密管理等方面有众多问题需要解决, 引发了学术界和工业界的广泛研究, 在云存储的数据安全性, 尤其是机密性保障方面涌现出了众多研究成果, 本节对这些相关工作进行阐述.
在多租户环境下, 密码学是数据机密性保护的首选工具. Microsoft提出的Cryptographic Cloud Storage[32]为云存储中建立虚拟私有存储服务(virtual private storage service)、基于对称密码、非对称密码进行数据保护提供了参考依据. CloudProof[33], Cryptonite[34]以及CloudSeal[14]基于对称密钥算法建立了数据机密性机制. DepSky[23]是一种云上云(cloud of clouds)的云存储系统, 设计了DepSky-CA认证协议, 基于1 024位的非对称密钥RSA算法实现签名, 利用SHA-1进行摘要哈希, 同时, 也使用了AES进行对数据进行加密, 并将加密数据与共享密钥进行编码后分发在4个云上, 每个云上都存储数据块和共享密钥. Intercloud[24]和NCloud[35]使用对称密钥方式进行数据保护, 同时还将加密后的数据分布式存储在多重云(multi-clouds)上, 每个云上存储部分加密后的数据, 提高了数据机密程度.
对于密钥等机密数据的安全保护, 是云存储中一大挑战[36]. 分布式门限秘密共享方案是云存储中机密数据保护的一种有效方法. 门限秘密共享概念是1979年由Shamir[37]和Blakley[38]分别提出的. 其基本思想是:将秘密分割成n个秘密分片, 分发给n个参与者, 任意k(k为门限值, 且k≤n)个或者多于k个参与者协同合作就可以恢复秘密, 而少于k个则无法恢复. 这两个方案具有里程碑意义, 但参与者提供虚假的秘密份额将可能导致秘密无法恢复[39]. 在后来的研究中, 如文献[25-31]等秘密共享方案中, 提出了防御欺骗的若干解决方法. 这些方法为提高分布式数据存储的可靠性提供了新的思路, 研究者们利用分布式秘密共享方案展开了云存储研究. 文献[40]提出的KLMS密钥管理系统设计了秘密共享、公私钥共享、唯一秘密、唯一私钥这4种不同的部署模型, 对密钥实施严格的按需访问控制. 文献[9]提出的存储系统中, 基于Shamir秘密共享机制将密钥分布式存储到密码服务器中. Intercloud[24]使用秘密共享方案和多重来分发加密数据影子数据和密钥, 对数据进行对称加密后, 基于秘密共享机制将密钥拆分成影子密钥, 并将这些影子附加在数据片上进行分发. CloudSeal[14]集成了对称加密、基于代理的重加密以及秘密共享方案对用户进行云访问控制. DepSky[23]中使用Shamir秘密共享方案对机密数据进行分布式保护. MCDB[41]方案中, 提出基于Shamir秘密分发算法确保多云存储的数据安全. 文献[15]借鉴Shamir的思路, 利用多项式拉格朗日插值法, 结合密文关键字搜索算法, 设计了一个秘密共享来防御恶意共谋攻击. 但其方法是通过增强影子的互异复杂性来增加共谋者发现影子秘密的难度, 并未从本质上解决如本文所提出的共谋敌手攻击问题. CloudStash[16]利用Shamir秘密共享方法设计了云存储数据保护方案, 但无法避免共谋问题.
本文在以上研究者的思路基础上, 考虑结合云存储介质本身的特征, 提出对云存储中的机密数据进行分布式秘密共享. 在前期工作中[29], 我们于2013年6月提出了基于三维球面原理的(4, n)分布式秘密共享模型, 具有较高的运算效率. 但其门限值固定为4, 在密钥空间及保密性能上不具有可扩展性. 2014年10月, 该方案被俄罗斯从事密码分析的科研人员Chervyakov等4人宣告破解[42], 他们利用三维球面下门限值k恒等于4这一漏洞, 在一台四核Intel Core i7计算环境下, 通过内存探测进行参数调整, 在7.5小时内, 对256位和512位的秘密信息分别进行了破解恢复(该项工作被写入俄罗斯State Task#8581框架的基础部分). 本文在综合分析前期工作基础上, 利用多维球面(n-Sphere)原理, 将秘密数据转换为多维球面的球心, 经过多次球心迁移及坐标变换, 将云存储容器特征标识映射到多维球面空间, 通过设计算法, 对秘密数据进行影子分发, 存储到n个存储容器中;在恢复阶段, 选取任意k个云存储容器(k≥4) , 对机密数据进行恢复. 同时, 设计影子数据可验证机制和防篡改机制对抗共谋敌手模型, 加强分布式秘密共享机制的可用性和安全性.
2 约定及基本思路当前, 云存储模型支持现有的标准存储协议, 如用于块存储的iSCSI、用于文件网络存储的CIFS/NFS或WebDAV等, 为兼顾通用性, 本文方案不考虑存储协议、存储介质、存储网络的差异. 有如下约定:
(1) 分发者:任一个人用户或企业用户都可以作为秘密共享的分发者, 分发者具有唯一标识ID0, 该标识是对分发者唯一特征(如UserID&Password组合值)进行安全哈希(如SHA)后产生的整数串. 本文所用哈希算法为SHA-512, 但仍标记为SHA.
(2) 参与者:云存储系统(无论是单个云还是多重云)中的每个存储容器都为秘密共享的参与者, 每个参与者拥有唯一整数串标识ID, 用IDSet={ID0, ID1, …, IDn}记为n个云存储容器集合.
(3) 秘密:秘密S0是分发者委托云进行存储的机密信息, 用二进制表示.
在以上约定的基础上, 秘密分发是指分发者将秘密S0转换成影子秘密后分发给参与者进行存储的过程, 要求每个影子秘密互不相同, 同时与原始秘密具有形式上的相似性. 秘密恢复是指在n个参与者中获得任选k个参与者所存储的影子秘密后, 恢复原始秘密的过程.
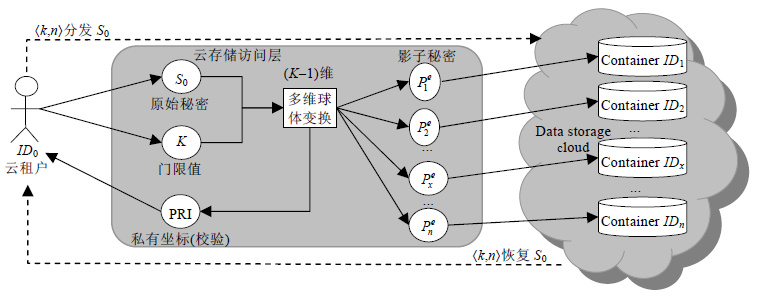
本文利用多维球面数学原理完成秘密分发与恢复过程. 一个m维的多维球体是普通球体在m维空间的衍生. 在欧几里得空间里, 一般用m维坐标及半径r来表示m维球体上的点. 在特殊情况下, 一维球体是一个线段, 二维球体是一个圆盘, 三维球体就是常见的普通球体. 本文所述球体为大于等于三维的多维球体, 球心及球面坐标一般用$\langle $x1, x2, …, xm$\rangle $形式表示. 方案基本框架如图 2所示.
|
Fig. 2 Framework of the proposed scheme 图 2 本文方案框架 |
首先, 将秘密S0转化为m维(m≥3, m=K-1) 坐标形式, 并经过位置迁移变换生成m维球面球心坐标P0, 使得球心与秘密坐标有一个空间距离;然后, 将n个云存储容器作为方案的参与者, 并将其ID信息转换为m维坐标形式, 设计映射规则, 将n个参与者坐标映射到以P0为球心的m维球面上, 生成n个影子秘密坐标, 并将这n个影子秘密坐标分发到n个参与者(云存储容器)中, 完成秘密分发过程. 在秘密恢复阶段, 论证任意k个线性不相关向量的m维坐标决定球心的唯一性, 从n个参与者中任取k个(k=m+1) 坐标向量线性不相关的坐标点, 并根据规则映射、迁移逆运算及分发者验证信息恢复出原始球心P0, 然后设计转换算法, 得出原始秘密S0. 在该过程中, 设计算法保证影子秘密的可验证性, 同时防御恶意窃取者的非法恢复.
3 秘密分发算法设计 3.1 秘密S0转换为球心为了将原始秘密S0转换为球心, 首先需要将原始秘密、分发者ID、参与者ID转换为m维坐标形式, 在此基础上, 按照多维球面原理设计算法将秘密信息S0最终转换为m维球体的球心P0:$\langle $c1, c2, …, cm$\rangle $.
(1) 初始化S0到m维坐标的转换算法
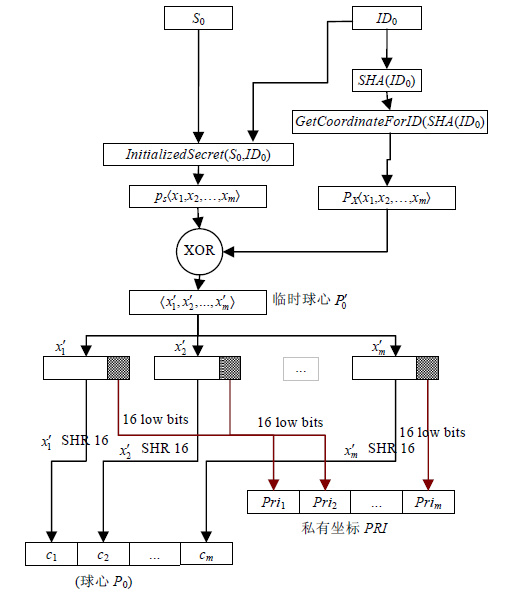
原始秘密到m维坐标的转换算法设计如图 3所示. 从存储结构来说, 信息在计算机中的存储形式是二进制序列, 故本文将所有涉及到的信息都按照二进制方式进行计算处理. 为了将秘密信息S0最终转换为m维球体的球心P0:$\langle $c1, c2, …, cm$\rangle $, 需设计秘密信息初始化为m维坐标形式的算法. 如图 4所示, 首先将S0与ID0进行按位异或, 二进制信息按平均分割原则划分为(m-1) 份, 作为前m-1维坐标值$\langle $x1, x2, …, xm-1$\rangle $(若S0长度不能被m整除, 则不够整除的秘密部分作为xm-1的值). 最后, 将S0的哈希值与分发者ID0的哈希值的异或结果作为第m维坐标xm的值.

|
Fig. 3 Processes to initialize original secret to coordinate Ps 图 3 原始秘密初始化为坐标Ps |
|
Fig. 4 Processes to generate sphere center point from original secret 图 4 原始秘密转化为球心的过程 |
算法中, 第m维坐标为校验值, 由原始秘密及分发者ID计算形成, 用于恢复阶段校验前m-1维信息的正确性. 算法1为算法伪代码, 在函数命名上沿用了我们前期工作[29]的名称结构.
算法 1. Program InitializedSecret(S0, ID0).
(1) Stemp=S0 XOR ID0; //原始秘密隐藏
(2) L=length(Stemp);
(3) xBit=[L/(m-1) ]; //前m-1维每维坐标的位数, 向上取整;
(4) For i=1 to (m-2) //前m-2维坐标值
(5) xi=S0 SHR(L-xBitxi); //取第i个xBit长度
(6) EndFor
(7) xm-1=Stemp AND (2L-(m-2) xxBit-1) ; //剩余部分生成第m-1维
(8) xm=SHA(S0) XOR SHA(ID0); //最后一维用于校验
(9) Return Ps$\langle $x1, x2, …, xm$\rangle $ //转换后的坐标形式
End
(2) ID信息到m维坐标的转换算法
分发者和参与者的ID信息同样用二进制形式表示, 采用平均分割形式, 将ID信息分割成m份, 若ID信息不能被m整除, 则不足部分作为第m维坐标信息. 具体描述如算法2所示.
算法 2. Program GetCoordinateForID(ID).
(1) L=length(ID); PX=$\langle $x1, x2, …, xm$\rangle $
(2) xBit=[L/m];
(3) For i=1 to m-1 //前m-1维
(4) xi=S0 SHR(L-xBitxi);
(5) Endfor
(6) xm=ID AND (2L-(m-1) xxBit-1) ; //剩下的部分生成第m维
(7) Return PX$\langle $x1, x2, …, xm$\rangle $
End
结合分发者ID0信息, 利用算法1、算法2将原始秘密转换成m维球心坐标, 算法设计如图 4所示.
在该算法中, 在转换为球心坐标的过程中, 利用分发者ID0信息对原始秘密S0进行了两阶段的隐藏和保护. 第1阶段是将S0和ID0信息按位异或后进行坐标初始化(算法1) ;第2阶段是将初始化的坐标信息与ID0哈希后生成的坐标信息进行按位异或, 对坐标信息进行二次隐藏保护, 生成临时球心坐标P′0. 在此基础上, 取临时球心每一维坐标的后16位, 生成分发者私有坐标PRI(用于恢复阶段), 剩余部分形成球心坐标P0. 算法伪代码如算法3所示.
算法 3. Program GetSphereCenter(S0, ID0).
(1) 定义球心P0, 临时球心P′0私有坐标PRI;
(2) IDtemp=SHA(ID0); //隐藏分发者信息
(3) Ps$\langle $x1, x2, …, xm$\rangle $=InitializedSecret(S0, ID0);
(4) Pid0$\langle $x1, x2, …, xm$\rangle $=GetCoordinateForID(IDtemp);
(5) For i=1 to m
(6)
(7) PRI. xi=
(8) P0. ci=
(9) EndFor
(10) 获得P0:$\langle $c1, c2, …, cm$\rangle $; //球心坐标
(11) 获得PRI$\langle $x1, x2, …, xm$\rangle $ //分发者私有坐标
END
3.2 参与者ID信息映射到同一多维球面为了将参与者ID信息全部转换为m维坐标. 首先将IDSet中的参与者ID信息与分发者ID0的哈希值异或操作, 以便在坐标信息中隐藏参与者信息. 之后基于算法2, 生成所有参与者的坐标信息, 即
| $I{{D}_{i}}=I{{D}_{i}}XORSHA\left( I{{D}_{0}} \right),$ |
| ${{P}_{i}}=\left\langle p{{x}_{1}},p{{x}_{2}},\ldots ,p{{x}_{m}} \right\rangle =GetCoordinateForID\left( I{{D}_{i}} \right),$ |
定义CSet={P1, P2, … , Pn}为所有参与者坐标集合.
IDSet中, 存储中单位容器的ID信息互不相同, 在m维欧几里得空间中, 所有Pi与球心P0之间的空间距离长短不一. 为了将所有参与者信息映射到以P0为球心的同一多维球面上, 需将所有半径都统一为某长度R(半径). 值得一提的是, 半径R的信息不能透露出原始ID信息, 否则, 一旦某个Pi与P0的欧氏距离恰好等于R, 则给原始秘密带来风险. 因此, 本文选取CSet中离P0最远的坐标点作为基准, 并在该基准上进行一个随机微量延长(e), 生成多维球体半径R , 使得所有参与者坐标都需要进行有限延长才能映射到球面上. 用ri表示参与者坐标Pi到球心P0=$\langle $c1, c2, …, cm$\rangle $的欧式距离, 则
| ${{r}_{i}}=\sqrt{\sum\limits_{i=1}^{n}{{{({{x}_{i}}-{{c}_{i}})}^{2}}}}$ | (1) |
| $R=\underset{i=1}{\overset{n}{\mathop{Max}}}\,({{r}_{i}})+\varepsilon $ | (2) |
在延长之前, 所有参与者坐标都在以P0为球心、R为半径的m维球面内部;将CSet的点通过半径延长方式投影到多维球面上之后, 以三维球面为例, 图 5中, P1, P2, P3分别投影到球面上的P′1, P′2, P′3.

|
Fig. 5 Demonstration of constructing participants onto sphere surface 图 5 将参与者坐标投影到球面 |
下面讨论CSet={P1, P2, … , Pn}中的点P投影到以P0为球心、R为半径的m维球面上后, 延伸到球面上的点(记为
利用几何投影的方法, 将延伸后的点分别投影到坐标系的每一维度中, 延伸后的点的每一维的坐标值就等于该点在相应维度的投影的长度. 记R与ri的比值为θi:
| ${{q}_{i}}=R/{{r}_{i}}$ | (3) |
则延长点
| $P_{i}^{e}.{{x}_{j}}={{\theta }_{i}}\cdot ({{P}_{i}}.{{x}_{j}}-{{c}_{j}})+{{c}_{j}}$ | (4) |
所以, 参与者IDi所生成的坐标Pi$\langle $x1, x2, …, xm$\rangle $经投影后形成球面坐标
| $P_{i}^{e}=\langle {{\theta }_{i}}({{P}_{i}}.{{x}_{1}}-{{c}_{1}})+{{c}_{1}},...,{{\theta }_{i}}({{P}_{i}}.{{x}_{m}}-{{c}_{m}})+{{c}_{m}}\rangle $ | (5) |
记shadowSet=
按照上述算法, 基于多维球面原理, 分发者利用ID0以及IDSet参与者信息, 将原始秘密S0转换成影子秘密shadowSet=
算法 4. Program ShareSecret(S0, ID0).
(1) P0=$\langle $c1, c2, …, cm$\rangle $=GetSphereCenter(S0, ID0); //球心
(2) IDSet={ID1, ID2, …, IDn}
(3) For i=1 to n //生成参与者坐标
(4) IDi=IDi XOR SHA(ID0);
(5) Pi=GetCoordinateForID(IDi);
(6)
(7) EndFor
(8) R=Max(ri)+e;
(9) For i=1 to n //生成影子秘密
(10) θi=R/ri;
(11)
(12) EndFor
(13) For i=1 to n //存入云存储容器
(14) Container(IDi). store(
(15) EndFor
END
按照算法4, 分发者将原始秘密共享到云存储器中. 可以看出, 从解密的角度来说, 密钥由3部分组成, 即, 分发者ID0、K以及私有坐标PRI. 这些信息由云用户本身留存, 云存储服务器不做额外管理(零密钥管理). 下面将讨论如何从云存储器中恢复出原始秘密.
4 (k, n)秘密恢复过程在(k, n)门限秘密共享方案中, 门限秘密恢复的过程就是在获得k个影子秘密份额后, 对秘密的完整恢复过程. 本文方案就是获取任意k(k=m+1) 个球面上的坐标点求出球心坐标, 进而恢复出原始秘密S0的过程. 因此, 首先需要证明k个球面坐标点决定一个唯一球体.
4.1 球体唯一性求解原理定理 1. 任意K个线性不相关的m维坐标确定唯一球心.
在本文的前期工作[29]中, 证明了三维球面坐标下, 任意不共面的4个点确定唯一球心. 本节将对m维球面(m≥3) 上任意k(k=m+1) 个m维坐标点能确定唯一球体的充分条件进行证明, 以支撑m维球面模型下的门限可恢复性. 下面将对m维球面模型的门限可恢复性进行分析, 证明得出至 少m+1个点可以唯一确定一个m维球面方程, 少于m+1个点将无法得出唯一确定的m维球面方程. 即, 求解给定CSet={P1, P2, … , Pn}中的任意k个点能确定唯一球心P0$\langle $c1, c2, …, cm$\rangle $的充分条件.
假设半径为r, 则任意点Pl=$\langle $x1, x2, …, xm$\rangle $的轨迹方程为
| $\sum\limits_{i=1}^{m}{{{({{P}_{l}}.{{x}_{i}}-{{P}_{0}}.{{c}_{i}})}^{2}}}={{r}^{2}}.$ |
在CSet中任取k个点, 为方便描述, 记k个点分别为P1, P2, … , Pk, 则
| $\left\{ \begin{array}{*{35}{l}} \sum\limits_{i=1}^{m}{{{({{P}_{1}}.{{x}_{i}}-{{P}_{0}}.{{c}_{i}})}^{2}}}={{r}^{2}} \\ \sum\limits_{i=1}^{m}{{{({{P}_{2}}.{{x}_{i}}-{{P}_{0}}.{{c}_{i}})}^{2}}}={{r}^{2}} \\ ... \\ \sum\limits_{i=1}^{m}{{{({{P}_{k}}.{{x}_{i}}-{{P}_{0}}.{{c}_{i}})}^{2}}}={{r}^{2}} \\ \end{array} \right.$ | (6) |
整理成未知数c1, c2, … , cm的方程得:
| $\left\{ \begin{array}{*{35}{l}} {{c}_{1}}({{p}_{2}}.{{x}_{1}}-{{p}_{1}}.{{x}_{1}})+{{c}_{2}}({{p}_{2}}.{{x}_{2}}-{{p}_{1}}.{{x}_{2}})+...+{{c}_{m}}({{p}_{2}}.{{x}_{m}}-{{p}_{1}}.{{x}_{m}})=\frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{2}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ {{c}_{1}}({{p}_{3}}.{{x}_{1}}-{{p}_{1}}.{{x}_{1}})+{{c}_{2}}({{p}_{3}}.{{x}_{2}}-{{p}_{1}}.{{x}_{2}})+...+{{c}_{m}}({{p}_{3}}.{{x}_{m}}-{{p}_{1}}.{{x}_{m}})=\frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{3}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ ... \\ {{c}_{1}}({{p}_{k}}.{{x}_{1}}-{{p}_{1}}.{{x}_{1}})+{{c}_{2}}({{p}_{k}}.{{x}_{2}}-{{p}_{1}}.{{x}_{2}})+...+{{c}_{m}}({{p}_{k}}.{{x}_{m}}-{{p}_{1}}.{{x}_{m}})=\frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{m}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ \end{array} \right.,$ |
简记为
| $\left[ \begin{matrix} {{p}_{2}}-{{p}_{1}} \\ {{p}_{3}}-{{p}_{1}} \\ ... \\ {{p}_{k}}-{{p}_{1}} \\ \end{matrix} \right]\left[ \begin{matrix} {{c}_{1}} \\ {{c}_{2}} \\ ... \\ {{c}_{m}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{2}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{3}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ ... \\ \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{k}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ \end{matrix} \right]$ | (7) |
显然, 按照矩阵乘法运算的基本条件, 有k=m+1. 将方程化为“AX=B”的矩阵方程组形式, 系数行列式A为一个mxm的矩阵:
| $\det (A)=\left[ \begin{matrix} {{p}_{2}}-{{p}_{1}} \\ {{p}_{3}}-{{p}_{1}} \\ ... \\ {{p}_{k}}-{{p}_{1}} \\ \end{matrix} \right]$ | (8) |
常数项B为
| $B=\left[ \begin{matrix} \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{2}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{3}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ ... \\ \frac{1}{2}\left( \sum\limits_{i=1}^{m}{({{p}_{k}}.x_{i}^{2})}-\sum\limits_{i=1}^{m}{({{p}_{1}}.x_{i}^{2})} \right) \\ \end{matrix} \right]=\left[ \begin{matrix} {{b}_{1}} \\ {{b}_{2}} \\ ... \\ {{b}_{m}} \\ \end{matrix} \right]$ | (9) |
根据Cramer规则, 公式(7) 有唯一解的条件是当且仅当|A|≠0, 即矩阵A的秩rank(A)=m. 故可得出结论:任取k(k=m+1) 个坐标线性不相关的m维坐标可确定唯一球心, 且球心$\langle $c1, c2, …, cm $\rangle $中第i维坐标ci的解为
| ${{c}_{i}}=\frac{\det ({{A}_{i}})}{\det (A)}$ | (10) |
其中, Ai是把A中第i列元素对应地换成常数项B, 而其余各列保持不变所得到的行列式.
4.2 通过逆运算恢复原始秘密根据上一节数学原理可以计算得到球心P0, 接下来根据算法3及算法1的逆运算恢复出原始秘密信息S0, 分成3个阶段, 其中, 第1阶段按照算法3逆运算, 利用球心P0(由定理1获得)、分发者本身的ID0以及分发者持有的私有坐标PRI恢复出秘密坐标Ps;第2阶段由秘密坐标恢复出经算法1变换后的秘密Stemp;第3阶段为验证阶段, 利用前m-1维坐标形成的Stemp, 和第m维坐标进行秘密验证, 若验证通过, 则恢复出原始秘密. 具体如算法5所示.
算法 5. Program GetSecretFromCenter(ID0, PRI, P0).
(1) IDtemp=SHA(ID0);
(2)
(3) For i=1 to m //第1阶段恢复Ps
(4) P′0. xi=PRI. xi OR (P0. ci SHL 16) ;
(5) Ps. xi=
(6) EndFor
(7) Stemp=Ps. x1;
(8) For i=2 to m-1 //第2阶段恢复临时秘密Stemp
(9) Stemp=(Stemp SHL (length(Ps. xi))) OR Ps. xi;
(10) EndFor
(11) Verify=SHA(ID0) XOR SHA(Stemp); //第3阶段校验
(12) If (Verify <> Ps. xm) Then
(13) return "Error Secret";
(14) EndIf
(15) S0=Stemp XOR ID0; //恢复秘密
(16) return S0
END
5 性能分析本节将首先从方案分析所提出的面向云存储的秘密共享方案的有效性;然后, 从假数据攻击、合谋攻击两个方面讨论所提出的方案的可验证性和主动防御性能;最后, 从算法运算、通信代价的角度展开性能分析, 并对所提方案进行秘密分发和恢复的实验仿真.
5.1 有效性分析本文所提出的方案使用多维球面原理进行秘密分发和恢复, 秘密经过转化成为k-1维球体的球心坐标, 并将参与者容器ID信息映射为以秘密坐标为球心、以R为半径的球面, 映射后的参与者坐标作为影子坐标分发到n个参与者容器中. 在恢复过程中, 获取任意k个线性不相关的影子坐标, 按照线性方程组的方式恢复出球心坐标, 进而通过逆运算恢复原始秘密, 其门限值k具备动态性, 且满足算法的分发和恢复条件. 从云存储的实际运算角度来说, 云租户将原始秘密以分发者身份通过所提出的方案存储到n个云存储容器中, 运算过程由云计算中间件来完成. 此外, 本文所提出的方案充分利用分发者、云存储容器、秘密本身的特征构建存储与恢复策略, 云租户仅需要在客户端存储一个用于校验的私有坐标即可恢复数据, 不需要专门的密钥管理机制. 因此, 从算法设计及应用具有较强的可用性.
5.2 假数据攻击分析门限秘密共享方案中, 秘密恢复阶段中参与者提供虚假影子秘密的行为称为假数据攻击. 按照本文开始部分所做敌手假设, 在秘密恢复过程中, 攻击者若对影子秘密进行恶意篡改, 并在恢复阶段给云租户提供一份篡改后的影子秘密, 那么秘密分发者将无法恢复出正确的秘密.
本文所提出的方案设计了针对假数据攻击的验证过程. 假设某些云存储容器的数据被攻击者恶意篡改, 或云存储容器被攻击者控制, 只对外提供虚假信息, 则这类容器在作为参与者参与秘密恢复计算时, 被认为是假数据提供者. 设f为篡改行为的形式化函数, 一旦云存储容器IDx所存储影子秘密
任取k线性不相关的影子秘密, 假设其中至少有1个影子秘密
| $\begin{matrix} [P_{x1}^{e}...,f(P_{xx}^{e}),...,P_{xk}^{e}]\Rightarrow {{P}_{0}}:\langle {{c}_{1}},{{c}_{2}},..,{{c}_{m}}\rangle , \\ [I{{D}_{0}},{{P}_{0}},PRI]\Rightarrow {{P}_{s}}:\langle {{x}_{1}},...,{{x}_{m-1}},{{x}_{m}}\rangle , \\ \langle \underline{{{P}_{s}}.{{x}_{1}},{{P}_{s}}.{{x}_{2}},...,{{P}_{s}}.{{x}_{m-1}}}\rangle \ \text{XOR}\ I{{D}_{0}}\Rightarrow {{S}_{temp}}. \\ \end{matrix}$ |
Ps的第m维坐标为验证位, 在正常情况下, 该值等于分发者ID0与Stemp的哈希抑或值, 即
| $\underline{{{P}_{s}}.{{x}_{m}}}=SHA(I{{D}_{0}})\ \text{XOR}\ SHA({{S}_{temp}}).$ |
受污染的影子秘密
按照本文的敌手模型, 在门限秘密共享方案中, 攻击者有可能通过获得云存储容器中足够的影子秘密来恢复原始秘密. 攻击者利用某种途径攻陷云存储容器, 收集k份影子秘密, 或多个攻击者合谋获取k份影子秘密, 达到秘密共享方案的门限值, 试图按算法恢复原始秘密. 本方案对这种攻击进行了防御设计, 攻击者在拥有k份合法的影子秘密份额时, 通过秘密恢复算法恢复出球心坐标后, 并不能得知秘密.
要完整恢复出原始秘密, 需要用到分发者ID0、门限值k、分发者私有坐标PRI. 从某种意义上讲, (ID0, k, PRI)是本文方案的密钥组. 事实上, 影子秘密数据的存储并不是以坐标形式存储, 而是以二进制等长(如512位)形式存储, 只有结合k值后才能清晰表达出影子秘密坐标. 因此, 从k值角度来看, 攻击者只有穷举法可以进行探测. 攻击者在探测到个k值时, 为恶意恢复, 则需要从n个云存储容器中获取k份影子秘密数据. 假设该k份影子秘密线性不相关, 根据定理1可恢复出球心P0. 接下来的恢复过程需要私有坐标PRI以及分发者ID0信息, 即
| $\begin{matrix} \left. \begin{align} & [1]\ (P_{1}^{e},P_{2}^{e},...,P_{k}^{e})\Rightarrow {{P}_{0}}:\langle {{c}_{1}},{{c}_{2}},..,{{c}_{m}}\rangle \\ & \underline{[2]\ PRI私有坐标} \\ & \underline{[3]\ k值} \\ \end{align} \right\}\Rightarrow 临时球心{{{{P}'}}_{\text{0}}}, \\ {{{{P}'}}_{\text{0}}}\ \text{XOR}\ \underline{SHA(I{{D}_{0}})}\Rightarrow 秘密坐标{{P}_{s}}, \\ {{P}_{s}},I{{D}_{0}}\Rightarrow 原始秘密. \\ \end{matrix}$ |
攻击者获得球心坐标后, 若没有获得私有坐标PRI以及ID0, 则球心坐标为无效信息, 无法恢复出原始秘密. 显然, 猜测分发者所持有的私有坐标(m个16位)、猜测分发者ID0的SHA哈希信息(512位)在实际应用上是不现实的事情. 当然, 若攻击者同时获得了私有坐标和ID0的信息, 就相当于云租户自己丢失了密钥, 不属于本节的讨论范畴.
5.4 运算及通信性能比较本方案计算量主要体现为下列3种形式:计算摘要信息、进行比特操作以及计算矩阵所需要的计算量. 记SHA-512运算所需计算量为Ca, 矩阵计算所需计算量为Cm. 比较过程中忽略比特运算的计算时间. 在描述过程中, 记A1~A5分别表示算法1~算法5;T1表示定理1. 表 1对计算量、通信量进行了统计.
| Table 1 Statistics of computation and communication 表 1 计算量、通信量统计 |
在本方案运行过程中, 共需要经历初始化、秘密分发、秘密恢复过程这3个阶段. 在秘密共享过程中, 需要经历A1~A4. 在秘密恢复过程中, 需要进行矩阵计算. 在秘密初始化阶段中, A1需要两次摘要计算, 因此, 计算量为2xCa. A2涉及到的计算量均为比特操作. A3需要3次摘要计算, 计算量为3xCa. A4为分发过程, 调用了A2, A3, 并进行了n个SHA操作, 计算量则为A3+nxA2+nxCa. 在秘密恢复过程中, T1需要计算m维坐标值, 共O(kxCm)的计算量, A5的计算量则为T1+A2+3xCa.
本节对分发和恢复过程中的云存储调度进行分析, 用“通信量”指标进行描述. 按照算法分析, A4, T1, A5的通信量级为O(n). 考虑到方案中有来自攻击者的攻击行为, 这样就需要重新进行k次通信以恢复秘密. 假设被攻击的概率为prob[0,1]), 那么出现攻击行为后, T1, A5的通信量为k(1+prob).
从表 1的统计结果来看, 较大的计算量集中在矩阵计算和SHA哈希摘要计算, 计算量级、通信量级最大为O(n), 从云计算的角度来讲, 计算量级并不大, 是合理的.
在得到本方案的性能统计后, 与其他方案进行对比. 本节选取了与本文所提出的方案一样具有可验证和共谋防御性质的Herzberg[28], Harn[30]和Tang[31]的方案进行对比. 具体性能参数见表 2. 记Harn方案中的横幂运算(ab mod n)的运算量为Ce, 在计算量的对比上, 本文方案中的矩阵计算只涉及到平方和加减运算, SHA摘要计算Ca和矩阵计算Cm的复杂度都要低于横幂计算的复杂度. 相对而言, 本文所提出的算法所需运算量较少, 有计算量优势. 在通信量对比上来看, 秘密分发阶段所需的通信量最少;而秘密恢复阶段, 由于受到攻击的概率较小, 故可以忽略. 因此, 在秘密恢复阶段通信量也具有优势.
| Table 2 Comparision of computation complexity and communication amounts 表 2 运算量及通信量性能对比 |
5.5 仿真性能分析
本节将对所提方案进行分发和恢复的性能仿真. 选择Eucalyptus 3.5作为云存储资源仿真工具, 并虚拟化 1 000 000条资源目录作为参与者. 具体仿真配置见表 3.
| Table 3 Simulation parameters 表 3 仿真参数 |
(1) 云存储:秘密分发性能仿真
首先对所提方案的云存储功能进行性能仿真, 主要考察表 3配置环境下, 通过秘密分发的云存储时间性能. 图 6是秘密分发的云存储仿真结果.

|
Fig. 6 秘密分发的云存储性能 图 6 Performance of cloud storage during secret distribution |
从结果可以看出:随着K值的不断增大, 所需存储时间不断增加. 尤其注意到, 当K在100以内时, 存储时间处于毫秒级, 表明所提出方案的存储性能是高效的. 但是也注意到, 仿真结果中有陡增现象, 如K在800左右时间陡增较为剧烈, 主要与仿真过程中云存储容器调度的中间件调动时间相关.
(2) 恢复:秘密重构性能仿真
接下来对所提方案的数据恢复进行仿真, 主要考察从云存储容器中进行秘密重构的时间性能. 图 7是该仿真的结果. 可以看出:随着K值的不断增加, 重构时间不断增加. 锯齿状性能曲线中, 有部分陡增现象, 这主要是因为重构过程中矩阵计算有可能遇到非满秩的病态矩阵, 重新选择合适容器的影子秘密需要时间成本. 因为重构算法需要进行球心的线性方程组求解(矩阵计算), 并需要判断是否具有唯一解的条件. 从总体上来看, 恢复过程所需的时间要远大于分发过程所需要的时间.

|
Fig. 7 Performance of cloud storage during secret reconstruction 图 7 秘密重构的云存储性能 |
6 结论与展望
云存储部署方便、价格低廉, 向用户提供“数据存储即服务(DaaS)”, 个人或企业用户能够高效地实现资源共享、降低成本并提高可扩展性. 然而, 云用户缺乏对数据的绝对控制权, 数据安全, 尤其是机密数据的安全, 成为一大隐患, 也是当前云存储中私有数据存储业务较低的根本原因之一. 因此, 本文提出了一种保护机密数据的分布式安全云存储机制, 利用用户特征、云存储容器特征, 基于多维球面原理, 设计了一种分布式(K, n)门限秘密共享方案. 用户将原始秘密转换m维球体的球心, 结合云存储容器ID信息, 进而转换成n个m维球面坐标, 形成n个影子秘密信息, 并将这些影子秘密作为机密数据分布式存储在n个云存储容器中. 同样, 云用户通过在n个存储容器中选取k(k=m+1) 个m维球面坐标, 在线性方程组系数矩阵为满秩的情况下恢复出球心坐标, 进而恢复出原始秘密信息. 在分发和恢复过程中, 本文设计了面向假数据攻击、共谋攻击的验证方法, 同时, 本文所提出的方案不需要云服务器专门存储密钥, 解密密钥信息由云租户本身掌握, 其密钥信息由分发者标识ID0、分发者持有的私有坐标PRI以及门限值K组成, 这一特征加强了用户对云数据的控制能力. 算法性能分析和真实验分析结果表明, 本文所提出的方案是正确且有效的.
该方案在秘密重构过程中, 所选取影子秘密坐标在算法逻辑上仍然存在k个m维坐标线性相关的情况, 我们当前的解决方案是在重新选取1个影子秘密替换k中的任意一个坐标进行系数矩阵满秩的判断. 因此在下一步的工作中, 我们将进一步就如何确保秘密重构过程中系数矩阵满秩进行深入研究. 同时, 当前方案主要面向云租户私有业务的小文件“短”机密数据, 如何将方案扩展到公有业务的大文件“长”普通数据的存储, 并且保证其存储性能, 也将是后续研究的重点.
致谢 谨在此对评审专家的辛勤工作、客观点评以及在论文陈述方式上给予的中肯建议表示感激.| [1] | Lin C, Su WB, Meng K, Liu Q, Liu WD. Cloud computing security:Architecture, mechanism and modeling. Chinese Journal of Computers, 2013, 36 (9) :1765–1784(in Chinese with English abstract). [doi:10.3724/SP.J.1016.2013.01765] |
| [2] | Tan S, Jia Y, Han WH. Research and development of provable data integrity in cloud storage. Chinese Journal of Computers, 2014, 37 (32) :1–16(in Chinese with English abstract). [doi:10.3724/SP.J.1016.2015.00164] |
| [3] | SNIA. Cloud data management interface (CDMITM). Version 1.1.0, 2014. http://www.snia.org/cdmi |
| [4] | EMC (twinstrata). 2014. http://www.twinstrata.com/ |
| [5] | http://blogs.idc.com/ie/?p=730 |
| [6] | Data breach investigations report. 2014. http://www.verizonenterprise.com/ |
| [7] | Subashini S, Kavitha V. A survey on security issues in service delivery models of cloud computing. Journal of Network and Computer Applications, 2011, 34 (1) :1–11. [doi:10.1016/j.jnca.2010.07.006] |
| [8] | Tse DWK, Chen DQ, Liu QS, Wang F, Wei ZY. Emerging issues in cloud storage security:Encryption, key management, data redundancy, trust mechanism. In:Proc. of the Int'l Conf. of Multidisciplinary Social Networks Research (MISNC 2014). CCIS 473, Springer-Verlag, 2014. 297-310.[doi:10.1007/978-3-662-45071-0_24] |
| [9] | Lin H, Tzeng W. A secure erasure code-based cloud storage system with secure data forwarding. IEEE Trans. on Parallel and Distributed Systems, 2012, 23 (6) :995–1003. [doi:10.1109/TPDS.2011.252] |
| [10] | Abu-Libdeh H, Princehouse L, Weatherspoon H. RACS:A case for cloud storage diversity. In:Proc. of the 1st ACM Symp. on Cloud Computing (SoCC 2010). ACM Press, 2010. 1-12.[doi:10.1145/1807128.1807165] |
| [11] | Rabin MO. Efficient dispersal of information for security, load balancing, and fault tolerance. Journal of the ACM, 1989, 36 (2) :335–348. [doi:10.1145/62044.62050] |
| [12] | Bowers KD, Juels A, Oprea A. HAIL:A high-availability and integrity layer for cloud storage. In:Proc. of the 16th ACM Conf. on Computer and Communications Security (CCS 2009). ACM Press, 2009. 187-198.[doi:10.1145/1653662.1653686] |
| [13] | Resch JK, Plank JS. AONT-RS:Blending security and performance in dispersed storage systems. In:Proc. of the 9th USENIX Conf. on File and Storage Technologies (FAST 2011). San Jose, 2011. 191-202. http://static.usenix.org/legacy/events/fast11/tech/full_papers/Resch.pdf |
| [14] | Xiong H, Zhang X, Yao D, Wu X, Wen Y. Towards end-to-end secure content storage and delivery with public cloud. In:Proc. of the 2nd ACM Conf. on Data and Application Security and Privacy. ACM Press, 2012. 257-266.[doi:10.1145/2133601.2133633] |
| [15] | Kikuchi H, Itoh K, Ushida M, Yamaoka Y, Oikawa T. Secret sharing scheme with efficient keyword search for cloud storage. In:Proc. of the 9th Asia Joint Conf. on Information Security. IEEE Press, 2014. 164-169.[doi:10.1109/AsiaJCIS.2014.33] |
| [16] | Alsolami F, Boult T. CloudStash:Using secret-sharing scheme to secure data, not keys, in multi-clouds. In:Proc. of the 11th Int'l Conf. on Information Technology:New Generations (ITNG 2014). IEEE Press, 2014. 315-320.[doi:10.1109/ITNG.2014.119] |
| [17] | Fu YX, Luo SM, Shu JW. Survey of secure cloud storage system and key technologies. Journal of Computer Research and Development, 2013, 50 (1) :136–145(in Chinese with English abstract). |
| [18] | Grossman RL, Gu Y, Sabala M, Zhang WZ. Compute and storage clouds using wide are high performance networks. Future Generation Computer Systems, 2009, 25 (2) :179–183. [doi:10.1016/j.future.2008.07.009] |
| [19] | Cao N, Wang C, Li M, Ren K, Lou W. Privacy-Preserving multi-keyword ranked search over encrypted cloud data. IEEE Trans. on Parallel and Distributed Systems, 2014, 25 (1) :222–233. [doi:10.1109/TPDS.2013.45] |
| [20] | Zhang XY, Liu C, Nepal S, Pandey S, Chen JJ. A privacy leakage upper bound constraint-based approach for cost-effective privacy preserving of intermediate data sets in cloud. IEEE Trans. on Parallel and Distributed Systems, 2013, 24 (6) :1192–1202. [doi:10.1109/TPDS.2012.238] |
| [21] | Roy I, Setty STV, Kilzer A, Shmatikov V, Witchel E. Airavat:Security and privacy for mapreduce. In:Proc. of the 7th USENIX Conf. on Networked Systems Design and Implementation (NSDI 2010). ACM Press, 2010. 20. https://www.usenix.org/legacy/event/nsdi10/tech/full_papers/roy.pdf |
| [22] | Puttaswamy KPN, Kruegel C, Zhao BY. Silverline:Toward data confidentiality in storage-intensive cloud applications. In:Proc. of the 2nd ACM Symp. on Cloud Computing (SoCC 2011). ACM Press, 2011. 1-13.[doi:10.1145/2038916.2038926] |
| [23] | Bessani A, Correia M, Quaresma B, André F, Sousa P. DepSky:Dependable and secure storage in a cloud-of-clouds. In:Proc. of the 6th Conf. on Computer Systems. ACM Press, 2011. 31-46.[doi:10.1145/1966445.1966449] |
| [24] | Cachin C, Haas R, Vukolic M. Dependable storage in the intercloud. IBM Research Report, 2010 . |
| [25] | Chor B, Goldwasser S, Micali S, Awerbuch B. Verifiable secret sharing and achieving simultaneity in the presence of faults. In:Proc. of the Foundations of Computer Science. IEEE, 1985. 383-395.[doi:10.1109/SFCS.1985.64] |
| [26] | Pedersen TP. Non-Interactive and information-theoretic secure verifiable secret sharing. In:Proc. of the Advances in Cryptology-CRYPTO'91. Berlin, Heidelberg:Springer-Verlag, 1992. 129-140.[doi:10.1007/3-540-46766-1_9] |
| [27] | Gennaro R, Rabin MO, Rabin T. Simplified VSS and fast-track multiparty computations with applications to threshold cryptography. In:Proc. of the 17th Annual ACM Symp. on Principles of Distributed Computing. ACM Press, 1998. 101-111. http://www.eecs.harvard.edu/~cat/cs/tlc/papers/grr.pdf |
| [28] | Herzberg A, Jarecki S, Hugo K, Yung M. Proactive secret sharing or:How to cope with perpetual leakage. In:Proc. of the 15th Annual Int'l Cryptology Conf. on Advances in Cryptology. Springer-Verlag, 1998. 339-352.[doi:10.1007/3-540-44750-4_27] |
| [29] | Tan ZH, Yang GM, Cheng W, Wang XW. Distributed secret sharing scheme based on personalized spherical coordinates space. Computer Science and Information Systems, 2013, 10 (3) :1269–1291. [doi:10.2298/CSIS120801048T] |
| [30] | Harn L. Efficient sharing (broadcasting) of multiple secrets. IEEE Proc. of Computers and Digital Techniques, 1995, 142 (3) :237–240. [doi:10.1049/ip-cdt:19951874] |
| [31] | Tang CM, Wu DO, Chronopoulos AT, Raghavendra CS. Efficient multi-party digital signature using adaptive secret sharing for low-power devices in wireless networks. IEEE Trans. on Wireless Communications, 2009, 8 (2) :882–889. [doi:10.1109/TWC.2008.071286] |
| [32] | Kamara S, Lauter K. Cryptographic cloud storage. In:Proc. of the Financial Cryptography and Data Security. LNCS 6054, Springer-Verlag, 2010. 136-149.[doi:10.1007/978-3-642-14992-4_13] |
| [33] | Popa RA, Lorch JR, Molnar D, Wang HJ, Zhuang L. Enabling security in cloud storage SLAs with CloudProof. In:Proc. of the USENIX ATC. ACM Press, 2011. 1-12. http://www.mit.edu/~ralucap/cloudproof.pdf |
| [34] | Kumbhare A, Simmhan Y, Prasanna V. Cryptonite:A secure and performant data repository on public clouds. In:Proc. of the 5th Int'l Conf. on Cloud Computing. IEEE Press, 2012. 510-517.[doi:10.1109/CLOUD.2012.109] |
| [35] | Alsolami F, Chow CE. N-Cloud:Improving performance and security in cloud storage. In:Proc. of IEEE the 14th Int'l Conf. on High Performance Switching and Routing (HPSR). IEEE Press, 2013. 221-222.[doi:10.1109/HPSR.2013.6602319] |
| [36] | Zissis D, Lekkas D. Addressing cloud computing security issues. Future Generation Computer Systems, 2012, 28 (3) :583–592. [doi:10.1016/j.future.2010.12.006] |
| [37] | Shamir A. How to share a secret. Communications of the ACM, 1979, 22 (11) :612–613. [doi:10.1145/359168.359176] |
| [38] | Blakley GR. Safeguarding cryptographic keys. In:Proc. of the National Computer Conf. 1979. 313-317. http://www.computer.org/csdl/proceedings/afips/1979/5087/00/50870313.pdf |
| [39] | Tompa M, Woll H. How to share a secret with cheaters. Journal of Cryptology, 1989, 1 (3) :133–138. [doi:10.1007/BF02252871] |
| [40] | Björkqvist M, Cachin C, Haas R, Hu XY, Kurmus A, Pawlitzek R, Vukolić M. Design and implementation of a key-lifecycle management system. Lecture Notes in Computer Science, 2010, 6052 :160–174. [doi:10.1007/978-3-642-14577-3_14] |
| [41] | AlZain MA, Soh B, Pardede E. MCDB:Using multi-clouds to ensure security in cloud computing. In:Proc. of the 9th Int'l Conf. on Dependable, Autonomic and Secure Computing (DASC 2011). IEEE Press, 2011. 784-791.[doi:10.1109/DASC.2011.133] |
| [42] | Chervyakov NI, Babenko MG, Deryabin MA, Nazarov AS. Cryptanalysis of secret sharing schemes based on spherical spaces. In:Proc. of the 8th Int'l Conf. on Application of Information and Communication Technologies (AICT). IEEE Press, 2014. 1-5.[doi:10.1109/ICAICT.2014.7035900] |
| [1] | 林闯, 苏文博, 孟坤, 刘渠, 刘卫东. 云计算安全:架构、机制与模型评价. 计算机学报, 2013,36 (9) :1765–1784. [doi:10.3724/SP.J.1016.2013.01765] |
| [2] | 谭霜, 贾焰, 韩伟红. 云存储中的数据完整性证明研究及进展. 计算机学报, 2014,37 (32) :1–16. [doi:10.3724/SP.J.1016.2015.00164] |
| [17] | 傅颖勋, 罗圣美, 舒继武. 安全云存储系统与关键技术综述. 计算机研究与发展, 2013,50 (1) :136–145. |
 2016, Vol. 27
2016, Vol. 27


