2. 武汉大学 计算机学院, 湖北 武汉 430072
2. Computer School, Wuhan University, Wuhan 430072, China
克隆选择算法(clonal selection algorithm,简称CSA)是基于生物免疫系统的克隆选择原理,通过构造记忆单元实现全局与局部搜索平衡.它由一个单个最优个体演变为最优解集,体现免疫的多样性,扩大了搜索区域[1].在克隆选择算法中,抗体多样性只是简单地通过新旧抗体的替换来实现的.但是如果根据亲和度选出的抗体基因非常接近,那么所产生的后代相对于双亲也必然比较接近.这样,所期望的改善就比较小,基因模式的单一性不仅减慢了收敛速度,而且可能导致进化停滞,使算法过早地收敛于局部极值点.
在利用马尔可夫链分析克隆选择算法的收敛性时,设包含最优解的状态为j,当种群X(t1)处于某个状态i(i≠j)时,转移概率pij(t1)≤a(a为一个较小的正数),即此时种群X(t1)收敛于状态j的概率较小.如果当t2>t1时均有pij(t2)≤a,那么,t1时刻的种群X(t1)将发生准早熟收敛现象.当t2>t1时,种群X(t2)发生了早熟现象[2].种群收敛现象的外在表现是,种群中的个体所包含的抗体基因型减少,使种群中个体趋于一致.如果种群不是朝着最优解的方向收敛,那么种群将收敛到局部最优解.在传统的克隆选择算法中,由于己经发生了早熟收敛的种群不能通过交叉操作生成新个体,如果仅仅依靠变异的作用产生新的抗体基因,这时将会发生早熟现象.许多研究表明,在某些情况下,交叉能够比变异提供更高水平的基因重组,从而产生多样抗体[3].
传统的克隆选择算法模型虽然比较粗糙,对免疫克隆选择过程中的内在机理研究还不够深入,然而作为一个智能计算研究的新兴领域,一个受生物免疫系统启发、解决实际问题的智能方法,依然受到许多专家和学者的广泛关注.国内外人工免疫学者在算法构造与设计[4]、内在克隆机理[5]、新算子设计[6]、自适应性研究[7]、记忆能力[8]、编码方式[9]以及与其他智能计算方法相结合[10]等方面进行了大量研究,并取得了众多研究成果.由于传统的克隆选择算法提出了一个基于信息熵的简单克隆算子,根据亲和度的排序增加克隆规模,没有对抗体克隆的自适应性和动态过程进行深入研究.因此,本文针对克隆选择算法的动态过程提出一种品质因数概念,并根据其可能存在的早熟收敛现象和缺少交叉操作问题,设计一种高效克隆退火优化算法(efficient clonal annealing optimizing algorithm,简称ECAOA).它结合了模拟退火算法与免疫系统的克隆选择机制,并维持全局搜索和局部搜索的平衡,可以有效提高算法的搜索效率,从而加快算法的收敛速度.
1 ECAOA算法的操作算子模拟退火算法(simulated annealing,简称SA)是源于对热力学中退火过程的模拟,在某一给定初温下,通过缓慢下降温度参数,使算法能够在多项式时间内给出一个近似最优解[11].SA算法首次被Kirkpatric等人引入优化问题的求解,它具有很好的局部搜索能力,但是总体搜索能力较差.克隆选择算法虽然搜索速度较快,但是基因模式的单一性容易过早地收敛于局部极值点,导致局部搜索精度不高.如果将模拟退火机制融入到克隆选择原理中,则将实现克隆选择算法和模拟退火算法的优势互补,充分地平衡算法的局部和全局搜索能力.本文对ECAOA算法的相关操作算子进行如下定义:
定义 1. 设Tk是趋近于0的温度控制序列,则抗体ai的退火选择概率为
| $p({{a}_{i}})=\frac{{{\text{e}}^{\frac{aff({{a}_{i}})}{{{T}_{k}}}}}}{\sum\limits_{i=1}^{n}{{{\text{e}}^{\frac{aff({{a}_{i}})}{{{T}_{k}}}}}}}$ | (1) |
退火选择概率表明抗体ai以概率p(ai)选择进入下一代群体.Tk表示进化到第k代的退火温度,k表示当前的进化代数,${{T}_{k}}={{T}_{k-1}}\times \left( 1-\frac{k}{n} \right)$,n表示最大进化代数.
定义 2. 设抗体ai={φ0,…,φn-1},aj={r0,…,rn-1},k为交叉节点(l<k<n),则对抗体ai和aj执行的交叉操作Tc(ai,aj)的具体操作步骤如下:
Step 1. 产生新抗体${{{a}'}_{i}}$和${{{a}'}_{j}}:$
| ${{T}_{c}}({{a}_{i}},{{a}_{j}})=\left\{ \begin{array}{*{35}{l}} {{{{a}'}}_{i}}=\{{{\varphi }_{0}},...,{{\varphi }_{k}}\in {{a}_{i}},{{r}_{k+1}},...,{{r}_{n-1}}\in {{a}_{j}}\} \\ {{{{a}'}}_{j}}=\{{{\gamma }_{0}},...,{{\gamma }_{k}}\in {{a}_{j}},{{\varphi }_{k+1}},...,{{\varphi }_{n-1}}\in {{a}_{i}}\} \\ \end{array} \right.$ | (2) |
Step 2. 产生一个随机数rc=random(0,1) ,rc∈[0,1].
Step 3. 分别计算父抗体F和子抗体S的亲和度值aff(F)和aff(S).根据模拟退火算法的Metropolis接受准则,如果min{1,exp(aff(S)-aff(F))/Tk}>rc,则接受新的抗体S,F={ai,aj},$S=\{{{{a}'}_{i}},{{{a}'}_{j}}\}$,Tk是第k次退火温度.
定义 3. 设抗体ai={φ0,…,φn-1},k为变异节点(1<k<n),则对抗体ai执行变异操作Tm(ai)的具体操作步骤如下:
Step 1. 产生子抗体${{T}_{m}}({{a}_{i}})={{{a}'}_{i}}=\{{{\varphi }_{0}},...,{{\varphi }_{k-1}},{{{\varphi }'}_{k}},...,{{\varphi }_{n-1}}\},{{{\varphi }'}_{k}}\oplus {{\varphi }_{k-1}}=1.$
Step 2. 产生一个随机数rm=random(0,1) ,rm∈[0,1].
Step 3. 分别计算父抗体ai和子抗体${{{a}'}_{i}}$的亲和度值aff(ai)和$aff({{{a}'}_{i}}).$根据模拟退火算法的Metropolis接受准则,如果$\min \{1,\exp (-(aff({{{a}'}_{i}})-aff({{a}_{i}}))/{{T}_{k}})\}>{{r}_{m}}$,就接受新的抗体${{{a}'}_{i}}$,Tk是第k次退火温度.
定义 4. 设抗体ai,aj∈A(t),ai和aj之间的增强因子为dij∈{0,1},则抗体ai的增强度为
| $Str({{a}_{i}})=\sum\limits_{j=1}^{n}{{{d}_{ij}}},{{d}_{ij}}=\left\{ \begin{array}{*{35}{l}} 1,\text{ }aff({{a}_{i}})\ge aff({{b}_{i}}) \\ 0,\text{ }aff({{a}_{i}})<aff({{b}_{i}}) \\ 0,\text{ }i=j \\ \end{array} \right.$ | (3) |
定义 5. 设抗体ai的退火选择概率为p(ai),增强度为Str(ai),种群A(t)的规模为|A(t)|,则选择因子d(ai)为
| $\delta \left( {{a}_{i}} \right)=p\left( {{a}_{i}} \right)\acute{\ }\left| A\left( t \right) \right|$ | (4) |
定义 6. 设抗体ai的增强度表示为Str(ai),选择因子为d(ai).如果满足下列条件:
Str(a1)+Str(a2)+…+Str(ai-1)<d(ai)<Str(a1)+Str(a2)+…+Str(ai),
则选择操作Ts(A(t))为
| ${{T}_{s}}\left( A\left( t \right) \right)={{a}_{i}}$ | (5) |
定义 7. 设$\overline{aff(*)}$表示种群A(t)的平均亲和度值,aff(ai)表示抗体ai的亲和度值,PopSize表示种群规模,则准
成熟抗体群Abest(t)为
| $\left\{ \begin{array}{*{35}{l}} {{A}_{best}}(t)=\{{{a}_{i}}|aff({{a}_{i}})\ge \overline{aff(*)},{{a}_{i}}\in A(t)\} \\ \overline{aff(*)}=\frac{\sum\limits_{i=1}^{PopSize}{aff({{a}_{i}})}}{PopSize} \\ \end{array} \right.$ | (6) |
定义 8. 抗体距离H(ai,aj):
| $\left\{ \begin{array}{*{35}{l}} {{d}_{ij}}={{a}_{i}}\oplus {{a}_{j}} \\ H({{a}_{i}},{{a}_{j}})=\sum\limits_{k=1}^{L}{{{d}_{ij}}(k)/L} \\ \end{array} \right.$ | (7) |
上述的抗体距离H(ai,aj)采取了归一化处理,L为编码长度,dij(k)为dij的第k位编码,⊕为按位异或运算符.当H(ai,aj)=0时,抗体ai和抗体aj的所有基因相同;当H(a i,aj)=1时,抗体ai和抗体aj的所有基因均不相同,抗体之间差异最大.
定义 9(d领域). 如果抗体ai和抗体aj的距离H(ai,aj)满足:
| $\underset{\delta \to 0}{\mathop{\lim }}\,(H({{a}_{i}},{{a}_{j}})-\delta )=0$ | (8) |
则称d为抗体ai的d领域.
抗体ai的d领域(或称为抗体相似度阈值)反映的是与抗体ai相似的抗体个数情况.我们用mi(d)表示ai的d领域内包含群体A(t)中抗体的个数.下面通过d领域的相关属性,定义抗体的浓度一般性公式.抗体的浓度表示基因相同(或者近似)的抗体在整个抗体种群中所占的比例[12],抗体的浓度定义如下:
定义 10. 抗体浓度C(ai):
| $C({{a}_{i}})=\frac{{{m}_{i}}(\delta )}{PopSize}$ | (9) |
其中,PopSize为当前种群的规模.抗体的浓度用于调节抗体的克隆规模,当某些抗体的亲和度较大时,会被克隆增扩,其浓度会快速上升,从而导致少数几种类型的抗体充斥整个免疫系统.因此,应当采取一定的措施抑制那些浓度较高的抗体[13].抗体的生存度(或称为激励度)反映的是抗体应答抗原和被其他抗体激活的综合能力[14].在免疫应答中,为了维持免疫响应的稳定平衡,具有高亲和度且低浓度的抗体将受到促进,而低亲和度且浓度较高的抗体将受到抑制.通过这种相似细胞之间的抑制作用,抗体种群的多样性得到保持,同时增强了算法的全局搜索能力和多解搜索能力.本文定义抗体ai的生存度函数如下:
定义 11. 抗体生存度S(ai):
| $S\left( {{a}_{i}} \right)=|l\times aff\left( {{a}_{i}} \right)-\beta \times C\left( {{a}_{i}} \right)|$ | (10) |
其中,aff(ai)和C(ai)分别表示抗体ai的亲和度和浓度,l和b为控制参数,S(ai)>0,l+b=1.
定义 12. 设种群A(t)经过克隆、变异、交叉和选择操作后得到的准成熟抗体群为Abest(t),抗体ai的生存度表示为S(ai),则克隆抑制操作Tr(Abest(t))为
| ${{T}_{r}}\left( {{A}_{best}}\left( t \right) \right)=a,S\left( a \right)=max\{S\left( {{a}_{i}} \right),{{a}_{i}}\in {{A}_{best}}\left( t \right)\}$ | (11) |
克隆抑制算子能够有效地抑制浓度高的抗体,促进亲和度高的抗体进入新的抗体种群.
定义 13. 设ECAOA算法的种群为A(t),准成熟抗体群表示为Abest(t),非成熟抗体群表示为$\overline{A(t)}$=A(t)- Abest(t),随机生成的新抗体为b,则种群更新操作${{T}_{d}}(\overline{A(t)})$为
| ${{T}_{d}}(\overline{A(t)})=b$ | (12) |
种群更新算子Td是对种群中亲和度较低的抗体进行更新,从抗体种群中删除这些抗体并以随机生成的新抗体替代,有利于保持抗体的多样性,探索新的可行解空间区域.
2 ECAOA算法的流程定义 14. 假设克隆操作表示为Tk,变异操作表示为Tm,交叉操作表示为Tc,选择操作表示为Ts,克隆抑制操作表示为Tr,种群更新操作表示为Td,则ECAOA算法可以描述为六元组ECAOA=(Tk,Tm,Tc,Ts,Tr,Td).
ECAOA算法的克隆操作Tk采取CSA算法的克隆操作方式.
本文设计的ECAOA算法的具体流程如图 1所示.

|
Fig. 1 Flow chart of ECAOA algorithm 图 1 ECAOA算法的流程图 |
ECAOA算法的执行步骤如下:
Step 1. 随机产生一个初始种群A(t)={ai|i=1,2,…,PopSize},种群的规模|A(t)|=PopSize,并对每个抗体ai进行编码,ai=φ1,…,φn,|ai|=n,初始进化代数t=0,初始退火温度Tt=1.
Step 2. 评估每个抗体的亲和度.
Step 3. 根据CSA算法的克隆操作,对种群A(t)执行克隆操作Tk.
Step 4. 执行变异操作Tm.
Step 5. 执行交叉操作Tc.
Step 6. 执行选择操作Ts,并将选择出来的抗体保留到下一代.
Step 7. 将种群A(t)划分为Abest(t)和$\overline{A(t)}$.
Step 8. 对准成熟抗体群Abest(t)执行克隆抑制操作Tr.
Step 9. 对非成熟抗体群$\overline{A(t)}$执行种群更新操作Td.
Step 10. 令${{T}_{t}}={{T}_{t-1}}\times \left( 1-\frac{t}{PopSize} \right)$,t=t+1.如果Tt≈0,则算法运行结束;否则,跳转到Step 2.
3 ECAOA算法性能的评价指标本文为了更好地对算法的性能进行评估,特对以下一些相关的算法性能评价指标进行定义.
定义 15. 线性性能X(s):
| $X(s)=\frac{1}{t}\sum\limits_{t=1}^{T}{\overline{aff(t)}}$ | (13) |
$\overline{aff(t)}$是在第t时刻的平均亲和度值.算法的线性性能指标表示了算法从开始运行一直到当前为止的时
间段内性能指标的平均值,它反映了算法的动态性能.
定义 16. 离线性能X*(s):
| ${{X}^{*}}(s)=\frac{1}{t}\sum\limits_{t=1}^{T}{af{{f}^{*}}(t)}$ | (14) |
aff*(t)=best{aff(1) ,aff(2) ,…,aff(t)}是在[0,t]时间内亲和度值最大的.X*(s)表示算法在运行过程中最佳性能值的累积平均,反映了算法的收敛性能.
定义 17. 设ECAOA算法的线性性能表示为X(s),离线性能表示为X*(s),则算法的品质因数Q为
| $Q=\frac{2\times X(s)\times {{X}^{*}}(s)}{X(s)+{{X}^{*}}(s)}$ | (15) |
品质因数Q结合了算法的线性性能和离线性能.Q值越高,表明算法的综合性能越优良.
定义 18. 误差性能E(s):
| $E(s)=\frac{1}{t}\sum\limits_{t=1}^{T}{\frac{S(t)-{{S}^{*}}}{{{S}^{*}}}}$ | (16) |
其中,S(t)是算法在第t时刻运行所得的实际优化值,S*为问题的期望最优值.算法的误差性能E(s)指标反映了算法从开始运行一直到当前为止的时间段内对问题的最佳优化程度,其值越小,意味着算法的优化性能越好.
定义 19. 设种群的规模为|A(t)|,50次算法独立运行到指定的迭代数时不同的抗体数之和为Sum,则群体多样性Mu为
| ${{M}_{u}}=\frac{Sum}{50\times |A(t)|}$ | (17) |
为了从理论上更好地分析ECAOA算法的收敛性能,本文首先引入波雷尔-坎特里(Borel-Cantelli)引理 和Markov链的相关基本理论.
引理 1(波雷尔-坎特里(Borel-Cantelli)引理 ) [15]. 设A1,A2,…,Ak,…,An是概率空间上的一事件序列,令Pk=P{Ak}.若$\sum\limits_{k=1}^{\infty }{{{P}_{k}}<\infty },$则
| $P\left\{ \underset{n=1}{\overset{\infty }{\mathop{\cap }}}\,\underset{k\ge n}{\mathop{\cup }}\,{{A}_{k}} \right\}=0$ | (18) |
若$\sum\limits_{k=1}^{\infty }{{{P}_{k}}=\infty },$且各Ak相互独立,则
| $P\left\{ \underset{n=1}{\overset{\infty }{\mathop{\cap }}}\,\underset{k\ge n}{\mathop{\cup }}\,{{A}_{k}} \right\}=1$ | (19) |
算法的收敛是指当算法迭代足够多的次数以后,群体中包含全局最佳个体的概率近于1.根据波雷尔-坎特里引理 和文献[16],本文引入对算法收敛性的具体定义:
定义 20[16]. 设{Xn|n≥0}概率空间上定义的随机序列,若存在随机变数S*,使
| $P\{\underset{n\to \infty }{\mathop{\lim }}\,({{X}_{n}}={{S}^{*}})\}=1$ | (20) |
或者对于∀ε>0,有:
| $P\left\{ \underset{n=1}{\overset{\infty }{\mathop{\cap }}}\,\underset{k\ge n}{\mathop{\cup }}\,[|{{X}_{n}}-{{S}^{*}}|\ge \varepsilon ] \right\}=0$ | (21) |
则称随机序列{Xn|n≥0}以概率为1收敛于随机变数S*.
在ECAOA算法中,初始种群的产生过程是一个随机过程,每一次新的种群产生只与其父代种群相关,并且种群所处的状态为离散状态,ECAOA算法的这些特点基本符合Markov链的特征.因此,下面我们将用Markov链对ECAOA算法的收敛性进行分析.
定义 21 (有限Markov链) [16]. 随机过程可能取到的值(状态)组成的集合记为S,称为随机过程的状态空间.设随机变量序列{Xn|n≥0}取值于可数状态空间.S=N+={1,2,…,n,…},若对于任意的状态i0,i1,…,in+1∈S,都有
| $P\left\{ {{X}_{n}}_{+1}={{i}_{n}}_{+1}|{{X}_{n}}={{i}_{n}},\ldots ,{{X}_{1}}={{i}_{1}},{{X}_{0}}={{i}_{0}} \right\}=P\left\{ {{X}_{n}}_{+1}={{i}_{n}}_{+1}|{{X}_{n}}={{i}_{n}} \right\}$ | (22) |
成立,则称{Xn|n≥0}为可数状态Markov链.如果状态集S中状态是有限的,则称此Markov链{Xn|n≥0}为有限Markov链.
定义 22 [16]. 如果对任意的i,j∈S,Markov链{Xn|n≥0}的一步转移概率pij(n)与初始时刻n无关,则称该Markov链是齐次的Markov链.
定理 1. ECAOA算法的种群系列{Xn|n≥0}是有限的齐次Markov链.
证明:本文用m表示为每个抗体的基因位数,l为每位基因用二进制表示的位数,|A(t)|为种群规模.设Ω为所有抗体的空间,其每个坐标分别是Ω中的抗体.亲和度函数aff(x)是集合Ω⊂Rn上大于0的连续函数,并定义若x∉Ω,则aff(x)=0.抗体空间Ω={0,1}ml中共有2ml个状态,所以抗体空间W|A(t)|所在的状态空间大小为|A(t)|x2ml.因此,抗体种群序列空间中的状态数目是有限的.
ECAOA算法的状态转移情况可以用如下的随机过程来描述:
| $A(t)\xrightarrow{克隆}B(t)\xrightarrow{变异}C(t)\xrightarrow{交叉}D(t)\xrightarrow{选择}E(t)\xrightarrow{克隆抑制}F(t)\xrightarrow{种群更新}A(t+1),$ |
其中,下标t表示进化的代数.令T=TdoTroTsoTcoTmoTk,则xi(n+1) =T[X(n)i]=TdoTroTsoTcoTmoTk[X(n)i].
根据前面对ECAOA算法各算子的分析以及前面的定义可知,ECAOA算法的种群序列状态转移概率如下:
| $\begin{align} & {{p}_{ij}}(n)={{p}_{n}}\{X(n+1)=Y|X(n)=X\} \\ & \text{ }={{p}_{n}}\{Y|X\} \\ & \text{ }=\coprod\limits_{i=1}^{|A(t)|}{\left\{ \sum\limits_{i}{p\{{{T}_{k}}{{(X(N))}_{i}}={{x}_{i}}(n)\}}\times p\{{{T}_{m}}({{x}_{i}}(n))={{x}_{i}}(n)\}\times p\{{{T}_{c}}({{x}_{i}}(n))={{x}_{i}}(n)\}\times \right.} \\ & \text{ }\left. \underset{{}}{\overset{{}}{\mathop{{}}}}\,p\{{{T}_{s}}({{x}_{i}}(n))={{x}_{i}}(n)\}\times p\{{{T}_{r}}({{x}_{i}}(n))={{y}_{i}}(n)\} \right\}\times \coprod\limits_{i=1}^{A(t)|}{p\{{{T}_{d}}(Y(n))={{x}_{i}}(n+1)\}}. \\ \end{align}$ |
根据前面对ECAOA算法的克隆、变异、交叉、选择、克隆抑制和种群更新操作的定义,计算出的ECAOA算法中抗体群的状态转移概率pij(n)与参数时刻n无关.所以,ECAOA的种群序列{Xn|n≥0}是有限的齐次Markov链.
在模拟退火算法中,模拟退火的过程可以描述为从一个状态转移到另一个状态的随机游动.利用Markov链的性质,分析模拟退火算法对应Markov链的周期性和不可约性,可以证明在一定条件下模拟退火算法的全局收敛性[16].根据模拟退火的Metropolis准则,如果进行以下假设:当Df=f(X)-f(X')>0时,设Df≥t,t为某个充分小的正数,或比温度t的收敛阶小,根据文献[17]中的证明,可以得到如下结论:
定理 2. 设在一定温度t下,模拟退火算法产生的点列为X(k+1) (t),若新解产生满足D~N(0,s2),则当温度t→0时,点列$\{{{X}^{(k)}}(t)\}_{k=1}^{+\infty }$以概率为1收敛于全局极小点,即
| $P(\underset{k\to \infty }{\mathop{\lim }}\,\underset{t\to 0}{\mathop{\lim }}\,f({{X}^{(k)}}(t))={{f}^{*}})=1$ | (23) |
在文献[17]中,黄友锐等人利用齐次有限马尔可夫链的方法证明了基于二进制编码的克隆选择算法的全局收敛性能:
定理 3. 二进制编码的克隆选择算法CSA是以概率1收敛的.
推论 1. ECAOA算法是以概率1收敛的.
证明:本文提出的高效克隆退火优化算法,是在克隆选择算法的基础上引入了模拟退火的思想.由于本文设计的ECAOA算法只是在经典的克隆选择算法的基础上采用模拟退火进制进行种群抗体的改良操作,而模拟退火机制根据定理2中的描述是以概率为1收敛于全局极小点,ECAOA算法的执行过程并没有改变克隆选择算法的本质特征.因此,定理3对ECAOA算法同样适用.我们设{Xn|n≥0}是ECAOA算法的一个随机变量序列,那么当算法迭代到足够多的次数后,下面的公式一定成立:
| $P\{\underset{n\to \infty }{\mathop{\lim }}\,({{X}_{n}}={{S}^{*}})\}=1$ | (24) |
根据定义15可知,种群序列{Xn|n≥0}中包含全局最优解的概率接近1,ECAOA算法是以概率1收敛的.
5 ECAOA算法的计算复杂度分析本节分析ECAOA算法的计算复杂度主要考虑时间复杂度,即主要通过算法指令被执行最大次数来估计算法运行所需的计算量.为了更好地描述算法的时间复杂度,特进行以下定义:
定义 23. 给定自然数n的两个函数F(n)和G(n),当且仅当存在一个正常数K和n0,使得当n≥n0时,有F(n)≤KG(n),则称函数F(n)以函数G(n)为界,记作F(n)=O(G(n)).
在上述定义中,O表示数量级的概念.在分析算法的时间复杂度时,可通过复杂度函数主要项的阶O(G(n))进行表示.ECAOA算法中包含3个参数,即,种群规模N=|A(t)|、抗体的基因位数l、群体的克隆规模M.算法主要包括以下7个操作:(1) 计算抗体的亲和度值;(2) 克隆操作;(3) 变异操作;(4) 交叉操作;(5) 选择操作;(6) 克隆抑制操作;(7) 种群更新操作.在抗体群中,由于要对每个抗体计算亲和度值,所以操作(1) 的执行次数是N.操作(2) 对抗体群进行克隆操作所需的执行次数是M.操作(3) 采取变异操作所需的最多次数为N.操作(4) 采取的交叉操作所需的计算量最多为log2N.根据本文对选择操作的定义,操作(5) 采取的选择操作由于要计算每个抗体的增强度,导致所需的计算量较大,最多次数为(N-1) xN+1.操作(6) 和操作(7) 所采取的操作需要的执行次数均是1.由于N>M,N>log2N,于是,第n次迭代中ECAOA算法执行操作的总次数Sn应该符合如下的条件:
Sn≤N+M+N+log2N+(N-1) xN+1+2<N2+3N.
因此,ECAOA算法的计算量最高级为O(N2),这表明种群规模直接影响到算法的搜索速度.在CSA算法中,抗体要依次经过克隆、变异、选择、克隆抑制和种群更新等操作,计算复杂度的最高级别也为O(N2)[17].但是,ECAOA算法通过引入交叉操作和模拟退火的策略,每次产生的新抗体都先进行Metropolis准则判断,有效保证子抗体比父抗体更加优良,从而跳出局部极优值,避免了CSA算法可能出现的早熟收敛现象,因而同一进化代数中能够更快、更好地找到满意解,使得满足同样收敛条件的时间要快于CSA算法.
6 ECAOA算法在数据挖掘中的应用近年来,信息爆炸性的递增导致Web用户面对越来越多的海量数据,如何从海量的数据中提取有用的知识已经成为当务之急.数据挖掘(data mining)就是为了顺应这种需要发展起来的一种数据处理技术.现代数据挖掘方法主要依靠模式提取技术,为了改善和提高数据挖掘功能、性能和效率,发展趋势是集成多种技术的综合方法[18],如,将免疫理论与统计学集成的免疫控制图挖掘方法、基于免疫策略的数据挖掘方法、基于免疫规划的广义规则推理方法、基于免疫多变量子波神经网络的数据挖掘方法等.为了检验本文设计的ECAOA算法的有效性,下面将ECAOA算法应用到关联规则挖掘中.
为了验证本文设计的ECAOA算法的有效性,分别基于census数据集和chess数据集平台进行了两类对比实验:
(1) ECAOA算法与其他智能优化算法:遗传算法(genetic algorithm,简称GA)算法、SA算法和CSA算法.
(2) ECAOA算法与其他3种典型的关联规则挖掘算法:Apriori算法、DHP算法和FP-Growth算法.Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法.DHP(direct hashing and pruning)是一种基于散列技术的Apriori算法的改良方法.FP-Growth(frequent pattern growth)算法在保留项集关联信息的同时,将提供频繁项集的数据库压缩成一棵频繁模式树(FP-tree),同时依然保留其中的关联信息.
Census数据集是由美国加利佛尼亚大学信息与计算机科学系提供的、专供数据挖掘和机器学习用的一个测试数据库.它的大小为10.9M,共包含48 842条记录,每条记录有14个属性.Chess数据集共包含3 196条记录,共含有75个项,属于一种稠密的数据集[19].
第1类实验主要从响应时间、执行时间、品质因数、误差性能和群体多样性这5个方面进行比较,在census数据集上的实验结果如图 2~图 6所示.

|
Fig. 2 Comparison of the response time of the four algorithms in census data set 图 2 Census数据集上4种算法的响应时间比较 |
|
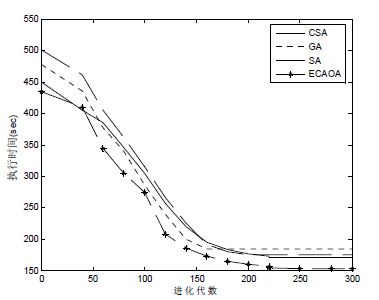
Fig. 3 Comparison of the execution time of the four algorithms in census data set 图 3 Census数据集上4种算法的执行时间比较 |

|
Fig. 4 Comparison of the quality factor of the four algorithms in census data set 图 4 Census数据集上4种算法的品质因数比较 |
|
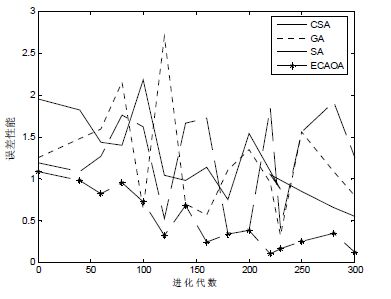
Fig. 5 Comparison of the error performance of the four algorithms in census data set 图 5 Census数据集上4种算法的误差性能比较 |

|
Fig. 6 Comparison of the population diversity of the four algorithms in census data set 图 6 Census数据集上4种算法的群体多样性比较 |
图 2的实验结果显示:在进化前期(进化代数大约为70) ,GA算法的性能表现最优,CSA算法的性能表现最差,ECAOA算法的性能稍微强于SA算法;在进化的中期(进化代数大约为70~160) ,ECAOA算法的性能表现最优,GA,CSA和SA三者之间的性能互有优劣;在进化的后期,GA算法最先收敛,ECAOA算法的优势表现得最为明显,其响应时间大概只是GA算法的71.42%,SA算法和CSA算法的响应时间几乎相同.
在图 3和图 4中,ECAOA算法在进化中后期的执行时间和品质因数方面都表现出良好的性能,其执行时间比CSA算法大约少9.87%,比SA算法大约少11.23%,比GA算法大约少13.89%,其品质因数比CSA算法大约提高6.85%,比SA算法大约提高17.67%,比GA算法大约提高21.36%.
在图 5显示的误差性能方面,4种算法在不同进化代数时测试出的误差性能基本都不相同,ECAOA算法在大多数情况下优于其他3种算法.在图 6的实验结果中,ECAOA算法在大约进化到155次时获得了最高的群体多样性值3.62.在进化的前半阶段,随着进化的逐渐深入,4种算法的群体规模在不断地扩大,从而群体的多样性在显著地增强;在进化的后半阶段,随着算法逐渐找到满意解并缓慢开始收敛,算法的规模在逐步缩小导致群体的多样性显著的降低.ECAOA算法的平均群体的多样性值为1.75,CSA算法的平均群体的多样性值为1.68,SA算法的平均群体的多样性值为1.65,GA算法的平均群体的多样性值为1.61.
在chess数据集上的实验结果如图 7~图 11所示.图 7的实验结果显示:在进化前期(进化代数大约为140) ,CSA算法的性能表现最优,ECAOA算法的性能和GA算法比较接近,但稍微强于SA算法;在进化的后期,ECAOA算法的性能表现最优,其响应时间大概只有GA算法的76.83%,只有SA算法的84.41%,只有CSA算法的82.67%.在图 8中,ECAOA算法的执行时间在进化中后期的大多数情况下都表现出良好的性能,但是4种算法的整体性能都非常接近.在图 9中,ECAOA算法的品质因数在进化期间都表现得非常稳定,其品质因数比CSA算法大约提高1.82%,比SA算法大约提高12.42%,比GA算法大约提高9.84%.

|
Fig. 7 Comparison of the response time of the four algorithms in chess data set 图 7 Chess数据集上4种算法的响应时间比较 |

|
Fig. 8 Comparison of the execution time of the four algorithms in chess data set 图 8 Chess数据集上4种算法的执行时间比较 |

|
Fig. 9 Comparison of the quality factor of the four algorithms in chess data set 图 9 Chess数据集上4种算法的品质因数比较 |
|
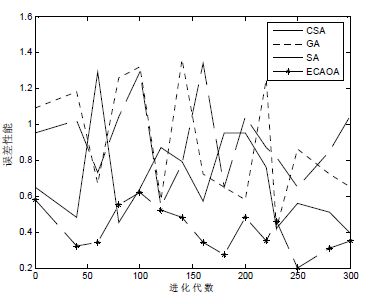
Fig. 10 Comparison of the error performance of the four algorithms in chess data set 图 10 Chess数据集上4种算法的误差性能比较 |

|
Fig. 11 Comparison of the population diversity of the four algorithms in chess data set 图 11 Chess数据集上4种算法的群体多样性比较 |
在图 10显示的误差性能方面,4种算法在不同进化代数时,ECAOA算法的平均误差性能大约是0.32,CSA,GA和SA算法的平均误差性能分别大约是0.68,0.71,0.82.在图 11的实验结果中,ECAOA算法在大约进化到168次时,获得了最高的群体多样性值3.41.群体的多样性在进化的前期都逐渐扩大,在进化的后期都显著地降低.ECAOA,CSA,SA,GA算法的平均群体的多样性值分别为1.65,1.61,1.55,1.58.
通过第1类实验,我们不难分析出,ECAOA算法在响应时间、执行时间、品质因数、误差性能和群体多样性这5方面都表现出良好的性能.这主要是因为ECAOA算法在变异和交叉等操作产生新的抗体后,首先通过模拟退火的Metropolis准则来决定新抗体是否保留,从而有效保证新的抗体具有更好的性能.ECAOA算法将CSA算法和SA算法的优点进行结合,有效避免了陷入局部极优值,能够有效改良算法的品质因数、误差性能和群体多样性等性能指标参数.在进化前期,ECAOA算法的性能与其他3种算法相比并没有表现出明显的优势,相反,在局部情况下,其性能还比较落后.导致这种情况的原因是,ECAOA算法在进行首次选择操作时要计算每个抗体的增强度,从而增大了所需的计算量.CSA算法在绝大多数情况下的性能要优于SA算法和GA算法,主要是克隆操作不仅扩大了解的空间范围,而且提高了优良抗体的比例,这样将积极影响到群体多样性和误差性能等性能指标参数.GA算法在大多数情况下的性能表现不如其他3种算法,主要是因为该算法很容易出现早 熟收敛现象,导致其群体多样性较差,误差性能较大.
为了更好地评估ECAOA算法的性能,本节结合算法的执行时间、挖掘的关联规则数目和关联规则准确率对算法的挖掘质量进行如下定义:
定义 24. 如果算法挖掘的关联规则数目用total表示,算法的执行时间用te表示,关联规则的准确率用θ表示,则算法的挖掘质量φ描述如下:
| $\varphi =\frac{total\times \theta }{{{t}_{e}}}$ | (25) |
从公式(25) 中不难分析出:执行时间te越少,关联规则数目total越大,准确率θ越高,则算法的挖掘质量φ越大,算法的整体性能越优良.
第2类实验主要从运行时间、关联规则数目、准确率和挖掘质量这4个方面进行比较,在census数据集上的实验结果如图 12~图 15所示.
|
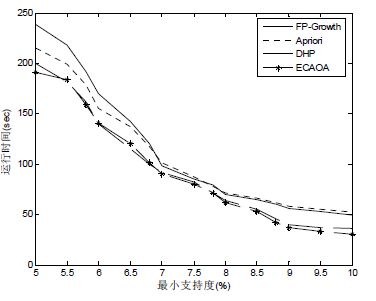
Fig. 12 Comparison of the execution time of the four algorithms in census data set 图 12 Census数据集上4种算法的运行时间比较 |

|
Fig. 13 Comparison of number of association rules of the four algorithms in census data set 图 13 Census数据集上4种算法的关联规则数目比较 |
|
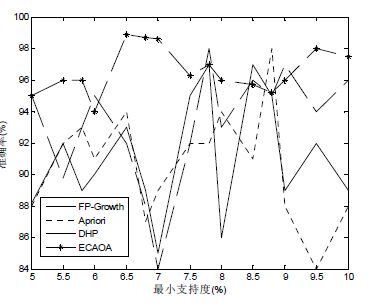
Fig. 14 Comparison of the accuracy rate of the four algorithms in census data set 图 14 Census数据集上4种算法的准确率比较 |
|
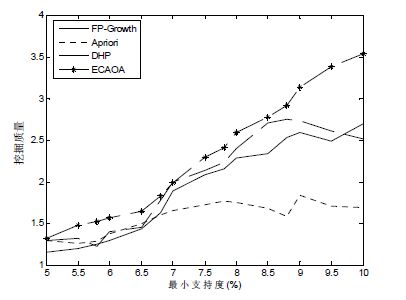
Fig. 15 Comparison of the mining quality of the four algorithms in census data set 图 15 Census数据集上4种算法的挖掘质量比较 |
在图 12的执行时间对比实验中,当最小支持度小于7.8%时,ECAOA算法和DHP算法的性能非常接近,Apriori算法和FP-Growth算法的性能表现得相对较差;当最小支持度大于7.8%时,ECAOA算法的优势最明显,而Apriori算法和FP-Growth算法的执行时间几乎相等,其运行时间比DHP算法大约要少10s,比Apriori算法和FP-Growth算法大约要少28s.在图 13中,当最小支持度在5.75%~7%范围时,4种挖掘算法得到的关联规则数目非常接近;当最小支持度大于7%时,ECAOA算法和DHP算法都表现出良好的性能,其挖掘出的关联规则数目比DHP算法大约多5.07%,比FP-Growth算法和Apriori算法大约多25.23%.
在图 14中,ECAOA算法的准确率平均达到95.88%,FP-Growth,Apriori和DHP算法的准确率平均分别为90.39%,94.08%,93.92%.在图 15显示的挖掘质量对比中,ECAOA算法的优势表现得非常明显,随着最小支持度的逐渐变大,ECAOA算法的挖掘质量明显提高.
|
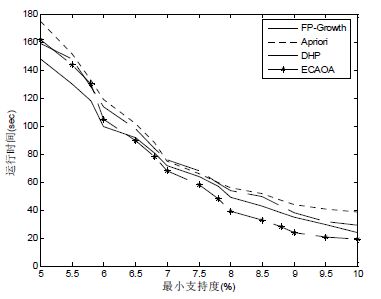
Fig. 16 Comparison of the execution time of the four algorithms in chess data set 图 16 Chess数据集上4种算法的运行时间比较 |

|
Fig. 17 Comparison of number of association rules of the four algorithms in chess data set 图 17 Chess数据集上4种算法的关联规则数目比较 |

|
Fig. 18 Comparison of the accuracy rate of the four algorithms in chess data set 图 18 Chess数据集上4种算法的准确率比较 |

|
Fig. 19 Comparison of the mining quality of the four algorithms in chess data set 图 19 Chess数据集上4种算法的挖掘质量比较 |
在图 16的运行时间对比实验中,当最小支持度小于6.5%时,ECAOA算法与Apriori算法和DHP算法三者表现出来的性能互有优劣,但是FP-Growth算法的性能表现得相对较好;当最小支持度大于6.5%时,ECAOA算法的优势最明显,随着最小支持度逐渐变大,ECAOA算法的运行缓慢减少.在图 17中,当最小支持度小于6.8%时,ECAOA算法的性能稍微优于Apriori,DHP,FP-Growth算法;当最小支持度大于6.8%时,ECAOA算法表现出优良的性能,其挖掘出的关联规则数目比FP-Growth算法大约多9.38%,比Apriori算法大约多21.45%,比DHP算法大约多23.68%.
在图 18中,ECAOA算法的准确率平均达到97.05%,FP-Growth,Apriori和DHP算法的准确率平均分别为93.12%,94.67%,90.32%.在图 19显示的挖掘质量对比中,随着最小支持度的不断变大,ECAOA算法的挖掘质量逐渐提高.当最小支持度大于6.8%时,ECAOA算法的性能最优良,Apriori算法的性能表现最差,DHP算法的性能最不稳定.
通过第2类实验,我们不难分析出:ECAOA算法在绝大多数情况下,在运行时间、关联规则数目、准确率这3方面的性能都要稍微超过其他3种挖掘算法,在挖掘质量方面则明显优于其他3种挖掘算法.这主要是因为ECAOA算法充分结合了克隆选择算法和模拟退火算法的优点,在每次挖掘过程中都采取并行的方式进行搜索,同时在算法的执行过程,总是将优良的抗体在群体中的规模不断扩大,变异和交叉操作又不断地丰富了种群的多样性,并且将生存度最高的抗体通过克隆抑制操作直接保留到下一代,同时,种群更新操作将性能较差的抗体直接进行删除.ECAOA算法在整个数据挖掘期间充分体现出人工免疫算法所具备的并行性和鲁棒性特征. Apriori算法在大多数情况下的性能表现都不如DHP和FP-Growth算法,主要是因为其挖掘的规则存在大量冗余,并且算法需要多次扫描数据库,导致所消耗的时间较大,而DHP算法通过使用TID,避免了反复读取事务数据库,FP-Growth算法将频繁项集的数据库压缩成一棵频繁模式树的方式,能够有效提高算法的执行效率.
通过应用ECAOA,CSA,GA,SA,Apriori,DHP和FP-Growth算法对census和chess数据集从不同方面进行测试,实验结果显示了本文设计的ECAOA算法具有较快的执行时间和较强的搜索能力,能够有效地避免CSA算法可能存在的早熟收敛现象,同时具有良好的品质因数、挖掘质量和群体多样性,能够成功地应用于数据挖掘领域中.
7 结束语针对传统的克隆选择算法可能存在的早熟收敛现象和缺少交叉操作问题,提出一种高效的克隆优化退火算法ECAOA.它结合了模拟退火算法与免疫系统的克隆选择机制,并根据退火选择概率进行选择操作,同时,根据模拟退火的Metropolis接受准则设计了交叉操作,不仅能够有效保持全局搜索和局部搜索的平衡,而且可以有效提高算法的搜索效率,从而加快算法的收敛速度.在第1类数据挖掘实验测试中,ECAOA算法在响应时间、执行时间、品质因数、误差性能和群体多样性这5个方面与CSA,SA,GA算法相比都表现出较好的性能.在第2类数据挖掘实验测试中,ECAOA算法在绝大多数情况下,在运行时间、关联规则数目、准确率这3个方面的性能都要稍微超过其他3种挖掘算法,在挖掘质量方面,则明显优于其他3种挖掘算法,并解决了传统的克隆选择算法可能存在的早熟收敛问题.
| [1] | Mohammadi M, Raahemi B, Akbari A, Nassersharif B, Moeinzadeh H. Improving linear discriminant analysis with artificial immune system-based evolutionary algorithms. Information Sciences, 2012, 189 (4) :219–232. [doi:10.1016/j.ins.2011.11.032] |
| [2] | Naderi B, Khalili M, Tavakkoli-Moghaddam R. A hybrid artificial immune algorithm for a realistic variant of job shops to minimize the total completion time. Computers & Industrial Engineering, 2009, 56 (4) :1494–1501. [doi:10.1016/j.cie.2008.09.031] |
| [3] | Molla-Alizadeh-Zavardehi S, Hajiaghaei-Keshteli M, Tavakkoli-Moghaddam R. Solving a capacitated fixed-charge transportation problem by artificial immune and genetic algorithms with a Prüfer number representation. Expert Systems with Applications, 2011, 38 (8) :10462–10474. [doi:10.1016/j.eswa.2011.02.093] |
| [4] | Aragón VS, Esquivel SC, Coello Coello CA. An immune algorithm with power redistribution for solving economic dispatch problems. Information Sciences, 2015, 295 (2) :609–632. [doi:10.1016/j.ins.2014.10.026] |
| [5] | Ulutas BH, Kulturel-Konak S. An artificial immune system based algorithm to solve unequal area facility layout problem. Expert Systems with Applications, 2012, 39 (5) :5384–5395. [doi:10.1016/j.eswa.2011.11.046] |
| [6] | Liu RC, Zhu BB, Bian RY, Ma YJ, Jiao LC. Dynamic local search based immune automatic clustering algorithm and its applications. Applied Soft Computing, 2015, 27 (2) :250–268. [doi:10.1016/j.asoc.2014.11.026] |
| [7] | Aydin I, Karakose M, Akin E. A multi-objective artificial immune algorithm for parameter optimization in support vector machine. Applied Soft Computing, 2011, 11 (1) :120–129. [doi:10.1016/j.asoc.2009.11.003] |
| [8] | Sakthivel VP, Bhuvaneswari R, Subramanian S. Artificial immune system for parameter estimation of induction motor. Expert Systems with Applications, 2010, 37 (8) :6109–6115. [doi:10.1016/j.eswa.2010.02.034] |
| [9] | Turkoglu I, Didem Kaymaz E. A hybrid method based on artificial immune system and k-NN algorithm for better prediction of protein cellular localization sites. Applied Soft Computing, 2009, 9 (2) :497–502. [doi:10.1016/j.asoc.2008.07.003] |
| [10] | Hussain AJ, Fergus P, Al-Askar H, Al-Jumeily D. Dynamic neural network architecture inspired by the immune algorithm to predict preterm deliveries in pregnant women. Neurocomputing, 2015, 151 (3) :963–974. [doi:10.1016/j.neucom.2014.03.087] |
| [11] | Yu HM, Yao PJ. Combined genetic algorithm/simulated annealing algorithm for large-scale system energy integration. Computers and Chemical Engineering, 2000, 8 (24) :2023–2035. [doi:10.1016/S0098-1354(00)00601-3] |
| [12] | Ling J, Cao Y, Ying JH, Xu GX, Huang TX. An algorithm for Generating diverse antibody based on niche technology. Acta Electronica Sinica, 2003, 31 (8) :1130–1133(in Chinese with English abstract). [doi:10.3321/j.issn:0372-2112.2003.08.003] |
| [13] | Xi GY, Yue JP, Zhou BX, Tang P. Application of an artificial immune algorithm on a statistical model of dam displacement. Computers & Mathematics with Applications, 2011, 62 (10) :3980–3986. [doi:10.1016/j.camwa.2011.09.057] |
| [14] | Mohammad AH, Zitar RA. Application of genetic optimized artificial immune system and neural networks in spam detection. Applied Soft Computing, 2011, 11 (4) :3827–3845. [doi:10.1016/j.asoc.2011.02.021] |
| [15] | Li SZ, Li MY, Pan YX. Genetic annealing algorithm and its convergence analysis. Control Theory and Applications, 2001, 19 (3) :376–381. http://cn.bing.com/academic/profile?id=2347279387&encoded=0&v=paper_preview&mkt=zh-cn |
| [16] | Duan HB, Zhang XY, Xu CF. Bio-Inspired Computing. Beijing: Science Press, 2010 : 98 -105(in Chinese with English abstract). |
| [17] | Huang YR. Intelligent Optimization Algorithm and Its Application, 2008 :198–210(in Chinese with English abstract). |
| [18] | Farzanyar Z, Kangavari M, Cercone N. Max-FISM:Mining (recently) maximal frequent itemsets over data streams using the sliding window model. Computers & Mathematics with Applications, 2012, 64 (6) :1706–1718. [doi:10.1016/j.camwa.2012.01.045] |
| [19] | Yang BR, Li JH, Song W, Li X. KD (D & K):A new knowledge discovery process model for complex systems. Acta Automatic Sinica, 2007, 33 (2) :151–155(in Chinese with English abstract). [doi:10.1360/aas-007-0151] |
| [12] | 凌军, 曹阳, 尹建华, 徐国雄, 黄天锡. 基于小生境技术的多样性抗体生成算法. 电子学报, 2003,31 (8) :1130–1133. [doi:10.3321/j.issn:0372-2112.2003.08.003] |
| [16] | 段海滨, 张祥银, 徐春芳. 仿生智能计算. 北京: 科学出版社, 2010 : 98 -105. |
| [17] | 黄友锐. 智能优化算法及其应用, 2008 :198–210. |
| [19] | 杨炳儒, 李晋宏, 宋威, 李欣. 面向复杂系统的知识发现过程模型KD(D & K)及其应用. 自动化学报, 2007,33 (2) :151–155. [doi:10.1360/aas-007-0151] |
 2016, Vol. 27
2016, Vol. 27


