建筑几何是计算机辅助设计和图形学中一个新兴的研究领域, 它基于传统的曲线曲面设计理论及新兴的离散微分几何理论, 利用计算机辅助几何设计技术和数字几何处理方法, 进行建筑结构的建模与处理, 并解决建筑结构设计中的一系列技术难题.

在经典的微分几何理论中, 极小曲面是指插值给定边界曲线的面积最小的曲面, 其平均曲率处处为0^{[1, 2]}.由于其特有的内在几何性质, 极小曲面在建筑几何设计、飞机外形设计、仿生学、纳米建模等领域具有重要的应用价值^[3].特别地, 在建筑几何中, 极小曲面是张拉膜等空间建筑结构的理想几何形状.因而, 以几何设计与计算的视角, 研究极小曲面的快速几何建模问题, 对建筑几何这一新兴研究领域的发展具有重要意义.

与三角网格相比, 按照四边网格(以四边形为主导的网格)所构建的空间结构具有重量较轻、成本较低、更加符合人们对几何形状变化的自然感知等特点, 因而在玻璃结构和钢结构中, 四边网格表现出更好的优越性.由于在实际应用中玻璃结构和钢结构等新兴建筑结构均以离散四边网格曲面为表现形式, 因此, 研究以四边网格为表现形式的离散极小曲面的高效建模方法, 便成为当务之急.

基于以上应用背景, 在本文中我们主要研究如下问题:即给定一条封闭的边界离散折线, 如何构造以其为边界的离散四边网格极小曲面.首先从曲面的内蕴微分几何度量出发, 我们给出了离散四边网格极小曲面的数学定义方法; 然后基于保长度边界投影、四边网格生成、径向基函数插值映射和多层次非线性优化技术, 提出了由给定边界离散折线快速构造离散四边网格极小曲面的一般框架.最后通过若干建模实例, 验证了本文方法的有效性, 并研究了其在玻璃结构及钢结构建模中的应用.

1 相关工作

极小曲面一直是经典微分几何领域的重要研究对象.自从Jin等人首次将极小曲面引入几何设计与计算领域以来^[4], 已有不少学者从CAGD的视角对参数形式的极小曲面造型问题进行了研究.具体可参考作者对CAGD中参数形式极小曲面造型的研究进展所做的综述^[5].按照建模方式的不同, 可将此领域的相关工作分为两大类, 即精确造型方法和逼近造型方法.目前, CAGD中极小曲面的精确造型方法主要有两大方面的内容:一是某些特殊极小曲面的控制网格表示与构造^[6-8], 二是等温参数多项式极小曲面的挖掘与性质^[9-11].逼近造型方面的工作大体可以分为3类:基于线性偏微分方程的逼近方法^{[12, 13]}; 基于能量函数最优化的逼近方法^[14-19]; 基于数值计算的逼近方法^[20-22].

Plateau问题是极小曲面理论中的经典问题, 即如何寻找以给定的空间可求长Jordan闭曲线为边界的极小曲面.为了找到Plateau问题的Bézier近似解, Monterde提出了Plateau-Bézier问题^[14], 即在所有的插值给定边界曲线的Bézier曲面中找到最小面积的曲面, 并利用Dirichlet能量函数极小化的方法近似求解.随后, Wu等人将Dirichlet方法推广到Plateau-B样条问题^[16]以及Plateau-NURBS问题^[17]; Xu等人基于平均曲率提出了一种新的能量函数, 对Dirichlet方法进行了改进^[18].Hao等人研究了非多项式空间中quasi-Bézier极小曲面的求解问题^[19].Pan等人利用平均曲率流方法研究了细分极小曲面的约束建模方法^[23]; Li等人则研究了基于测地线约束的近似极小曲面的造型问题^[24].

与参数形式极小曲面相比, 离散极小曲面造型方面的相关工作比较少, 而面向建筑几何的离散极小曲面的研究工作更是凤毛麟角.Pinkall和Polthier基于离散Dirichlet能量来近似求解共性映射和离散Plateau问题^[25]. Dziuk和Hutchinson运用有限元方法求解离散Plateau问题^[26].Zhang等人研究了加权极小曲面与加权离散极小曲面的性质及其构造^[27]; Bobenko等人研究了以圆为基本单元的离散极小曲面的构造方法^[28].Wallner等人研究了以圆锥网格为表示形式的离散极小曲面的对偶构造方法^[29].Pan等人利用CVT技术研究了三角网格常平均曲率曲面的优化问题^[30], 在优化的同时可以有效地提高三角网格单元质量.目前, 针对四边网格曲面的离散Plateau问题还鲜有研究工作提及.

2 离散四边网格极小曲面及问题描述 2.1 离散四边网格极小曲面的定义

假设r(u, v)为一张参数曲面, 其第1基本形式的系数为

$ E = \left\langle {{r_u}, {r_u}} \right\rangle, F = \left\langle {{r_u}, {r_v}} \right\rangle, G = \left\langle {{r_v}, {r_v}} \right\rangle, $

其中, r_u, r_v是r(u, v)中分别对u和v的一阶偏导数和定义向量的点积.

r(u, v)的第2基本形式的系数为

$ L = \left\langle {{r_u}, {r_v}, {r_{uu}}} \right\rangle, M = \left\langle {{r_u}, {r_v}, {r_{uv}}} \right\rangle, N = \left\langle {{r_u}, {r_v}, {r_{vv}}} \right\rangle, $

r_uu, r_uv是r(u, v)中分别对u和v的二阶偏导数和定义向量的混合乘积.

曲面r(u, v)的面积A可由下式计算:

$ A = \int\limits_U {\sqrt {EG - {F^2}} } {\rm{d}}u{\rm{d}}v $

(1)

r(u, v)的平均曲率H则可由下式计算而得:

$ H = \frac{{EN - 2FM + LG}}{{2(EG - {F^2})}}. $

若曲面r(u, v)的平均曲率H处处为0, 则称r(u, v)为极小曲面, 即是以给定曲线为边界的所有曲面中面积最小的曲面.

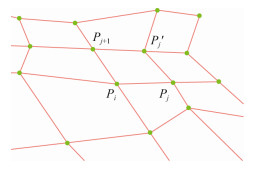
对于离散四边网格曲面, 如何定义其在顶点处的平均曲率, 是离散微分几何中的一个难点问题.本文采用文献[31]中的离散平均曲率定义方法.如图 1所示, 假设P_i, P_j, P_j+1, P'_j这4个顶点组成了四边网格曲面M上的一个离散网格单元E_j, 则可在该单元上定义一个双线性Bézier曲面片S(u, v), 并可计算该曲面片对u和v的一阶偏导分别为

$ \begin{array}{l} {S_u} = (1 - v)({P_{j + 1}} - {P_i}) + v({{P'}_j} - {P_j}), \\ {S_v} = (1 - u)({P_j} - {P_i}) + u({{P'}_j} - {P_{j + 1}}). \end{array} $

由式(1)可知, 该网格单元E_i的面积A_j可由下式计算:

$ {{A}_{j}}=\iint\limits_{U}{\sqrt{{{\left\| {{S}_{u}} \right\|}^{2}}{{\left\| {{S}_{v}} \right\|}^{2}}-{{\left\langle {{S}_{u}}, {{S}_{v}} \right\rangle }^{2}}}}\text{d}u\text{d}v. $

进一步地, 我们可以得到在顶点P_i处的平均曲率向量估计公式为

$ H({P_i}) \approx \frac{2}{{\sum\limits_j {{A_j}} }}\sum\limits_j {[{\alpha _j}({P_j}-{P_i}) + } {\beta _j}({P_{j + 1}}-{P_i}) + {\gamma _j}({P'_j}-{P_i})], $

其中, α_j, β_j, γ_j为与网格单元E_i的几何度量有关的系数, 具体可参考文献[31].易得, 顶点P_i处的平均曲率度量为$\sqrt{{{\left\| H({{P}_{i}}) \right\|}^{2}}}.$基于此, 下面我们给出四边网格离散极小曲面的局部定义方式.

定义1. 若四边网格曲面M上每一个顶点处的平均曲率值$\sqrt{{{\left\| H({{P}_{i}}) \right\|}^{2}}}.$均为0, 则称M为四边网格离散极小曲面.

在一般情况下, 构造满足定义1的四边网格离散极小曲面是十分困难的.基于面积极小化的思想, 我们给出四边网格离散极小曲面的全局定义方式.

定义2. 给定三维空间中的一条封闭离散折线$B=\left\{ {{b_i}} \right\}_{i=0}^N$, 若四边网格曲面M是以该封闭折线为边界的所有四边网格曲面中面积最小的离散曲面, 则称M为四边网格离散极小曲面.

在本文中, 定义1中的平均曲率度量和定义2中的面积度量均将作为四边网格离散极小曲面的优化目标集成到构造框架中.

2.2 问题描述

本文所探讨的离散极小曲面建模问题可描述为:给定三维空间中的一条封闭离散折线$B=\left\{ {{b_i}} \right\}_{i=0}^N$, 如何构造以该折线为边界的四边网格离散曲面, 使其为离散极小曲面.

需要说明的是, 给定封闭的离散折线, 以其为边界的四边网格曲面的顶点连接方式与顶点数目有无穷多种选择.在本文所探讨的问题范畴内, 我们需要首先确定以$B=\left\{ {{b_i}} \right\}_{i=0}^N$为边界的四边网格曲面的拓扑连接关系(即顶点连接方式及网格顶点数目), 然后再通过优化算法来构造在此拓扑连接关系约束下的离散极小曲面.在下一节中我们将详细加以讨论.

3 四边网格离散极小曲面的快速构造方法 3.1 算法框架

在本文中, 我们拟采取的算法大体上可以概括为图 2中的4步.即首先将空间边界折线保长参数化到二维平面上; 然后在参数化投影所得到的二维区域内, 利用四边网格生成算法得到二维区域的四边网格化结果; 接着以所给定的三维空间边界折线作为约束, 运用径向基函数映射插值技术得到初始的四边网格离散曲面; 最后运用约束优化求解方法, 以四边网格上的离散平均曲率度量及面积度量为目标函数, 对所得到的初始网格进行迭代优化, 得到最终的四边网格离散极小曲面.下面我们将分别对每一步骤的技术细节进行详细阐述.

3.2 平面区域约束四边形化

给定三维空间边界折线$B=\left\{ {{b_i}} \right\}_{i=0}^N \in {\Re ^3}$, 我们首先利用文献[32]中的保长度投影参数化方法, 得到其在二维平面上的投影${B^P}=\left\{ {b_i^P} \right\}_{i=0}^N \in {\Re ^2}$, 并尽可能地保持三维空间折线$B=\left\{ {{b_i}} \right\}_{i=0}^N$的长度不变(如图 3所示).在得到空间边界折线的保长度平面投影之后, 下面需要对由该平面折线${B^P}=\left\{ {b_i^P} \right\}_{i=0}^N$所围成的区域Ω^P进行四边形化, 即在该区域的内部用一定数量的四边形网格单元填充起来, 这也是离散极小曲面造型方法中极为关键的一步.本文提出了一种新的四边形网格生成方法, 可生成高质量的四边形网格.该算法的主要步骤如下.

Step 1.将复杂的多连通边界变换为单连通边界, 也就是说, 用一个单连通多边形来代替原来的多连通多边形, 并保证替换前后多边形的几何形状保持一致.这样对于替换后的多边形边界来说, 它将始终是只有一条外部边界的单连通多边形(如图 4(b)所示).

Step 2.将变换后的单连通区域进行拟凸区域分解, 得到一系列简单的拟凸区域(如图 4所示)).

Step 3.对每一个拟凸区域, 利用模板方法生成四边网格的拓扑连接结构, 然后根据模板域每条边侧所对应实际域中的边界, 计算其每个顶点的权值, 并确定参数域中边界顶点的位置坐标信息.

Step 4.利用拉普拉斯网格光顺技术, 对内部生成的拓扑顶点进行光顺处理, 并得到每个内部顶点的坐标信息(如图 4(d)所示).

在上述算法中, 凸区域划分的作用主要是为了能方便地使用基于模板的平面四边网格拓扑生成方法, 即在每一个划分得到的子区域内利用模板方法生成内部的网格拓扑信息.平面网格的拉普拉斯光滑算子可使内部顶点尽量趋近于其1-邻域顶点的加权平均, 从而使得四边网格单元大小比较均匀, 以得到高质量的平面四边网格, 继而得到质量较好的初始曲面M⁰.

通过上述算法, 我们便可得到拟构造的四边网格曲面的内部拓扑连接信息, 为后续的四边网格极小曲面优化算法打下了基础.

3.3 基于径向基函数约束插值映射的初始四边网格生成

在上一步, 已生成平面投影折线所包围区域Ω^P的四边形化网格${M^P} \in {\Re ^2}, $下面需要将该平面四边网格M^P映射到三维空间${\Re ^3}, $得到三维空间四边网格曲面${M^0} \in {\Re ^2}, $并且使得初始网格曲面M⁰插值预先给定的三维空间折线$B=\left\{ {{b_i}} \right\}_{i=0}^N$.为了解决这一问题, 本文借鉴径向基函数插值映射技术来构造插值给定边界的初始网格曲面M⁰.将三维空间折线B上的顶点$\left\{ {{b_i}} \right\}_{i=0}^N$和二维平面折线B^P上的顶点$\left\{ {b_i^P} \right\}_{i=0}^N$作为约束, 平面四边网格M^P上的顶点可通过径向基函数映射到待求的初始网格曲面M⁰上.特别地, 该径向基函数映射可表示为如下形式.

$ f(x) = \sum\limits_{j = 1}^N {{d_j}} \phi (x - b_j^P) + g(x) $

(2)

其中, $\left\{ {b_i^P} \right\}_{i=0}^N$为平面四边网格M^P的边界约束点, d_j为待求的权值, g(x)为线性多项式函数.

为求解权值d_j, 由b_i=f(b_i^P)可得

$ b_i^{} = \sum\limits_{j = 1}^N {{d_j}} \phi (b_i^P - b_j^P) + g(b_i^P) $

(3)

因此, 我们可以通过求解一个线性方程组来得到d_j和g(x)的系数.

令$b_j^P=(v_i^{P, x}, v_i^{P, y}, v_i^{P, z}), {\phi _{ij}}=\phi (b_i^P -b_j^P)$, 则该线性方程组可表示为

$ \left[{\begin{array}{*{20}{c}} {{\phi _{11}}}&{{\phi _{12}}}& \ldots &{{\phi _{1k}}}&1&{v_1^{P, x}}&{v_1^{P, y}}&{v_1^{P, z}}\\ {{\phi _{21}}}&{{\phi _{22}}}& \ldots &{{\phi _{2k}}}&1&{v_2^{P, x}}&{v_2^{P, y}}&{v_2^{P, z}}\\ \vdots & \vdots &{}& \vdots & \vdots & \vdots & \vdots & \vdots \\ {{\phi _{k1}}}&{{\phi _{k2}}}& \ldots &{{\phi _{kk}}}&1&{v_k^{P, x}}&{v_k^{P, y}}&{v_k^{P, z}}\\ 1&1& \ldots &1&0&0&0&0\\ {v_1^{P, x}}&{v_2^{P, x}}& \ldots &{v_k^{P, x}}&0&0&0&0\\ {v_1^{P, y}}&{v_2^{P, y}}& \ldots &{v_k^{P, y}}&0&0&0&0\\ {v_1^{P, z}}&{v_2^{P, z}}& \ldots &{v_k^{P, z}}&0&0&0&0 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{d_1}}\\ {{d_2}}\\ \vdots \\ {{d_k}}\\ {{p_0}}\\ {{p_1}}\\ {{p_2}}\\ {{p_3}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ \vdots \\ {{b_k}}\\ 0\\ 0\\ 0\\ 0 \end{array}} \right] $

(4)

其中, Φ(r)为具有紧支撑性质的Wendland径向基函数,

$ \phi (r) = (1 - r)_ + ^6(3 + 18r + 35{r^2}), $

其中, 紧支撑集半径为$r=\frac{{{{\left\| {\bar x} \right\|}_2}}}{\lambda }, {a_ + }={\rm{max}}\{ a, 0\}.$

由于本文利用了具有紧支撑性质的径向基函数, 因而线性系统(4)的系数矩阵是一个稀疏矩阵, 可通过LU分解方法快速求解.求解得到d_j和g(x)的系数之后, 我们便可通过式(2)中的f(x)将平面四边网格M^P上的顶点映射得到初始网格曲面M⁰, 并且插值预先给定的三维空间折线$B=\left\{ {{b_i}} \right\}_{i=0}^N.$

3.4 离散极小曲面优化算法

在得到初始的离散网格曲面M⁰之后, 本节将研究如何得到最终的四边网格离散极小曲面.通过任意的给定边界折线, 若构造严格满足定义1(即平均曲率处处为0)的四边网格离散极小曲面, 难度很大.因此, 本文拟采用优化算法, 由插值边界构造一张尽可能满足离散平均曲率处处为0的四边网格离散曲面.

为生成一张表面光滑的高质量离散极小曲面, 我们将文献[33]中的Laplacian算子推广到四边网格曲面, 并将其度量引入到待优化的目标函数之中.四边网格曲面在顶点v_i处的光滑性条件定义如下:

$ {v_i} = \frac{1}{{\left| {N({v_i})} \right|}}\sum\limits_{j \in N({v_i})} {{v_j}}, $

其中, N(v_i)为顶点N(v_i)的1-环邻域的顶点集合.由此, 我们可以定义四边网格曲面上的光滑性度量如下:

$ {J_{smooth}} = \frac{1}{2}{\sum\limits_k {\left\| {L{v_k}} \right\|} ^2}, $

其中, L=[L_{i, j}]为四边网格曲面上的Laplacian算子, 即

${L_{i, j}} = \left\{ \begin{array}{l} 1, {\rm{ }}i = j\\ - \frac{1}{{\left| {N({v_i})} \right|}}, {\rm{ }}j \in N({v_i})\\ 0, {\rm{ otherwise}} \end{array} \right.. $

需要说明的是, 上述拉普拉斯优化项的加入主要是为了生成比较光滑的空间网格曲面, 即需要对网格内部顶点的3个坐标分量x, y, z同时加以考虑, 这与平面网格生成阶段的拉普拉斯光顺过程并不重复:即网格生成阶段的拉普拉斯光滑处理是为了生成质量较好的平面四边网格, 进而得到比较理想的初始空间四边网格曲面; 而后一个拉普拉斯优化是为了在对面积极小相关的目标函数进行优化的同时, 保证空间离散网格极小曲面的光滑性.

由定义1, 构造与平均曲率度量相关的目标函数如下:

$ {J_{mean}} = \sum\limits_k {{{\left\| {H({P_k})} \right\|}^2}} . $

同理, 由定义2, 构造与面积度量相关的目标函数如下:

$ {J_{area}} = \sum\limits_k {A({E_k})}, $

其中, A(E_k)为网格单元E_k的面积.

综上, 本文所研究的四边网格离散极小曲面建模问题可归结为一个非线性优化问题:即由第3.4节中所构造的网格曲面M⁰作为初始解, 优化变量为其内部网格顶点, 优化函数为

$ \arg {\rm{ }}\mathop {\min }\limits_{{P_k}} {\rm{ }}{\omega _1}{J_{smooth}} + {\omega _2}{J_{mean}} + {\omega _3}{J_{area}} $

(5)

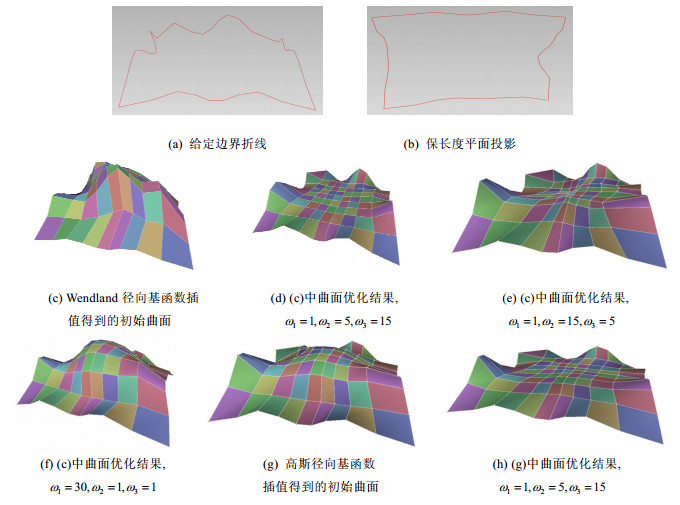
其中, w₁, w₂, w₃为加权系数.w₁越大, 所得到的网格曲面越接近拉普拉斯能量函数极小化结果; w₂越大, 所得到的四边网格曲面越接近平均曲率能量函数极小化结果; w₃越大, 所得到的四边网格曲面越接近面积函数极小化结果.为了使得最终的四边网格曲面模型既能尽量满足极小曲面条件又能具有较光滑的形状, 一般来说, 参数w₂和w₃的取值较大, 而参数w₁的取值较小.在本文的极小曲面造型实例中, 我们一般取w₁=1, w₂=5, w₃=15.给定同一初始曲面, 图 5(d)~图 5(f)中分别给出了选取不同的w₁, w₂和w₃时所得到的极小曲面优化结果.

对于优化问题(5), 本文通过拟牛顿非线性优化算法进行求解^[34].需要指出的是, 初始曲面M⁰对最终所得到的离散极小曲面形状具有一定的影响.为了说明初始构造对优化结果的影响, 图 5(g)中给出了采用高斯径向基函数方法构造的初始网格曲面, 图 5(h)给出了由该初始曲面得到的极小曲面优化结果, 其与由图 5(c)中的初始曲面优化得到的极小曲面(即如图 5(d)所示)具有不同的形状和面积值.

图 6和图 7分别给出了基于边界约束的四边网格离散极小曲面的若干建模实例.特别地, 图 7(c)给出了一个给定边界为两条封闭折线的例子.需要说明的是, 对于多条封闭折线的复杂情形, 我们将在以后的研究工作中继续讨论.

4 结论与将来的工作

离散极小曲面建模在建筑几何中具有重要的应用价值.基于我们提出的四边网格生成方法和径向基函数插值映射方法, 本文给出了由给定的一条封闭边界离散折线构造四边网格极小曲面的一般框架.通过该建模方法, 用户只需给定离散边界曲线, 便可自动生成具有优美形状和优良性质的四边网格, 可提高设计交互性, 并有望在玻璃结构及钢结构建模中得到应用.

如何找到目标函数中3个参数的最优选择, 是值得深入研究的一个问题.另外, 力学性能是建筑结构设计中需要考虑的重要因素.将来我们拟将最近新兴的等几何分析技术^[35]应用于极小曲面的建模问题, 以满足空间结构的力学性能要求.