2. ISN国家重点实验室(西安电子科技大学), 陕西 西安 710071
2. State Key Laboratory of Integrated Services Networks (Xidian University), Xi'an 710071, China
布尔可满足性问题(propositional satisfiability,简称SAT)是首个被证明的NP-Complete(NP-C or NPC)问题[1].给定一个布尔命题公式,SAT判定就是要找到一组变量的赋值使得该命题公式为真(即,该公式可满足),或者证明该命题公式不可能为真(即,该公式不可满足).SAT判定技术可以应用到人工智能规划(AI planning)、模型分析(model analysis)、定理证明、软件验证、电子设计自动化及验证等领域.近年来,SAT判定技术取得了很大的进展,研究人员开发了很多高效的SAT判定工具,进一步拓展了SAT判定的应用领域.在实际应用中,虽然基于SAT判定的方法并不一定是最好的,但与通过设计专门的工具来解决问题相比,将问题转换为SAT判定问题,利用现有的SAT判定工具来求解往往更为简单.
本文针对CNF(conjunctive normal form)公式的可满足性判定问题,目前,绝大部分SAT判定工具都要求输入是CNF形式,如果是其他形式的布尔公式,通过添加辅助变量,可以很容易地将其变换为CNF形式[2].
大部分SAT判定器采用的算法都是基于系统搜索的.在最坏情况下,系统搜索需要穷举所有变量的取值组合来判定公式的可满足性,判定算法的时间复杂度为O(2n),其中,n为公式中变量的个数.
虽然有大量的研究对判定技术做出了改进,但并不能改变SAT判定问题的指数复杂度属性.根据强指数时间复杂度猜想[3],一般SAT问题的判定复杂度为O(2εn),当问题规模趋于∞时,ε的值均趋近于1[4, 5].无论在理论上还是在实践中,都有很多SAT判定问题目前无法解决.
与已有的SAT判定技术相比,本文并不试图改进判定算法本身或者算法采用的数据结构来提高CNF公式的可满足性判效率,而是利用分治的思想,将复杂的CNF表示的SAT的判定问题划分为多个子问题来求解.方法的基本思路是:基于对CNF公式特点的分析,即:如果一个布尔公式F中的子句可以划分为m个子句组C1, C2,...,Cm,每个子句组中包含的变量集合分别为S1,S2,...,Sm,这些变量集两两不相交,即:对任意的1≤i≤m,1≤j≤m,i≠j,有Si∩Sj=∅,则布尔公式F是可满足的,当且仅当它的划分子句组C1,C2,...,Cm都是可满足的;布尔公式F是不可满足的,当且仅当它某个的划分子句组Ci(1≤i≤m)是不可满足的.
考虑采用穷举的方法来实现SAT判定的情形.如果将公式作为一个整体来判定,算法的时间复杂度为
O(2n),其中,n为公式中变量的总个数.利用划分的方法,上述的子句组的判定复杂度为$O({2^{|{s_1}|}} + {2^{|{s_2}|}} + ... + {2^{|{s_m}|}})$.考虑到n=|S1|+|S2|+...+|Sm|,直接进行判定时的复杂度为$O({2^n}) = O({2^{|{s_1}|}} \times {2^{|{s_2}|}} \times ... \times {2^{|{s_m}|}})$.可见,利用划分的判定方法会极大地降低判定的复杂度.
当然,很少有CNF公式能够直接产生子句组划分.为解决这一问题,本文提出了一种基于聚类的方法,先将子句聚类为多个簇,然后在公式中消去簇之间的公共变量,从而产生子句组划分.
子句组的可满足性判定,可以运用现有的SAT判定方法或者工具来求解.如果对每个子句组并行进行判定,对整个公式的判定时间将接近于单个子句组判定时间的最大值.
本文第1节介绍相关的研究工作.第2节给出相关的术语定义.第3节描述基于划分的SAT判定方法.第4节给出利用聚类来产生子句组划分的方法.第5节给出算法的实验结果.第6节对全文进行总结,并给出进一步的研究方向.
1 相关研究基于SAT解决问题的方法可以分为3个步骤,即:编码、预处理和SAT判定.编码是指通过某种形式的模型描述将问题用命题逻辑来表示,目前,大部分SAT判定工具都要求输入是CNF形式;预处理则是对原始公式进行某种形式的变换或化简,以减少经过预处理之后公式的可满足性判定时间.对公式的化简主要目的是减少公式中变量或者子句的个数,相关技术包括变量消除[6]和阻塞子句消除[7]等;SAT判定问题已经有了深入的研究,目前取得较好效果的SAT判定方法主要有两类,即:CDCL(conflict driven clause learning)方法和SLS(stochastic local search)方法[8].
大部分采用CDCL方法的SAT判定工具都是基于DPLL[9]的搜索方法.对于CNF形式的布尔公式,DPLL选定一个未赋值的变量,将其赋值为1(表示“真”)或者0(表示“假”),然后对公式运用隐含规则、单子句规则(unit clause rule)和布尔约束传播(Boolean constraint propagation,简称BCP)来进行推理.如果在某个步骤中发现存在某个子句的所有文字为假,则说明在当前赋值下公式不可能为真.这时需要通过回溯,尝试改变一些变量的赋值.和此前的方法相比,DPLL方法避免了原有的SAT判定算法的指数次方的空间复杂度问题,可以用于解决规模较小的实际问题.
GRASP[10]是第1个具有实用价值的SAT判定器,它主要在3个方面做出了改进,即:启发式决策、冲突驱动的学习和非时间序回溯.启发式决策是指在给变量赋值时,它总是选择能使最多的未确定值的子句为真的变量;冲突驱动的学习是指通过将当前产生冲突的信息编码成子句并添加到公式中,从而帮助减少未来的搜索空间;非时间序回溯是指当发现冲突需要回溯时,不是简单地回溯到最近的决策层,而是通过冲突分析来决定回溯的层次.GRASP可以处理包含1 000个左右变量的SAT判定问题.
zChaff[11]判定器实现了Chaff算法,Chaff算法的改进主要是两个方面,即:基于与变量状态无关的衰减和(variable state independent decaying sum,简称VSIDS)的启发式分支决策与基于两文字监视的布尔约束传播.在判定过程中,Chaff选择VSIDS值最大的文字对应的自由变量来进行分支决策,并对VSIDS值进行动态调整.由于VSIDS值与变量赋值无关,因此它的维护成本较小.两文字监视方法避免了每次对变量进行赋值时都要判断是否需要进行布尔约束传播的处理,并且在进行布尔约束传播时,只需要对监视文字被设为假的那些子句进行处理.zChaff可以处理包含10 000个左右变量的SAT判定问题.
BerkMin[12]主要在选择赋值变量和子句删除策略方面做了改进;MiniSat[13]则采用类似于Chaff算法,但在多个方面进行了调整.
Glucose[14]在MiniSat的基础上进行了改进.如果在冲突过程中学习得到的子句太多,将会影响到判定处理的效率.Glucose将这些学习得到的子句中的“坏子句”移除,以提高判定的效率.
此外,由于变量的决策顺序对于SAT的判定效率会产生很大的影响,因此,一些研究关注如何在预处理的过程中寻找较优的变量决策顺序,如文献[15]中提出一种方法,通过变量的活跃性、子句的连接性、变量在子句中的分布以及变量之间的关联来确定变量的决策顺序,以提高SAT判定的效率.
文献[16]提出用超图(hypergraph)划分的方法来加速布尔可满足性判定.将CNF公式中的子句看作顶点,将两个子句中的共同变量看作连接两个子句的边,可以将公式转换为一个超图.使用图的平衡二分法,可以将子句划分成两组,这两组子句间的共同变量称为割变量.如果把含有割变量的子句分出来,可以进一步得到第3个子句组.由于该文献采用的是平衡割的方法,因此得到的割变量个数往往很多,因此无法用消去变量的方法来将问题分解为独立的子问题求解,而只能是将割变量作为优先赋值的变量,通过调用其他判定工具来求解.另外,由于公式中子句的个数往往很多,因此图的分割也需要很长的时间.
SLS算法的基本处理过程是:首先给每个布尔变量设定一个初始值(一般是随机的),在接下来的每次处理中会选择一个变量,改变它的值.如此反复,直至发现使得布尔公式可满足的一种取值,或者是达到某种终止条件.近来,SLS算法也取得了很大的进展[17, 18, 19],尤其是对随机的SAT问题判定方面.
通过对判定算法和数据结构方面的改进,目前SAT判定工具可以解决大部分含有上万个变量的CNF公式的可满足性判定问题,但是由于问题本身的复杂性和实际应用(例如电子设计自动化)中问题规模的不断增大,目前的工具还远不能满足实际应用中的一些需要.
针对同一个SAT判定问题,由于不同的判定工具的效率不同,一种最直观、最简单的方法就是将同一SAT判定问题使用不同的判定工具,然后用并行或者分布式的方式来求解;然后,采用最先运行结束的判定工具的结果.如果使用随机判定工具,可以给判定工具设定不同的参数,如随机种子值.
也有一些研究尝试将问题划分为多个复杂度更小的子问题,然后用并行或分布式的方法来求解.例如,文献[20]中提出了一种基于划分的方法,该方法针对QBF(quantified Boolean formulas)公式的可满足性,根据公式中存在量词和全称量词的特点动态地将公式划分为多个子公式来求解.但该方法不能用于一般SAT问题的判定.
针对网格和云计算,文献[21]提出一种方法,递归地将SAT判定问题划分为子问题树,然后将树上的节点代表的子问题交给网络或者云,用并行的方式来进行判定.但该划分方法产生的子问题的判定复杂度与原问题的判定复杂度仍较为接近,就降低问题的复杂度而言,效果并不明显.
本文提出的方法是基于分治的思想,通过把CNF公式中的子句聚类到不同的簇,再消去簇之间的公共变量,产生子句组划分,从而将CNF公式的SAT判定问题转化为多个独立的子问题来求解.子问题的求解还可以并行,以进一步加快判定速度.
2 术语定义大部分SAT判定的相关工具开发和研究都限定了输入是CNF形式的公式,如果是其他形式的布尔公式,通过适当的转换方法,可以将公式转换为CNF形式.下面给出与CNF公式相关的一些定义.
定义1(文字l(literal)). 布尔变量的正或者负形式.
例如:对于布尔变量x,它对应的文字为x和¬x.
定义2(子句c(clause)). 一个或者多个文字的析取.
例如:(¬x1+x2+¬x3)就是一个子句.
定义3(CNF公式). 由一个或多个子句的合取构成的布尔公式.
例如:(¬x1+x2+¬x3)(x1+¬x2+¬x3)(x4+¬x5+¬x6)(¬x4+x5+¬x6)就是一个CNF形式的布尔公式.
定义4(子句组). CNF布尔公式中的一个或者多个子句合取构成子句组.
例如:(¬x1+x2+¬x3)(x1+¬x2+¬x3)和(x4+¬x5+¬x6)(¬x4+x5+¬x6)都是布尔公式(¬x1+x2+¬x3)(x1+¬x2+¬x3)(x4+ ¬x5+¬x6)(¬x4+x5+¬x6)的子句组.
定义5(子句组变量集). 一个子句中包含的文字对应的布尔变量的集合称为该子句的变量集.子句组中包含的所有子句的变量集的并称为该子句组的变量集.
例如:(¬x1+x2+¬x3)(x1+¬x2+¬x3)和(x4+¬x5+¬x6)(¬x4+x5+¬x6)对应的变量集分别为{x1,x2,x3}和{x4,x5,x6}.
定义6(子句组划分). 如果一个布尔公式可以分成多个子句组,且任意两个子句组的变量集的交集均为空,则称这些子句组构成该布尔公式的一个划分.
例如:子句组(¬x1+x2+¬x3)(x1+¬x2+¬x3)和子句组(x4+¬x5+¬x6)(¬x4+x5+¬x6)构成布尔公式(¬x1+x2+¬x3)(x1+ ¬x2+¬x3)(x4+¬x5+¬x6)(¬x4+x5+¬x6)的一个划分,但是子句组(¬x1+x2+¬x3)(x4+¬x5+¬x6)和子句组(x1+¬x2+¬x3) (¬x4+x5+¬x6)则不能构成布尔公式(¬x1+x2+¬x3)(x1+¬x2+¬x3)(x4+¬x5+¬x6)(¬x4+x5+¬x6)的划分.
3 基于划分的SAT判定 3.1 基本思想SAT判定问题是NPC问题,意味着这类问题的时间复杂度是指数次方的.如果问题的规模比较大,则SAT判定就很难.与现有SAT判定的研究不同的是,本文试图通过将复杂的CNF公式的SAT判定问题分解为多个子句组的SAT判定问题,以降低判定的复杂度.为了便于理解,先看前面提到的CNF公式:
| $(\neg {x_1} + {x_2} + \neg {x_3})({x_1} + \neg {x_2} + \neg {x_3})({x_4} + \neg {x_5} + \neg {x_6})(\neg {x_4} + {x_5} + \neg {x_6})$ | (1) |
如果使用传统的SAT判定方法,如果采用穷举的方法,需要考虑6个布尔变量的取值组合,也就是要考虑26种情形.但是如果我们把公式分为两个子公式,即:
| $(\neg {x_1} + {x_2} + \neg {x_3})({x_1} + \neg {x_2} + \neg {x_3})$ | (2) |
| $({x_4} + \neg {x_5} + \neg {x_6})(\neg {x_4} + {x_5} + \neg {x_6})$ | (3) |
直观来看:公式(1)是可满足的,当且仅当公式(2)和公式(3)都是可满足的.
对于公式(2),因为只有3个变量,所以判定公式(2)的可满足性在穷举的情况下只需要考虑23种情形.同样,对于公式(3),也只需要考虑23种情形.因此,当把公式(1)的判定问题转化为两个子公式的判定问题来求解后,只需要考虑23+23=24种情形.
就一般情况而言,假定一个布尔公式,它可以划分为m个子句组,即C1,C2,...,Cm,则此公式的判定问题可以转换为对子句组C1,C2,...,Cm分别进行判定来求解.
定理1. 如果一个布尔公式C可以划分为m个子句组C1,C2,...,Cm,每个子句组中包含的变量集合分别为S1,S2,...,Sm,对任意的1≤i≤m,1≤j≤m,i≠j,有S1∩S2=∅,则布尔公式C是可满足的,当且仅它的划分子句组C1,C2,...,Cm都是可满足的.
证明:
$ \bullet $ 先证明充分性:
如果C是可满足的,因为C=C1∧C2∧...∧Cm,故必然存在一组布尔变量的赋值,使得C1,C2,...,Cm都同时满足,因此,C1,C2,...,Cm都是可满足的.
如果C是不可满足,则必然存在某个子句组是不可满足的,故有子句组不都是可满足的.
$ \bullet $ 再证明必要性:
假定子句组C1,C2,...,Cm都是可满足的,则对于变量集合S1,S2,...,Sm,必然存在相应集合中的一组变量取值,使得C1,C2,...,Cm分别是可满足的.因为对任意的1≤i≤m,1≤j≤m,i≠j,有S1∩S2=∅,即:这些变量组中,变量的取值是不存在冲突的,故将这些变量组的取值合起来,就可以得到针对所有变量的一组取值,这组取值可以使C=C1∧ C2∧...∧Cm取值为真,从而有C是可满足的.
假定子句组C1,C2,...,Cm不都是可满足的,即:至少存在某个子句组Ci(1≤i≤m)的取值不可能为真,当然也不可能找到针对所有变量的一组取值,能使C=C1∧C2∧...∧Cm取值为真,从而有C是不可满足的.
3.2 基于划分的SAT判定方法如果一个CNF公式能够划分为多个子句组,则该CNF公式的可满足性判定可以转化为子句组的可满足性判定.因为子句组的规模小于原公式的规模,所以判定的复杂度会变低.
基于子句组划分的布尔可满足性判定方法的基本思路是:先将公式划分这子句组,然后对每个子句组分别进行可满足性判定:如果每个子句组都是可满足的,则原布尔公式是可满足的;如果存在某个子句组是不可满足的,则原布尔公式是不可满足的.
4 基于聚类的划分 4.1 基本思想在大部分情况下,可能无法直接产生布尔公式的子句组划分,本节提出了一种对布尔公式进行处理来产生布尔公式子句组划分的方法.为了便于理解,先看一个CNF形式的布尔公式:
| $(\neg {x_1} + {x_2} + \neg {x_3})({x_1} + \neg {x_2} + \neg {x_3})\left( {{x_2} + {x_3} + {x_4}} \right)\left( {{x_3} + {x_5} + {x_6}} \right)({x_5} + \neg {x_6} + \neg {x_7})(\neg {x_5} + {x_6} + \neg {x_7})$ | (4) |
这个公式没有办法直接划分为更小的子句组,但是如果我们考虑对x3进行赋值,采用一种类似于二叉决策的方法对公式进行化简,就可以产生子句组的划分:
$ \bullet $ x3取值为0时,公式化简为(x2+x4)(x5+x6)(x5+¬x6+¬x7)(¬x5+¬x6+¬x7),该公式可以划分为两个子句组,即:(x2+x4)和(x5+x6)(x5+¬x6+¬x7)(¬x5+¬x6+¬x7);
$ \bullet $ x3取值为1时,公式化简为(¬x1+x2)(x1+¬x2)(x5+¬x6+¬x7)(¬x5+¬x6+¬x7),可以进一步划分为两个子句组,即:(¬x1+x2)(x1+¬x2)和(x5+¬x6+¬x7)(¬x5+¬x6+¬x7).
直观地看,原公式不能直接产生子句组划分的原因,是因为有x3的存在,把整个公式中的子句联系在一起了.而通过赋值把x3从公式中消除后,这一联系不复存在,因而就可以产生子句组划分.
受此启发,我们认为:可以通过寻找能产生子句组划分的变量,然后通过这些变量来产生子句组划分.首先定义一个割变量(集)的概念,见定义7.
定义7(割变量(集)). 在CNF表示的布尔公式中,如果存在一个或者多个变量,当从公式中消除这些变量后,原本不能直接产生子句组划分的公式变成了可以产生子句组划分的公式,则这一个或者多个变量就称为割变量(集).
例如:对公式(4)而言,x3就是一个割变量,如果消去x3,该公式就可以产生子句组划分.
4.2 基于聚类的划分聚类(clustering)就是将数据分组成为多个簇(cluster)或类,使得在同一个簇内的对象之间具有较高的相似度,而属于不同簇之间的对象差别较大.聚类是数据挖掘、模式识别等研究方向的重要研究内容之一,在识别数据的内在结构方面具有极其重要的作用.
没有任何一种聚类算法或者技术可以普遍适用于各种类型数据集的聚类,这其中的原因之一就是因为很难给出簇的概念的精确定义[22].根据数据在聚类中的集聚规则以及应用这些规则的方法,可以将聚类算法大致划分为层次化的聚类算法(基于联接的聚类算法)、基于划分的聚类算法、基于密度和网格的聚类算法和其他聚类算法.
层次聚类又可以分为凝聚的层次聚类和分裂的层次聚类:
$ \bullet $ 凝聚的层次聚类采用自底向上的策略,首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有的对象都在一个簇中,或者某个终结条件被满足.绝大多数层次聚类方法属于这一类,它们只是在簇间相似度的定义上有所不同;
$ \bullet $ 与凝聚的层次聚类相反,分裂的层次聚类采用自顶向下的策略,它首先将所有对象置于同一个簇中,然后逐渐细分为越来越小的簇,直到每个对象自成一簇,或者达到了某个终止条件.
从上面的分析可以看出:要从一个CNF公式产生好的子句组划分,应该尽量减少不同的子句组之间的共同变量个数,也就是:应该将包含相同变量多的子句归到同一个子句组,将含共同变量少的子句归到不同的子句组.这样,才能降低消去这些变量所需的代价.
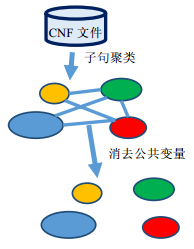
为此,本文提出了一种凝聚的层次聚类算法来实现这一目标.基本思想是:通过聚类将包含共同变量多的子句聚类到同一个簇中;然后,通过消去不同簇之间的共同变量来产生子句组划分.如图 1所示:算法先从文件中读出子句,把每个子句作为一个簇,然后用聚类方法将它们聚类到不同的簇(簇用圆圈表示)中,这些簇之间可能存在公共变量(用圆圈间的连线表示),将这些公共变量消去后,得到的簇就构成了原CNF公式的一种划分.
|
Fig.1 CNF 公式的聚类和划分 图 1 CNF clustering and partition |
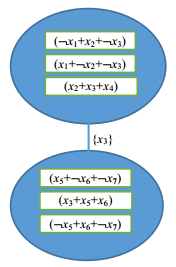
以公式(4)为例,由于子句(¬x1+x2+¬x3),(x1+¬x2+¬x3)和(x2+x3+x4)都包含变量x2和x3,因此将它们聚类到同一个簇.同样道理,将子句(x3+x5+x6),(x5+¬x6+¬x7)和(¬x5+x6+¬x7)聚类到同一个簇.消去两个簇之间的公共变量x3,就可以得到公式(4)的一种子句组划分.如图 2所示.
|
Fig.2 一个 CNF 公式的一种聚类 图 2 Clustering result of a CNF |
算法首先将每个子句作为一个簇,然后用层次聚类的办法来产生最终的聚类结果.为了记录簇中包含的子句和变量,簇定义为一个二元组,其中,clauseSet表示该簇包含的子句的集合,variableSet表示该簇包含的变量的集合.为简单起见,在下文中,簇Ci中包含的变量集将直接用Ci表示.
针对CNF表示的布尔公式的特点,两个簇C1和C2之间的相似度定义为:
定义8(簇之间的相似度):
$sim({C_1},{C_2}) = \max \left( {\frac{{|{C_1} \cap {C_2}|}}{{|{C_1}|}},\frac{{|{C_1} \cap {C_2}|}}{{|{C_2}|}}} \right),$
其中,|C1|,|C2|和|C1∩C2|分别表示簇C1,C2中变量的个数以及C1,C2中包含的变量集的交集中变量的个数.
子句组的聚类算法所算法1所示.算法中的3个输入DIMACS_file,min_cluster和threshold分别表示存储CNF公式的文件名(DIMACS格式[23])、期望的簇个数的最小值以及相似度阈值.为避免将所有子句聚类到一个簇,算法中用min_cluster来控制聚类结果中簇的个数:如果聚类后簇数结果小于min_cluster,则返回本次聚类之前的结果,即Cmin;否则,重复聚类过程.这是为了避免出现当threshold设置过小时,会将所有子句聚类成一个簇的情况.变量threshold决定两个簇之间的相似度大到什么程度时对两个簇进行合并:如果threshold设置得较大,则最终产生的簇的个数就会比较多,相应的割变量总个数也会增多;反之,如果threshold设置得较小,则簇的个数和割变量数也会相应地减少.
算法1. CNF_Clustering(DIMACS_file,min_cluster,threshold).
//通过聚类将子句划分到不同簇中
1. read clauses from DIMACS_file
2. create an empty cluster C
3. generate a cluster for every clause and added it into C
4. merged=true
5. loopUperBound=sizeof(C)
6. while merged do
7. merged=false
8. if sizeof(C)>min_cluster then
9. Cmin=C
10. else
11. break
12. end if
13. i=0
14. while (i<loopUperBound) do
15. j=0
16. max_similarity=0
17. max_index=i
18. while (i<loopUperBound) do
19. if i!=j then
20. $sim({C_i},{C_j}) = \max \left( {\frac{{|{C_i} \cap {C_j}|}}{{|{C_i}|}},\frac{{|{C_i} \cap {C_j}|}}{{|{C_j}|}}} \right)$
21. if sim(Ci,Cj)>max_similarity then
22. max_similarity=sim(Ci,Cj)
23. max_index=j
24. end if
25. end if
26. j=j+1
27. end while
28. if max_similarity≥threshold then
29. merge(Ci,Cmax_index)
30. merged=true
31. loopUperBound=loopUperBound-1
32. end if
33. i=i+1
34. end while
35. end while
36. if sizeof(C)>min_cluster then
37. return C
38. else
39. return Cmin
40. end if
4.3 算法的时间复杂度分析聚类算法的时间复杂度为O(c3),其中,c为公式中子句的个数.
对CNF公式进行聚类后,假定聚类结果包含划m个簇,每个簇中的子句包含的变量数分别为n1,n2,...,nm个,割变量的个数为k.因为需要分2k种情形将这k个变量消去,然后产生m个子句组分别进行判定,所以划分的时间复杂度为O(2k).
本文提出的算法主要针对k较小的情况,即,k小于某个特定的常数.在此情况下,聚类和划分的算法是多项式时间复杂度的.
如果子句组的判定采用穷举的方法,判定的总时间复杂度为$O({2^k} \cdot ({2^{{n_1}}} + {2^{{n_2}}} + ... + {2^{{n_m}}})),$其中,n1+n2+...+nm=n,n为原公式中变量的个数.
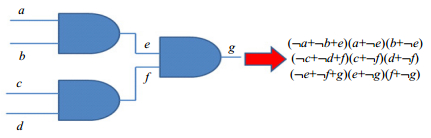
4.4 一个简单的实例给出聚类和划分方法应用的一个简单例子.假定要判定图 3中的电路是否是可满足,用SAT方法,可以先将电路转换为布尔公式,如图 3所示.
|
Fig.3 一个电路及其对应的布尔公式 图 3 A circuit and its corresponding CNF formula |
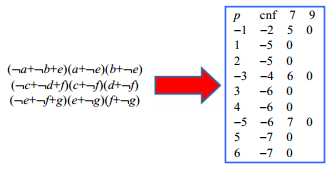
在SAT的研究领域,往往将布尔公式用CNF形式存储在文件中.将图 3中布尔公式中的变量(a,b,c,d,e,f,g)分别用数字1~7代替,并用负号代替取反符号,在每个子句后面加一个0作为子句的结束标志,文字之间用空格分隔,每个子句一行,并在文件的第1行加上子句数、变量数等信息,就得到了该公式对应的CNF文件,如图 4所示.
|
Fig.4 CNF 公式对应的文件存储形式 图 4 CNF formula and its file format |
如果将相似度定义为两个子句中的共同变量数与两个子句中包含的变量个数的比值中的较大者,对CNF文件中的子句进行聚类,可以将子句聚类成3个簇.消去簇间的共同变量,就可以将该公式划分为3个可以独立进行判定的子公式.这种划分相当于将电路划分成了3个子电路,如图 5所示.这一例子表明:通过聚类,可以从CNF公式中发现一些结构信息,利用这些结构信息,可以将复杂问题划分为相对简单的子问题.

|
Fig.5 布尔子句划分及其与电路对应关系 图 5 Relationship of CNF partition and circuit |
在电子设计自动化领域,往往通过先设计一些小的功能模块,再用这些小的功能模块来构建复杂的电路,各个电路模块之间的联系较少.在其他领域,如软件开发等,也大量存在这种情况.这意味着在很多情况下,可以将复杂的问题分解为多个子问题,且子问题之间相对独立.
4.5 对划分方法的改进在实现实验算法时,我们并未采用消去割变量的方法来产生子句组划分,因为这种做法在割变量数目较多时效率会很低.
为便于理解,以第4.1节中提到的公式(4)为例,通过聚类,将公式分成两个簇,即:(¬x1+x2+¬x3)(x1+¬x2+¬x3) (x2+x3+x4)和(x3+x5+x6)(x5+¬x6+¬x7)(¬x5+x6+¬x7),分别用C1,C2表示它们.对C1和C2分别进行可满足性判定:
$ \bullet $ 如果C1或C2是不可满足的,则公式(4)不可满足;
$ \bullet $ 如果C1和C2都是可满足的,且分别能找到使C1和C2都可满足的一组变量取值V1(x1,x2,x3,x4)和V2(x3,x5,x6,x7),其中,x3的取值不冲突(即,x3的取值都为0,或者都为1),则公式(4)是可满足的;否则,公式(4)是不可满足的.因为存在V1(0,0,0,1)和V2(0,1,1,0)能使C1和C2皆可满足,且x3的取值不冲突,故公式(4)是可满足的.
一般地,如果一个布尔公式C聚类为m个子句组C1,C2,...,Cm,为判定其可满足性,可以对每个子句组寻找使其满足的一组变量取值:
$ \bullet $ 如果C1,C2,...,Cm中的某个子句组是不可满足的,则公式不可满足;
$ \bullet $ 如果每个子句组都是可满足的,则判断使它们取值为真的变量值中割变量取值是否一致:
 若一致,则公式C是可满足的;
若一致,则公式C是可满足的;
 如果当前能使所有子句组都满足的变量取值中存在割变量取值冲突的情况,则寻找下一组能使C1,C2,...,Cm满足的变量取值;如果无法找到能使C1,C2,...,Cm为真,且割变量取值不冲突的变量取值组合,则公式C也是不可满足的.
如果当前能使所有子句组都满足的变量取值中存在割变量取值冲突的情况,则寻找下一组能使C1,C2,...,Cm满足的变量取值;如果无法找到能使C1,C2,...,Cm为真,且割变量取值不冲突的变量取值组合,则公式C也是不可满足的.
这一改进避免了穷举割变量的组合来消去割变量以产生子句组划分,且对现有的SAT判定工具稍加修改即可实现.
5 实 验针对SATLIB[24]和SAT Competition 2013中Application Benchmarks[25]的部分测试用例,用算法1进行聚类,得出的实验结果见表 1.在表 1和表 2中,省去了.cnf的扩展名,并且将过长的文件名使用其缩写表示.例如: bivium-39-200-0s0-0x5fa955de2b4f64d00226837d226c955de4566ce95f660180d7-30.cnf和bivium-39-200-0s0- 0x28df9231b320bd56dfb68bfc7c3f0ca20dbae6b0eba535ad91-98.cnf分别缩写为bivium-39-200-0s0-0x5f和bivium-39-200-0s0-0x28.
| Table 1 Results of CNF file clustering 表 1 CNF 文件聚类结果 |
实现中发现:如果相似度阈值大,则聚类后生成的簇数量可能就越多.为使实验结果更易理解,实验中将相似度阈值设得较小,使得最终产生的簇数量比较少.
表 1所示的实验结果表明:大多数测试用例都只需要消去较少的割变量甚至不用消去任何割变量,就可以将问题分解为几个子问题来求解span>.割变量总数为0,意味着聚类后可直接将原问题转化为规模更小的几个子问题来求进行判定.
表 2将直接运用SAT工具判定所用的时间和先用本文的提出的方法进行聚类后再运用SAT工具进行相应的处理判定所需的时间做了比较.实验上所用的SAT判定工具是lingeling[26],它在近年来的SAT Competition比赛中夺得了数个奖项.表 2中第1列表示待判定问题的文件名;第2列表示直接运用lingeling时所需的判定时间;第3列表示聚类所花的时间;第4列表示聚类处理后再用lingeling所花的判定时间,单位均为s.
| Table 2 Comparison of SAT solving 表 2 SAT 判定时间比较 |
从表 2中的实验结果可以看出:与直接SAT判定工具相比,在问题复杂度较低的情况下,由于本文提出的方法在聚类上花费的时间相对较多,因此相对而言需要花费更多的时间.但对于较为复杂的问题,即使算上聚类所用的时间,本文提出的方法还是可以大幅提高SAT判定的效率.运用本文提出的方法,绝大部分实验用例的判定都可以在较短时间内完成.
表 1中列出的有些文件由于判定所需时间太短而难以比较,因此在表 2中并未列出.有些问题虽然割变量总数为0,但聚类处理后判定速度提高并不明显,如Bivium-39-200-0s0-0x28.分析发现:这是由于聚类后很多簇中只包含一个变量的单子句,对于这些子句,SAT判定工具利用单子句规则就能直接处理,因此这一结果也在情理之中.
6 结 语在计算机科学领域,针对复杂问题,往往考虑采用分治法,将问题划分为多个规模更小的子问题来求解.本文正是基于分治的思想,通过将复杂的CNF表示的SAT的判定问题划分为多个子问题以降低判定的复杂度.提出了CNF形式的布尔公式的子句组划分的概念,并证明了布尔公式的可满足性问题可以转化为子句组的可满足性问题来求解.
给出了一种从CNF公式产生子句组划分以及利用子句组划分来进行SAT判定的方法.对于不能直接产生子句组划分的公式,提出了聚类的方法,将子句聚类成多个簇,把包含共同变量多的子句聚类到同一个簇,包含共同变量少的子句聚类到不同的簇,将不同簇之间的共同变量作为割变量,通过对每个簇单独判定,必要时再判断割变量的取值是否冲突,来判定公式的可满足性.
本文提出的方法主要有3个方面的优点:首先,利用子句组划分,可将问题分解为规模较小的子问题,从而降低SAT判定的复杂度;其次,由于每个子句组划分的判定可以并行,因而判定速度能得到进一步的提高;最后,由于此方法不涉及具体的SAT判定,因此,SAT判定技术的研究进展可以直接应用到对子句组划分的判定中.
因为本文提出的算法需要在聚类和判定割变量的取值是否冲突上消耗时间,因此如果对于简单的SAT判定问题,本文提出的算法可能比直接应用SAT判定算法要花费更多的时间代价;但是对于复杂的SAT问题,如果聚类后产生子句组划分所涉及的割变量个数较少,因此有可能大幅降低总的判定时间.
由于当前的聚类和划分工具只是一个初步的实现,相应的算法和工具都存在很大的改进空间.例如,实验所用的聚类和划分工具都是用Python语言来实现,而不是采用效率较高的C等语言,因此聚类处理用时较长也在预料之中.下一步将对聚类算法和工具进行改进,以大幅提高其运行速度,提高聚类质量.
此外,本文采用聚类的方法来产生子句组划分,实验中,相似度阈值选择是通过反复尝试来找到合适值的,目前我们还没有找到如何更好地确定相似度阈值的办法.此外,不同类型数据的簇的特征定义可能不同.因此,针对不同问题领域的CNF公式的聚类,可能需要不同的聚类算法,才能更好地利用问题本身的特征以获得最好的聚类效果.例如涉及逻辑电路的SAT判定,如果电路可以分成两个或者多个相对独立的子电路,就可以将这些子电路对应的CNF子句划分为相应的子句组.如何利用特定应用领域的知识来更好地产生子句组的划分,还需要进一步研究.
| [1] | Cook S. The complexity of theorem proving procedures. In: Proc. of the ACM SIGACT Symp. on the Theory of Computing. 1971 . |
| [2] | Tseitin. G. On the complexity of derivation in propositional calculus. In: Proc. of the Structures in Constructive Mathematics and Mathematical Logic, Part II: Seminars in Mathematics (translated from Russian). Steklov Mathematical Institute, 1968. 115-125 . |
| [3] | Impagliazzo R, Paturi R, Zane F. Which problems have strongly exponential complexity? Journal of Computer and System Sciences, 2001,63(4):512-530 . |
| [4] | Calabro C, Impagliazzo R, Paturi R. A duality between clause width and clause density for sat. In: Proc. of the 21st Annual IEEE Conf. on Computational Complexity. Washington: IEEE Computer Society, 2006. 252-260 . |
| [5] | Impagliazzo R, Paturi R. On the complexity of k-SAT. Journal of Computer and System Sciences, 2001,62(2):367-375 . |
| [6] | Eén N, Biere A. Effective preprocessing in SAT through variable and clause elimination. In: Proc. of the 8th Int’l Conf. on Theory and Applications of Satisfiability Testing (SAT 2005). LNCS 3569, 2005. 61-75 . |
| [7] | Järvisalo M, Biere A, Heule M. Simulating circuit-level simplifications on CNF. Journal of Automated Reasoning, 2012,49(4): 583-619 . |
| [8] | Biere A, Heule M, Maaren H, Walsh T, eds. Handbook of Satisfiability. IOS Press, 2009 . |
| [9] | Davis M, Logemann G, Loveland D. A machine program for theorem proving. Communications of the ACM, 1962,5(7):394-397 . |
| [10] | Marques-Silva J, Sakallah K. GRASP: A search algorithm for propositional satisfiability. IEEE Trans. on Computers, 1999,48(5): 506-521 . |
| [11] | Moskewicz M, Madigan C, Zhao Y, Zhang L, Malik S. Chaff: Engineering an efficient SAT solver. In: Proc. of the 38th Design Automation Conf. (DAC 2001). 2001. 530-535 . |
| [12] | Goldberg E, Novikov Y. Berkmin: A fast and robust SAT solver. In: Proc. of the 5th Design Automation and Test in Europe (DATE 2002). 2002. 142-149 . |
| [13] | Sörensson N, Eén N. MiniSat V1.13—A SAT solver with conflict-clause minimization. In: Proc. of the Posters of the Int’l Symp. on the Theory and Applications of Satisfiability Testing (SAT 2005). 2005. |
| [14] | Audemard G, Simon L. Predicting learnt clauses quality in modern SAT Solver. In: Proc. of the 21st Int’l Joint Conf. on Artificial Intelligence (IJCAI 2009). 2009. |
| [15] | Durairaj V, Kalla P. Guiding CNF-SAT search by analyzing constraint-variable dependencies and clause lengths. In: Proc. of the High-Level Design Validation and Test Workshop (HLDVT). 2006. 155-161 . |
| [16] | Durairaj V, Kalla P. Exploiting hypergraph partitioning for efficient Boolean satisfiability. In: Proc. of the 9th IEEE Int High Level Design Validation and Test Workshp. 2004 . |
| [17] | Cai SW, Su KL, Sattar A. Local search with edge weighting and configuration checking heuristics for minimum vertex cover. Artificial Intelligence, 2011,175(9-10):1672-1696 . |
| [18] | Cai SW, Su KL. Configuration checking with aspiration in local search for SAT. In: Proc. of the AAAI 2012. 2012. |
| [19] | Cai SW, Su KL. Local search for Boolean satisfiability with configuration checking and subscore. Artificial Intelligence, 2013,204: 75-98 . |
| [20] | Samulowitz H, Bacchus F. Dynamically partitioning for solving QBF. In: Proc. of the 10th Int’l Conf. on Theory and Applications of Satisfiability Testing (SAT 2007). 2007. 215-229 . |
| [21] | Hyvärinen A, Junttila T, Niemelä I. Partitioning SAT instances for distributed solving. In: Proc. of the Int’l Conf. on Logic for Programming, Artificial Intelligence, and Reasoning. LNCS 6397, 2010. 372-386 . |
| [22] | Estivill-Castro V. Why so many clustering algorithms? ACM SIGKDD Explorations Newsletter, 2002,4(1):65-75 . |
| [23] | CNF file format. 2013. http://people.sc.fsu.edu/~jburkardt/pdf/dimacs_cnf.pdf |
| [24] | Hoos H, Stützle T. SATLIB: An online resource for research on SAT. In: Gent IP, Maaren HV, Walsh T, eds. Proc. of the SAT 2000. IOS Press, 2000. 283-292. |
| [25] | sc13-Benchmarks-Application. 2013. http://www.satcompetition.org/2013/files/sc13-benchmarks-application.tgz |
| [26] | Biere A. Lingeling, plingeling and treengeling entering the SAT competition 2013. In: Balint A, Belov A, Heule M, Järvisalo M, eds. Proc. of the SAT Competition 2013. vol.B-2013-1 of Department of Computer Science Series of Publications B, University of Helsinki, 2013. 51-52. |
 2015, Vol. 26
2015, Vol. 26


