2. 中山大学 计算机软件研究所, 广东 广州 510275;
3. 中国电信股份有限公司 广东研究院, 广东 广州 510630
2. Software Institute, Sun Yet-San University, Guangzhou 510275, China;
3. Academy of Guangdong Telecom Company, China Telecom Corporation Limited, Guangzhou 510630, China
矩阵分解(matrix factorization,简称MF)是机器学习研究中最重要的工具之一,在协同过滤[1-5]、协作排序[6, 7]、社会网络分析[8]以及文本分析等领域都有广泛的应用.特别地,在以Netflix竞赛为代表的协同过滤问题的研究中,各种基于MF模型的实现都取得了很好的结果,显示了这一模型对解决大规模缺失数据的恢复问题的有效性.
在本文的工作中,我们考虑如下问题:考察由N个对象(记为o1,o2,…,oN)在T个连续时间点(记为t1,t2,…,tT)上生成的时间序列构成的矩阵R,其中,Ri,j对应对象oi在时间点tj上的取值,我们希望为R找到合适的因子矩阵U和V,使得$R \approx {U^T}V.$.
本文的工作在缺失数据的恢复研究中具有广泛的应用,如在交通数据采集系统中,为了采集各道路的通行速度数据,通常使用路面上探测车辆的行驶速度来估算道路的平均通行速度,但若有道路在某个时间点上没有探测车经过,则产生了数据缺失的现象,为填充这些数据,我们可以应用本文的工作,根据已采集获得的(不完整的)数据矩阵R拟合因子矩阵U和V,进而由乘积UTV得到对缺失速度值的估计;另一个潜在应用的例子是在某些药学实验中,为评估药物对患者的影响,一般需要根据预设的时间间隔多次从志愿者身上抽血检验其体内的血药浓度,为减少志愿者的痛苦和降低检测的费用,对每位志愿者,我们都可以为其随机选择若干时间点,并仅在这些时间点抽血检验,我们把这些采样获得的抽血数据构成矩阵R,进而可以使用与上述类似的方式,估算志愿者在其他时间点上的缺失的血药浓度.
对基于矩阵分解的缺失数据恢复研究,受Netflix竞赛的促进,在过去10年间已经有了极大的进展,但这些工作普遍隐含假设了数据的取值独立于外部环境的变化.而本文的目标矩阵R中数据则具有显著的时序特征,如在前文的例子中,城市道路在每一个时间点上的通行速度都与前一个时间点的速度相接近,志愿者服药后体内血药浓度在相邻时间点上的测量值也没有显著差异.这些观测结果提示我们在对类似的数据作矩阵分解时,应该把数据在时间轴上的演化效应也考虑在内.为描述数据的时序特征,在本文的工作中,我们首先提出一个适合于描述时序数据的概率图模型,在该模型中,提出使用两种不同的分布来描述时序数据中产生于相邻时间点上的数据间的联系;进而,将相应的导出两种不同的矩阵分解模型MAFTIS-I(matrix factorization for time series data-I)和MAFTIS-II;最后,将分别给出对MAFTIS-I,MAFTIS-II的求解策略.
本文第1节给出用到的主要记号的定义.第2节对矩阵分解的相关研究进行简要的总结.第3节提出面向时序数据的概率图模型,并将由其导出相应的矩阵分解模型和给出相应的求解策略.第4节将把本文模型分别应用于两个不同的数据集——标普500股票在一年内每天的开盘价格数据集和国内某城市交通路网上
1 853个路段在接近9 000个连续时间点上的通行速度数据一一进行恢复估计,以检验该模型的表现.最后是对全文工作的总结以及对未来工作的展望.
1 记 号
在本文中,若无特殊说明,所有向量均指列向量.对向量V=[v1,v2,…,vN]$ \in $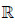 n,我们使用||V||0,||V||1和||V||2
n,我们使用||V||0,||V||1和||V||2
顺次表示V的0,1,2范数,其中,
● $||V|{|_0} = \sum\limits_{i = 1}^n {I({v_i} \ne 0)} $,即,V中非0分量的个数(这里,I(X)是指示函数,当X为真时,取值为1;否则为0);
● $||V|{|_1} = \sum\limits_{i = 1}^n {|{v_i}|} $;
● $||V|{|_2} = \sqrt {\sum\limits_{i = 1}^n {v_i^2} } $.
此外,对矩阵X$ \in $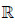 n×m,我们使用Xk表示X的第k列,并记X的Frobenius范数为$||X|{|_F} = \sqrt {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {X_{i,j}^2} } } $.
n×m,我们使用Xk表示X的第k列,并记X的Frobenius范数为$||X|{|_F} = \sqrt {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {X_{i,j}^2} } } $.
矩阵分解模型(也称为因子分解模型)的基本想法:对给定的原始矩阵R,寻求两个小规模因子矩阵U和V,使得因子矩阵的乘积可以近似地拟合R(即R$ \approx $UTV).一般的,这个分解可以由如下的最优化问题获得:
| $\{ U,V\} = \mathop {\arg }\limits_{U,V} \min Loss({U^T}V,R) + P(U,V)$ | (1) |
这里,U和V分别是d×M和d×N矩阵.为限制U和V的规模,通常有d<<min{M,N}.
Loss(UTV,R)是损失函数,用于刻画模型的经验误差,通常可以进一步分解为拟合矩阵中估计值(UTV)st与真实值Rst之间差异之和,即:
$Loss({U^T}V,R) = \sum\limits_{s = 1}^M {\sum\limits_{t = 1}^N {l({R_{i,j}},U_i^T{V_j})} } ,$
其中,函数l(x,y)一般取为平方误差损失(x-y)2[2-4,12,13,16-18]或绝对值误差损失|x-y|[5].
函数P(U,V)是惩罚因子,用于刻画模型本身的复杂度.在机器学习理论中,Vapnik提出使用最小描述长度(MDL)作为模型复杂度的通用度量[9],但事实上,MDL是不可计算的,因此在具体实现中,一般都使用其他度量代替.由于刻画矩阵复杂度的本质属性是它的秩(rank),所以P(U,V)的一个合适选择是rank(UTV)[10, 11],在Candes和Tao的研究中已经证明:在一定的稀疏性假设下,这一设置能够几乎无损的还原矩阵R[12, 13].但考虑到实际计算的问题,一种更为自然的选择是把P(U,V)取为U,V的Frobenius范数的平方和,即$(\alpha ||U||_{Fro}^2 + \beta ||V||_{Fro}^2)$.由Fazel[10, 11]与Srebro[5]的工作,当$\alpha = \beta = \frac{1}{2}$时,$(\alpha ||U||_{Fro}^2 + \beta ||V||_{Fro}^2)$与rank(UTV)的凸包络(convex envelope)相等,所以,这一选择可以看作是对rank(VTU)的凸近似.
注意到,公式(1)隐含假设了模型对缺失数据的恢复能力仅依赖于由它对已有数据的拟合能力,所以在本质上,这一模式是直推式的(transductive model)[9].众所周知,直推式模型虽然具有很多良好的性质(如算法的泛化性保证等[14]),但却不擅长对数据联系的刻画[5];另一方面,作为产生式模型(generative model)的典型代表,概率图模型[15]虽然能很容易地描述复杂的数据关系,但却难以为其泛化性提供理论保证.对此,Salakhutdinov及其合作者提出了概率矩阵分解模型(PMF)[3].PMF通过为U,V引入统计先验,实现了直推式模型与产生式模型两者的结合,并在Netflix缺失数据恢复问题上取得了成功.然而,PMF解决的主要是对数据内部特征间联系的刻画,但却未能进一步描述数据之间的依赖关系.为此,Salakhutdinov[16],Adams[17]和Pirreducible[18]等人都以类似的方式进行了尝试,他们引入了更高层次的先验(即超先验,hyperprior)来描述U,V的先验,从而实现了对数据间联系的表示.但这类模型的计算复杂度都相当高,所以只能应用于中小规模的问题求解[17];而对大规模的数据,则普遍需要使用抽样处理的策略[16, 18],因而求解效率不高.
3 面向时序数据的矩阵分解 3.1 模 型对由N个对象在T个连续时间点上产生的数据构成的矩阵R,为获得R的一个合适的分解R$ \approx $UTV,我们考虑图 1所示的概率图模型(MAFTIS).

|
Fig.1 The probabilistic graphical model of MAFTIS 图 1 MAFTIS的概率图模型 |
我们假设在图 1的各组成元素之间存在如下关系:
1) 矩阵U中的所有列向量都相互独立地服从于期望为0、协方差矩阵为$\sigma _U^2I$的高斯分布,即对于
1≤i≤N,有:
$\Pr ({U_i}|{\sigma _U}) = {(2\pi \sigma _U^2)^{ - \frac{d}{2}}}\exp \left\{ { - \frac{{||{U_i}||_2^2}}{{2\sigma _U^2}}} \right\}$;
2) 矩阵V中的所有列向量对于给定的先验$\sigma _V^2I$与$\zeta $构成马尔可夫随机场,即:
$\Pr (V|\sigma _V^2I,\zeta ) = \frac{1}{Z}\prod\limits_{i = 1}^T {\Pr ({V_i}|\sigma _V^2I,\zeta )} \times \prod\limits_{j = 2}^T P r({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta )$;
这里,$Z = \int {\prod\limits_{i = 1}^T {\Pr ({V_i}|\sigma _V^2I,\zeta )} } \times \prod\limits_{j = 2}^T {\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta ){\rm{d}}V} $是归一化因子.进一步地,对于1≤j≤T,我们设Vj服从均值为0、协方差矩阵为$\sigma _V^2I$的高斯分布,即:
$\Pr ({V_j}|\sigma _V^2I,\zeta ) = {(2\pi \sigma _V^2)^{ - \frac{d}{2}}}\exp \left\{ { - \frac{{||{V_j}||_2^2}}{{2\sigma _V^2}}} \right\}$.
此外,对于$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta )$,在后文的讨论中,我们分别考虑如下两种情形:
● 情形I:$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta ) = {\psi _1}({V_j} - {V_{j - 1}}|\zeta )$.这里,${\psi _1}\left( { \cdot \left| \zeta \right.} \right)$是均值为0的拉普拉斯(Laplace)分布,即:
$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta ) = {\psi _1}({V_j} - {V_{j - 1}}|\zeta ) = \frac{1}{{2\zeta }}\exp \left\{ { - \frac{{||{V_j} - {V_{j - 1}}|{|_1}}}{\zeta }} \right\}{\rm{ }}$;
● 情形II:$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta ) = {\psi _2}({V_j} - {V_{j - 1}}|\zeta )$.其中,${\psi _2}\left( { \cdot \left| \zeta \right.} \right)$是均值为0、协方差矩阵为${\zeta ^2}I$的高斯分布,即:
$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta ) = {\psi _1}({V_j} - {V_{j - 1}}|\zeta ) = {(2\pi {\zeta ^2})^{ - \frac{d}{2}}}\exp \left\{ { - \frac{{||{V_j} - {V_{j - 1}}||_2^2}}{{2{\zeta ^2}}}} \right\}$;
3) 矩阵R中的各成员Ri,j(1≤i≤N,1≤j≤T)分别独立地服从于期望为$U_i^T{V_j}$、方差为$\sigma _R^2$的正态分布,即:
$\Pr ({R_{i,j}}|U_i^T{V_j},\sigma _R^2) = {(2\pi \sigma _R^2)^{ - \frac{1}{2}}}\exp \left\{ { - \frac{{{{({R_{i,j}} - U_i^T{V_j})}^2}}}{{2\sigma _R^2}}} \right\}$.
下面我们根据图 1和上述的假设1)~假设3),对给定的矩阵R和参数${\sigma _U},{\sigma _V},{\sigma _R},\zeta ,$使用极大似然导出本文的矩阵分解模型.需要指出的是:在假设2)中,我们给出了两种可能的$\Pr ({V_j},{V_{j - 1}}|\sigma _V^2I,\zeta )$的分布,由于两者的推导过程类似,我们这里只针对情形I进行详细推导,对情形II我们将直接给出其主要结论.
在统计意义下,为R寻求合适的分解R$ \approx $UTV相当于最大化如下目标:
| $\{ U,V\} = \mathop {\arg }\limits_{U,V} \max \Pr (U,V|R,{\sigma _U},{\sigma _V},{\sigma _R},\zeta ){\rm{ }}$ | (2) |
由
| $\Pr (U,V|R,{\sigma _U},{\sigma _V},{\sigma _R},\zeta ) = \frac{{\Pr (U,V,R|{\sigma _U},{\sigma _V},{\sigma _R},\zeta )}}{{\Pr (R|{\sigma _U},{\sigma _V},{\sigma _R},\zeta )}}$ | (3) |
注意到,矩阵R和参数${\sigma _U},{\sigma _V},{\sigma _R},\zeta ,$均已给定,所以公式(3)中的分母Pr(R|${\sigma _U},{\sigma _V},{\sigma _R},\zeta ,$)可视为常数,则公式(2)等价于:
| $\{ U,V\} = \mathop {\arg }\limits_{U,V} \max \Pr (U,V,R|{\sigma _U},{\sigma _V},{\sigma _R},\zeta )$ | (4) |
由图 1和假设1)~假设3),我们有:
$\begin{array}{l} \Pr (R,U,V|{\sigma _U},{\sigma _V},{\sigma _R},\zeta ) = \Pr (R|U,V,{\sigma _U},{\sigma _V},{\sigma _R},\zeta ) \times \Pr (U,V|{\sigma _U},{\sigma _V},{\sigma _R},\zeta )\\ {\rm{ }} = \Pr (R|U,V,{\sigma _R}) \times \Pr (U|{\sigma _U}) \times \Pr (V|{\sigma _V},\zeta )\\ {\rm{ }} = \prod\limits_{i = 1}^N {\prod\limits_{j = 1}^T {\Pr ({R_{i,j}}|{U_i},{V_j},{\sigma _R})} } \times \prod\limits_{i = 1}^N {\Pr ({U_i}|{\sigma _U})} \times \prod\limits_{j = 1}^T {\Pr ({V_j}|{\sigma _V})} \times \prod\limits_{j = 2}^T {\Pr ({V_j},{V_{j - 1}}|\zeta )} \\ {\rm{ }} \propto \exp \left( { - \frac{1}{{2\sigma _R^2}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{(U_i^T{V_j} - {R_{i,j}})}^2}} } } \right) \times \exp \left( { - \frac{1}{{2\sigma _U^2}}\sum\limits_{i = 1}^T {||{U_i}|{|^2}} } \right) \times \\ {\rm{ }}\exp \left( { - \frac{1}{{2\sigma _V^2}}\sum\limits_{j = 1}^T {||{V_j}|{|^2}} } \right) \times \exp \left( { - \sum\limits_{j = 2}^T {\frac{{|{V_j} - {V_{j - 1}}|}}{\zeta }} } \right) \end{array}$.
对上式两端取对数,有:公式(4)$ \Leftrightarrow $
| $\{ U,V\} = \mathop {\arg }\limits_{U,V} \min \frac{1}{{\sigma _R^2}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{({R_{i,j}} - U_i^T{V_j})}^2}} } + \frac{1}{{\sigma _U^2}}\sum\limits_{i = 1}^N {||{U_i}||_2^2} + \frac{1}{{\sigma _V^2}}\sum\limits_{j = 1}^T {||{V_j}||_2^2} + \frac{1}{\zeta }\sum\limits_{j = 2}^T {||{V_j} - {V_{j - 1}}|{|_1}} $ | (5) |
我们令$\alpha = \frac{{\sigma _R^2}}{{\sigma _U^2}},\beta = \frac{{\sigma _R^2}}{{\sigma _V^2}},\lambda = \frac{1}{2}\frac{{\sigma _R^2}}{\zeta }$,则公式(5)可以等价写为模型(I):
| $\left. \begin{array}{l} \{ U,V\} = \mathop {\arg }\limits_{U,V} \min \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{({R_{i,j}} - U_i^T{V_j})}^2}} } + \frac{\alpha }{2}\sum\limits_{i = 1}^N {||{U_i}||_2^2} + \frac{\beta }{2}\sum\limits_{j = 1}^T {||{V_j}||_2^2} + \lambda \sum\limits_{j = 2}^T {||{V_j} - {V_{j - 1}}|{|_1}} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\alpha ,\beta ,\lambda \ge 0 \end{array} \right\}$ | (I) |
相应地,其优化目标称为目标(I).此外,与上述的过程完全类似,若我们采用假设2)中的情形II,我们可以得到以下的模型(II):
| $\left. \begin{array}{l} \{ U,V\} = \mathop {\arg }\limits_{U,V} \min \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{({R_{i,j}} - U_i^T{V_j})}^2}} } + \frac{\alpha }{2}\sum\limits_{i = 1}^N {||{U_i}||_2^2} + \frac{\beta }{2}\sum\limits_{j = 1}^T {||{V_j}||_2^2} + \frac{\lambda }{2}\sum\limits_{j = 2}^T {||{V_j} - {V_{j - 1}}||_2^2} \\ {\rm{s}}{\rm{.t}}{\rm{. }}\alpha ,\beta ,\lambda \ge 0 \end{array} \right\}$ | (II) |
以下给出模型(I)、模型(II)的性质的若干讨论:
首先,由目标函数的凸性和KKT条件[19],我们把模型(I)和模型(II)统一写为模型(III)):
| $\{ U,V\} = \mathop {\arg }\limits_{U,V} \min \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{({R_{i,j}} - U_i^T{V_j})}^2}} } $ | (III) |
s.t.
| ${\left| {\left| {{U_i}} \right|} \right|_2} \le A,i = 1,2, \ldots ,N$ | (C-1) |
| ${\left| {\left| {{V_j}} \right|} \right|_2} \le B,j = 1,2, \ldots ,T$ | (C-2) |
| $||{V_j}_{ + 1} - {V_j}|{|_q} \le C,j = 1,2, \ldots ,T$ | (C-3) |
其中,q=1或2,A,B,C是预设常数,分别与α,β和λ这3个约束系数相对应:约束系数越大,则相应常数的取值越小;否则反之.
由模型(III)中的约束(C-1)~(C-3)可以看出:在本文的模型中,因子矩阵U和V的地位是不对称的,我们称U为(潜在的)局部对象特征矩阵,U1,U2,…,UN分别对应数据对象o1,o2,…,oN的静态描述;称V为(潜在的)全局环境特征矩阵,V1,V2,…,VT对应了由o1,o2,…,oN所共享的外部环境在时间点t1,t2,…,tT上的取值.因此,在MAFTIS的表示下,矩阵R可以看作是由静态的对象特征与动态的环境特征共同作用的结果.如在城市的交通系统中,R对应了由各道路在不同时间点上的通行速度构成的矩阵,它可以认为是静态的道路特征与时变的环境特征两者的合成.这里的道路特征可能是道路等级、车道数目以及路面平整状况等因素,对所有道路的特征描述构成了因子矩阵U;另一方面,注意到同一城市内所有道路都共享同样的动态外部环境,如天气状况、能见度、城市人口的生活与工作规律等,对所有时间点上的这些因素的刻画则构成了矩阵V.
由时序系统在时间上的连续性,对两个相邻的时间点tj-1和tj(2≤j≤T),当它们之间的间隔充分小时,各数据对象在这两个点上产生的数据应接近相等,即:若|tj-tj-1|$ \to $0,则在2范数意义下,应有:
$|{R_j} - {R_j}_{ - 1}|{|_2} \to 0.$
对于这一行为,约束(C-3)为其提供了保证:
由
$||{R_j} - {R_j}_{ - 1}\left| {\left| {_2 = } \right|} \right|{U^T}{V_j} - {U^T}{V_j}_{ - 1}|{|_2} \le {\left| {\left| U \right|} \right|_2}||{V_j} - {V_j}_{ - 1}|{|_2},$,
注意到:
$||U|{|_2} \le ||U|{|_F} \le \sum\limits_{i = 1}^N {||{U_i}|{|_2}} \le N \times A.$
当q=2时,令C$ \to $0,即有:
$|{R_j} - {R_j}_{ - 1}|{|_2} \le N \times A \times C \to 0;$;
对q=1,由于
$|{V_j} - {V_j}_{ - 1}|{|_2} \le ||{V_j} - {V_j}_{ - 1}|{|_1} \le C,$,
因此,同样地令C$ \to $0,我们仍然可以得到||Rj-Rj-1||2$ \to $0.
现对模型(I)和模型(II)两者进行对比讨论.虽然通过调节约束(C-3)中C的取值(或者相应地,调节模型(I)和模型(II)中的λ值),我们都可以获得MAFTIS在时间上的连续性(即,对|tj-tj-1|$ \to $0,我们可以保证||Rj-Rj-1||2$ \to $0),然而模型(I)和模型(II)两者之间仍然有实质性的区别:我们考虑当相邻时间点tj-1和tj充分接近时,对全局的环境对象而言,不仅其在tj-1和tj这两个时间点上的特征变化幅度趋向于0,而且环境对象自身发生改变的属性的数目也将趋向于0.对于前者,我们可以使用1范数||Vj-Vj-1||1或2范数||Vj-Vj-1||2度量;而对于后者,其精确的取值为||Vj-Vj-1||0,由于0范数的离散性,使其难以适用于大规模的计算.而另一方面,根据Candes和Tao的结果[20],在一定条件下,||X||0与||X||1等价.除此之外,由||X||2≤||X||1,所以对于模型(III),在保持A,B和C的取值不变的情况下,由q=1,我们可以获得比q=2更强的表达能力.
3.2 模型求解本节讨论对MAFTIS的求解,为方便讨论,我们把模型(I)和模型(II)的优化目标合并为如下表达式:
| $S = \mathop {\arg }\limits_{U,V} \min \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^T {{{({R_{i,j}} - U_i^T{V_j})}^2}} } + \frac{\alpha }{2}\sum\limits_{i = 1}^N {||{U_i}||_2^2} + \frac{\beta }{2}\sum\limits_{j = 1}^T {||{V_j}||_2^2} + \frac{\lambda }{q}\sum\limits_{j = 2}^T {||{V_j} - {V_{j - 1}}||_q^q} $ | (6) |
这里,q=1或q=2.
由于S对Ui(i=1,2,…,N)和Vj(j=1,2,…,T)分别为凸,因此我们可以使用交替梯度下降[21]对上式求解.
记S对Ui的偏导为$\frac{{\partial S}}{{\partial {U_i}}}$,对Vj的偏导为$\frac{{\partial S}}{{\partial {V_j}}}$,在表 1中,我们给出了基于公式(6)的矩阵拟合算法.
| Table 1 The fitting algorithm 表 1 拟合算法 |
在表 1的计算流程中,其核心步骤是对梯度$\frac{{\partial S}}{{\partial {U_i}}}$和$\frac{{\partial S}}{{\partial {V_j}}}$的计算,下面我们分别对此展开讨论.
容易看出,无论q=1或q=2,$\frac{{\partial S}}{{\partial {U_i}}}$可使用下式计算:
$\frac{{\partial S}}{{\partial {U_i}}} = - \sum\limits_{j = 1}^T {({R_{i,j}} - U_i^T{V_j})} {V_j} + \alpha {U_i}$.
下面计算$\frac{{\partial S}}{{\partial {V_j}}}$.
我们先考察q=1的情形,此时,$||{V_j} - {V_{j - 1}}||_q^q = ||{V_j} - {V_{j - 1}}|{|_1}$.注意到函数||X||1在0点不可导,因而需要考虑使用次梯度(subgradient)或其他近似方法.对于前者,注意到在给定因子矩阵U的前提下,公式(6)具有与Fused Lasso模型[22]相接近的形式,所以一个自然的考虑方向是引入与Fused Lasso相类似的解决策略,如基于路径的交替优化模型[23].然而,由于公式(6)对系数向量Vj使用了2范数惩罚($||{V_j}||_2^2$),这使得文献[23]中的一个依赖于1范数惩罚的关键结论——软阈值调节(soft thresholding),不能适用于本文的问题;另一方面,该文提出的交替下降-系数融合(descent-fusion)的策略仍然需要较高的计算代价,因而也不适用于大规模计算的场景.
在本文的工作中,我们考虑如下的近似计算策略:对X$ \in $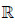 1,我们定义||X||1的基于2范数的$\tau $近似为
1,我们定义||X||1的基于2范数的$\tau $近似为
$||X|{|_{2~\tau }} = \sqrt {{X^2} + \tau } \approx ||X|{|_1},$
其中,$\tau $>0,是一个充分小的预定义常数,这里我们取为X的精度的$\frac{1}{{100}}$.
进一步地,对向量X=[x1,x2,…,xl]$ \in $,我们定义:
$||X|{|_{2~\tau }} = [\sqrt {x_1^2 + \tau } ,\sqrt {x_1^2 + \tau } ,...,\sqrt {x_l^2 + \tau } ]' \approx ||X|{|_1}.$
我们在图 2中展示了当X$ \in $[-1,1]时,在步长为0.05,$\tau $=0.0001的设置下,||X||2~$\tau $对||X||1的近似效果,其中,由符号o构成的虚线对应函数Y=|X|,由‘+’构成的虚线对应了Y=||X||2~$\tau $.此外,作为对比,我们也使用连续实线表示了函数Y=X2的曲线.

|
Fig.2 The approximation effects to ||X||2~$\tau $ by ||X||2 and ||X||1 respectively 图 2 ||X||2~$\tau $与||X||2对||X||1的近似效果 |
从图 2可以看出,函数Y=||X||2~$\tau $与函数Y=|X|两者的曲线几乎完全重合.因而可以预期:当公式(6)中q=1时,范数||X||2~$\tau $与||X||1也具有相近的约束能力.
以下我们把公式(6)中的各||·||1项都使用为相应的||·||2~$\tau $近似,进而对1≤j≤T计算$\frac{{\partial S}}{{\partial {V_j}}}$.
为简化表述,我们记${G_j} = - \sum\limits_{i = 1}^N {({R_{i,j}} - U_i^T{V_j})} {U_i} + \beta {V_j}$,则:
● 对于j=1,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} + \lambda {\left[ { - \frac{{{V_{1,j + 1}} - {V_{1,j}}}}{{\sqrt {{{({V_{1,j + 1}} - {V_{1,j}})}^2} + \tau } }},..., - \frac{{{V_{d,j + 1}} - {V_{d,j}}}}{{\sqrt {{{({V_{d,j + 1}} - {V_{d,j}})}^2} + \tau } }}} \right]^\prime }$;
● 对于1<j<T,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} + \lambda {\left[ {\frac{{{V_{1,j}} - {V_{1,j - 1}}}}{{\sqrt {{{({V_{1,j}} - {V_{1,j - 1}})}^2} + \tau } }} - \frac{{{V_{1,j + 1}} - {V_{1,j}}}}{{\sqrt {{{({V_{1,j + 1}} - {V_{1,j}})}^2} + \tau } }},...,\frac{{{V_{d,j}} - {V_{d,j - 1}}}}{{\sqrt {{{({V_{d,j}} - {V_{d,j - 1}})}^2} + \tau } }} - \frac{{{V_{d,j + 1}} - {V_{d,j}}}}{{\sqrt {{{({V_{d,j + 1}} - {V_{d,j}})}^2} + \tau } }}} \right]^\prime }$;
● 对于j=T,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} + \lambda {\left[ {\frac{{{V_{1,j}} - {V_{1,j - 1}}}}{{\sqrt {{{({V_{1,j}} - {V_{1,j - 1}})}^2} + \tau } }},...,\frac{{{V_{d,j}} - {V_{d,j - 1}}}}{{\sqrt {{{({V_{d,j}} - {V_{d,j - 1}})}^2} + \tau } }}} \right]^\prime }$.
以下计算q=2的情形.我们对Gj的定义同上,根据公式(6),我们直接有如下结果:
● 对于j=1,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} - \lambda ({V_{j + 1}} - {V_j})$;
● 对于1<j<T,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} + \lambda (2{V_j} - {V_{j - 1}} - {V_{j + 1}})$;
● 对于j=T,有:
$\frac{{\partial S}}{{\partial {V_j}}} = {G_j} + \lambda ({V_j} - {V_{j - 1}})$.
另外,对于表 1算法的具体实现,我们还有如下内容的需要注意:
首先,为简化参数的调节,在算法中,我们令$\eta $1=$\eta $2,并取α=β,α与λ的具体取值使用网格搜索策略确定;
其次,表 1算法的另一个关键问题是对因子矩阵的特征维度d的确定,对此,我们首先引述如下结论[24]:
对矩阵R$ \in $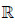 N×T的一个奇异值分解R=UTΣV,其中,U=[u1,u2,…,uN]$ \in $
N×T的一个奇异值分解R=UTΣV,其中,U=[u1,u2,…,uN]$ \in $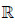 N×N且UUT=IN,V=[v1,v2,…,vT]$ \in $
N×N且UUT=IN,V=[v1,v2,…,vT]$ \in $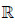 T×T且VVT=IT,Σ=diag($\sigma $1,$\sigma $2,…,$\sigma $min{N,T})$ \in $
T×T且VVT=IT,Σ=diag($\sigma $1,$\sigma $2,…,$\sigma $min{N,T})$ \in $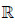 N×T且$\sigma $1≥$\sigma $2≥…≥$\sigma $min{N,T},则对R的任意秩数为k的近似Rk,有:
N×T且$\sigma $1≥$\sigma $2≥…≥$\sigma $min{N,T},则对R的任意秩数为k的近似Rk,有:
$||R - {R_k}|{|_2} \ge \sum\limits_{i = 1}^k {{\sigma _i}{u_i}v_i^T} = {\sigma _{k + 1}}$.
上述结果显示:当R中不包含缺失元素时,我们可以根据对R的奇异值分解结果和拟合精度的需要选择合适的d值.然而当R是不完整的矩阵时,由于诸$\sigma $的取值无法提前获得,因而也难以根据精度的需要确定合适的d值.对此,一般地,我们只能以经验的方式选取,即:在实验中调节不同的d值,并根据实验结果确定其最终的取值.
4 实 验 4.1 实验设置● 实验数据
我们把本文算法分别应用于两个不同领域的缺失数据恢复问题中以检验其表现,其中,第1个数据集是标普500数据集(以下称为stock数据集),它使用524(行)×245(列)的矩阵R来记录2009年8月21日~2010年8月20日间用于计算标准普尔500指数的524个组成股票在连续245个交易日的开盘价格数据(在此期间,共有524个股票被选入了标普500指数的计算);第2个数据集是城市路网的历史交通速度数据集,它使用1853(行)×8729(列)的矩阵R记录了某城市在连续30天内以GPS浮动车技术采集获得的市内1 853个路段上的平均通行速度数据.这里,R中的每行对应一个路段,每列对应一个采集时间点,任意两个时间点之间的时间间隔固定为5分钟.若路段i在时间点j上有浮动车经过,则把Ri,j记为在此时间间隔内路段i上所有浮动车速度的平均值;否则,记Ri,j为空.由于城市内的浮动车数目远小于路段的数目,因而R中有大量的数据缺失.事实上,R中的元素总数目约为1 600万,而其中非空元素却不到800万个,仅占总数的50%.
为分析这些数据在时间轴上的变化特点,首先给出数据增长率(rate of increment,简称roi)的计算定义.
给定x,y$ \in $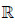 ,定义:
,定义:
| $roi(x,y) = \frac{{y - x + c}}{{x + c}}$ | (7) |
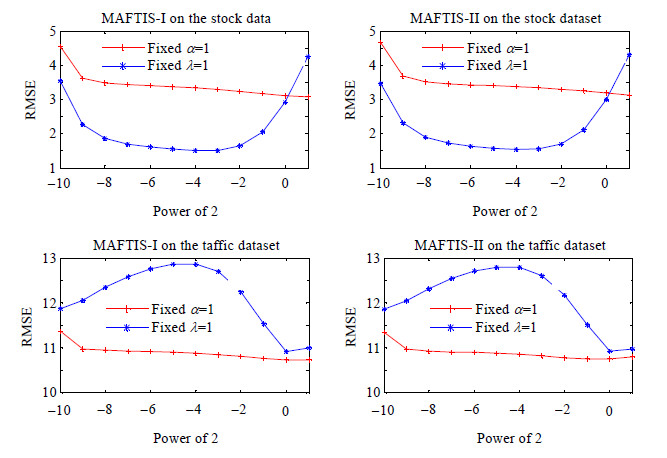
其中,c$ \in $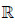 +,是一个充分小的常量,用以避免出现分母为0的情形.
+,是一个充分小的常量,用以避免出现分母为0的情形.
根据上述定义,我们称roi(x,y)为y相对于x的增长率.
令c=0.001,根据公式(7)分别计算了stock和traffic数据集中各数据对象在相邻时间片上后者相对于前者的数据增长率(即:对每一个矩阵R,我们都计算了所有的roi(Ri,j-1,Ri,j),这里,1≤i≤N且2≤j≤T).我们拟合了这些数据增长率的累积密度分布(cumulative density distribution,简称CDF),其结果如图 3所示.
|
Fig.3 The cdfs of the roi values of the data 图 3 Stock与traffic数据的roi值累积密度分布 |
图 3左边的子图对应了stock数据集,右边的子图对应了traffic数据集.为方便对比,我们在两个子图中都同时以虚直线标注了x=0的位置.由图 3可以看出,stock中各股票每天的开盘价格相对于前一天的增长率都集中在一个非常窄的区间[-10%,10%]之内.这一现象表明:所有股票每天的开盘价格都以前一天的价格为中心,并相对于此价格仅作轻微的波动,从而所有股票在整个时间段上的开盘价格呈现的是渐变的形式.而另一方面,有别于stock中的数据,traffic中各路段通行速度的变化更多的以“突变”的方式出现:在两个相邻时间点之间,增长率在[-10%,10%]间的数据仅占了全体数据的30%左右,而其他数据的变化幅度则非常大,后一时间点上的路段通行速度既有可能突然降低至0,也有可能上升到前一时间点的十数倍.由此可以认为:在traffic数据集中,各路段在不同时间点上的通行速度是以接近相互独立的方式发生变化的.对于这一现象,我们猜测主要由城市交通自身的特点所决定,由于城市内道路的交通灯较多并且状态转换频密,因此即使对同一路段,它在相邻时间点上的通行速度可能会存在显著的差异.
● 测试协议
对每个数据集,我们在实验中都采用了Given X协议[25]对算法进行评估,这里,X是算法中所使用的训练数据占总体观测数据的比例,余下的数据则作为测试数据用于算法评估.
算法的准确度采用根方平均误差(root mean square error,简称RMSE)度量,即:
$RMSE = \sqrt {\frac{1}{{|\Gamma |}}\sum\limits_{{R_{i,j}} \in \Gamma } {{{({R_{i,j}} - \widehat {{R_{i,j}}})}^2}} } $.
这里,$\Gamma $是测试数据的集合,$\widehat {{R_{i,j}}}$是对$\Gamma $中数据Ri,j的估计.
● 基准算法
我们选择概率主成分分析(PPCA)[26]和概率矩阵分解(PMF)[3]作为与本文算法对比的基准算法,其中,前者在交通流缺失数据的恢复研究中获得了非常好的结果[27],后者是在Netflix数据集上表现最好的矩阵恢复算法之一.本文实验中的PPCA使用了文献[28]的实现,PMF则采用了文献[29]的实现.
4.2 实验结果本节用于汇报MAFTIS在测试数据集上的结果,包括参数调节对MAFTIS的性能的影响、因子矩阵U,V的内部结构分析、MAFTIS在矩阵缺失数据恢复上的表现和MAFTIS的收敛速度分析.由于stock和traffic中的数据在时间轴上的演化模式迥异,所以我们同时汇报了MAFTIS在这两个数据集上的运行结果.
● 参数调节
我们先检验对因子α(注意到:在我们的实验设置中,有α=β)和λ的调节对MAFTIS的性能影响.我们分别以一致采样的方式从stock和traffic两个数据集上抽取了50%的数据作为测试集,余下的50%作为训练集,并在MAFTIS中分别以固定α、改变λ和固定λ、改变α这两种方式进行数据恢复.在实验中,我们分别把α和λ两者之一固定为1,另一个则逐步取值为2-10,2-9,…,20,21,实验结果如图 4所示.
|
Fig.4 The completion results by MAFTIS with different parameter settings 图 4 MAFTIS在不同参数设置下的数据恢复结果 |
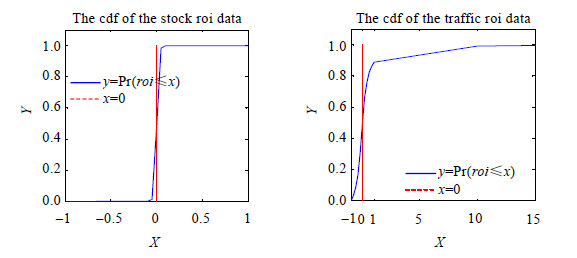
图 4上面一行是MAFTIS在stock数据集上的数据恢复结果,下一行是在traffic数据集上的结果;图中的左列对应模型(I),右列对应模型(II).各图的横坐标对应2的幂次,纵坐标对应在(α,λ)参数设置下的RMSE值,由‘+’构成的折线对应固定α=1,改变λ得到的结果;由‘*’构成的折线则对应了固定λ=1,改变α得到的结果.
从图 4可以看到,模型(I)、模型(II)在相同数据集上的走势几乎完全一致.特别地,在固定α的情况下(对应图中的‘+’折线),我们可以看到,公式(6)中的约束项$\frac{\lambda }{q}\sum\limits_{j = 2}^T {||{V_j} - {V_{j - 1}}||_q^q} $对预测结果具有显著的影响:在图 4的4个子图中,RMSE都随着λ的增长稳步降低.值得强调的是:在所有实验的最后(λ=2),我们所获得的预测误差与λ取初值(λ=2-10$ \approx $0.001,此时约束项的影响接近于0)时相比都有了大幅度的降低.
我们对图 4结果的另一个有趣发现是:在两个数据集上,预测误差随着α的变化显示出了截然相反的行为:在stock数据集上,α越大,则RMSE越小;在traffic数据集上,RMSE却随着α的增大而增大.事实上,这一现象可以通过对比假设1)~假设3)与公式(6)得到很好的解释:我们固定$\sigma _R^2$为常数,则有$\alpha \propto \frac{1}{{\sigma _U^2}},\beta \propto \frac{1}{{\sigma _V^2}}$.注意到: stock中的数据是以“渐变”的行为发生变化的,因而其总体方差$\sigma _V^2$较小,相应的β应取较大的值;而traffic中的数据则以“突变”的行为为主,变化较为激烈,所以其方差$\sigma _V^2$较大,相应的β的取值应偏小.由于在我们的实现中,为方便参数调节,我们强制规定了α=β,所以图 4的现象正是对以上结果的合理反映.
另外,还需指出的是:图 4显示,在所有情况下,预测误差都稳定的随λ的增加而缩小,因而我们可以通过指数序列2-10,2-9,…,20,21,…,2n,…快速确定λ的取值.对于α(=β),在stock数据集上,其预测误差的“谷底”所对应的α的取值区间约为[2-7,2-2];而在traffic数据集上,其预测误差自α≥2-4开始表现出快速下降的趋势,因而α参数的经验最优值也可以通过为其构造2的指数序列调节获得.
● 数据恢复结果
下面比较在不同的数据缺失程度下,应用MAFTIS-I(q=1),MAFTIS-II(q=2)及基准算法对stock和traffic作数据恢复的效果.对每一个算法,它在每一个数据集上的所有实验都使用相同的参数设置.特别地,对于本文所提出的MAFTIS-I和MAFTIS-II,两者的参数设置完全一致:在stock数据集上,α=β=2-4,λ=2.5;在traffic数据集上,α=β=1,λ=2.5.另外,对于参与实验的其他基准算法,其参数也以上一节参数调节的方式,通过网格搜索确定.
在Given X协议中,我们把X从10%开始,按10%的步长顺次取到90%,在stock数据集上的实验结果汇总在表 2中,在traffic数据集上的结果汇总在表 3中(结果越小越好).
| Table 2 Results on the stock dataset (smaller is better) 表 2 在stock数据集上的实验结果(结果越小越好) |
| 表 3 在traffic数据集上的实验结果(结果越小越好) Table 3 Results on the traffic dataset (smaller is better) |
从表 2、表 3可以看出:除在d=10且Given 80%这一设置下由PMF在stock数据集上获得最小的预测误差外,MAFTIS在其他所有实验中对基准算法都有显著的优势.特别地,在stock数据集上,MAFTIS-II在几乎所有情况下都取得了最好的表现;而在traffic数据集上,MAFTIS-I的优势则更为明显.这启发我们,MAFTIS-I,MAFTIS- II各有其适用范围:当数据间的变化以渐变方式发生时,MAFTIS-II可能较为合适;若数据间的变化以突变为主时,则MAFTIS-I可能会有更好的结果.
我们还注意到,在stock和traffic数据集上,调节维度参数d对结果的影响也不尽相同:在stock数据集上,当d值由10上升至30时,除PMF外,其他3个算法实现的预测误差都有明显的降低;然而在traffic数据集上,这一改变对结果却近乎没有发生影响.对此,我们猜测可能与数据集自身的性质有关:城市交通的实时运行虽然有很大的不确定性,然而总体上却有其周期性,这一宏观规律决定了traffic数据集的基空间组成仅需包含少量(≤10)的基向量;而对stock数据,由于证券市场变化的周期性并不明显,因而其基空间也需要更多的组成向量,所以当我们提高d的取值时,预测结果的质量也相应得到提升.
● 因子矩阵分析
正如我们在前文的讨论中所指出的:MAFTIS中的矩阵U刻画了(独立同分布的)局部数据对象的静态特征, V则刻画了作用于全局的环境对象在时间上的动态特征.作为对这一结果的直接反映,U,V内部各相邻列向量之间的差值应有不同的表现:对于U,由于各列对应的数据对象相互独立,所以相邻列向量之差的分布也没有明显的规律性;而V对应了各数据对象在时间轴上的动态行为,因而其内部数据应与R具有相同的变化趋势.
为度量V中列向量间的变化幅度,我们把向量Y相对于X的变化率(rate of change)记为roc(X,Y),其计算方式定义为
| $roc(X,Y) = \frac{{||Y - X|{|_2}}}{{||X|{|_2}}}$ | (8) |
数据恢复实验中,以Given 50%设置下获得的因子矩阵为例,分析U,V各自的性质.
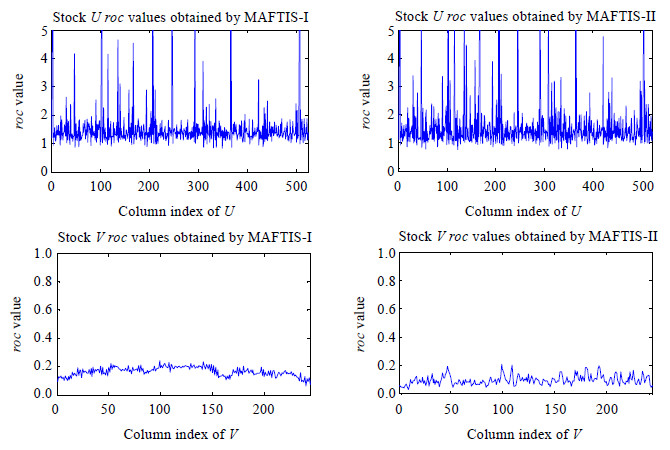
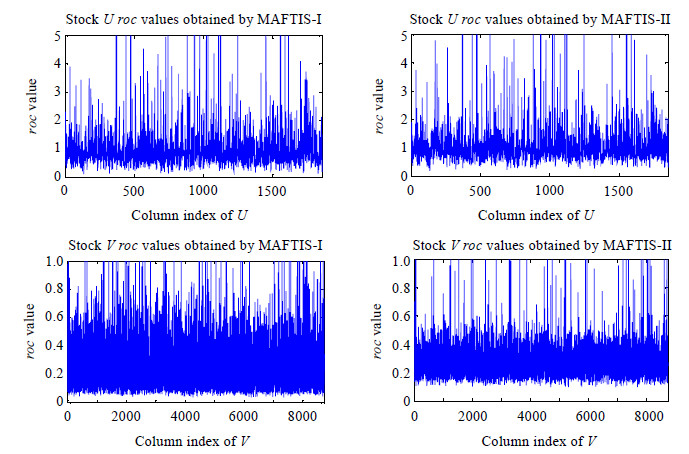
对于在每一个数据集上的拟合结果,我们分别计算了其U,V矩阵内部相邻列间后者相对于前者的变化率(即:roc(Ui,Ui+1)和roc(Vj,Vj+1)).其中,对stock的计算结果如图 5所示(其中,第1行对应U,第2行对应V;左图由MAFTIS-1获得,右图由MAFTIS-II获得),对traffic数据集的计算结果则如图 6所示(其中:第1行对应U,第2行对应V;左图由MAFTIS-1获得,右图由MAFTIS-II获得).
|
Fig.5 he roc values of the stock data 图 5 在stock数据上获得的roc值 |
|
Fig.6 The roc values of the traffic data 图 6 在traffic数据上获得的roc值 |
综合图 5、图 6的结果,矩阵U所对应的roc值在两个数据集的所有结果上的变化都没有明显的趋势;特别地,在相同的数据集上,由不同模型获得的roc值的分布也没有显著差别.这一现象支持了我们对U的解释,即:其所有的组成向量是独立同分布的,彼此的取值没有直接的影响.对于矩阵V,我们发现:在stock数据集上, MAFTIS-I对应的roc曲线比由MAFTIS-II得到的曲线更为光滑,显示在MAFTIS-I的解释下,影响股价的外部环境的变化趋势比由MAFTIS-II描述的结果更为稳定,因而MAFTIS-I的结果具有更好的可解释性.但我们同时注意到:MAFTIS-I对应的曲线整体在y=0.2附近,MAFTIS-II的曲线则围绕y=0.1作锯齿状的上下波动.而前文对stock数据的分析显示,其|roi|值主要聚集在以y=0.1为中心的区域,这与MAFTIS-II曲线的取值区间相吻合.这一现象也解释了在表 2的结果中,MAFTIS-II的表现优于MAFTIS-I的原因.
对于traffic数据集,由图 6第2行的两图可以看到:由MAFTIS-I和MAFTIS-II得到的V矩阵的roc值变化都非常剧烈,然而MAFTIS-I对应的roc值主要分布在区间[0.1,0.6]中,MAFTIS-II对应的roc值则主要落在区间[0.2,0.4]内.对比图 2中traffic数据的roi值分布,由MAFTIS-I获得的结果与其更为接近.
此外,由于图 6中的数据过于密集,为更好地了解其V矩阵的roc值变化的特点,我们在图 7中以0.2为最大上界,分别统计了对于分别由MAFTIS-I和MAFTIS-II获得的V矩阵roc值的累积密度分布.在图 7中,‘*’对应MAFTIS-I,‘+’对应MAFTIS-II.可以看出:对于MAFTIS-I获得的结果,有超过50%的roc值在0.2以下;而对于MAFTIS-II,这一比例仅不到30%.两者比较,前者反映的变化趋势更为稳定.也支持了我们基于stock数据集的roc值分析所作的论断,即,MAFTIS-I的拟合结果具有更好的可解释性.

|
Fig.7 The cdf of the roc values of the V factor matrix obtained from the traffic data 图 7 Traffic数据的V因子矩阵的roc值分布统计 |
● 收敛速度
同样使用前文Given 50%的设置,分别记录了MAFTIS-I,MAFTIS-II在stock和traffic两个数据集上前300次循环中计算获得的RMSE,具体如图 8所示.

|
Fig.8 The convergence speed of MAFTIS on the stock and traffic data 图 8 MAFTIS的收敛速度分析 |
图 8第1行对应了在stock数据上的结果,第2行对应了在traffic数据上的结果;左侧子图对应MAFTIS-I,右侧子图对应MAFTIS-II.所有子图的横坐标记录循环的次数,纵坐标代表RMSE的取值.
从图 8可以看出,MAFTIS-I和MAFTIS-II的收敛速度较为一致.在stock数据集上,它们的RMSE在前100次循环的下降比较明显,其后几乎保持平稳;在traffic数据集上,在前50个循环后,其RMSE即基本保持稳定.这也显示了MAFTIS在实际应用中的有效性.
5 总结与工作展望时序数据是日常生活中最为常见的数据类型之一,在本文的工作中,我们提出了一种适用于时序数据的矩阵分解模型MAFTIS:我们首先提出了一个适合于描述时序数据的概率图模型,在该模型中,我们提出使用两种不同的分布来描述时序数据中相邻时间点上的数据间的联系;根据这一描述,进而我们相应地导出了两种不同的矩阵分解模型MAFTIS-I和MAFTIS-II.
我们分别给出了对MAFTIS-I,MAFTIS-II的求解策略,并在两个不同性质的时序数据集上检验了本文模型在数据恢复应用中的性能表现.我们的实验结果显示:当数据在时间轴上是以渐变的方式发生变化时, MAFTIS-II可能会获得最好的预测结果;而当数据的变化是以突变的形式发生时,MAFTIS-I可能更为合适.
容易看出,本文算法成功的关键在于结构化先验的引入.然而在另一方面,出于实际计算效率的考虑,本文只讨论了确定的链式先验的情况.
显然,本文工作的一个重要推广方向是对不确定的复杂先验的矩阵分解的研究.为此,我们至少还需解决如下两个子问题:
(1) 如何根据不完整的数据获得数据之间的结构关系?
(2) 如何把复杂的结构先验融入到矩阵的分解过程之中?
其中,对于问题(1),文献[30, 31]等工作已经作了有益的探索,这将对问题(2)的研究起到一定的促进作用.然而,考虑到复杂先验对计算效率的影响,对适用于大规模数据的高效矩阵分解算法的研究仍将是我们未来关注的焦点之一.
| [1] | Bell R, Koren Y, Volinsky C. Matrix factorization techniques for recommender systems. IEEE Computer, 2009.42-49 . |
| [2] | Koren K. Factorization meets the neighborhood: A multifaceted collaborative filtering model. In: Proc. of the 14th ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. ACM Press, 2008.426-434 . |
| [3] | Salakhutdinov R, Mnih A. Probabilistic matrix factorization. In: Proc. of the NIPS. 2007. |
| [4] | Xu MJ, Zhu J, Zhang B. Bayesian nonparametric maximum margin matrix factorization for collaborative prediction.In: Proc. of the Advances in Neural Information Processing Systems (NIPS 2012). 2012. |
| [5] | Srebro N, Rennie JDM, Jaakkola T. Maximum margin matrix factorization. In: Proc. of the Advances in Neural Information Processing Systems 17. |
| [6] | Balakrishnan S, Chopra S. Collaborative ranking. In: Proc. of the 5th Int’l Conf. on Web Search and Data Mining.2012 . |
| [7] | Weimer M, Karatzoglou A, Le QV, Smola A. CofiRank—Maximum margin matrix factorization for collaborative ranking. In: Proc. of the NIPS. 2007. |
| [8] | Krohn-Grimberghe A, Drumond L, Freudenthaler C. Multi-Relational matrix factorization using bayesian personalized ranking for social network data. In: Proc. of the 5th ACM Int’l Conf. on Web Search and Data Mining. 2012.173-182 . |
| [9] | Vapnik VN. Statistical Learning Theory. Wiley-Interscience, 1998. |
| [10] | Fazel M, Hindi H, Boyd S. A rank minimization heuristic with application to minimum order system approximation. In: Proc. of the American Control Conf.Arlington, 2001 . |
| [11] | Recht B, Fazel M, Parrilo P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Review, 2008,52(3):471-501 . |
| [12] | Candès EJ, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathermatics, 2008,9: 717-772 . |
| [13] | Candès EJ, Tao T. The power of convex relaxation: Near-Optimal matrix completion. IEEE Trans. on Information Theory, 2009,56(5): 2053-2080 . |
| [14] | Srebro N, Schraibman A. Rank, trace-norm and maxnorm. In: Proc. of the 18th Annual Conf. on Learning Theory.2005 . |
| [15] | Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. MIT Press, 2009. |
| [16] | Salakhutdinov R, Mnih A. Bayesian probabilistic matrix factorization using MCMC. In: Proc. of the ICML. 2008. |
| [17] | Adams R, Dahl G, Murray I. Incorporating side information in probabilistic matrix factorization with gaussian processes. In: Proc. of the UAI. 2010. |
| [18] | Porteous I, Asuncion A, Welling M. Bayesian matrix factorization with side information and dirichlet process mixtures. In: Proc. of the AAAI. 2010. |
| [19] | Stephen B, Vandenberghe L. Convex Optimization. Cambridge University Press, 2009. |
| [20] | Candes EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. on Information Theory, 2006,52(2):489-509 . |
| [21] | Bertsekas DP. Nonlinear Programming. 2nd ed., Athena Scientific, 1999. |
| [22] | Tibshirani R, Saunders M. Sparsity and smoothness via the fused lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2005,67(1):91-108 . |
| [23] | Jerome F, Hastie T, Hofling H, Tibshirani R. Pathwise coordinate optimization. The Annals of Applied Statistics, 2007,1(2): 302-332 . |
| [24] | Golub, GH, Van Loan CF. Matrix Computations. Vol.3, JHU Press, 2012. |
| [25] | Marlin B. Collaborative filtering: A machine learning perspective [MS. Thesis]. University of Toronto, Computer Science Department, 2004. |
| [26] | Tipping ME, Bishop CM. Probabilistic principal component analysis. Journal of the Royal Statistical Society (Series B), 1999,61(3): 611-622 . |
| [27] | Qu L, Hu JM, Li L, Zhang Y. PPCA-Based missing data imputation for traffic flow volume: A systematical approach. IEEE Trans. on Intelligent Transportation Systems, 2009 . |
| [28] | http://lear.inrialpes.fr/people/verbeek/software.php |
| [29] | http://www.utstat.toronto.edu/rsalakhu/BPMF.html |
| [30] | Kolar M, Xing E. Consistent covariance selection from data with missing values. In: Proc. of the ICML. 2012. |
| [31] | Stadler N, Buhlmann P. Missing values: Sparse inverse covariance estimation and an extension to sparse regression. Statistics and Computing, 2009 . |
 2015, Vol. 26
2015, Vol. 26


