Independence-Friendly (IF)逻辑是一阶逻辑的保守扩张,它是由Hintikka和Sandu在文献[1]中首次提出的.其主要特点是能够表达量词间的相互依赖和独立关系,例如其中的公式:
| $\forall x\forall y(\exists z/\forall y)(\exists t/\forall x)p\left( {x,y,z,t} \right)$ | (1) |
在语义上表示对任意的x和y,存在依赖于x但不依赖于y的z,以及依赖于y但不依赖于x的t,使得p(x,y,z,t)是真的.在一阶逻辑中,如果一个存在量词$\exists $z在全称量词$\forall $y的辖域中,那么变量z的取值一定依赖于变量y的取值.但在IF逻辑中,若存在量词$\exists $z虽然在全称量词$\forall $y的辖域中但其后标有/$\forall $y,则z的取值不依赖于y的取值.换句话说,IF逻辑通过对量词后面标注/ (称为Slash)来表达量词间的相互依赖和独立关系.这使得IF逻辑比一阶逻辑具有更强的表达能力.例如,上面的公式(1)在一阶逻辑中就无法通过对量词的线性重组而得到表达.
由于IF逻辑较强的表达能力和它采用的关于不完全信息的博弈语义,IF逻辑自提出以来已经受到许多学者的关注和研究[1-8].特别是文献[5]将IF逻辑进一步扩张,得到所谓的Extended IF逻辑.Extended IF逻辑包含有两种否定:一种是IF逻辑中也有的强否定$ \sim $;另一种是IF逻辑中没有的弱否定$\neg $.强否定$ \sim $和通常所见否定算子的逻辑功能类似:公式$ \sim A$是将公式A中的所有算子和原子变为它们的对偶而得到的.但弱否定$\neg $不能运用于公式的任何位置:它只能运用于整个IF逻辑公式的前面.例如,$\forall x\forall y\neg \forall z(\exists t/\forall x)p\left( {x,y,z,t} \right)$在Extended IF逻辑中是非法的表达.这种有点奇怪的情形主要是因为现有的IF逻辑方法已经不能为$\neg $提供合理的语义.因此,这就需要有更好更广的方法出现.
2006年,Japaridze为公理化可计算性逻辑理论[9, 10],提出了一种新的证明理论和方法——Cirquent演算[11].相比于传统的证明理论,该方法研究处理的是一种基于图的电路式结构——Cirquent,而不是传统的公式、相继式等树形结构.这种结构的最大特点是允许分享子结构.例如在图 1表示的Cirquent中(这是文献[12]给出的Cirquent的概念,本文所讨论的Cirquent概念将比这个更广),同一个孩子可被不同的父亲分享(即不同的父亲可以有相同的孩子),而这是传统的树形结构所不允许的.

|
Fig.1 图 1 |
正是由于这个特点,Cirquent演算具有很强的表达能力和很高的证明效率.文献[12]证明了即使限制在命题逻辑水平,相应的Cirquent演算系统CL8也比传统相继式演算系统的证明效率有指数级的提高.这就使得Cirquent演算在知识库系统、人工智能行为规划、电路等价性验证等领域有着良好的应用前景和广阔的发展空间.该理论自提出以来,已经在基础理论方面得到了进一步的研究和发展[12, 13, 14, 15, 16, 17, 18, 19].
回到前面提到的Extended IF逻辑.除了其弱否定$\neg $的逻辑行为有点奇怪之外,Extended IF逻辑自提出以来的另一个遗憾就是:其命题部分至今没有得到公理化.Japaridze在文献[13]中对Cirquent概念进行了一系列的推广,特别是将Cirquent概念推广到带有簇和级两个参数(正规定义见后文)的水平.形象地说,簇是推广了的逻辑与门或或门.每个簇可看作是同类型的若干个门组成的集合,在同一个簇里的这些门,同时(平行地)分享共同的选择(都选择左或者都选择右).级可看作是比簇更高一级的操控台,每个级是若干个簇组成的集合.所有级的线性排列指明了这些操控台应该按怎样的顺序执行选择.文献[13]指出:带有簇和级的Cirquent能够表达命题联结词间的相互依赖和独立关系,而这正是Extended IF逻辑为发展其命题部分所寻求的.因此,人们可利用Cirquent演算将Extended IF逻辑进行公理化和扩张.这里仅举一个简单的例子说明两者的上述关系,例如Extended IF逻辑中的公式:
| $\forall x(\exists y/\forall x)p\left( {x,y} \right)$ | (2) |
假设论域是{1,2},则公式(2)可改写为
| $(p\left( {1,1} \right){ \vee ^y}/{ \wedge ^x}p\left( {1,2} \right)){ \wedge ^x}(p\left( {2,1} \right){ \vee ^y}/{ \wedge ^x}p\left( {2,2} \right))$ | (3) |
进一步地,将上面的p(1,1),p(1,2),p(2,1),p(2,2)改写为原子p,q,r,s,则公式(3)变为如下的命题公式:
| $(p{ \vee ^y}/{ \wedge ^x}q){ \wedge ^x}(r{ \vee ^y}/{ \wedge ^x}s)$ | (4) |
这里,我们将$\forall $x改为$ \wedge $x,$\exists $y改为$ \vee $y,其中的上标x,y表明相应的命题联结词$ \vee $或$ \wedge $是由哪个量词得到的;同时,用$ \vee $y/$ \wedge $x表明标有上标y的命题联结词$ \vee $不依赖于(独立于)标有上标x的命题联结词$ \wedge $.最后,根据文献[13]的Descriptions 7.4,公式(4)变为如下的Cirquent:
| $(p{ \vee _{{1^1}}}q){ \wedge _{{2^2}}}(r{ \vee _{{1^1}}}s)$ | (5) |
在Cirquent中,若一个联结词的下标为ki,则表明该联结词属于簇k,且簇k属于i级.从而,公式(5)中同属于簇1的两个联结词$ \vee $独立于属于簇2的联结词$ \wedge $.从这个例子我们确实看到,带有簇和级的Cirquent能够表达命题联结词间的相互依赖和独立关系.同时,带有簇和级的Cirquent对Extended IF逻辑的弱否定$\neg $的问题也迎刃而解(见文献[13]的Descriptions 7.5,Descriptions 7.6).但是,文献[13]的上述结论只是从语义角度给出的,并没有给出具体的公理系统.
基于上述背景,本文从语构角度出发,给出了关于Cirquent语义(命题水平)可靠完备的形式系统EIFP.该系统是带有簇和级两个参数的Cirquent演算系统,它能很好地解释、表达命题联结词间的相互依赖和独立关系,从而为Extended IF逻辑的命题部分提供了一个可靠完备的公理系统,使Extended IF逻辑在命题水平得到了真正意义上的公理化.我们将看到:本文给出的系统是经典命题逻辑系统的扩张,同时也是文献[19]中系统IFP的进一步扩张.
第1节介绍与本文相关的基本概念[13].第2节给出Cirquent演算系统EIFP的公理和推理规则,证明所有推理规则是双向保真的,最后证明系统EIFP的可靠性与完备性.
1 预备知识我们用大写字母P,Q,R,S,…表示原子,原子P及其否定$\neg $P称为文字.本文所讨论的公式是(由文字和二元联结词$ \wedge $,$ \vee $生成的,且$\neg $只运用于原子的)经典命题逻辑公式.
Cirquent是带有簇和级两个参数的公式(在Cirquent演算理论中,Cirquent有更广的定义(见文献[13])).其中,
● 簇是对公式中出现的所有$ \wedge $,$ \vee $联结词组成的集合的划分(划分成的子集也称为簇),且满足条件:同一簇中的联结词具有相同的类型($ \wedge $或$ \vee $);
● 级是对所有簇组成的集合的进一步划分,该划分将所有簇组成的集合划分成两个子集(这两个子集也称为级),且满足条件:同一级中的簇具有相同的类型.
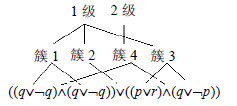
每个簇有唯一的正整数与其对应,称为簇ID.簇k是指簇的ID是k.包含$ \wedge $-簇的级称为合取级,包含$ \vee $-簇的级称为析取级.若簇k在第1级(第2级)中,我们说簇k在1级(簇k在2级).例如,图 2表示一个带有4个簇2个级(1级为析取级,2级为合取级)的Cirquent.
|
Fig.2 图 2 |
为了节省空间和表达方式的紧致,本文将用公式的形式表达Cirquent,只是在公式中出现的每个联结词右下角加注下标ki——表明该联结词属于簇k且簇k在i级(i$ \in ${1,2}).例如,上段示例中的Cirquent将表示为
$((q{ \vee _{{1^1}}}\neg q){ \wedge _{{4^2}}}(q{ \vee _{{1^1}}}\neg q)){ \vee _{{2^1}}}((p{ \vee _{{3^1}}}r){ \wedge _{{4^2}}}(q{ \vee _{{3^1}}}\neg p)).$
在一个给定的Cirquent C中,若簇k的成员只有一个,则称簇k是单身的;否则,簇k是非单身的.若C中所有的簇都是单身的,则称C是经典的;否则,称C是非经典的.C中一个联结词a的水平,记为LC(a),是所有使得a在其辖域中的联结词b的个数.若联结词b在联结词a的辖域中且LC(b)=LC(a)+1,则称b为a的孩子,a为b的父亲.关系后代和祖先分别是关系孩子和父亲的传递闭包.联结词a和它的一个后代b之间的距离是一个正整数k,使得k=LC(b)-LC(a);当a和b之间的距离小于a和其另一个后代c之间的距离,我们称b与a比c与a近.进一步,对任意的两个联结词a和b,将它们最近的共同祖先记为$\underline {ab} $.最后,若C包含后代和祖先在
同一个簇中的情形,则称C是遗传的;否则,称C是非遗传的.
一个解释是一个函数*:{P,Q,R,S,…}$ \to ${ ,⊥},并且通过($\neg $P)*=
,⊥},并且通过($\neg $P)*= 当且仅当P*=⊥扩展到所有文字.
当且仅当P*=⊥扩展到所有文字.
设i$ \in ${1,2}.一个i-选择是一个函数fi:{1,2,3,…}$ \to ${左,右}.进一步地,一个选择是二元组$\vec f$=(f1,f2),其中对任意i$ \in ${1,2},fi是i-选择.设C是Cirquent,且C有子Cirquent $A{ \vee _{{k^i}}}B$(或$A{ \wedge _{{k^i}}}B$).若fi(k)=左,称$A{ \vee _{{k^i}}}B$(或$A{ \wedge _{{k^i}}}B$)的被选项是A;若fi(k)=右,称$A{ \vee _{{k^i}}}B$(或$A{ \wedge _{{k^i}}}B$)的被选项是B.
设C是Cirquent,*是一个解释,$\vec f$是一个选择.以下给出“关于(*,$\vec f$)是真的”的定义:
● C的文字L关于(*,$\vec f$)是真的当且仅当L*= ;
;
● C的子Cirquent $A{ \vee _{{k^i}}}B$(或$A{ \wedge _{{k^i}}}B$)关于(*,$\vec f$)是真的当且仅当其被选项关于(*,$\vec f$)是真的.
进一步地,C在解释*下是真的当且仅当${a_1}{f_1}{a_2}{f_2}$使得C关于(*,(f1,f2))是真的.其中,aifi表示:对任意i-选择fi (若C的i级是合取级)以及存在一个i-选择fi (若C的i级是析取级).最后,我们称C是有效的当且仅当它在任意解释下都是真的.
以下为叙述方便,当需要指明Cirquent C的1级和2级的类型时,我们将用$C_{1 \vee }^{2 \wedge }$表示其1级是析取级,2级是合取级;用$C_{1 \wedge }^{2 \vee }$表示其1级是合取级,2级是析取级.
由上述语义定义容易看到:经典命题逻辑中的公式等同于本文经典的Cirquent $C_{1 \vee }^{2 \wedge }$,只是将$C_{1 \vee }^{2 \wedge }$中所有联结词右下角的下标(ki)省略而已.对经典的Cirquent $C_{1 \vee }^{2 \wedge }$(即,经典命题逻辑公式),$C_{1 \vee }^{2 \wedge }$是有效的当且仅当它关于
经典命题逻辑语义是有效的.而且,经典逻辑语义中一个公式在某个解释*下是真的当且仅当本文语义中存在一个1-选择f1对任意的2-选择f2,使得该公式关于(*,(f1,f2))是真的.因此,本文所介绍的逻辑是经典命题逻辑的
保守扩张,经典命题逻辑只是本文限制在经典的$C_{1 \vee }^{2 \wedge }$水平的逻辑部分.另外,本文的逻辑也是文献[19]中只带有$ \vee $-簇(一个参数)的逻辑保守扩张,文献[19]的逻辑是本文限制在$C_{1 \vee }^{2 \wedge }$水平且$ \wedge $-簇均是单身的逻辑部分.
2 主要结论 2.1 系统EIFP本节给出系统EIFP的公理和推理规则.在给出公理和推理规则之前,我们先给出一个定义和两个引理.
对于仅包含非单身$ \wedge $-簇(即,$ \vee $-簇均是单身)的非遗传Cirquent $C_{1 \vee }^{2 \wedge }$,反复执行以下步骤,直到$C_{1 \vee }^{2 \wedge }$变为经典的:任选$C_{1 \vee }^{2 \wedge }$中属于非单身$ \wedge $-簇的一个联结词a,将其下标k2变为l2,其中,l2是在$C_{1 \vee }^{2 \wedge }$(包括下标)中没有出现过的任意正整数.我们称上述过程为$C_{1 \vee }^{2 \wedge }$的经典化,并将经典化的结果记为 ($(C_{1 \vee }^{2 \wedge })$).对于仅包含非单身$ \vee $-簇(即,$ \wedge $-簇均是单身)的非遗传Cirquent $C_{1 \wedge }^{2 \vee }$,其经典化定义类似,只是将上述过程中的$ \wedge $-改为$ \vee $-,$ \vee $-改为$ \wedge $-.
($(C_{1 \vee }^{2 \wedge })$).对于仅包含非单身$ \vee $-簇(即,$ \wedge $-簇均是单身)的非遗传Cirquent $C_{1 \wedge }^{2 \vee }$,其经典化定义类似,只是将上述过程中的$ \wedge $-改为$ \vee $-,$ \vee $-改为$ \wedge $-.
容易验证以下两个引理成立:
引理1. 设*是任意的解释:
(i) 一个经典的Cirquent $C_{1 \vee }^{2 \wedge }$在*下是真的当且仅当将$C_{1 \vee }^{2 \wedge }$中的级互换而得到的Cirquent在*下是真的;
(ii) 一个经典的Cirquent $C_{1 \wedge }^{2 \vee }$在*下是真的当且仅当将$C_{1 \wedge }^{2 \vee }$中的级互换而得到的Cirquent在*下是真的.
引理2. 设*是任意的解释:
(i) 一个仅包含非单身$ \wedge $-簇的非遗传Cirquent $C_{1 \vee }^{2 \wedge }$在*下是真的当且仅当 ($(C_{1 \vee }^{2 \wedge })$)在*下是真的;
($(C_{1 \vee }^{2 \wedge })$)在*下是真的;
(ii) 一个仅包含非单身$ \vee $-簇的非遗传Cirquent $C_{1 \wedge }^{2 \vee }$在*下是真的当且仅当 ($C_{1 \wedge }^{2 \vee }$)在*下是真的.
($C_{1 \wedge }^{2 \vee }$)在*下是真的.
由引理1容易得到:对经典的Cirquent,我们没必要区分是$C_{1 \vee }^{2 \wedge }$还是$C_{1 \wedge }^{2 \vee }$(即,与级无关).为了表达和叙述方
便,本文以下部分在表达Cirquent时将总是省去单身簇的ID及其所属的级(即,省去属于单身簇的联结词的下标ki).这样,经典的Cirquent就自动变成了经典命题逻辑公式.
我们将看到,系统EIFP的推理规则可作用于Cirquent的任意深度而不仅仅是在根部进行.因此,系统EIFP采取的是深度推理[20].正因为此,在表达推理规则时也借用了深度推理的表达:将用$\Phi ${}或$\psi ${}来表示任意的在子结构中带有一个空{}的Cirquent.空{}可被任意的Cirquent代替.例如,若$\Phi \{ \} = (q{ \vee _{{1^2}}}p){ \vee _{{1^2}}}(\{ \} \wedge q)$,则$\Phi \{ \neg p\} = (q{ \vee _{{1^2}}}p){ \vee _{{1^2}}}(\neg p \wedge q),\Phi \{ q\} = (q{ \vee _{{1^2}}}p){ \vee _{{1^2}}}(q \wedge q)$以及$\Phi \{ p{ \vee _{{1^2}}}q\} = (q{ \vee _{{1^2}}}p){ \vee _{{1^2}}}((p{ \vee _{{1^2}}}q) \wedge q)$.
系统EIFP的公理包括(引理1和引理2解释了系统EIFP的公理包括如下3部分的合理性):
(i) 经典命题逻辑中的所有重言式;
(ii) 所有仅包含非单身$ \wedge $-簇的非遗传Cirquent $C_{1 \vee }^{2 \wedge }$,其中,$C_{1 \vee }^{2 \wedge }$使得 ($(C_{1 \vee }^{2 \wedge })$)是重言式;
($(C_{1 \vee }^{2 \wedge })$)是重言式;
(iii) 所有仅包含非单身$ \vee $-簇的非遗传Cirquent $C_{1 \wedge }^{2 \vee }$,其中,$C_{1 \wedge }^{2 \vee }$使得 ($C_{1 \wedge }^{2 \vee }$)是重言式.
($C_{1 \wedge }^{2 \vee }$)是重言式.
系统EIFP的推理规则如图 3所示,包括规则I、规则II、规则III.其中,A,B,C,D代表任意的Cirquent,k是某个正整数(代表某个簇的ID),$ \odot \in \{ \wedge , \vee \} ,o \in \{ \wedge , \vee ,{ \wedge _l},{ \vee _l}\} $(l是任意正整数使得簇l是非单身的).特别注意:在同一规则中,e的所有出现均代表同一符号(如均是$ \vee $),o的所有出现也均代表同一符号(如均是$ \vee $l).

|
Fig.3 Inference rules of system EIFP 图 3 系统EIFP的推理规则 |
说明:
(i) 规则I和规则II均有左、右两个版本,适用于任意Cirquent;规则III有$C_{1 \vee }^{2 \wedge },C_{1 \wedge }^{2 \vee }$两个版本,其中,规则III($C_{1 \vee }^{2 \wedge }$)只适用于1级是析取级、2级是合取级的Cirquent,规则III($C_{1 \wedge }^{2 \vee }$)只适用于1级是合取级、2级是析取级的Cirquent;
(ii) 如图 3所示,在每条规则的运用中,将前提(结论)中标有下标k的联结词称为这次运用在前提(结论)中的关键联结词;
(iii) 图 3中,我们仅用下标k(或l)来表示相应联结词所属的簇(而没用ki(或li)来表明其所属的簇和簇所属的级),这是因为这样表示既简单又不会引起表达的混淆.例如:若规则运用于Cirquent $C_{1 \vee }^{2 \wedge }$,则所有$ \vee $-联结词均是1级,所有$ \wedge $-联结词均是2级;若规则运用于Cirquent $C_{1 \wedge }^{2 \vee }$,则所有$ \wedge $-联结词均是1级,所有$ \vee $-联结词均是2级.
Cirquent C在系统EIFP中的一个证明是由Cirquent组成的序列C0,C1,…,Cn,使得C0是EIFP中的公理, Cn=C,且Ci是由Ci-1运用EIFP中的推理规则得到的(0≤i≤n).C在系统EIFP中是可证的当且仅当C在EIFP中存在一个证明.
引理3. 设$\Phi \{ A{ \odot _{{k^i}}}B\} $是Cirquent(其中,$ \odot \in \{ \wedge , \vee \} ,i \in \left\{ {1,2} \right\},k$是正整数),$\vec f$是一个选择,*是一个解释.$\Phi \{ A{ \odot _{{k^i}}}B\} $关于(*,$\vec f$)是真的当且仅当fi(k)=左时$\Phi ${A}关于(*,$\vec f$)是真的,fi(k)=右时$\Phi ${B}关于(*,$\vec f$)是真的.
证明:对$\Phi ${}中联结词的个数作归纳证明.若$\Phi ${}中联结词的个数为0,则$\Phi \{ A{ \odot _{{k^i}}}B\} = A{ \odot _{{k^i}}}B$,$\Phi ${A}=A, $\Phi ${B}=B.由关于(*,$\vec f$)真的定义,$A{ \odot _{{k^i}}}B$关于(*,$\vec f$)是真的当且仅当fi(k)=左时其被选项A关于(*,$\vec f$)是真的, fi(k)=右时其被选项B关于(*,$\vec f$)是真的.
假设$\Phi ${}中联结词的个数为n时命题成立,证明$\Phi ${}中联结词的个数为n+1时命题也成立,分$\Phi ${}的主要联结词是$ \wedge $,$ \vee $,$ \wedge $m,$ \vee $m(m是任意正整数使得簇m是非单身的)这4种情况讨论.这里只讨论$\Phi ${}的主要联结词是$ \vee $ 的情形,其他情形类似可证.不妨设$\Phi \{ A{ \odot _{{k^i}}}B\} = \Psi \{ A{ \vee _{{k^i}}}B\} \vee C$,其中,$\Phi ${}的主要联结词$ \vee $在某个单身簇l中($\Phi \{ A{ \odot _{{k^i}}}B\} = \Psi \{ A{ \wedge _{{k^i}}}B\} \vee C$的情形类似可证).进一步分以下两种情形讨论:
(1) fi(l)=右,则$\Psi \{ A{ \vee _{{k^i}}}B\} \vee C$关于(*,$\vec f$)是真的当且仅当被选项C关于(*,$\vec f$)是真的.同理,$\psi ${A}$ \vee $C(或$\psi ${B}$ \vee $C)关于(*,$\vec f$)是真的当且仅当被选项C关于(*,$\vec f$)是真的.而$\Phi ${A}即$\psi ${A}$ \vee $C,$\Phi ${B}即 $\psi ${B}$ \vee $C,从而结论显然成立;
(2) fi(l)=左,则$\Psi \{ A{ \vee _{{k^i}}}B\} \vee C$关于(*,$\vec f$)是真的当且仅当被选项$\Psi \{ A{ \vee _{{k^i}}}B\} $关于(*,$\vec f$)是真的.由归纳假设,$\Psi \{ A{ \vee _{{k^i}}}B\} $关于(*,$\vec f$)是真的当且仅当fi(k)=左时$\psi ${A}关于(*,$\vec f$)是真的,fi(k)=右时$\psi ${B}关于(*,$\vec f$)是真的.而fi(k)=左时$\psi ${A}关于(*,$\vec f$)是真的,fi(k)=右时$\psi ${A}关于(*,$\vec f$)是真的当且仅当fi(k)=左时$\Phi ${A}关于(*,$\vec f$)是真的,fi(k)=右时$\Phi ${B}关于(*,$\vec f$)是真的. □
定理1. 系统EIFP中的所有规则都是双向保真的.
证明:我们仅证明规则III($C_{1 \wedge }^{2 \vee }$)双向保真,其他规则类似可证.设*是任意的解释,以下证明前提$\Phi ${(AoC)$ \wedge $k(BoD)}在*下是真的当且仅当结论$\Phi \{ (A{ \wedge _k}B)o(C{ \wedge _k}D)\} $在*下是真的.分3种情况讨论如下.
(1) o是$ \vee $l或$ \wedge $l.
由真的定义,前提$\Phi ${(AoC)$ \wedge $k(BoD)}在*下是真的当且仅当对任意的1-选择f1存在一个2-选择f2,使得前提关于(*,(f1,f2))是真的(显然,(f1,f2)也是结论的一个选择).由引理3,前提关于(*,(f1,f2))是真的当且仅当f1(k)=左时
$\Phi ${AoC}关于(*,(f1,f2))是真的,或f1(k)=右时$\Phi ${BoD}关于(*,(f1,f2))是真的.另一方面,连用两次引理3,我们有结论:关于(*,(f1,f2))是真的当且仅当f1(k)=左时$\Phi ${AoC}关于(*,(f1,f2))是真的,或f1(k)=右时$\Phi ${BoD}关于(*,(f1,f2))是真
的.所以,前提关于(*,(f1,f2))是真的当且仅当结论关于(*,(f1,f2))是真的.而对任意的1-选择f1,存在一个2-选择f2,使得结论关于(*,(f1,f2))是真的当且仅当结论在*下是真的.
(2) o是$ \wedge $.
设前提是$\Phi ${(A$ \wedge $mC)$ \vee $k{B$ \wedge $nD}},结论是$\Phi ${(A$ \wedge $kB)$ \wedge $h{C$ \wedge $kD}},其中,簇m,n,h均是单身的.设结论在*下是真的.设g1是结论的任意1-选择,则g1分别在簇k,h上的附值一定是以下4种情况之一:左、左;左、右;右、左;右、右.若g1(k)=左、g1(h)=左,则由真的定义及引理3,存在结论的2-选择g2,使得$\Phi ${A}关于(*,(g1,g2))是真的;同理,若g1(k)=左、g1(h)=右,存在结论的2-选择u2,使得$\Phi ${C}关于(*,(g1,u2))是真的;若g1(k)=右、g1(h)=左,存在结论的2-选择v2,使得$\Phi ${B}关于(*,(g1,v2))是真的;若g1(k)=右、g1(h)=右,存在结论的2-选择w2,使得$\Phi ${D}关于(*,(g1,w2))是真的.显然,g2,u2,v2,w2也均是前提的2-选择.设f1是前提任意的1-选择,则同上,f1在簇k,m,n上的附值共有23=8种情况.由g1,f1的任意性可知,g1,f1分别限制在$\Phi ${A},$\Phi ${B},$\Phi ${C},$\Phi ${D}上时是相同的.所以当f1(k)=左、f1(m)=左时,取前提的2-选择g2,则$\Phi ${A}关于(*,(f1,g2))是真的;同理,当f1(k)=左、f1(m)=右时,取前提的2-选择u2,则$\Phi ${C}关于(f1,u2)是真的;当f1(k)=右、f1(n)=左时,取前提的2-选择v2,则$\Phi ${B}关于(*,(f1,v2))是真的;当f1(k)=右、f1(n)=右时,取前提的2-选择w2,则$\Phi ${D}关于(*,(f1,w2))是真的.所以,对前提任意的1-选择f1,总存在前提的2-选择f2,使得前提关于(*,(f1,f2))是真的.故,前提在*下是真的.反之,设前提在*下是真的,同上类似,可证结论在*下是真的.
(3) o是$ \vee $.
设前提是$\Phi ${(A$ \vee $mC)$ \wedge $k{B$ \vee $nD}},结论是$\Phi ${(A$ \wedge $kB)$ \vee $h{C$ \wedge $kD}},其中,簇m,n,h均是单身的.
首先,设结论在*下是真的.设f1是前提任意的1-选择.显然,f1也是结论的1-选择.则由真的定义,对f1存在结论的2-选择f2,使得结论关于(*,(f1,f2))是真的.由引理3(连用两次),当有f1(k)=左时$\Phi ${A$ \vee $hC}关于(*,(f1,f2))是真的,或f1(k)=右时$\Phi ${B$ \vee $hD}关于(*,(f1,f2))是真的.令g2是前提的一个2-选择,满足g2(m)=g2(n)=f2(h),且g2在其他$ \vee $-簇上的定义与f2相同.则当f1(k)=左时$\Phi ${A$ \vee $mC}关于(*,(f1,g2))是真的,或f1(k)=右时$\Phi ${B$ \vee $nD}关于(*,(f1,g2))是真的.再由引理3,我们得到前提关于(*,(f1,g2))是真的.所以前提在*下是真的.
其次,设前提在*下是真的.设f1是结论任意的1-选择.显然,f1也是前提的1-选择.则由真的定义,对f1存在前提的2-选择f2,使得前提关于(*,(f1,f2))是真的.由引理3,当f1(k)=左时$\Phi ${A$ \vee $mC}关于(*,(f1,f2))是真的,或f1(k)=右时$\Phi ${B$ \vee $nD}关于(*,(f1,f2))是真的.令g2是结论的一个2-选择,满足f1(k)=左时g2(h)=f2(m),f1(k)=右时g2(h)=f2(n),且g2在其他$ \vee $-簇上的定义与f2相同.从而有:f1(k)=左时$\Phi ${A$ \vee $hC}关于(*,(f1,g2))是真的,或f1(k)=右时$\Phi ${B$ \vee $hD}关于(*,(f1,g2))是真的.最后再由引理3(连用两次),得到结论关于(*,(f1,g2))是真的.故,结论在*下是真的. □
2.2 系统EIFP的可靠性与完备性本节给出系统EIFP的可靠性与完备性证明.
定理2. Cirquent C是有效的当且仅当它在EIFP中是可证的.
证明:可靠性显然成立.这是因为公理是有效的,再由定理1,所有规则是保真的(从而保有效性),所以由公理和推理规则推出的Cirquent C一定是有效的.现考虑完备性.设Cirquent C是有效的.以下证明C在EIFP中是可证的.分以下几种情况讨论(此证明借鉴(但不同于)文献[19]中相应证明的思路):
(1) 设C是经典的,即,C是经典命题逻辑公式.
则由C的有效性,我们立即得到C是经典命题逻辑中的重言式,从而是EIFP中的公理.
(2) 设C是非经典的Cirquent $C_{1 \vee }^{2 \wedge }$,且$C_{1 \vee }^{2 \wedge }$中只有非单身的$ \wedge $-簇.
自下而上地反复运用规则I,直到当前(最上面)的Cirquent变为非遗传的Cirquent $D_{1 \vee }^{2 \wedge }$.容易看出:每运用一次规则I,当前Cirquent中就减少一对联结词a,b,其中,a,b满足在同一簇中且是后代-祖先的关系.因此,上述过程一定能在有限步内结束.由定理1,规则I是双向保真的,所以$D_{1 \vee }^{2 \wedge }$是有效的.又规则I的运用不会使非单身$ \vee $-簇出现,所以$D_{1 \vee }^{2 \wedge }$是有效的只有非单身$ \wedge $-簇的非遗传Cirquent,从而是EIFP中的公理.
(3) 设C是非经典的Cirquent $C_{1 \wedge }^{2 \vee }$,且$C_{1 \wedge }^{2 \vee }$中只有非单身的$ \vee $-簇.
与情形(2)类似,自下而上地反复运用规则I,直到当前的Cirquent变为非遗传的Cirquent $E_{1 \wedge }^{2 \vee }$.因为规则I是双向保真的,所以$E_{1 \wedge }^{2 \vee }$是有效的.且此过程不会使非单身的$ \wedge $-簇出现,所以$E_{1 \wedge }^{2 \vee }$是有效的只有非单身$ \vee $-簇的非遗传Cirquent,从而是EIFP中的公理.
(4) 设C是非经典的Cirquent $C_{1 \wedge }^{2 \vee }$,且$C_{1 \wedge }^{2 \vee }$中有非单身的$ \wedge $-簇和$ \vee $-簇.
自下而上地建立$C_{1 \wedge }^{2 \vee }$的证明如下:
首先,对当前(最上面的)Cirquent反复运用规则I,直到当前Cirquent变为非遗传的Cirquent $C_{1 \wedge }^{2 \vee }$,则$C_{1 \wedge }^{2 \vee }$是有效的(由定理1).设k1,k2,…,kn(n≥0)是$C_{1 \wedge }^{2 \vee }$中所有非单身的$ \wedge $-簇,任意选取其中一个$ \wedge $-簇ki,反复执行以下3个步骤,直到当前Cirquent中的簇ki变为单身(以下我们用A表示当前的Cirquent):
步骤1. 任意选取满足以下两个条件的一对$ \wedge $-联结词a,b:a,b均在簇ki中;对簇ki中的任意一对$ \wedge $-联结词 c,d,${L^A}(\underline {ab} ) \ge {L^A}(\underline {cd} )$.令m=2,$l = {L^A}(\underline {ab} )$.
步骤2. (a) 反复执行以下两步直到LA(a)=l+1:
(i) 自下而上地对A运用规则II,使得联结词a是这次运用(在结论中)的关键联结词;
(ii) 将这次运用(在前提中)的关键联结词重命名为a;
(b) 反复执行以下两步直到LA(b)=l+1:
(i) 自下而上地对A运用规则II,使得联结词b是这次运用(在结论中)的关键联结词;
(ii) 将这次运用(在前提中)的关键联结词重命名为b;
步骤3. 自下而上地对A运用规则III,使得a,b是这次运用(在结论中)的关键联结词.令m=1.
容易验证,上述3步骤的执行过程保持当前Cirquent的非遗传性.又由文献[19]的定理3.3,该过程可在有限
步内结束(停止).设上述3步骤过程结束时得到的Cirquent是$E_{1 \wedge }^{2 \vee }$,则$E_{1 \wedge }^{2 \vee }$中有n-1个非单身的$ \wedge $-簇(因为此过程不会增加新的非单身簇,且簇ki变成了单身).在$E_{1 \wedge }^{2 \vee }$中任选$ \wedge $-簇kj(j$ \ne $i,1≤j≤n)执行上述类似的过程,则得到Cirquent $F_{1 \wedge }^{2 \vee }$(其中有n-2个非单身$ \wedge $-簇).上述过程每执行一次,当前Cirquent中非单身$ \wedge $-簇的个数减1.因此,最外层的循环过程一定在有限步内结束,且最后得到的Cirquent $G_{1 \wedge }^{2 \vee }$中没有非单身的$ \wedge $-簇.因为上述过程中只用到规则II和规则III,且它们都是双向保真的,所以所有的Cirquent $E_{1 \wedge }^{2 \vee },F_{1 \wedge }^{2 \vee },...,G_{1 \wedge }^{2 \vee }$都是有效的.因为最上面的Cirquent $G_{1 \wedge }^{2 \vee }$是有效的只包含非单身$ \vee $-簇的非遗传Cirquent(已经是EIFP中的公理),所以得到了$C_{1 \wedge }^{2 \vee }$的自下而上的一个证明.
(5) 设C是非经典的Cirquent $C_{1 \vee }^{2 \wedge }$,且$C_{1 \vee }^{2 \wedge }$中有非单身的$ \wedge $-簇和$ \vee $-簇.
与情形(4)类似,可自下而上建立$C_{1 \vee }^{2 \wedge }$的一个证明,只是将情形4过程中的$ \wedge $-均换成$ \vee $-,$ \vee $-均换成$ \wedge $-. □
3 总结与展望本文给出了一个带有簇和2个级的Cirquent演算系统EIFP,证明了该系统关于Cirquent语义(命题水平)的可靠性与完备性.系统EIFP是经典命题逻辑系统的扩张.同时,由于带有簇和级的Cirquent能很好地解释和表达命题联结词间的相互依赖和独立关系,系统EIFP可看作是Extended IF逻辑命题部分的一个可靠完备的公理系统.这使得Extended IF逻辑在命题水平得到了真正意义上的公理化,从而为Extended IF逻辑的发展做出了一定的理论贡献.当然,本文给出的系统还可进一步扩张.由于Cirquent概念有一系列的推广,未来我们还需研究系统EIFP的一系列扩张.其中,首要研究带有簇和任意有限个级(而不是只有2个级)的Cirquent概念,给出相应的推理系统并证明其可靠性与完备性.
| [1] | Hintikka J, Sandu G. Game-Theoretical Semantics. In: van Benthem J, ter Meulen A, eds. Handbook of Logic and Language. North-Holland, 1997. 361-410. |
| [2] | Hodges W. Compositional semantics for a language of imperfect information. Logic Journal of the IGPL, 1997,5(4):539-563 . |
| [3] | Hodges W. Logics of imperfect information: Why sets of assignments? In: van Benthem J, Gabbay DM, Löve B, eds. Proc. of the Interactive Logic. Amsterdam University Press, 2007. 117-133. |
| [4] | Mann AL, Sandu G, Sevenster M. Independence-Friendly Logic: A Game-Theoretic Approach. Cambridge eBook, 2011. |
| [5] | Tulenheimo T. Independence Friendly Logic. Stanford Encyclopedia of Philosophy, 2009. |
| [6] | Väänänen J. Dependence Logic: A New Approach to Independence Friendly Logic. Mathematical Society Student Texts, 2007. |
| [7] | Pietarinen AV. Propositional logic of imperfect information: Foundations and applications. Notre Dame Journal Formal Logic, 2001,42(4):193-210 . |
| [8] | Sandu G, Pietarinen A. Partiality and games: Propositional logic. Logic Journal of the IGPL, 2001,9(1):101-121 . |
| [9] | Japaridze G. Introduction to computability logic. Annals of Pure and Applied Logic, 2003,123:1-99 . |
| [10] | Japaridze G. In the beginning was game semantics. In: Majer O, Pietarinen AV, Tulenheimo T, eds. Proc. of the Games: Unifying Logic, Language and Philosophy. Springer-Verlag, 2009.249-350 . |
| [11] | Japaridze G. Introduction to cirquent calculus and abstract resource semantics. Journal of Logic and Computation, 2006,16(4): 489-532 . |
| [12] | Japaridze G. Cirquent calculus deepened. Journal of Logic and Computation, 2008,18(6):983-1028 . |
| [13] | Japaridze G. From formulas to cirquents in computability logic. Logical Methods in Computer Science, 2011,7(2):1-55 . |
| [14] | Japaridze G. The taming of recurrences in computability logic through cirquent calculus, Part I. Archive for Mathematical Logic, 2013,52:173-212 . |
| [15] | Japaridze G. The taming of recurrences in computability logic through cirquent calculus, Part II. Archive for Mathematical Logic, 2013,52:213-259 . |
| [16] | Xu WY, Liu SY. Soundness and completeness of the cirquent calculus system CL6 for computability logic. Logic Journal of the IGPL, 2012,20:317-330 . |
| [17] | Xu WY, Liu SY. The countable versus uncountable branching recurrences in computability logic. Journal of Applied Logic, 2012,10(4): 431-446 . |
| [18] | Xu WY, Liu SY. The parallel versus branching recurrences in computability logic. Notre Dame Journal of Formal Logic, 2013,54(1): 61-78 . |
| [19] | Xu WY. A propositional system induced by Japaridze’s approach to IF logic. Logic Journal of the IGPL, 2014. |
| [20] | Bruscoli P, Guglielmi A. On the proof complexity of deep inference. ACM Trans. on Computational Logic, 2009,10(2):14 . |
 2015, Vol. 26
2015, Vol. 26


