无线(自主、传感器)网络在军事和民用领域都具有重要的应用前景.无线网络具有节点能量有限、节点资源受限、分布性和多跳通信等特点;这些特点决定了拓扑控制在无线网络研究中的重要性和挑战性.用图论模拟无线网络拓扑结构是很自然的.每个无线节点对应图中的一个顶点,能够直接通信的每对节点由一条边连接,所得图就是无线网络的通信图.拓扑控制的最初目标是从所有可能的边中选择一个连通子集,使边数目减少而所得拓扑上的路由更快、更容易,且能够节约传输能量,从而延长无线网络的寿命.也可以说,拓扑控制的基本任务是选择通信图$G(V,E)$的一个子图$H(V,{E_H}),$使得${E_H} \subseteq E,$在保证网络性能的前提下延长无线网络的寿命.文献[1]首次提到无线网络拓扑控制.
给定n个点的点集V,如何构造连通这些节点的网络?完全通信图是一个选择,使得每两个节点间都有一条边相连,都能直接通信,缺点是边的条数多,为$C(n,2) = \Theta ({n^2}),$且由于干扰的存在,实际无线网络中是不可能实现任意两个节点都能直接通信的.另一方面,n个节点连通所需边最少为n-1条,可构成生成树形状.但是网络设计时,不仅要求连通所有节点,而且要求拓扑尽量满足如下特性[2].
(1) 规模:定义为网络中边的数目.拓扑控制的一个主要目标是使拓扑简单,更易于维护.拓扑的复杂性主要取决于边的数目.所得拓扑边的数目最好与节点的数目呈线性关系,这样的网络我们称为稀疏的网络.一般地,网络连通性和网络稀疏性之间需要加以折中.如果节点丢弃太多链路,网络可能变成分割、不连通,或者节点间路径变长.
(2) 连通性:拓扑控制算法的最基本的要求是,输入图G连通,输出图H也连通.这意味着若G中每对传感器节点{u,v}存在一条从u到v的路径,则在H中也存在一条从u到v的路径.另外,一些拓扑控制算法要求保证k-顶点连通、k-边连通,这意味着移除至少k个顶点、k条边才使图不连通.若k太大,图的规模变大,图变得不再稀疏,因为n个顶点的k-连通图至少需要$kn/2$条边.
(3) 权值:定义为所有边上的权值之和.由于网络必须连通所有节点,则通信图的权值最小为最小生成树的权值.实际网络的权值通常以最小生成树的权值为下界.权值是网络的一个重要衡量指标,通常希望设计的网络权值较小,即为轻量级(lightness)网络.
(4) 度:与一个节点直接通信的节点称为它的邻居节点,邻居节点的个数称为这个节点的度.通信图中节点度的最大值,称为通信图的度.通信图的度有界,意味着规模小;反之不然.若通信图的节点平均度是常数,则图中边的数目是节点的线性倍.
(5) 直径:定义为任意两点之间最短路径的最大值.要提高网络传输的质量和速度,通常要求小直径.
(6) 平面性:通常有效的调度算法要求没有两条边在非顶点处相交.因此,为了使用这些算法,所用拓扑必须是平面的.
(7) 对称性:在许多调度协议中,接收者通过确认信息(ACK)确认数据包的接收.这些ACK信息必须返回给发送者.最简单的方式就是沿原始信息相同的路径反向发送ACK信息.因此,通信链路通常是双向的,即要求拓扑图H是对称的,是无向图.也有的网络环境是单向通信,拓扑图H为有向图.
(8) 容错性和鲁棒性:容错性和鲁棒性与网络的可靠性有关.一旦网络中某些节点或者边不工作,网络会失效.容错性通常定义为使网络失效的节点或者边数目,与拓扑图的k-顶点连通、k-边连通有关.显然,增加k使网络的可靠性更好,即容错性更好,但图有可能变为稠密图,因此最近提出了鲁棒性概念.目前支撑图的容错性和鲁棒性是研究热点.
(9) 干扰:当若干节点同时发送消息时,相互之间会产生干扰.接收节点u处有高干扰,意味着任何想发送信息给u的节点必须使用更高的传输功率,特别是,一些传输可能由于干扰而变得不可行.因此,拓扑控制算法需要降低干扰.无线网络中考虑干扰影响的模型主要有两种:协议干扰模型和物理干扰模型.文献[3]给出了协议干扰模型中显式的干扰定义.
(10) 局部性:在无线网络中,网络拓扑不可能完全可知,因此集中式算法实际是不可行的,需要根据具体的网络条件设计分布式构造算法,或者将一些集中式算法转化为分布式执行.又因为每个节点只能感知到它局部的邻居信息,而不是整个网络的状态信息,此时采用局部的分布式构造算法是最合适的.局部算法的执行过程不仅是分布式的,而且每个节点只需进行常数步的执行就能结束算法.
上述拓扑特性通常不能同时都得到满足,有的特性相互之间是有矛盾的.例如,如果网络要求常数度,小直径要求可能无法满足;边很少或度有限的图没有高容错性.所以无线网络拓扑控制问题通常是上述网络特性需求的权衡,可以看作多目标优化问题.针对大规模、复杂的实际网络,合适的仿真工具进行仿真测试能够很好地帮助设计无线网络[4].
给定通信图$G(V,E)$,拓扑控制时移除一些通信链路后,可能使G中某些节点对间的最短路径变长,网络的直径变大,若所得拓扑图H中所有节点对间的最短路径,与原通信图中相应节点对间最短路径相比,前者不大于后者的t倍,则H称为G的t-支撑图,其中实数t≥1,称为支撑比(stretch factor,spanning ratio).也可以说,图H里的最短路径长度近似等于图G的最短路径长度,参数t代表近似比率.通常t取拓扑图H中任意节点对间的最短路径上的总费用与相应节点对直接通信时费用之比值的最大值,本文与大多数文献一样采用此观点.本文主要探讨支撑图用作无线网络拓扑图的情形,在此前提下,支撑图的基础图G是通信图,两节点之间能够直接传递消息才有边连接.
1986年,Chew在文献[5]中首次研究了支撑图问题.他的主要贡献在于,对给定完全图G的点集进行L1度量的Delaunay三角剖分,得到生成子图H,证明了H中任意两点之间的最短路径至多为这两点之间欧氏距离的$\sqrt {10} $倍,其中两点之间的L1距离定义为两节点x坐标差的绝对值加上y坐标差的绝对值.Chew将研究结果应用于运动规划,试图找到障碍物间最短路径的合理近似.但Chew并没有给出支撑图概念,Peleg和Schäffer在文献[6]中以及Peleg和Ullman在文献[7]中最早明确给出支撑图这一概念.
大量文献提出了在几何图中构造各种性能的t-支撑图的方法[8-10].在几何背景下意味着赋权图$G(V,E)$顶点集是由属于欧氏空间中的点组成,边集是由连接两个点的线段组成,边的长度按照欧氏距离来度量.支撑图H是图G的生成子图,在图H里存在一条x到y的路径,这条路径上所有边的欧氏距离之和不大于$d(x,y)$的t倍,其中$d(x,y)$表示x和y之间的欧氏距离,通常假设G为完全图,所得支撑图通常称为几何支撑图.Levcopoulos和Lingas在文献[11]中首先给出了几何背景下的支撑图概念.此后几何支撑图诸方面都有大量研究.
支撑图有着广泛应用,除了可用于拓扑控制外,还可用于如下几个方面.
(1) 支撑图用于设计旅行售货商等问题的近似算法.旅行售货商问题指的是一个售货商想去几个城市推销商品[12],他希望从所在城市出发后,在其旅途中恰好路过他所要去的每个城市1次,最后返回出发地,希望找到最优路线,使得所走的路线总长度最短.旅行售货商问题为图论中的一个经典问题,是NP难的.文献[13]证明了给定$O(n)$条边、$O(wt(MST))$权值的t-支撑图,可以在$O(wt(MST))$时间内给出旅行售货商问题的t近似算法.
(2) 支撑图用于压缩路由(compact routing)[14].在网络通信中路由至关重要,对于n个设备的网络,如果每个路由表的最大内存量随着节点数目n的增大是异步地、缓慢地增长的,则称路由模式是压缩的.也就是说,压缩路由倾向于在路由表规模和路径长度之间获得尽可能优化的平衡.支撑图的支撑比可以用来衡量路由的效率,反映了当前路由与可能最好的路由相比的近似率.支撑比与路由表大小之间的关系已被广泛研究,实际上,这是推动支撑图发展的原因之一.
(3) 支撑图用于度量空间搜索[15].度量空间搜索是通过距离函数进行向量之间相似性搜索的问题,在包括模式识别、多媒体数据库、图像检索等众多领域有着广泛需求.通常,搜索算法时间开销很大,一种可行的方法是计算每两个对象的距离并存储起来,这样会提高时间效率,但需要大量额外的存储空间.可以采用支撑图作为稀疏数据结构来减少存储.
(4) 支撑图用于线性系统.如果输出相对于输入是线性关系,那么这个系统就是线性系统,或者是指能抽象成线性系统数学模型的系统.文献[16]用支撑图思想抽象线性系统的输入,得到比较好的近似结果,主要使用的是支撑树(森林).
(5) 支撑图甚至可以用于生物科学中蛋白质的可视化(protein visualization)[17],抽象出蛋白质的骨干结构,简化蛋白质折叠轨迹的全部或部分可视化过程.
本文主要讨论支撑图在无线网络拓扑控制中的应用.支撑图在无线网络拓扑控制中起着重要的作用,因为支撑图不仅保持了原网络通信图的连通性,而且每一对节点间距离都是原通信图中最短距离的常数因子倍.更好的是,支撑图中只有线性数目条边,但这也可以构造满足其他拓扑需求.无线网络拓扑控制时,保持拓扑图有一定的支撑性,有助于更好地设计路由协议、减少能量消耗、减小网络延迟,从而延长网络寿命.若想充分理解无线网络拓扑控制和支撑图之间紧密的联系,参见文献[18].
文献[19]首次在无线网络拓扑控制中引入支撑图,文中研究的是单位圆盘图(unit disk graph,简称UDG)的支撑图,分析了UDG的常见子图的能量支撑比,如RNG(relative neighborhood graph)为n-1,GG(Gabriel graph)为1,YG(Yao graph)为O(1),给出了常数节点度,常数能量支撑比的支撑图构造算法.RNG等邻近图在支撑图研究中经常使用.RNG,GG可用于路由算法的拓扑构造,但它们最坏情形下的距离支撑比也很大.在无线网络背景下,研究的通常是UDG的支撑图.文献[20]给出的算法,能将所有(1+ε)-距离支撑图转换为UDG下的(1+ε)-支撑图.
与以往工作不同,本文关注的大多数算法所构造的支撑图,都是相应通信图的生成子图.也就是说,构造的这些支撑图的基础图是通信图,而不是通常意义下的几何图.在无线网络拓扑控制中使用支撑图,要结合需求设计合适的构造算法.首先,无线(ad hoc,传感器)网络通常节点众多,集中式算法通常需要掌握网络全局信息,而在网络规模较大的情况下获取全局信息将会消耗大量能量,不适用于资源受限的无线(ad hoc,传感器)网络.而在分布式,特别是局部化算法中,每个节点根据周围的局部信息,分布式并行地进行运算.因此局部算法不仅能够提高效率、节省能量,而且能够灵活适应网络拓扑的动态变化,更加适用于大规模、自组织的无线网络.当然,支撑图的集中式算法给了局部算法很多借鉴之处.其次,无线网络拓扑控制中使用的支撑图算法应该更好地考虑如上所述的稀疏性、有界度、小权值等拓扑特性;无线网络的这些需求也是近年来计算几何和图论领域支撑图理论发展的推动力;反之,计算几何和图论领域支撑图理论的发展也必定会推动无线网络中支撑图构造算法的发展.第三,能量消耗始终是无线网络节点通信重点关注的问题,因为节点通常只有有限电池供电或者难以更换能源,拓扑时会直接考虑保留能耗最小的路径,这就涉及到能量支撑图或者跳数支撑图(消息转发经过的节点少)的设计.最后,无线网络模型也在发展之中,如最近广泛研究的物理干扰模型,总结和分析原有的基于图的模型下没有考虑干扰、或者在协议干扰模型下提出的无线网络支撑图算法能够更好地在物理干扰模型下设计支撑图算法.
已有工作[8-10]大都侧重探讨几何支撑图,与它们相比,本文更侧重在无线网络环境下来讨论支撑图构造算法,构造的支撑图是通信图的生成子图,而不是一般几何图.本文中支撑图的分类、支撑图构造算法的分类也更全面,且对重要算法的性能进行了详细比较和分析.
本文第1节给出支撑图及相关的定义,并对支撑图进行详细分类.第2节归纳和比较近年来各种权值的无向支撑图在无线网络中的构造算法,主要讨论的是距离(几何)支撑图,着重比较和分析局部算法的性能.第3节考察有向支撑图构造算法,构造有向支撑图挑战性更大,但因为无线网络中节点的传输功率可能不一致,因此讨论有向支撑图很有必要.第4节依次讨论满足特定拓扑特性的支撑图构造算法.第5节总结全文,并展望下一步的研究工作.
1 网络模型及支撑图相关定义 1.1 网络模型定义1(通信图). 给定一个无线网络用图$G = (V,E)$表示,其中,V代表传感器节点集,如果当且仅当传感器节点u和v能够相互直接通信时,边${e_{uv}} = (u,v) \in E,$那么,G称为无线网络的通信图,${e_{uv}}$称为通信图中的一条边,或称为一个链接.
确定一个给定的节点u能够同另一个节点v进行通信的典型规则是,在v处接收的信号与噪声之比SNR(signal-to-noise ratio)必须大于或等于一个给定的门限值φ.假设采用确定的路径损耗传播模型,在发送节点和接收节点处满足全向天线,两个节点是连通的,当且仅当它们之间的距离r满足条件r < rc = (pt/${\varphi {\sigma ^2}}$)$^{1/\alpha }$其中Pt为发送功率,${\sigma ^2}$为附加的噪声功率(本文中两节点连通条件考虑了噪声功率${\sigma ^2}$),α为路径损耗指数,在2~6之间取值,距离${r_c}$通常称作传输范围.如果每个节点的传输功率相同,则所有节点的传输范围相同,相应的图模型
称为UDG[21],如图 1(a)所示.如果每个节点的传输功率不同,则所有节点的传输范围不同,相应的图模型称为圆盘图DG(disk graph),如图 1(b)所示.可推广至三维空间,三维空间中所有节点的传输范围相同的图模型称为UBG(unit ball graph),节点的传输范围不同的图模型称为BG(ball graph).当然还有其他变形,如拟单位圆盘图QUDG(quasi UDG)等.
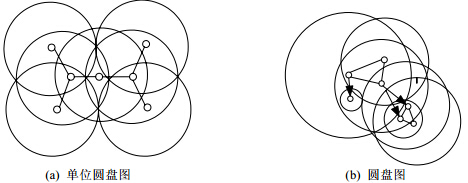 | Fig. 1 UDG and DG图 1 单位圆盘图和圆盘图 |
当发送端给其传输范围内的接收端发送信息时,因为信号传输之间存在干扰,接收端有可能无法成功接收信息.根据干扰的影响特性,常用的干扰模型分为两种,一种是协议干扰模型,另一种是物理干扰模型SINR (signal to interference-plus-noise ratio)[22].协议干扰模型可以理解为基于图的干扰模型,考虑的是成对的链路之间的干扰关系.在协议干扰模型中,节点v可以成功解码来自节点u的传输,当且仅当在接收者v的干扰范围内(通常大于传输范围)没有其他同时正在进行传输的链路.即协议干扰模型是一种二元干扰模型,两条链路之间要么互相干扰,要么不互相干扰.在构建干扰最优的拓扑结构时,可以采用文献[3]中给出的基于链路和基于节点的两种显式干扰定义.物理干扰模型考虑的是累加干扰,即使一条很远处的链路的传输也可能影响正在进行传输的链路成功通信.在物理干扰模型中,节点u和v之间的通信成功,当且仅当在v处接收的信号与干扰噪声比超过某个门限值,这个门限值依赖于信道的特征.因此物理干扰模型更实际,但更复杂.
1.2 支撑图定义及分类通信图通常是连通的,一般为赋权图.从节点u到节点v的费用函数$cost(u,v)$可以是两节点之间的欧氏距离$d(u,v),$此时的通信图为几何图;从节点u到节点v的费用函数$cost(u,v)$可以是节点u向节点v发送消息时所消耗的能量$d{(u,v)^\alpha },$, α为路径损耗指数;从节点u到节点v的费用函数$cost(u,v)$也可以表示为节点之间的跳数$d{(u,v)^0},$值为1.
定义2(t-支撑图(t-spanner)). 给定连通图$G = (V,E),$在G的生成子图$H = (V,{E_H})$中,令$cos{t_H}(u,v)$表示H中从节点u到节点v可能路径的最小费用函数.若对于V中任意节点对u,v,满足$cos{t_H}(u,v) \le t \cdot cos{t_G}(u,v),$实数$t \ge 1$,则称H为G的t-支撑图,称t为支撑比(stretch factor或spanning ratio),称u,v间满足上述条件的路径为t-支撑图路径.在计算几何背景下,连通图G可能是完全图;在无线网络背景下,连通图G是通信图,此时$cost(u,v)$代表从节点u到节点v假设能直接通信时的费用函数,而节点u和节点v之间可能因为超出彼此的传输范围没有边存在.
若$cost(u,v) = d(u,v),$则t称为距离支撑比,H称为距离支撑图或称为几何支撑图,图 2依次给出同一节点集合的UDG图和此UDG图的3个不同距离支撑比的支撑图;若$cost(u,v) = d{(u,v)^\alpha },$则t称为能量支撑比,H称为能量支撑图;若$cost(u,v) = d{(u,v)^0},$则t是跳数支撑比,H称为跳数支撑图.t有时记为1+ε,其中,ε>0,有大量文献构造了(1+ε)-支撑图.
 | Fig. 2 UDG and corresponding three different distance stretch factor spanners图 2 UDG与相应3个不同距离支撑比的支撑图 |
通信图通常为无向图,相应的支撑图也为无向支撑图.如果通信图为有向图,则相应的支撑图也为有向支撑图,原图和支撑图都是强连通图.
距离支撑图中有弱支撑图和强支撑图两种变形.如果$H = (V,{E_H})$中任意一对节点间在以u为圆心,以$t \cdot d(u,v)$为直径的圆盘内都有路径相连,则H称为G的弱t-支撑图,如图 3所示.如果$H = (V,{E_H})$中任意节点对u和v满足$H = (V,{E_H})$其中$cost(u,v) = d(u,v),$且u和v最短路径上所有边的长度都不大于$d(u,v),$则H称为G的强t-支撑图.
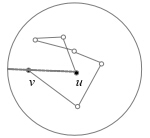 | Fig. 3 Weak distance spanner图 3 弱距离支撑图 |
强支撑图性质.如果H是完全几何图的平面强支撑图,那么H∩UDG就是相应UDG的平面支撑图[23].
若$cos{t_H}(u,v) \le cost(u,v) + c,$则H称为G的加性c-支撑图[24](additive stretch factor),c称为加性支撑比.
若$cos{t_H}(u,v) \le c \cdot cost(u,v) + d,$则H称为G的$(c,d)$支撑图[24].
如上所述,我们给出支撑图的如下分类:按照支撑比在形式上的变形,支撑图可分为比值支撑比支撑图、加性支撑比支撑图以及$cost(u,v)$支撑图;按照费用函数$cost(u,v)$的不同,可以分为距离支撑图、能量支撑图以及跳数支撑图;根据原始通信图中的边是否有方向,可以分别构造无向支撑图、有向支撑图;还可以构造考虑干扰的支撑图;距离支撑图中还有弱支撑图和强支撑图的变形.支撑图的分类如图 4所示.
 | Fig. 4 Taxonomy of spanners图 4 支撑图分类 |
邻近图定义为一个包含点集V和边集E的图,有向边(u,v)属于该图当且仅当点v位于点u的邻域内,这个邻域是在事先定义的邻近度量方法下产生的[25].下面给出常见邻近图的定义.
MST(minimum spanning tree):满足所有边的费用之和最小的生成树.
RNG(relative neighborhood graph):对$\forall u,v \in V,$若边$(u,v) \in $RNG,则不存在点w,使得$\max \{ d(u,w),d(v,w)\} < d(u,v).$
GG(Gabriel graph):对$\forall u,v \in V,$如果边$(u,v) \in $GG,则不存在点w,使得${d^2}(u,w) + {d^2}(v,w) < {d^2}(u,v).$
DTG(Delaunay triangulation graph):如果三角形∆uvw∈DTG,则这3个顶点的外接圆内不含任何其他点(G至少有不共线3点).
YG(Yao graph):以u为中心引n条射线将平面等分为k个锥形域,在每个锥形域内如果有其他点,则选择距离u最近的某点v,使有向边(u,v)∈YG,此时的YG用$\overrightarrow {YG} $表示;如果加入的是反向边(v,u),则称为reverse YG,用$\overleftarrow {YG} $表示;如果同时加入两方向的边,则称为YG.通常k≥6.
θ图:θ图与YG非常类似,不同之处只在于不是连接到每个锥形域中最近的节点,而是连接到每个锥形域轴线投影距离最短的节点[26].
邻近图的图例如图 5所示,邻近图的性质及与支撑图的关系见表 1.
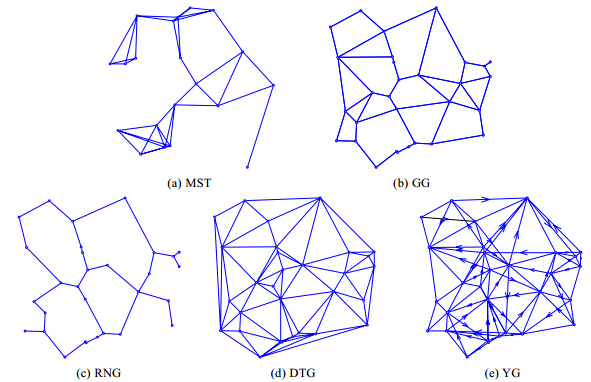 | Fig. 5 The proximity graph based UDG图 5 基于UDG的邻近图图例 |
| Table 1 Properties of the proximity graph 表 1 邻近图的性质 |
支撑图的类型有很多,支撑图构造算法更加复杂,计算有最少边的t-支撑图是NP难的[27, 28],即使计算有最小支撑比的生成树也是一个NP难问题[29].过去二三十年,有大量文献给出了不同的支撑图构造算法.根据网络拓扑是否预知,我们把支撑图的构造算法分为两大类,如图 6所示.集中式算法为无线网络中支撑图的构造提供了很多思路.但无线网络本身就是一个分布式系统,所以分布式算法更适用于无线网络,特别是局部算法.本节我们主要按照此分类标准把支撑图的构造算法梳理一下,主要讨论距离支撑图的构造算法.
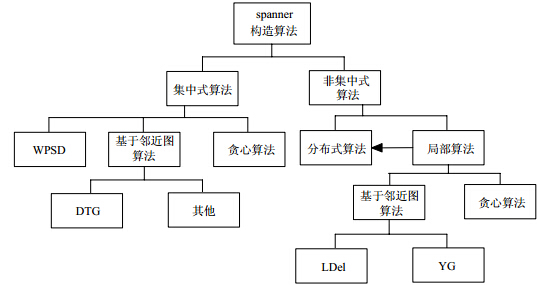 | Fig. 6 Taxonomy of spanner construction algorithm 图 6 支撑图构造算法分类 |
距离支撑图的集中式构造算法主要有3种,一是贪心构造算法,二是基于邻近图的构造算法,三是良分离成对分解(well-separated pair decomposition,简称WSPD)构造算法,后一种在无线网络中很少使用.下面我们主要讨论前两种算法.
1.贪心算法
使用贪心算法构造不同类型的t-支撑图,从节点u到节点v的费用函数$cost(u,v),$或为1代表跳数,或是两节点之间欧氏距离,或是从一个节点发送消息到另一个节点所需能量$cost(u,v).$
由于依据连通图G的点集V和边集E才能计算出所需权值,所以贪心算法的输入有连通图G和支撑比t.贪心算法PathGreedy是由最小生成树的Kruscal算法推广而来的,构造不同类型权值的t-支撑图的过程如下所示:首先计算连通图G中每条边的权值,所有的边按照权值非递减排列.初始化G的生成子图$H = (V,{E_H}),$其中,${E_H}$初始化为空集.算法依次处理所有边,对于每条不在${E_H}$中的边$(u,v) \in E,$PathGreedy算法检查在临时图H中的$cos{t_H}(u,v)$与$cost(u,v)$的比值,如果比t大,边就添加到集合${E_H}$中.可以证明,由PathGreedy构造的结果拓扑是相应度量的t-支撑图.
下面给出构造距离、能量、跳数支撑图的贪心构造算法[30].
算法1. PathGreedy.
输入:图G(V,E)支撑比t(t≥1);
输出:t-支撑图H(V,EH)
1: FOR 每条边$(u,v)$DO
2: 计算边上的费用函数$cost(u,v)$//可能为从节点u到节点v的距离,能量或者为1(跳数)
3: ENDFOR
4:按照费用函数$cost(u,v)$非递减排序
5:$H = (V,{E_H}),{E_H} = \emptyset ,$另设${E_T} = E$
6: WHILE ${E_T} \ne \emptyset $ DO
7: $(u,v) \leftarrow (u,v) \in {E_T}$且拥有最小费用函数
8: IF$cos{t_H}(u,v) > t \cdot cost(u,v)$
9: THEN ${E_H} = {E_H} \cup \{ (u,v)\} $
10: ${E_T}/(u,v)$//(u,v)处理结束, 从临时边集ET中去掉
11: ENDWHILE
PathGreedy算法中如果边以另一种顺序依次计算,就可以得到另一个拓扑.这种算法不能局部实现,因为它基于所有链路排序.
文献[30]中首先给出支撑图的贪心算法.贪心算法构造的t-支撑图有许多很好的性质,如每个节点的度有常数界(这样的支撑图只有线性数目的边)[31],并且贪心算法构造的支撑图的权值是同样节点集的MST权值的O(logn)倍[32],当原图为平面图时权值为1+O(1/t).但贪心算法执行时间复杂度为O(n3logn),因为图中节点对的数目是O(n2),每一对节点使用Dijkstra算法计算最短路径时间为O(nlogn).文献[33]改进了贪心算法,时间复杂度改进为O(n2logn).当原图G中节点限定在固定维数空间,边的距离采用欧氏距离时,贪心算法构造的支撑图是相应节点的MST权值的O(1)倍,边数为O(n)[34].
2.基于邻近图的算法
DTG是支撑图,它的支撑比有上下界.令DT(V)表示节点集合V的DTG,令VOR(V)表示节点集合V的Voronoi图.众所周知,DT(V)和VOR(V)是相互对偶的.给定两个点x和y(x∈V,y∈V),可按照下面方法在DT(V)内构造一条从x到y的路径,如图 7中粗线所示.为了简化阐述,假定x和y在同一水平线上,且x在y的左边,x,y节点间连一直线,依次与节点x,P1,P2,P3,…,Pk, y的Voronoi区域相交,记path(x,y)=xp1p2p3…pky我们称path(x, y)为一个Voronoi图路径,由DT(V)中的边组成.$path(x,y)$路径长度之和与节点x,y间欧氏距离的比值在一定范围内.若x,y不在一条水平线上,可以进行转化,因此DTG就是一个支撑图.文献[26]给出的DTG支撑比上界是$\frac{{4\sqrt 3 }}{9}{\rm{\pi }} \approx 2.418.$最近,文献[35]证明了更紧密的上界为1.998;文献[5]中猜想下界为$\frac{{\rm{\pi }}}{2}$,文献[36]给出了下界为1.584 6的证明.最近,文献[37]给出了更紧的下界为1.593 2,是大于$\frac{{\rm{\pi }}}{2}$的.Voronoi图可以使用分治法在O(nlogn)时间内构造,它的对偶图DTG也可在O(nlogn)内得到.
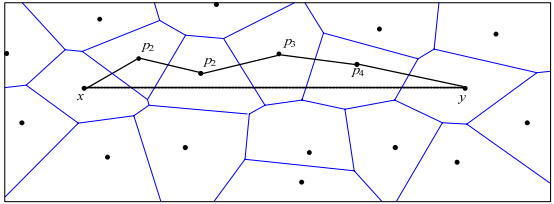 | Fig. 7 DTG and spanner图 7 DTG与支撑图 |
根据强支撑图性质,用构造完全几何图的平面强支撑图的方法,也能构造相应UDG的平面支撑图.Bose等人在文献[38]中首次证明可以构造一个完全几何图的强的平面支撑图,DTG是一个强$\frac{{4{\rm{\pi }}\sqrt 3 }}{9}$支撑图.他们将Keil和Gutwin在文献[26]中的证明方法推广,证明了DTG确实是一个强的支撑图.这意味着UDG和DTG的交集是UDG的平面支撑图.
DTG中三角形$\Delta uvw$的外接圆$disk(u,v,w),$不会包括DTG中其他节点,这称为DTG的空圆性质.空圆性质是证明DTG支撑比上下界的关键性质.可以将空圆性质定义为三角形每条边的一侧都有一个空的区域,这称为空邻域性质.当依据空邻域性质定义图中的边时,这个几何图就是一个邻近图.如RNG中边$(u,v)$在分别以u,v为圆心、|uv|为半径的两圆相交部分不会有其他顶点,GG中边$(u,v)$在以线段uv中点为圆心、|uv|为直径的圆内无其他节点.RNG,GG等邻近图支撑比的范围见表 1.Bose等人在文献[39]中给出了更多邻近图的支撑比上下界.
最近,文献[40]再次研究了Chew在文献[5]中研究过的L1度量Delaunay三角剖分构建的支撑图之支撑比, 给出了更紧密的上界为$\sqrt {4 + 2\sqrt 2 } \approx 2.61$;并且证明了${L_\infty }$度量的Delaunay三角剖分的上界也是$\sqrt {4 + 2\sqrt 2 } .$
2.1.2 局部算法在实际网络中,网络拓扑不可能完全可知,为此,集中式算法实际上是不可行的,需要根据具体的网络条件设计支撑图的分布式构造算法.如果该支撑图的分布式算法同时还是局部化(localized)的,则每个节点仅需根据邻居节点的信息就可以做出判断是否加入支撑图.这时的网络通信主要集中在各节点及其邻居节点之间的局部小范围内,有利于降低网络通信负荷,减少数据传输能量消耗.考虑到无线(ad hoc,传感器)网络规模巨大,而且网络拓扑结构会动态变化,因此分布式且局部化的算法比集中式算法更有利于网络扩展,灵活性更高.
局部算法是指只运行常数同步通信轮,算法中通信的跳数是一个常数,与网络中节点个数无关的分布式算法.其中通信轮定义为从发送一个消息到在接收端完整地处理完消息为止的一个时间段.换句话说,局部算法中,一个节点的输出是这个节点的常数半径范围内可用的邻居节点,即每个节点的状态仅依赖于它的k-跳邻居信息,与整个网络拓扑无关.对于任意一个正整数k,k称为局部算法的局部界(local horizon),对应着k-局部算法.令${N_k}(v)$={w|从v到w存在一条跳数不超过k的路}.在局部环境中,计算${N_k}(v)$比计算${N_{k - 1}}(v)$代价要大,因此,应尽可能地设计k比较小的k-局部算法.
1.YG和θ图
YG和θ图是以几何角度、距离同时作为约束条件的邻近图结构,适合用局部算法构建.YG构造中,如果中心节点有两个或者更多的最近邻居,可以任选一个邻居节点连接边或向所有的最近邻居节点连接边.最初的文献[41]使用前一个策略.
为了局部的计算YG,每个节点$u \in V$必须将其位置广播给所有的邻居.对于节点u接收的每条消息,计算发送节点v所在锥i.然后,将u和v之间距离与u和这个锥中目前为止发现的最近邻居${n_u}[i]$的距离进行比较.如果算法结束后,${n_u}[i]$则<u,v>表示节点u在锥i中选择的有向边.算法的伪代码如下.
算法2. Yao graph.
输入:图$G(V,E),$, c≥6
输出:$Y{G_c}(V,{E_H}).$
对于每个节点$u \in V,$
1: 初始化${n_u}[ ] = \emptyset ,$令其记录u在每个锥形域中的邻接点
2: 广播其位置信息
3: FOR每个接收到的消息(假设发送节点为v) DO
4: i←v所在的锥形域编号
5: IF ${n_u}[i] = \emptyset $或$d(u,{n_u}[i])$>$d(u,v)$//$d(u,v)$记录$uv$间距离
6: THEN ${n_u}[i] \leftarrow v$
7: ENDFOR
算法的时间复杂度为O(nlogn),每个节点处理时只需关注它的邻居节点,因此算法可以分布式地、局部地执行.上述算法产生的YG不是对称的,如图 8(a)所示.图中所有节点的传输范围都相同,记为rc;其中,c=8.YG中从u到v有弧并不意味着从v到u有弧.YG甚至只是弱连通的,即并不能保证任何节点对之间都有强连通路径.YG最大的节点入度为n-1.如果没有两个节点到其他节点的距离一样,或者说当中心节点有两个或者更多的最近邻居时,选其中一个节点连接边,则YG的出度是有界的.将上述算法得到的YG每条弧去掉方向,就得到双向YG又叫无向YG,如图 8(b)所示.YG是连通的,但不一定可平面.因为IEEE 802.11标准采用双向通信链路,所以通常使用无向YG,本文中YG一般指无向YG.当$c \ge 6$时,YG中给定节点对(x,y),每次取端点与y在同一锥形域中的边.按照此策略取到的路径记为$path(x,y) = x{p_1}{p_2}{p_3}...{p_k}y,$则$path(x,y)$路径长度之和与节点x,y间欧氏距离的比值小于等于1/(1-2sin(π/c))证明参见文献[19].文献[42]给出了常数距离支撑比和有界节点度的YG构造支撑图方法.显然,YG2和YG3都不是支撑图,在文献[43]中,YG4被证明是支撑比为$8\sqrt 2 (29 + 23\sqrt 2 )$的支撑图.最近,在文献[44]中证明了YG6的支撑比为5.8,对于c≥7的YGc文献[43]给出的支撑比为$1 + \sqrt {2 - 2\cos (2{\rm{\pi }}/c)} $文献[44]针对c≤5且c为奇数的情况,给出的支撑比更准确,为1/(1-2sin(3π/4)).
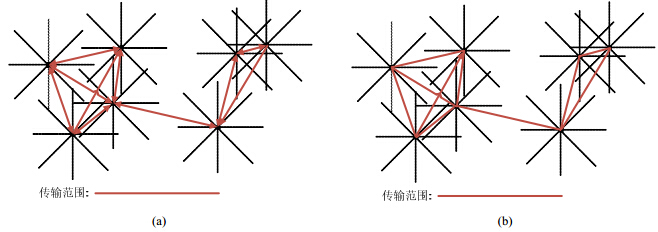 | Fig. 8 Directed graph YG8and corresponding undirected graph YG8图 8 有向图YG8和无向图YG8 |
θ图与YG有类似的性质.很长一段时间,对于$c > 6$的$Y{G_c}$和${\theta _c}$图(其中,$\theta = 2{\rm{\pi }}/c$)给出的距离支撑比为$1/(1 - 2\sin ({\rm{\pi }}/c)),$能量支撑比为1/${{{(1 - 2\sin ({\rm{\pi }}/c))}^\alpha }}$最近的研究结果证明,${\theta _2}$和${\theta _3}$不是支撑图,${\theta _4}$和${\theta _5}$分别在文献[45, 46]证明是支撑图,对于c>5的情形,令k≥1为整数,当c=4k+2时,支撑比为$1 + 2\sin (\theta /2)$[47],当c=4k+3或4k+5时,支撑比为${\cos (\theta /4)}$/${(\cos (\theta /2) - \sin (3\theta /4)}$), 当c=4k+4时,支撑比为${1 + 2\sin (\theta /2)}$/${(\cos (\theta /2) - \sin (\theta /2))}$[48].
2.LDel
大量文献在DTG的基础上,使用局部算法构造UDG的支撑图.令UDel(unit Delaunay triangulation)为UDG和DTG的交集,由强支撑图性质,则UDel是UDG的支撑图,支撑比上下界与DTG一样.Gao等人提出了一种局部算法[49],构造受限DTG图RDG(restricted Delaunay graph),这个平面图是UDel的母图(supergraph),显然是支撑图.在RDG中,每个节点u有边的集合$E(u)$. $E(u)$中的边满足:(1) 每条边最大为一个长度单位;(2) 边是对称的,即${e_{uv}} \in E(u)$当且仅当${e_{vu}} \in E(u);$(3) 得到的图是平面的;(4) 所有长度最大为1的DTG边保证在$E(u)$的并集中.该局部算法中每个节点只需运行常数通信轮,算法的消息复杂度是$O({n^2}).$
在文献[50]中,Li等人定义一个k-局部DTG三角形Δuvw,Δuvw的外接圆$disk(u,v,w)$不包含${N_k}(u),{N_k}(v),{N_k}(w)$的节点,其中${N_k}(u)$表示节点u的k跳内邻居,并且Δuvw所有边的长度都不超过单位长度.由k-局部DTG三角形构成的k-局部DTG,用LDel(k)(k-hops localized Delaunay graph)表示,图中包含所有长度最大为1的GG边和所有k-局部DTG三角形的边.Li等人证明,如果k≥2,LDel(k)是UDel的母图,并且是平面的.LDel(1)是非平面的,可通过移除LDel(1)中交叉的边(属于LDel(1)但不属于LDel(2)的边),构造平面支撑图,记为PLDel(planarize LDel).注意,PLDel是LDel(1)的子图,是LDel(2)的母图,也是UDG的支撑图.
在文献[50]中,Li等人提出了一种3-局部算法来计算PLDel,算法的消息复杂度为O(n).如果假定发送每个节点ID花费最多一个消息,则O(n)的常数最大为49.他们的算法需要4个通信轮.Araujo等人通过提出一种快速2-局部算法来计算PLDel[51],改进了Li等人的工作.他们的算法仅需要1个通信轮,且消息复杂度可以改进到11n.Bose等人的2-局部算法需要1个通信轮[52],且消息复杂度可以改进到5n.文献[53]也进行了相应的改进工作.
Wang和Li给出了3-局部算法构造UDG的平面支撑图[54],给出的支撑图节点度有界,最大为23.算法的消息复杂度为O(n).Kanj等人给出$\left\lfloor {(8/{\rm{\pi }}){{(\lambda + 1)}^2}} \right\rfloor $-局部算法[55],可以构造度为Δ的UDG的平面支撑图,其中,Δ≥14,λ>2.这两种算法都以LDel(2)算法为基础.文献[56]给出的LDel(2)构造算法,消息复杂度为O(n),其中O(n)的常数可能是几百,通信开销较大.
UDel的另一个子图PDT(partial delaunay triangulation)最近也被证明满足支撑特性[57],支撑比小于等于$\left\lfloor {(8/{\rm{\pi }}){{(\lambda + 1)}^2}} \right\rfloor $PDT也是UDG的支撑图,且适合局部算法构造.
在DTG的基础上构造支撑图的局部算法与DTG构造算法一样,对节点位置敏感.如果没有准确的位置信息,则会影响所得支撑图的可平面性等特性.
3.其他
文献[3]给出了基于发送者的显式干扰的模型,给出局部算法计算干扰最优的t-支撑图.算法采用贪心思想,且将寻求边${e_{uv}}$的干扰最优路径限制在t/2跳邻居区域,算法主要由3步组成:(1) 收集t/2邻居信息;(2) 按照贪心的策略计算每条边的最小干扰路径;(3) 通告路径上所有边保留在拓扑中.
Li等人在文献[58]以及Kanjet等人在文献[55]中提出的局部算法保证了支撑图中所有边的长度和至多是相应MST中所有边长度和的常数因子倍,文献[59]把文献[58]中的结果推广至拟单位圆盘图QUDG.
2.1.3 小 结通过以上对距离支撑图集中式、分布式算法,特别是局部算法的讨论,可以看出,集中式支撑图算法思想给局部算法的设计带来很多启发.而且距离支撑图的很多算法可以用于跳数、能量支撑图的设计.表 2给出以上算法的一个比较.
| Table 2 Comparison of the distance spanner construction algorithm 表 2 距离支撑图构造算法比较 |
文献[19]分析了UDG的常见子图的能量支撑比,如RNG为n-1,GG为1,YG为O(1),还利用YG思想给出了常节点度、常数能量支撑比的UDG的支撑图构造算法.文献[60]给出了能量支撑比为2的有界常节点度的能量支撑图构造算法.Li等人在文献[61, 62]中将YG与GG结合,给出一种构造${{{\sqrt 2 }^\alpha }}$/${(1 - {{(2\sqrt 2 \sin {\rm{\pi }}/k)}^\alpha })}$. 能量支撑图的算法,其中,k≥9,α为路径损耗因子,并且构造的支撑图是平面的、有界度的、边的总长度至多是相应最小生成树边总长度的常数因子倍.文献[63]改进了结果,给出了能量支撑图局部构造算法,支撑比为1+${(2\sin {\rm{\pi }}/k)^\alpha },$度有界k+5,其中,k≥10,并证明了该支撑比是接近最优的.Schindelhauer等人研究了弱支撑图、距离支撑图与能量支撑图之间的关系[64],证明了任意c-弱支撑图是${{{(8c + 1)}^d} \cdot {{(2c)}^\alpha }}$/${(1 - {2^{d - \alpha }})}$. 能量spanner,其中,d为维数,α为路径损耗指数.
2.3 跳数支撑图无线网络中高性能的路由算法需要低跳数支撑比的支撑图.文献[65]给出了常节点度的、平面的距离和跳数支撑图构造算法.Bose等人证明了GG图是UDG图的$\Omega (\sqrt n ) - $跳数支撑图和$\Theta (\sqrt n )$-距离支撑图[39],RNG图是UDG图的$\Theta (n)$-跳数支撑图和$\Theta (n)$-距离支撑图.文献[66]使用规则正方形网格划分节点形成簇,从而给出低跳数支撑比的、平面的支撑图构造算法.
3 有向支撑图构造算法第2节讨论的大都是无向支撑图构造算法.考虑每个节点有不同的传输范围,边有方向,也就是说,节点u能传输消息给v,并不意味着v也能传输消息给u.此时,通信图是有向的,传输范围不再是对称的.也就是说,有向图的支撑图是在有向圆盘图的基础上构造的.因此在无线网络拓扑控制中构造有向支撑图很有必要.有向支撑图算法会在无向支撑图的基础上加入考虑方向的特性.文献[6]指出,在有向图中构造spanner要比在无向图中构造spanner难得多,在某些有向图中根本不可能构造稀疏支撑图.例如,n个节点的完全二部图(X,Y,E)满足|X|=|Y|=n/2,并且所有的有向边都是从X到Y的,边数为O(n2),但任何子图都不是支撑图,如图 9所示.
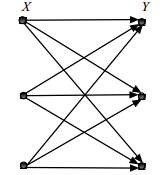 | Fig. 9 Directed complete bipartite graph G(X,Y,E)图 9 有向完全二部图G(X,Y,E) |
为了构造有向图的支撑图,试图把有向图中不对称的距离变得对称.Cowen和Wagner[67]引入了往返距离,u和v之间的往返距离定义为u到v的最短路径加上v到u的最短路径的距离.文献[68, 69]指出,应用此方法后,无向图中距离近似的一些方法就可以用于有向图.
在欧氏度量空间中,YG构造法稍作修改,可以构造O(nε-d)条边的有向(1+ε)-支撑图[41].另外,文献[20]也给出了在给定有向圆盘图上构造(1+ε)-支撑图的算法,算法如下:
算法3. Disk-Spanner.
输入:圆盘图$G(V,E)$, 任意小的正数ε;
输出:支撑图$H(V,{E_H}).$
1: ${E_H} \leftarrow \emptyset $
2: ${P_0} \leftarrow \emptyset $
3: FOR $i \leftarrow 0$ TO $\left\lfloor {{{\log }_{1 + \gamma }}M} \right\rfloor $ DO
4: FOR 每条边$(x,y) \in E({M_{i + 1}},{M_i})$ DO
5: IF $\left| {NN(x,{P_i})x} \right| > \gamma {M_{i + 1}}$
6: THEN ${P_i} \leftarrow {P_i} \cup \left\{ x \right\}$
7: IF 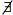 $(x',y) \in {E_H}$满足 $x' \in \Gamma (NN(x,{P_i}))$
$(x',y) \in {E_H}$满足 $x' \in \Gamma (NN(x,{P_i}))$
8: THEN ${E_H} \leftarrow {E_H} \cup \left\{ {(x,y)} \right\}$
9: ENDFOR
10: ${P_{i + 1}} \to {P_i}$
11: ENDFOR
算法Disk-Spanner中令$\gamma < \frac{\varepsilon }{6}$为固定小正数.首先将圆盘图$G(V,E)$中的(有向)边分为$i \in \left[ {0,\left\lfloor {{{\log }_{1 + \gamma }}M} \right\rfloor } \right]$个边类$E({M_{i + 1}},{M_i}),$其中,M为节点的最大传输范围,${M_i} = M/{(1 + \gamma )^i},{M_0} = M$是最大的传输范围,$E({M_{i + 1}},{M_i}) = \left\{ {(x,y)|{M_i}_{ + 1} \le \left| {xy} \right| \le {M_i}} \right\}$.在构造算法的每个阶段,i维护一个特殊节点集Pi,称为支点集.令x∈V,$NN(x,{P_i})$表示x在节点集Pi中最近邻居节点,则对于一个支点x满足$p \in {P_i}$也就是说,如果一个节点x在支点集Pi中的最近邻居为p,则x一定能传输消息到p.
假设在每个边类中边按照权值从小到大排序,从i=0开始,每个边类中的边按照非递减顺序依次进行如下处理:假设当前处理的边为(x,y),如果$NN(x,{P_i})$到x的距离$\left| {NN(x,{P_i})x} \right| > \gamma {M_{i + 1}},$则x加入支点集Pi,边(x,y)加入边集EH,如果$\left| {NN(x,{P_i})x} \right| \le \gamma {M_{i + 1}}$且不存在边$(x',y) \in {E_H}$满足$x' \in \Gamma (NN(x,{P_i})),$则边(x,y)加入边集EH.
文献[20]证明了算法的输出是(1+ε)-支撑图,并且证明所得支撑图拥有$O(n{\varepsilon ^{ - d}}\log M)$条边,其中,M为最大传输半径;算法的执行时间为$O(m\log n)$,m为圆盘图中边的数目.将边按长度分类构造有向支撑图的思想对后继研究有很大的借鉴意义.
文献[70]对Disk-Spanner算法稍加改进,证明了常数加倍度量(doubling metric)空间中,有向支撑图的规模不会与M无关.在加倍度量空间中,每一个球B至多可以被半径为球B半径一半的2d个球所覆盖,d为常数.该文中将传输半径稍加松弛,即r;=(1+ε)r,可以构造出O(nε-d)条边的(1+ε)-支撑图.
在有向支撑图中,找到边数最少的t-支撑图也一直是一个值得研究的问题,令t为节点总数n的函数,当t=$\Omega (\log n)$时,得到的结论非常有实用价值.该问题是Peleg等人在文献[6]中提出的,并指出这一问题是NP-难的.文献[71]使用线性规划松弛技术研究有向支撑图,对于所有t≥1的有向t-支撑图设计了$\widetilde O({n^{2/3}})$近似算法,也就是边数为最优有向t-支撑图的$\widetilde O({n^{2/3}})$倍,这是任意边长度支撑图的首个次线性近似算法.文献[71]还在单位边长度下,在t≥4时改进了现有的$\widetilde O({n^{1 - 1/t}})$近似[72];对于t=3的特殊情况,设计了一种不同算法实现了$O(\sqrt n )$近似,改进了现有的$\widetilde O({n^{2/3}})$近似[72, 73].
4 满足某特性支撑图构造算法这一章将依次讨论满足特定拓扑特性的支撑图构造算法,如低权重、常数度、动态的、容错的以及考虑干扰的支撑图构造算法.
4.1 低权重支撑图通信图的权值定义为所有边上的权值之和.构造权值最小的距离支撑图是NP难的[74],但是,为了节省信息传输所需能量,构造权值尽可能小的支撑图始终是追求的目标之一.支撑图的权值通常以相应的MST权值来衡量.
贪心算法是构造低权值支撑图的典型算法(参见第2.1.1节).文献[30]使用贪心算法给出了构造有${n^{1 + 1/k}}$条边的(2k-1)-支撑图,对边的数目和支撑比进行折中,贪心算法的缺点是执行时间长.文献[75]采用两路的网络流算法,可构造(2k-1)(1+ε)-支撑图,具有$O(k$·${n^{1 + 1/k}})$条边,权值是相应节点的MST权值的$O(k$·${n^{1/k}})$,倍,执行时间为O(k·m+min(n·log n,m·a(n)))其中,α(n)为Ackermann反函数,运行时间好于文献[30].
接下来讨论以能量作为权值时,总能量消耗最优的支撑图的构造算法.UDG的GG子图是能量支撑比为1的支撑图,很自然地可以想到,使用UDG的GG子图中边的子集可以得到总能耗最优的支撑图,但事实不是这样,文献[76]给出了例子.支撑图的一般构造算法都不能用于设计总能量消耗最优的支撑图,因为大多数算法都是针对无向图的,而设计总能耗最优的支撑图应该将最大功率时得到的通信图,进行功率重分配.因此需要采用不对称模型,属于有向支撑图范畴.而有向支撑图的文献,大多没有关注权值特性,然而权值与总能量消耗关系很大.
保证连通的总能量最优问题就是NP难的[77],再加上考虑支撑比特性更难.文献[76]首次将支撑图特性与最小化能量消耗关联在一起.然而作者只是给出了两种启发性算法,未给出理论证明的界.文献[78]在支撑比t∈{1,2}时,针对能量支撑图和距离支撑图提出了功率分配方法,能取得总能耗和支撑比的折中;k>2时,分析了文献[79]中提出的功率分配方案,给出了相应的能量支撑图和距离支撑图支撑比的界.文献[80]进一步改进了能量支撑图中的总能量消耗近似比.
4.2 有界度支撑图一个节点的邻居节点个数称为这个节点的度.支撑图中节点度的最大值,称为支撑图的度.若支撑图的节点平均度是常数,则图中边的数目是节点的线性倍.支撑图度有界,则每个节点的通信负载不会过大,网络不容易拥塞.此外,局部广播消息和设计紧缩路由协议时[14],也是支撑图的度决定了使用的存储空间大小.因此设计有界度支撑图是支撑图构造算法目标之一.
支撑图研究过程中一直比较关注度的问题,参见第2节.但解决支撑图的最大节点度问题在技术上一直是一个巨大的挑战[81].大多数有界度支撑图构造的基础是DTG和YG,通常的想法是先构造DTG,然后再采取步骤得到既保持支撑特性且度有界的子图,采用的方法通常是抽取DTG的YG子图,有时也可能会再增加额外边来保持支撑特性.文献[82]通过有目的地去掉DTG的一些边,给出最大度为7的强${(1 + \sqrt 2 )^2} \times T$-支撑图,运行时间为$O(n\log n)$,其中,T为原DTG的支撑比,且${(1 + \sqrt 2 )^2} \times T < 14.1.$文献[83]通过解决YG入度无界的问题,构造度有界的支撑图.由YG最初构造过程可知,$Y{G_c}$出度为c,而入度无界.可以将$Y{G_c}$每个扇区中只保留最短的入边,得到度有界的$Y{Y_c}$图.文献[83]证明,当k≥6时,$Y{Y_{6k}}$是支撑比为11.67的支撑图.当k≥8时,$Y{Y_{6k}}$支撑比降为4.75.
文献[84]给出了“处处稀疏”的提法,即不仅要求构造的支撑图规模要小,而且要求最大节点度也要小.该文主要研究了2-支撑图的有界度问题(lowest degree 2-spanner,简称LD2S),建立了LD2S和稠密k-子图的变形问题形式上的联系,给出两个问题线性规划描述的强松弛,采用“可信任的”随机舍入技术,即要求所有顶点和边的选择概率与它们的线性规划值成比例.主要的贡献在于设计了LD2S问题多项式时间的$\tilde O({\Delta ^{3 - 2\sqrt 2 }}) \approx \tilde O({\Delta ^{0.172}})$近似算法,其中,Δ是输入图的最大度,改进了之前的LD2S问题的$\tilde {\rm O}({\Delta ^{1/4}})$近似算法[85].
4.3 动态支撑图大多数支撑图构造算法,工作在固定节点集合V上.在一些应用环境中,需要从V增加或者删除一些节点,对于无线网络设计更是如此.节点每次更新时,不希望都重新构造支撑图.所以研究动态的支撑图非常有必要.Gao等人在文献[86]中首次研究动态支撑图,给出了构造规模为O(n/εd)的(1+e)-支撑图的算法,其中辅助存储结构的更新时间取决于α(V),α(V)是点集P的扩散速度,定义为点对之间的最大距离和最小距离的比,确切的更新时间为O(logα(V)/εd),之后的文献[87]改进了这一结果,能构造规模为O(n/εO(d))、更新时间为O(logn/εO(d))的支撑图,其中,d为点集所在空间的维数.
Gao等人在文献[86]中给出了运动支撑图的一个变形问题,P集中点沿着连续的轨迹移动.分子动力学和移动网络研究会涉及这样的问题.文献[88]进一步研究了该问题,假设${R^d}$维空间的点沿着有界度多项式的轨迹运动,给出了构造规模为O(n/εd-1)、最大度为O(logdn)的支撑图构造算法,其中,构造动态支撑图使用的辅助结构大小为O(nlogdn),点变化时相应时间为O(logd+1n),当支撑图拓扑需要变化时,可以在O(logn)的时间内更新完毕.
4.4 容错性支撑图无线网络需要容错性:一些节点失效后,无论网络中剩下什么,支撑结构必须还是有效的.网络的容错性与图的连通性密切相关,容错网络要求高度连通.图的顶点(边)连通性定义为使图变得不连通的最少顶点(边)数.网络的容错性影响网络的可靠性.
距离支撑图的容错度概念首先出现在文献[89]及后续文献[90]中.容错网络的目标是,当小数目的节点(或边)失效后,剩余的网络仍然保持支撑图特性,也就是说,每对节点间仍然有t-支撑图路径.图H(V,EH)中,令H\S表示顶点集为V\S的H导出子图,如果对于所有子集SÍV,其中,|S|≤k,满足H\S依然是顶点集V\S的t-支撑图,则H是k顶点容错的t-支撑图.k边容错与k顶点容错定义类似,所不同的只是集合SÍE.显然,当k=0时,就是原先的t-支撑图.
文献[89, 90]证明,当讨论容错的支撑图时,只考虑顶点容错的支撑图就可以了,因为边容错的支撑图很容易转换为顶点容错的支撑图.文中还提供了简单算法可以把任何支撑图H通过合理添加边构造容错的支撑图H;,如果Δ是H的最大节点度,k是顶点容错度,则H;的度为$O({\Delta ^{k + 1}})$,权值是H的权值和的$O(k{\Delta ^k})$倍.文献[91]改进了文献[89]中的结果,利用θ图的支撑图构造算法,构造$O(kn)$条边的k容错支撑图,且利用θ图变形,加上汇聚节点,构造度为$O({k^2})$的k容错支撑图.文献[92]中将贪心构造支撑图的算法变形,构建度为O(k)、权值为$O({k^2})$倍最小生成树权值的k容错支撑图.文献[93]中引入功率分配,得到满足能量支撑图特性和容错性的拓扑图.
在支撑图中,找到拥有最少边数的t-支撑图H是非常重要的,对于容错的支撑图同样如此.文献[94]给出的构造k-容错的(2t-1)-支撑图算法,得到的支撑图中边的数目为$O({k^3}{t^{k + 1}} \cdot {n^{1 + 1/t}}{\log ^{1 - 1/t}}n).$对于支撑比t≥3,文献[95]设计了简单的转化方法,能够把每个至多为f(n)条边的t-支撑图转化为至多为$O({k^3}\log n).f(2n/k)$条边的k容错t-支撑图,与支撑比t无关.在支撑图的标准贪心构造算法中应用上述方法,能够实现$O\left( {{k^2}{n^{1 + \frac{2}{{t + 1}}}}} \right)$条边的k容错t-支撑图.
k顶点容错的支撑图必须保证在k个节点都失效后,图至少还连通.这就意味着,每个节点的度至少为k+1,则图中边的条数至少为(k+1)n/2.当k值变大时,图就变成稠密图.这是我们不希望出现的情形.
文献[96]中提出了f(r)鲁棒性t-支撑图.对于图H(V,EH),子集SÍV,令H\S表示顶点集为V\S的H导出子图.如果对于任何子集SÍV,存在超集S+ÊS,满足|S|≤r,且|S+|≤f(|S|),使得H\S是V\S+的t-支撑图,则图H称为f(r)鲁棒性t-支撑图.
支撑图的鲁棒性与容错性有关,但这是两个不同的概念.只有满足f(r)= 的容错支撑图才是一个f(r)鲁棒性支撑图.f(r)鲁棒性支撑图的优点是存在稀疏的f(r)鲁棒性支撑图.文献[96]中给出的一维节点集例子,是$O(n\log n)$条边的$O(r\log r)$鲁棒性的1-支撑图,满足任何$O(n/\log n)$节点失效后,余下的$n - o(n)$个节点依然是1-支撑图.而k=n/logn的k容错支撑图若满足此特性,至少有Ω(n2/logn)条边.
的容错支撑图才是一个f(r)鲁棒性支撑图.f(r)鲁棒性支撑图的优点是存在稀疏的f(r)鲁棒性支撑图.文献[96]中给出的一维节点集例子,是$O(n\log n)$条边的$O(r\log r)$鲁棒性的1-支撑图,满足任何$O(n/\log n)$节点失效后,余下的$n - o(n)$个节点依然是1-支撑图.而k=n/logn的k容错支撑图若满足此特性,至少有Ω(n2/logn)条边.
使用容错性支撑图的应用场景,使用鲁棒性支撑图会是更好的选择.但是,支撑图的鲁棒性概念刚被提出,实际应用于无线网络仍有很多工作要做.
4.5 考虑干扰的支撑图无线网络中大部分的支撑图构造算法都是在图模型下构造的,如UDG,DG等等,只考虑了节点通信的连通条件.但节点间的干扰是避免不了的,节点或者链路之间的干扰使得一些符合连通条件的链路可能无法进行传输.协议干扰模型和物理干扰模型是基于干扰的影响来建模无线网络的.协议干扰模型考虑的是链路对之间的干扰,而物理干扰模型考虑的是累加干扰,更为复杂.
最初考虑减少干扰的思路是,构造的支撑图越稀疏,干扰就会越小.Burkhart等人给出了反例[3],并在协议干扰模型中基于发送者给出了显式的干扰定义,即给出在一个给定的链路上通信所影响的节点的数目,还给出了在t/2跳内构造干扰最优的t-支撑图的局部算法.
文献[97]给出了物理干扰模型下贪心调度算法,称为MaxSINR,基本思想是用贪心算法依次填充每一个时隙,使得每个时隙的最小SINR是最大化的.MaxSINR算法一个接一个地将传输添加到结果图中,每个传输检查是否对于满足拓扑特性要求是必需的.若不是必需的,就从未处理的传输队列中移除.最后,结果图中的每个时隙中所有的传输都满足SINR条件,可以被有效调度,也满足特定的拓扑特性,如支撑图特性.这样就给出了一种在物理干扰模型下构造支撑图的思路,但这种思路无疑是很耗费时间的,只存在理论上的意义.
文献[98]利用局部广播、常数密度控制集和最远邻居树给出了物理干扰模型下的构造MST的分布式近似算法[99].提出并证明了一种算法,可以在物理干扰模型下,在Olog(n)的时间内使得n个点的网络强连通.所有这些研究有助于物理干扰模型下支撑图构造算法的研究.
4.6 综合考虑各拓扑特性的支撑图本节以上讨论的文献,侧重于考虑某一拓扑特性的支撑图构造,但也会兼顾其他拓扑特性.最近涌现出一批最新文献,综合考虑了支撑图的支撑比、规模、权值、度、直径、容错度和运行时间.文献[100]从权值为常数的哈密尔顿路径开始构造支撑图,同时使用了文献[101]给出的常数节点度、对数直径和权值的1-支撑图构造算法.文献[102]给出了类似思路,但算法开始采用的是Net-Tree而不是哈密尔顿路径.文献[100, 102]的构造算法各有优缺点,哈密尔顿路径有常数权值,但是节点间距离可能变得很长,使得支撑图的直径可能变得很大.而文献[102]中能控制Net-Tree中节点间距离,但是Net-Tree的权值可能变成对数的.两种方法都未能解决有界节点度问题.文献[103]采用了有界度支撑图构造算法中使用的隐含树,这样得到的支撑图自然是有界度的,并且算法容易扩展得到一个容错的支撑图.文献[104]进一步改进了结果.表 3给出了以上文献结果的一个比较.
| Table 3 Comparison of the spanner construction algorithm with one or more topology properties 表 3 考虑多个拓扑特性的支撑图构造算法比较 |
无线网络拓扑控制时,保持拓扑图有一定的支撑性,对于设计路由协议、减少能量消耗、减小网络延迟以及延长网络寿命,是很有必要的.自从支撑图概念被提出,针对几何应用环境和网络应用环境,于是提出了大量的支撑图构造算法.集中式算法中,贪心算法构造的支撑图有很好的拓扑特性,稀疏、常数节点度、权值小,但执行的时间长;基于邻近图的构造算法执行时间短,但支撑比有特定的上界和下界.
在实际网络中,网络规模大,整个网络拓扑不可能完全可知,因此需要根据需求设计支撑图的分布式构造算法,特别希望设计常数轮执行时间的局部算法,若此,一个节点执行时只需考虑它周围k跳的邻居即可.有大量文献将集中式算法转化为局部算法,参见第2.1.2节.
无线网络拓扑控制中支撑图设计时,应根据需要满足一定的拓扑特性要求,如规模小、权值小、度小,有一定的容错性和鲁棒性等,因此涌现出大量文献着重构造某一特性或综合考虑各拓扑特性的支撑图.
本文对支撑图的研究成果进行了详细讨论,对无线网络拓扑控制中支撑图构造算法进行了分析和比较.但是通过无线网络拓扑控制中支撑图的构造算法分析可以看出,仍然存在许多挑战性的问题亟待研究.
继续寻找分布式的、局部的算法解决支撑图的相关问题
在无线网络中,集中式算法实际上是不可行的,继续寻找性能更优的、分布式的、局部的算法解决支撑图的相关问题是一个重要而又基本的问题.将集中式算法转化为局部算法的基本思路是,每个节点只考虑其k跳内的邻居,只在k跳内通信,得到局部最优的结果,最后通过详细证明和仿真验证所得到的图具有支撑图性质.局部算法中每个节点只运行常数通信轮,局部算法的主要性能指标是消息复杂度和位复杂度.研究消息复杂度或位复杂度更优的支撑图局部算法,相应的通信开销会降低.
非UDG中支撑图的构造
实际中网络不一定是平面的,可能是三维立体的,因此将可构造支撑图的算法扩展到三维空间中进行研究.在实际网络中所有节点的传输范围不一定相同.此时,一个无线网络可以模型化为一个有向图,有向图中非对称的链路能被更有效地调度,而在有向图中构造支撑图的算法并不多.研究中,以借鉴和采用UDG模型中优秀的支撑图构造思想和算法类型,并结合实际网络模型的特点进行算法的设计,以确保算法的正确性和优越性.
带干扰的支撑图构造算法
在无线网络中,拓扑控制是节省能量的一种有效方法,但是当一个网络拓扑中存在大量干扰时,节点发送的很多信号就会受到干扰、数据将会延迟,甚至丢失.因此在多种网络模型和干扰模型中构造干扰感知的分布式支撑图算法也是我们研究的一个主要内容.在基于节点的显式干扰模型中构造支撑图是一个有待解决的问题,也有意义,因为使用图的拓扑控制解决这个问题有助于物理干扰模型下的调度.物理干扰模型是更实际的干扰模型,如何结合不断涌现的物理干扰模型下进行拓扑的新思想、新方法构造支撑图也是亟需研究的问题.
同时满足多个拓扑特性的支撑图构造算法
构造拥有最少边数的支撑图是支撑图研究中的基本问题,也是最近研究非常活跃的一个领域.要求构造的支撑图拥有最少边数,就是希望规模小.现在构造的支撑图不仅希望规模小,还希望尽量拥有常数度、权值小等特性.从而支撑图的构造算法就可以转化为多目标优化问题,并转化为数学规划问题来解决,利用松弛、网络流等技术更好地对支撑图算法的这些特性进行优化和折中.
容错及鲁棒性
在无线网络中,节点失效是不可忽视的问题,因此支撑图构造的拓扑也容易失效,除非构造的支撑图有足够的容错性和鲁棒性.
在对该问题进行研究时,还应同时考虑支撑图的其他特性,而不是一味地追求容错或节能.最优容错机制的设计问题还远未得到解决,人们对容错性和鲁棒性的理解还不够,尤其是鲁棒性这一概念刚被提出来,还没有其他相应研究成果;其次,与此相关的算法还需要进一步研究和完善.
移动无线网络模型中支撑图的构造
无线网络拓扑是变化的、不可预知的,因此,支撑拓扑图的维持和修复就变得非常重要.现有的大多数支撑图构造协议都只考虑规模、度等参数性能,而不能在网络拓扑发生改变时维持以前的支撑图.即当节点移动时,要么缺少合理的机制来处理节点的移动,要么需要较长的时间周期性地进行整个支撑图的重构造.因此,寻找移动网络模型中新的支撑图构造算法,在不引入太多通信开销的情况下有效地构造并维持较小规模的支撑图是非常重要的.维持网络中支撑图的方法通常有两种:重构网络的整个支撑图和局部修复.研究时可分单个节点移动和多个节点同时移动、或者控制节点移动和非控制节点移动、节点沿一定轨迹移动和节点随机移动来分别加以分析.在研究该问题构造新的适合移动网络的支撑图算法时,需要综合考虑拓扑的其他特性及修复支撑图的时间和信息开销问题.
支撑图问题本身比连通性、支配集、生成树等问题要复杂,存储量大,运行时间长,如何找到更简单、性能更好的算法,会一直是该领域的研究热点.另外,还应将图论中支撑图的研究新成果与更实际的网络模型(如物理干扰模型、衰落模型等)相结合,使支撑图能够更好地应用于无线网络.
| [1] | Takagi H, Kleinrock L. Optimal transmission ranges for randomly distributed packet radio terminals. IEEE Trans. on Communications, 1984,32(3):246-257 . |
| [2] | Wagner D, Wattenhofer R. Algorithms for Sensor and Ad Hoc Networks: Advanced Lectures. Heidelberg: Springer-Verlag, 2007. 81-98 . |
| [3] | Von Rickenbach P, Wattenhofer R, Zollinger A. Algorithmic models of interference in wireless ad hoc and sensor networks. IEEE/ACM Trans. on Networking (TON), 2009,17(1):172-185 . |
| [4] | Siraj S, Gupta A, Badgujar R. Network simulation tools survey. Int’l Journal of Advanced Research in Computer and Communication Engineering, 2012,1(4):201-209. |
| [5] | Chew LP. There is a planar graph almost as good as the complete graph. In: Proc. of the 2nd Symp. on Computational Geometry. New York: ACM Press, 1986. 169-177 . |
| [6] | Peleg D, Schäffer AA. Graph spanners. Journal of Graph Theory, 1989,13(1):99-116 . |
| [7] | Peleg D, Ullman JD. An optimal synchronizer for the hypercube. SIAM Journal on Computing, 1989,18(4):740-747 . |
| [8] | Narasimhan G, Smid M. Geometric Spanner Networks. New York: Cambridge University Press, 2007. |
| [9] | Bose P, Smid M. On plane geometric spanners: A survey and open problems. Computational Geometry Theory and Application, 2013,46(7):818-830 . |
| [10] | Kanj I. Geometric spanners: Recent results and open directions. In: Proc. of the 3rd Int’l Conf. on Communications and Information Technology. Beirut: IEEE Computer Society Press, 2013. 78-82 . |
| [11] | Levcopoulos C, Lingas A. There are planar graphs almost as good as the complete graphs and almost as cheap as minimum spanning trees. Algorithmica, 1992,8(3):251-256. |
| [12] | Bartal Y, Gottlieb L, Krauthgamer R. The traveling salesman problem: Low-Dimensionality implies a polynomial time approximation scheme. In: Proc. of the 44th Annual ACM Symp. on Theory of Computing (STOC 2012). New York: ACM Press, 2012. 663-672 . |
| [13] | Rao SB, Smith WD. Approximating geometrical graphs via “spanners” and “banyans”. In: Proc. of the 30th Annual ACM Symp. on Theory of Computing (STOC’98). New York: ACM Press, 1998. 540-550 . |
| [14] | Gavoille C, Sommer C. Sparse spanners vs. compact routing. In: Proc. of the 23rd ACM Symp. on Parallelism in Algorithms and Architectures (SPAA 2011). New York: ACM Press, 2011. 225-234 . |
| [15] | Navarro G, Paredes R, Chávez E. t-Spanners for metric space searching. Data & Knowledge Engineering, 2007,63(3):820-854 . |
| [16] | Elkin M, Emek Y, Spielman D, Teng S. Lower-Stretch spanning trees. SIAM Journal on Computing, 2008,38(2):608-628 . |
| [17] | Russel D, Guibas L. Exploring protein folding trajectories using geometric spanners. In: Altman RB, Dunker AK, Hunter L, Jung TA, Klein TE, eds. Proc. of the Pacific Symp. on Biocomputing. Hawaii: World Scientific, 2005. 40-51. |
| [18] | Rajaraman R. Topology control and routing in ad hoc networks: A survey. ACM SIGACT News, 2002,33(2):60-73 . |
| [19] | Li X. Wan P, Wang Y. Power efficient and sparse spanner for wireless ad hoc networks. In: Proc. of the Computer Communications and Networks. Scottsdale: IEEE Computer Society Press, 2001. 564-567 . |
| [20] | Peleg D, Roditty L. Localized spanner construction for ad hoc networks with variable transmission range. In: Proc. of the 7th Int’l Conf. onAd-Hoc Networks and Wireless (AdHoc-NOW 2008). Sophia Antipolis: Springer-Verlag, 2008. 135-147 . |
| [21] | Yu J, Wang N, Wang G, Yu D. Connected dominating sets in wireless ad hoc and sensor networks—A comprehensive survey. Computer Communications, 2013,36:121-134 . |
| [22] | Cardieri P. Modeling interference in wireless ad hoc networks. IEEE Communications Surveys & Tutorials, 2010,12(4):551-572 . |
| [23] | Bose P, Carmi P, Couture M, Smid M, Xu D. On a family of strong geometric spanners that admit local routing strategies. In: Dehne F, Sack J R, Zeh N, eds. Algorithms and Data Structures (WADS 2007). Heidelberg: Springer-Verlag, 2007. 300-311 . |
| [24] | Baswana S, Kavitha T, Mehlhorn K, Pettie S. Additive spanners and (a,b)-spanners. ACM Trans. on Algorithms, 2010,7(1): Article No.5 . |
| [25] | Lu G, Zhou M, Niu X, She K, Tang Y, Qin K. A survey of proximity graphs in wireless networks. Ruan Jian Xue Bao/Journal of Software, 2008,19(4):888-911(in Chinese with English abstract). http://www.jos.org.cn/1000-9825/19/888.htm |
| [26] | Keil JM, Gutwin CA. Classes of graphs which approximate the complete Euclidean graph. Discrete & Computational Geometry, 1992,7(1):13-28. |
| [27] | Klein R, Kutz M. Computing geometric minimum-dilation graphs is NP-hard. In: Kaufmann M, Wagner D, eds. GD 2006. Karlsruhe: Springer-Verlag, 2007. 196-207 . |
| [28] | Dinitz M, Kortsarz G, Raz R. Label cover instances with large girth and the hardness of approximating basic k-spanner. In: Proc. of the 36th Int’l Colloquium on Automata, Languages and Programming. Rhodes: Springer-Verlag, 2012. 290-301 . |
| [29] | Cheong O, Haverkort H, Lee M. Computing a minimum-dilation spanning tree is NP-hard. Computational Geometry, 2008,41(3): 188-205 . |
| [30] | Althöfer I, Das G, Dobkin D, Joseph D, Soares J. On sparse spanners of weighted graphs. Discrete & Computational Geometry, 1993,9(1):81-100 . |
| [31] | Soares J. Approximating Euclidean distances by small degree graphs. Discrete & Computational Geometry, 1994,11(1):213-233 . |
| [32] | Chandra B, Das G, Narasimhan G, Soares J. New sparseness results on graph spanners. In: Proc. of the 8th Annual Symp. onComputational Geometry (SoCG’92). Berlin: ACM Press, 1992. 192-201. http://dl.acm.org/citation.cfm?id=142675.142717&coll=DL&dl=ACM&CFID=492233736&CFTOKEN=26305933 |
| [33] | Bose P, Carmi P, Farshi M, Maheshwari A, Smid M. Computing the greedy spanner in near-quadratic time. Algorithmica, 2010, 58(3):711-729 . |
| [34] | Das G, Narasimhan G, Salowe J. A new way to weigh malnourished Euclidean graphs. In: Proc. of the 6th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA’95). San Francisco: ACM Press, 1995. 215-222. |
| [35] | Xia G. The stretch factor of the Delaunay triangulation is less than 1.998. SIAM Journal on Computing, 2013,42(4):1620-1659 . |
| [36] | Bose P, Devroye L, Löffler M, Snoeyink J, Verma V. Almost all Delaunay triangulations have stretch factor greater than p/2. Computational Geometry: Theory and Applications, 2011,44:121-127 . |
| [37] | Xia G, Zhang L. Toward the tight bound of the stretch factor of Delaunay triangulations. In: Proc. of the 23rd Annual Canadian Conf. on Computational Geometry (CCCG 2011). Toronto: Carleton University Press, 2011. |
| [38] | Bose P, Maheshwari A, Narasimhan G, Smid M, Zeh N. Approximating geometric bottleneck shortest paths. Computational Geometry: Theory and Applications, 2004,29(3):233-249 . |
| [39] | Bose P, Devroye L, Evans W, and Kirkpatrick D. On the spanning ratio of Gabriel graphs and β-skeleton. SIAM Journal on Discrete Mathematics, 2006,20(2):412-427 . |
| [40] | Bonichon N, Gavoille C, Hanusse N, Perković L. The stretch factor of L1- and L∞-Delaunay triangulations. In: Proc. of the European Symp. on Algorithms (ESA 2012). Ljubljana: Springer-Verlag, 2012. 205-216 . |
| [41] | Yao AC. On constructing minimum spanning trees in k-dimensional spaces and related problems. SIAM Journal on Computing, 1982,11(4):721-736 . |
| [42] | Arya S, Das G, Mount DM, Salowe J, Smid M. Euclidean spanners: Short, thin, and lanky. In: Proc. of the 27th Annual ACM Symp. on Theory of Computing (STOC’95). New York: ACM Press, 1995. 489-498. |
| [43] | Bose P, Damian M, Douïeb K, O’Rourke J, Seamone B, Smid M, Wuhrer S. p/2-angle Yao graphs are spanners. Int’l Journal of Computational Geometry & Applications, 2012,22(1):61-82 . |
| [44] | Barba L, Bose P, Damian M, Fagerberg R, Keng WL, O’Rourke J, van Renssen A, Taslakian P, Verdonschot S, Xia G. New and improved spanning ratios for Yao graphs. In: Proc. of the ACM Symp. on Computational Geometry (SoCG 2014). Kyoto: ACM Press, 2014. 30-39 . |
| [45] | Barba L, Bose P, De Carufel J, van Renssen A, Verdonschot S. On the stretch factor of the Theta-4 graph. In: Proc. of the Int’l Workshop on Algorithms and Data Structures Symp. (WADS 2013). London: Springer-Verlag, 2013. 109-120 . |
| [46] | Bose P, Morin P, van Renssen A, Verdonschot S. The θ5-graph is a spanner. In: Brandstädt A, Jansen K, Reischuk R, eds. Proc. of the WG 2013. Heidelberg: Springer-Verlag, 2013. 100-114 . |
| [47] | Bose P, De Carufel J, Morin P, van Renssen A, Verdonschot S. Optimal bounds on theta-graphs: More is not always better. In: Proc. of the 24th Canadian Conf. on Computational Geometry (CCCG 2012). Charlottetown: Carleton University Press, 2012. 305-310. |
| [48] | Bose P, van Renssen A, Verdonschot S. On the spanning ratio of Theta-Graphs. In: Proc. of the Int’l Workshop on Algorithms and Data Structures Symp. (WADS 2013). London: Springer-Verlag, 2013. 182-194 . |
| [49] | Gao J, Guibas L, Hershberger J, Zhang L, Zhu A. Geometric spanners for routing in mobile networks. IEEE Journal on Selected Areas in Communications, 2005,23(1):174-185 . |
| [50] | Li X, Calinescu G, Wan P, Wang Y. Localized Delaunay triangulation with application in ad hoc wireless networks. IEEE Trans. on Parallel and Distributed Systems, 2003,14(10):1035-1047 . |
| [51] | Araújo F, Rodrigues L. Fast localized Delaunay triangulation. In: Proc. of the 8th Int’l Conf. on Principles of Distributed Systems (OPODIS 2004). Grenoble: Springer-Verlag, 2005. 81-93 . |
| [52] | Bose P, Carmi P, Smid M, Xu D. Communication-Efficient construction of the plane localized Delaunay graph. In: Proc. of the 9th Latin American Theoretical Informatics Symp. Theoretical Informatics. Oaxaca: Springer-Verlag, 2010. 282-293 . |
| [53] | Chen Z, Xu P, Deng X. A distributed planar t-spanner topology control algorithm in wireless sensor networks. Journal of Computer Research and Development, 2012,49(3):529-540 . |
| [54] | Wang Y, Li X. Localized construction of bounded degree and planar spanner for wireless ad hoc networks. Mobile Networks and Applications, 2006,11(2):161-175 . |
| [55] | Kanj IA, Perković L, Xia G. Computing lightweight spanners locally. In: Proc. of the 22nd Int’l Symp. on Distributed Computing (DISC 2008). Arcachon: Springer-Verlag, 2008. 365-378 . |
| [56] | Calinescu G. Computing 2-hop neighborhoods in ad hoc wireless networks. In: Proc. of the Int’l Conf. on Ad-Hoc Networks and Wireless (AdHoc-NOW 2003). Montreal: Springer-Verlag, 2003. 175-186 . |
| [57] | Neumann F, Frey H. On the spanning ratio of partial Delaunay triangulation. In: Proc. of the 9th IEEE Int’l Conf. on Mobile Ad-Hoc and Sensor Systems (MASS 2012). Las Vegas: IEEE, 2012. 434-442 . |
| [58] | Li X, Wang Y, Song W. Applications of k-local MST for topology control and broadcasting in wireless ad hoc networks. IEEE Trans. on Parallel and Distributed Systems, 2004,15(12):1057-1069 . |
| [59] | Chávez E, Dobrev S, Kranakis E, Opatrny J, Stacho L, Urrutia J. Local construction of planar spanners in unit disk graphs with irregular transmission ranges. In: Proc. of the 7th Latin American Theoretical Informatics Symp. Valdivia: Springer-Verlag, 2006. 286-297 . |
| [60] | Wang Y, Li X, Frieder O. Distributed spanners with bounded degree for wireless ad hoc networks. Int’l Journal of Foundations of Computer Science, 2003,14(2):183-200 . |
| [61] | Song W, Wang Y, Li X, Frieder O. Localized algorithms for energy efficient topology in wireless ad hoc networks. Mobile Networks and Applications, 2005,10(6):911-923 . |
| [62] | Li X, Song W, Wang W. A unified energy-efficient topology for unicast and broadcast. In: Proc. of the 11th Annual Int’l Conf. on Mobile Computing and Networking (MobiCom 2005). Chicago: ACM Press, 2005. 1-15 . |
| [63] | Kanj IA, Perkovic L, Xia G. Local construction of near-optimal power spanners for wireless ad hoc networks. IEEE Trans. on Mobile Computing, 2009,8(4):460-474 . |
| [64] | Schindelhauer C, Volbert K, Ziegler M. Geometric spanners with applications in wireless networks. Computational Geometry: Theory and Applications, 2007,36(3):197-214 . |
| [65] | Alzoubi K, Li X , Wang Y, Wan P, Frieder O. Geometric spanners for wireless ad hoc networks. IEEE Trans. on Parallel and Distributed Systems, 2003,14(4):408-421 . |
| [66] | Catusse N, Chepoi V, Vaxès Y. Planar hop spanners for unit disk graphs. In: Scheideler C, ed. Algorithms for Sensor Systems. Heidelberg: Springer-Verlag, 2010. 16-30 . |
| [67] | Cowen LJ, Wagner CG. Compact roundtrip routing for digraphs. In: Proc. of the 10th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA’99). Philadelphia: ACM Press, 1999. 885-886. |
| [68] | Cowen LJ, Wagner CG. Compact roundtrip routing in directed networks. Journal of Algorithms, 2004,50(1):79-95 . |
| [69] | Roditty I, Thorup M, Zwick U. Roundtrip spanners and roundtrip routing in directed graphs. ACM Trans. on Algorithms, 2008, 4(3):Article No.29 . |
| [70] | Peleg D, Roditty L. Relaxed spanners for directed disk graphs. Algorithmica, 2013,65(1):146-158 . |
| [71] | Dinitz M, Krauthgamer R. Directed spanners via flow-based linear programs. In: Proc. of the 43rd Annual ACM Symp. on Theory of Computing (STOC 2011). San Jose: ACM Press, 2011. 323-332 . |
| [72] | Bhattacharyya A, Grigorescu E, Jung K, Raskhodnikova S, Woodru D. Transitive-Closure spanners. SIAM Journal on Computing, 2012,41(6):1380-1425 . |
| [73] | Elkin M, Peleg D. Approximating k-spanner problems for k>2. Theoretical Computer Science, 2005,337(1):249-277 . |
| [74] | Carmi P, Chaitman-Yerushalmi L. Minimum weight Euclidean t-spanner is NP-Hard. Journal of Discrete Algorithms, 2013,22: 30-42 . |
| [75] | Elkin M, Solomon S. Fast constructions of light-weight spanners for general graphs. In: Proc. of the 24th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA 2013). New Orleans: ACM Press, 2013. 513-525 . |
| [76] | Wang Y, Li X. Minimum power assignment in wireless ad hoc networks with spanner property. Journal of Combinatorial Optimization, 2006,11(1):99-112 . |
| [77] | Chen W, Huang N. The strongly connecting problem on multihop packet radio networks. IEEE Trans. on Communications, 1989, 37(3):293-295 . |
| [78] | Segal M, Shpungin H. Improved multi-criteria spanners for ad-hoc networks under energy and distance metrics. In: Proc. of the IEEE Int’l Conf. on Computer Communications (INFOCOM). San Diego: IEEE, 2010. 1-5 . |
| [79] | Carmi P, Segal M, Katz MJ, Shpungin H. Fault-Tolerant power assignment and backbone in wireless networks. Ad Hoc & Sensor Wireless Networks, 2007,4(4):355-366 . |
| [80] | Abu-Affash AK, Aschner R, Carmi P, Katz MJ. Minimum power energy spanners in wireless ad hoc networks. Wireless Networks, 2011,17(5):1251-1258 . |
| [81] | Bose P, Fagerberg R, van Renssen A, Verdonschot S. On plane constrained bounded-degree spanners. In: Proc. of the Latin American Theoretical Informatics Symp. Theoretical Informatics. Arequipa: Springer-Verlag, 2012. 85-96 . |
| [82] | Bose P, Carmi P, Chaitman-Yerushalmi L. On bounded degree plane strong geometric spanners. Journal of Discrete Algorithms, 2012,15:16-31 . |
| [83] | Bauer M, Damian M. An infinite class of Sparse-Yao spanners. In: Proc. of the 24th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA 2013). New Orleans: ACM Press, 2013. 184-196 . |
| [84] | Chlamtáč E, Dinitz M, Krauthgamer R. Everywhere-Sparse spanners via dense subgraphs. In: Proc. of the 53rd Annual IEEE Symp. on Foundations of Computer Science (FOCS 2012). New Brunswick: IEEE, 2012. 758-767 . |
| [85] | Kortsarz G, Peleg D. Generating low-degree 2-spanners. SIAM Journal on Computing, 1998,27(5):1438-1456 . |
| [86] | Gao J, Guibas LJ, Nguyen A. Deformable spanners and applications. Computational Geometry, 2006,35(1):2-19 . |
| [87] | Gottlieb LA, Roditty L. Improved algorithms for fully dynamic geometric spanners and geometric routing. In: Proc. of the 19th Annual ACM-SIAM Symp. on Discrete Algorithms (SODA 2008). San Francisco: ACM Press, 2008. 591-600. |
| [88] | Abam MA, de Berg M, Gudmundsson J. Kinetic spanners in Rd. Discrete & Computational Geometry, 2011,45(4):723-736 . |
| [89] | Levcopoulos C, Narasimhan G, Smid M. Efficient algorithms for constructing fault-tolerant geometric spanners. In: Proc. of the 30th Annual ACM Symp. on Theory of Computing (STOC’98). Dallas: ACM Press, 1998. 186-195 . |
| [90] | Levcopoulos C, Narasimhan G, Smid M. Improved algorithms for constructing fault-tolerant spanners. Algorithmica, 2002,32(1): 144-156 . |
| [91] | Lukovszki T. New results on fault tolerant geometric spanners. In: Proc. of the Int’l Workshop on Algorithms and Data Structures Symp. (WADS’99). London: Springer-Verlag, 1999. 193-204 . |
| [92] | Czumaj A, Zhao H. Fault-Tolerant geometric spanners. Discrete & Computational Geometry, 2004,32:207-230 |
| [93] | Shpungin H, Segal M. Near-Optimal multicriteria spanner constructions in wireless ad hoc networks. IEEE/ACM Trans. on Networking, 2010,18(6):1963-1976 . |
| [94] | Chechik S, Langberg M, Peleg D, Roditty L. Fault tolerant spanners for general graphs. SIAM Journal on Computing, 2010,39(7): 3403-3423 . |
| [95] | Dinitz M, Krauthgamer R. Fault-Tolerant spanners: Better and simpler. In: Proc. of the 30th Annual ACM Symp. on Principles of Distributed Computing (PODC). New York: ACM Press, 2011. 169-178 . |
| [96] | Bose P, Dujmović V, Morin P, Smid M. Robust geometric spanners. SIAM Journal on Computing, 2013,42(4):1720-1736 . |
| [97] | Völker M. Scheduling and topology control in wireless sensor networks [Ph.D. Thesis]. Karlsruhe: University of Karlsruhe, 2008. |
| [98] | Khan M, Kumar VS, Pandurangan G, Pei G. Brief announcement: A fast distributed approximation algorithm for minimum spanning trees in the SINR model. In: Proc. of the 26th Int’l Symp. on Distributed Computing (DISC 2012). Salvador: Springer- Verlag, 2012. 409-410 . |
| [99] | Halldórsson MM, Mitra P. Wireless connectivity and capacity. In: Proc. of the 23rd Annual ACM-SIAM Symp. on Discrete Algorithms (SODA 2012). Kyoto: ACM Press, 2012. 516-526 . |
| [100] | Elkin M, Solomon S. Optimal Euclidean spanners: Really short, thin and lanky. In: Proc. of the 45th ACM Symp. on Theory of Computing (STOC 2013). Palo Alto: ACM Press, 2013. 645-654 . |
| [101] | Solomon S, Elkin M. Balancing degree, diameter and weight in Euclidean spanners. SIAM Journal on Discrete Mathematics, 2014, 28(3):1173-1198 . |
| [102] | Chan THH, Li M, Ning L. Incubators vs. zombies: Fault-Tolerant, short, thin and lanky spanners for doubling metrics. 2012, 7. http://arxiv.org/abs/1207.0892 |
| [103] | Solomon S. Fault-Tolerant spanners for doubling metrics: Better and simpler. 2012, 7. http://arxiv.org/abs/1207.7040 |
| [104] | Solomon S. From hierarchical partitions to hierarchical covers: Optimal fault-tolerant spanners for doubling metrics. In: Proc. of the 46th ACM Symp. on Theory of Computing (STOC 2014). New York: ACM Press, 2014. 363-372 . |
| [25] | 路纲,周明天,牛新征,佘堃,唐勇,秦科.无线网络邻近图综述.软件学报,2008,19(4):888-911. http://www.jos.org.cn/1000-9825/19/ 888.htm |
| [53] | 陈志刚,徐鹏飞,邓晓衡.无线传感器网络中的分布式平面t-支撑拓扑控制算法.计算机研究与发展,2012,49(3):529-540. |
 2015, Vol. 26
2015, Vol. 26


