2. 符号计算与知识工程教育部重点实验室(吉林大学), 吉林 长春 130012
2. Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education(Jilin University), Changchun 130012, China
命题可满足问题(propositional satisfiability problem,简称SAT)是人工智能领域的热点问题,国内外研究人员对其做了大量工作并取得了显著成果[1, 2, 3, 4].随着SAT问题研究的日益成熟,其成果被广泛应用于其他领域,如在智能规划领域将规划问题编译成SAT问题,并利用高效的SAT求解器进行求解,在国际智能规划竞赛中一度取得优异的成绩,屡获冠军[5, 6, 7].SAT问题也同样被应用于求解基于模型的诊断问题[8],并取得了较好效果.SAT问题是NP完全问题[9],对于其他NP完全问题,几乎都可以转化成SAT问题进行求解.
#SAT是SAT问题的一种扩展问题,它的计算复杂性高于NP完全,属于#P完全的[10].人工智能研究领域存在着许多其他问题,如贝叶斯网络推理问题[11]、概率规划问题[12],在其转化成命题公式集合进行求解过程中,仅仅判断它们是否是可满足的是不够的,还需要知道它们的可满足赋值的数目,即模型个数.这种需要计算给定命题公式集合的模型个数的问题就是#SAT问题,如何高效地解决#SAT问题,对人工智能的很多领域都有深远意义.
近年来,#SAT问题受到国内外学者广泛关注.早在1991年,Dubois提出通过计算独立子句对应的模型个数来求解模型计数问题的方法[13].Zhang在1996年从理论角度对Dubois基于独立子句的方法进行了分析[14],随着问题规模的增大,算法的时间复杂度呈指数级增长.此后,Birnbaum和Lozinskii提出了基于Davis-Putnam过程的模型计数算法CDP[15].在CDP算法中,若公式中有单元子句,则先对单元子句进行处理从而化简公式;否则,随机选择一个变量a,将给定公式$\Phi $分成两个模型交集为空的子公式($\Phi $∧a)和($\Phi $∧⌉a),再分别求解.目前,求解#SAT问题的算法多数都是以CDP为基础的,如Bayardo和Pehoushek在CDP算法基础上加入组件思想,并提出Relsat算法[16].此算法中,CNF公式用约束图表示:图中的节点为出现在公式中的变量,若两个变量出现在同一子句中,则在图中代表这两个变量的节点之间就存在一条边.而各个独立的约束图可以看成是相互独立的组件,从而将公式分成多个子公式分别独立求解.Sang等人设计的Cachet系统[17, 18]同时使用了组件缓存和子句学习两种策略,通过记录已经计算过的组件结果,避免在后续的计算过程中重复之前的工作,是一种利用空间换时间的方法.Thurley在Cachet算法基础上,利用不同的存储方式提高了算法的空间利用率[19].
基于扩展规则的定理证明方法[20]已经得到了许多相关研究人员的重视,如:将扩展规则改进应用到模态逻辑的自动定理证明中[21];将扩展规则方法用于模型计数(model counting)问题[22],结合扩展规则的知识编译方法[23];对基于扩展规则方法进行改进,提出NER,SER和IBOHMH_IER等系列算法[24, 25, 26].
殷明浩等人将扩展规则方法推广到#SAT问题求解中,提出了一种CER方法[27].与传统的模型计数求解方法需要找出哪些赋值是给定子句集的模型不同,该方法需要找出不是子句集模型的赋值,可以看作是目前其他求解#SAT问题方法的一种补方法.CER方法的基本思想如下:对于给定的子句集,赋值与极大项之间存在一一对应的关系,一个赋值使得子句集为真当且仅当它的非形式的极大项不能被扩展出来,即,不能被扩展出的极大项与子句集的模型是一一对应的.基于这种对应关系,只要计算出不能被扩展的极大项个数,就能得到模型个数.然而要想得到不能被扩展的极大项个数,首先就需要计算出能被扩展出的极大项个数.这种求解模型计数的方法受到互补因子的影响,当互补因子较高时,该方法一般要优于基于归结的方法;反之,当互补因子较低时,要差于基于归结的方法.
本文在充分分析CER方法的基础上对其进行改进,给出增量求解的RCER方法.CER方法在求解子句集所能扩展出的极大项个数时,没有充分利用各计算项之间的关系来避免冗余计算.针对此问题,本文给出适合增量求解的重构CER方法.
1. 预备知识本节首先介绍#SAT问题的相关定义和概念,然后介绍扩展规则及其相关概念.首先,对在本文中使用的一些符号给出如下定义:xi(i=1,2,…,m)表示布尔变量;X={x1,x2,...,xm}表示变量集合;在子句中,用xi表示与变量xi对应的正文字,⌉xi表示变量xi的负文字;Ci(i=1,2,…,n)表示子句,由文字的析取构成,可将其看成是文字的集合; $\Phi $,$\Phi $'表示CNF公式,由子句的合取构成,可将其看成是子句的集合.
1.1 #SAT问题SAT问题又称命题可满足性问题,即,判定一个给定的命题公式是否可满足,其形式化定义如下:
定义1[28]. 对于一个给定的命题公式$\Phi $,SAT问题即判断是否存在一组赋值使得公式$\Phi $的值为真:若存在,则称公式$\Phi $是可满足的;否则,是不可满足的.
对于SAT问题,只要找到一组使给定命题公式为真的赋值,就可以确定它是可满足的.而#SAT问题是要找出所有这样赋值,定义如下:
定义2[28].对于一个给定的命题公式$\Phi $,#SAT问题是指计算出所有使命题公式$\Phi $为真的赋值个数.
一般地,称使命题公式为真的一组赋值为它的一个模型,所以#SAT问题也被称为模型计数问题.显然,模型计数问题的计算复杂性要高于命题可满足性问题.
1.2 扩展规则本节给出扩展规则及其相关的概念,扩展规则是归结原理的逆向推理规则,其定义如下:
定义3[20]. 对于一个给定的子句C和一个变量集合X,且在子句C中出现的变量包含于变量集合X,则有子句集合D={C∨x,C∨⌉x|x$ \in $X并且x的正负文字都不出现在子句C中},把C到D中元素的推导过程叫做扩展规则,D中的元素叫做子句C应用扩展规则的结果.
例1:给定变量集合{x1,x2,x3}和子句x1∨x2,那么对子句x1∨x2应用扩展规则的结果就是{x1∨x2∨x3,x1∨x2∨⌉x3}.
定理1给出子句C与其应用扩展规则后的结果D之间的关系.
定理1[20]. 子句C及其扩展后的结果D是等价的.
对一个子句集中的每个子句应用扩展规则,这样可以得到一个新的子句集.由定理1可得,应用扩展规则得到的子句集和原有的子句集是等价的.
当对该子句集循环不断应用扩展规则时,即:对子句集中每个子句应用扩展规则得到一个新的子句集,再对这个新子句集中的子句继续应用扩展规则,一直循环这样的操作,最后将得到一个不再变化的子句集.即,其中的子句已经无法再应用扩展规则扩展出新的子句.
例2:当子句集$\Phi $中只含有两个子句x1∨x2和x1∨x2∨⌉x3,变量集合X={x1,x2,x3},而对子句集$\Phi $应用扩展规则后,得到的最终子句集$\Phi $'={x1∨x2∨x3,x1∨x2∨⌉x3},其中,若对$\Phi $'中的子句再应用扩展规则已不能再得出新的子句.称子句集$\Phi $'中这样不能再被扩展的子句为极大项,其具体定义如下:
定义4[27]. 一个非重言式子句是变量集合X上的极大项当且仅当它包含变量集合X上所有变量的正文字或其负文字.
例3:给定变量集合X={x1,x2,x3},则子句x1∨x2∨x3和x1∨x2∨⌉x3是集合X上的两个极大项,而x1∨x2则不是.
2. 基于扩展规则的#SAT求解方法定理2[20]. 给定一个子句集$\Phi $、变量集合X,若$\Phi $中的子句都是X上的极大项,则子句集$\Phi $不可满足当且仅当$\Phi $中含有2|X|个互不相同的子句(|X|表示集合X中变量个数).
由定理2可得:对于一个不可满足的子句集$\Phi $,对其应用扩展规则后得到的与其等价的新的子句集$\Phi $'中含有且只含有2|X|个子句,即2|X|个极大项.然而对于这样的一个子句集$\Phi $',它的所有赋值个数也为2|X|,而且这些赋值都使其为假.其实,任意子句集上的所有赋值都是与其变量集合上的极大项一一对应的.
例4:对于变量集合X={x1,x2,x3}上的每个极大项,在图1的树中都存在一条赋值分支与其相对应,并使极大项为假.当一个子句集包含所有极大项时,其对应的任意一组赋值都会使其中的一个极大项为假,从而使整个子句集为假.
然而,#SAT问题是求出子句集的模型个数,对于不可满足的子句集,其模型个数为0.下面给出模型计数求解的基本定理:
定理3[27]. 给定一个子句集$\Phi $、变量集合X,若$\Phi $中的子句都是X上的极大项,则子句集$\Phi $的模型个数为2|X|-S,其中,S是$\Phi $中子句个数(S≤2|X|).
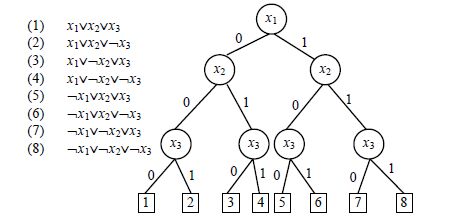
|
图1 变量集合X={x1,x2,x3}上极大项与赋值关系图 Fig.1 Relation of maximum terms and assignments on X={x1,x2,x3} |
定理2和定理3给出了赋值与极大项的对应关系.对于每个赋值,如果它使得子句集为真,那么在此赋值上为假的极大项不包含在子句集可扩展出的极大项中.所以,要计算一个子句集的模型个数,可先求出该子句集应用扩展规则后扩展出的极大项个数S,再根据定理3,即可得到子句集的模型个数2|X|-S.
当求解一个子句集扩展后得到的所有极大项个数时,直接将它们全部都扩展出来复杂度较高,且最坏情况下的其复杂性呈指数级增长.实际上,不需要将全部极大项都扩展出来就能得到它们的个数.
定理4[20]. 两个子句扩展出的极大项集合不含交集当且仅当这两个子句含有互补对.
互补对是同一变量的正负文字,由定理4可得:含有同一变量不同文字的两个子句扩展出的极大项集合不含交集,即,交集为空.
定理5(容斥原理)[29]. 集合A1,A2,…,An并集的元素个数可以用如下公式计算:
$\left| \bigcup\limits_{i=1}^{n}{{{A}_{i}}} \right|=\sum\limits_{i=1}^{n}{|{{A}_{i}}|}-\sum\limits_{1\le i<j\le n}{|{{A}_{i}}\cap {{A}_{j}}|}+...+{{(-1)}^{n+1}}|{{A}_{1}}\cap {{A}_{2}}\cap ...\cap {{A}_{n}}|$
对一个子句集应用扩展规则后,得到只包含极大项的新子句集,是原子句集中所有子句分别应用扩展规则后得到与其等价的极大项集合的并集.因此,可以利用容斥原理来求解其包含极大项的个数,易得到以下公式:
$\begin{align}
& S=\sum\limits_{i=1}^{n}{|{{P}_{i}}|}-\sum\limits_{1\le i<j\le n}{|{{P}_{i}}\cap {{P}_{j}}|}+ \\
& \sum\limits_{1\le i<j<l\le n}{|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|}-...+{{(-1)}^{n-1}}|{{P}_{1}}\cap {{P}_{2}}\cap ...\cap {{P}_{n}}| \\
\end{align}$
(1)
其中,$|{{P}_{i}}|={{2}^{|X|-|{{C}_{i}}|}},|{{P}_{i}}\cap {{P}_{j}}|=\left\{ \begin{array}{*{35}{l}} 0,\text{ }{{C}_{i}}\text{和}{{C}_{j}}\text{中含有互补文字}~ \\ {{2}^{|X|-|{{C}_{i}}\cup {{C}_{j}}|}},\text{ }{{C}_{i}}\text{和}{{C}_{j}}\text{中不含有互补文字} \\ \end{array} \right.$.
上式中,S表示子句集$\Phi $={C1,C2,…,Cn}应用扩展规则后所能生成的极大项个数,Pi表示子句Ci应用扩展规则后得到的与其等价的极大项集合,|Ci|表示子句Ci包含文字数量,|X|表示变量集合X中变量个数.
基于公式(1),可得一个子句集所能扩展出的极大项个数S,再根据定理3,可以求解得出子句集的模型个数,即2|X|-S.CER方法结合了变量赋值与极大项之间的对应关系以及子句与其应用扩展规则后得到的极大项集合之间的等价关系,进而利用子句集中已有子句来求解模型个数.
3. 结合扩展规则重构的#SAT增量求解方法上一节介绍了CER算法的基本思想,它与基于DP过程的求解#SAT问题方法不同,首先利用公式计算子句集所能扩展出的极大项个数S,然后即可得到模型个数为2|X|-S.然而,该方法在求解子句集所能扩展出的极大项个数时,没有充分利用公式(1)中各计算项之间的关系来避免冗余计算.针对此问题,本文给出适合增量求解基于CER的重构方法,下面先给出CER的重构方法和相关证明,随后给出计算极大项个数和子句互补判定的增量求解方法.
3.1 公式重构定义5. 对于两个子句,称它们是互补子句当且仅当它们至少含有一对互补文字.
定义6. 称一个包含多个子句的子句集是广义互补的当且仅当子句集中至少含有一对互补子句.
显然,定义5是定义6的一种特殊情况,定义6是定义5的扩展形式.由定理4可得:对于一对互补子句,它们所对应的极大项集合交集为空.下面给出定理4的扩展定理:
定理6. 给定子句集,若它是广义互补的,则其包含的所有子句扩展出的极大项集合交集为空集.
证明:由定义6可知:假设给定子句集包含子句C1,C2,…,Cn,若它是广义互补的,那么所有子句中至少含有一对互补子句.假设为Ci,Cj,则由定理4可知,Pi与Pj的交集为空.而由集合的性质可知:对于P1,P2,…,Pn,它们的交集必是其中任意两个集合交集的子集;特殊地,也必是Pi与Pj的交集的子集,故P1,P2,…,Pn的交集也为空集.
显然,当给定子句集中含有的互补子句较多时,公式(1)中值为0的计算项较多,从而此时这种基于扩展规则的方法效率一般较高.为了衡量给定子句集中互补子句的多少,下面给出互补因子的概念.
定义7[20]. 给定一个子句集$\Phi $={C1,C2,…,Cn},互补因子(complementary factor)是子句集中互补子句对个数与所有子句对个数之比,即T/(n*(n-1)/2),其中,T表示互补子句对的个数.
CER方法在求解时未能考虑公式(1)中各计算项之间的扩展关系,下面给出重构CER方法中关于各计算项间扩展关系的相关定义.
定义8. 称公式(1)中形如${{P}_{{{i}_{1}}}}\cap {{P}_{{{i}_{2}}}}\cap ...\cap {{P}_{{{i}_{h}}}}$的公式为极大项相交集,用字母Q表示,$|{{P}_{{{i}_{1}}}}\cap {{P}_{{{i}_{2}}}}\cap ...\cap {{P}_{{{i}_{h}}}}|$表示极大项相交集中极大项的个数,称形如${{P}_{{{i}_{1}}}}\cap {{P}_{{{i}_{2}}}}\cap ...\cap {{P}_{{{i}_{h}}}}\cap {{P}_{k}}$的公式为其扩展极大项相交集.用ET(Q)表示极大项相交集Q的所有扩展极大项相交集;相应地,称子句集{Ci1,Ci2,…,Cih}为${{P}_{{{i}_{1}}}}\cap {{P}_{{{i}_{2}}}}\cap ...\cap {{P}_{{{i}_{h}}}}$的基础子句集,并用 BS(Q)表示极大项相交集Q的基础子句集.其中,h=1,2,…,n,k≠i1,i2,…,ih且i1<i2<…<ih<k.特殊地,称h=1时的极大项相交集为单相交集.
由定义8可知:一个极大项相交集的基础子句集是其扩展极大项相交集基础子句集的子集,且只相差一个子句元素.基于它们之间这种扩展关系,下面给出已知前者的互补性判断后者是否广义互补的定理.
定理7. 给定极大项相交集Q和Q',且Q'$ \in $ET(Q),BS(Q')=BS(Q)$\cup ${C}:
1) 若已知基础子句集BS(Q)广义互补,那么BS(Q')也广义互补;
2) 若已知基础子句集BS(Q)不是广义互补的,那么BS(Q')是广义互补当且仅当BS(Q)中至少存在一个子句与C互补.
证明:
1) 由定义6可知:若BS(Q)是广义互补的,那么它至少包含一对互补子句;又因为BS(Q)是BS(Q')的子集,所以BS(Q')中也含有互补子句对,故BS(Q')也是广义互补的;
2) 当BS(Q)不是广义互补的,即,BS(Q)中不含有互补子句对时:
 充分性:若BS(Q')是广义互补的,在BS(Q)$\cup ${C}中必有互补子句对;又由于BS(Q)中子句两两之间不互补,故其中必然至少存在一个子句与C互补;
充分性:若BS(Q')是广义互补的,在BS(Q)$\cup ${C}中必有互补子句对;又由于BS(Q)中子句两两之间不互补,故其中必然至少存在一个子句与C互补;
 必要性:反之,当BS(Q)中至少存在一个子句与子句C互补时,显然,子句集BS(Q')是广义互补的.
必要性:反之,当BS(Q)中至少存在一个子句与子句C互补时,显然,子句集BS(Q')是广义互补的.
下面给出已知极大项相交集的值,计算其扩展极大项相交集的定理:
定理8. 对于给定的极大项相交集Pi$\cap $Pj$\cap $…$\cap $Pl和它的一个扩展极大项相交集Pi$\cap $Pj$\cap $…$\cap $Pl$\cap $Pk:
1) 若子句集{Ci,Cj,…,Cl,Ck}是广义互补的,则有|Pi$\cap $Pj$\cap $…$\cap $Pl$\cap $Pk|=0;
2) 若子句集{Ci,Cj,…,Cl,Ck}不是广义互补的,则有|Pi$\cap $Pj$\cap $…$\cap $Pl$\cap $Pk|=|Pi$\cap $Pj$\cap $…$\cap $Pl|/2|Z|,其中,Z={x|x$ \in $ Ck且x$\notin $Ch,h=i,j,…,l}.
证明:
1) 若子句集{Ci,Cj,…,Cl,Ck}为广义互补时,由定理6可知,|Pi$\cap $Pj$\cap $…$\cap $Pl$\cap $Pk|=0;
2) 若子句集{Ci,Cj,…,Cl,Ck}不是广义互补的,显然,子句集{Ci,Cj,…,Cl}也不是广义互补的,则有$|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{l}}|=\mathop{2}^{|X|-|{{C}_{i}}\cup {{C}_{j}}\cup ...\cup {{C}_{l}}|}$,而且$|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{l}}\cap {{P}_{k}}|=\mathop{2}^{|X|-|{{C}_{i}}\cup {{C}_{j}}\cup ...\cup {{C}_{l}}\cup {{C}_{k}}|}$,由此可得如下公式:
$|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{l}}\cap {{P}_{k}}|=|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{l}}|/\mathop{2}^{|{{C}_{i}}\cup {{C}_{j}}\cup ...\cup {{C}_{l}}\cup {{C}_{k}}|-|{{C}_{i}}\cup {{C}_{j}}\cup ...\cup {{C}_{l}}|}$
其中,|Ci$\cup $Cj$\cup $…$\cup $Cl$\cup $Ck|-|Ci$\cup $Cj$\cup $…$\cup $Cl|即表示包含在子句Ck中同时不被子句Ci,Cj,…,Cl包含的文字个数,即|Z|.
例5:对于一个包含子句C1,C2的子句集$\Phi $,计算其所能扩展出的极大项个数时,假设C1,C2不互补,已知$|{{P}_{1}}|={{2}^{|X|-|{{C}_{1}}|}}$,所以计算|P1|时只需要遍历子句C1,计算其长度即可.而在计算|P1$\cap $P2|时要计算出|C1$\cup $C2|,即,要遍历C1和C2计算它们总共包含多少个文字.而P1$\cap $P2是P1的扩展极大项相交集,根据定理8,计算|P1$\cap $P2|恰恰可以利用计算|P1|时的结果,只计算C2与C1不同的文字数即可.
CER方法在利用公式(1)分层求解给定子句集所能扩展出的极大项个数时,未能考虑极大项相交集和扩展极大项相交集之间的扩展关系.为在计算扩展极大项相交集时能充分利用对应的极大项相交集计算后的结果,对CER方法中的公式(1)进行重构,其重构后的公式如下:
$S=\sum\limits_{i=1}^{n}{\left( |{{P}_{i}}|-\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{i}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \right)}$
(2)
定理9. 公式(2)与公式(1)等价.
证明:
$\begin{align}
& S=\sum\limits_{i=1}^{n}{\left( |{{P}_{i}}|-\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap \cap ...{{P}_{n}}|)...)} \right)} \right)} \\
& ~~~~=\sum\limits_{i=1}^{n}{|{{P}_{i}}|}-\sum\limits_{i=1}^{n}{\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap \cap ...{{P}_{n}}|)...)} \right)}} \\
& ~~~~=\sum\limits_{i=1}^{n}{|{{P}_{i}}|}-\sum\limits_{1\le i<j\le n}{|{{P}_{i}}\cap {{P}_{j}}|}+\sum\limits_{i=1}^{n}{\sum\limits_{j=i+1}^{n}{\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap \cap ...{{P}_{n}}|)...)}}} \\
& \text{ }... \\
& ~~~~=\sum\limits_{i=1}^{n}{|{{P}_{i}}|}-\sum\limits_{1\le i<j\le n}{|{{P}_{i}}\cap {{P}_{j}}|}+\sum\limits_{1\le i<j<l\le n}{|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|}-...+{{(-1)}^{n-1}}|{{P}_{i}}\cap {{P}_{j}}\cap \cap ...{{P}_{n}}|. \\
\end{align}$
由以上推导过程可知,公式(1)与公式(2)是等价的.
公式(2)是公式(1)等价的重构表达形式,下面给出公式(2)的展开过程:
$\begin{align}
& S=\sum\limits_{i=1}^{n}{\left( |{{P}_{i}}|-\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \right)} \\
& ~~~~=|{{P}_{1}}|-\sum\limits_{j=2}^{n}{\left( |{{P}_{1}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{1}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{1}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \\
& ~~~~~~~+\sum\limits_{i=2}^{n}{\left( |{{P}_{i}}|-\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \right)}~~ \\
& ~~=|{{P}_{1}}|-|{{P}_{1}}\cap {{P}_{2}}|+\sum\limits_{l=3}^{n}{(|{{P}_{1}}\cap {{P}_{2}}\cap {{P}_{l}}|-...-(|{{P}_{1}}\cap {{P}_{2}}\cap ...\cap {{P}_{n}}|)...)} \\
& \text{ }-\sum\limits_{j=3}^{n}{\left( |{{P}_{1}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{1}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{1}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \\
& ~+\sum\limits_{i=2}^{n}{\left( |{{P}_{i}}|-\sum\limits_{j=i+1}^{n}{\left( |{{P}_{i}}\cap {{P}_{j}}|-\sum\limits_{l=j+1}^{n}{(|{{P}_{i}}\cap {{P}_{j}}\cap {{P}_{l}}|-...-(|{{P}_{i}}\cap {{P}_{j}}\cap ...\cap {{P}_{n}}|)...)} \right)} \right)} \\
& \text{ }... \\
\end{align}$
RCER方法按照公式(2)以上展开形式顺序计算极大项相交集和其扩展极大项相交集的值,下面给出结合公式(2)对极大项相交集对应的扩展极大项相交集进行剪枝的相关推论.
由定义6和定理6易得如下推论:
推论1. 已知一个广义互补的子句集$\Phi $,则子句集$\Phi $的任意超集$\Phi $'中所有子句扩展出的极大项集合交集必为空.
证明:由定义6可知,子句集$\Phi $中必有互补子句对,所以包含这个子句集的任意子句集$\Phi $'也必然含有互补子句对,是广义互补的;再根据定理6可知,子句集$\Phi $'中所有子句扩展出的极大项集合交集必为空. □
例6:给定一个子句集$\Phi $={C1,C2,C3,C4},若子句C1和C2互补,那么不仅|P1$\cap $P2|=0,只要以同时包含C1,C2的子句集为基础子句集的极大项相交集,其值也必为0,如,{C1,C2,C3},{C1,C2,C4},{C1,C2,C3,C4}对应的极大项相交集P1$\cap $P2$\cap $P3,P1$\cap $P2$\cap $P4,P1$\cap $P2$\cap $P3$\cap $P4,的值都等于0.
由推论1可知:在公式(2)的计算过程中,已知一个极大项相交集的值为0,便可得其所有扩展极大项相交集的值也为0,从而可将其对应的冗余计算项提前从公式(2)中删除,减少不必要的计算.
下面给出求解扩展极大项相交集时,充分利用极大项相交集计算结果的增量求解方法.
3.2 极大项相交集增量计算方法事实上,公式(2)中所有极大项相交集的基础子句集是需求解子句集幂集中的元素,只要对相应的基础子句集中子句进行文字计数,便可求出该极大项相交集的值.按照公式(2)展开形式的计算顺序,一般情况下,下一个即将计算的极大项相交集是上一个已计算的极大项相交集的扩展极大项相交集,可在上一个已计算的极大项相交集结果的基础上增量计算,即,只需对每次求解时多出的一个子句进行文字计数,避免了对子句集中所有子句逐一遍历求解.
按照公式(2)展开形式进行极大项个数求解,充分利用了极大项相交集和扩展极大项相交集之间的扩展关系:(a) 根据定理7,判断当前极大项相交集Q'的基础子句集BS(Q')是否广义互补时,BS(Q')除了包含之前已计算极大项相交集Q的基础子句集BS(Q)中所有子句外,还包含一个不在BS(Q)中的子句,只需要判断此子句是否与BS(Q)中的子句互补即可.因BS(Q)中子句对的互补情况已经判断过,无需重复计算;(b) 根据定理8,在计算当前极大项相交集Q'的值时,上一个已计算的极大项相交集Q的基础子句集比Q'的基础子句集少包含一个子句,只需要计算此子句中没有被BS(Q)覆盖的文字个数即可.
下面给出基于扩展规则重构的#SAT增量求解方法RCER.
算法. RCER ($\Phi $={C1,C2…,Cn},X={x1,x2,…,xm}).
01. 初始化:BS=∅,inte_V=0,Prev_com=0,Sum=0,Prev_VarCover$m$={0};
02. Count_Max_terms(BS,inte_V,Prev_com,Prev_VarCover)
03. BEGIN
04. For (i=inte_V; i<n; i++)
05. IF (BS$\cup ${Ci}中有互补子句对) THEN
06. Continue;
07. ENDIF
08. Fol_VarCover$m$←Prev_VarCover$m$;
09. Fol_com←Prev_com;
10. For (Ci中每个变量xj)
11. IF (Fol_VarCover$j$==0) THEN
12. Fol_VarCover$j$=1;
13. Fol_com++;
14. ENDIF
15. ENDFor
16. IF (BS$\cup ${Ci}共包含奇数个子句) THEN
17. Sum+=2m-Fol_com;
18. ELSE
19. Sum-=2m-Fol_com;
20. ENDIF
21. Count_Max_terms(BS$\cup ${Ci},i+1,Fol_com,Fol_VarCover);
22. ENDFor
23. END
24. Num_models=2m-Sum;
25. Return Num_models;
算法中,BS代表极大项相交集的基础子句集,即,子句集$\Phi $的子集,初始时为∅.用Sum表示子句集$\Phi $能扩展出的极大项个数,Prev_com表示前一个基础子句集中变量个数,并且用数组Prev_VarCover$m$记录都有哪些变量:若有变量xi,则Prev_VarCover$i$的值为1;否则为0.而Fol_com则表示当前的基础子句集中变量个数,对应的Fol_VarCover$m$则记录当前基础子句集的变量覆盖情况.Count_Max_terms是求解Sum值的递归函数,每调用一次函数就进入下一层的计算,即,开始计算当前极大项相交集的扩展极大项相交集.若当前要计算极大项相交集的基础子句集是广义互补的,那么直接进行下一次循环.通过这种方式,较好地避免了对其值必为0的极大项相交集的冗余计算.
RCER算法的主要工作是计算给定子句集所能扩展出的极大项个数,根据公式(2)的展开形式计算可以充分利用计算项之间的扩展关系,不仅在上一次计算结果上进行增量计算,还可避免多数冗余项的计算,进而较好地提高了计算效率.在RCER算法中,每生成一个极大项相交集的基础子句集,都要判断其中是否含有互补子句对,若每次都对相应基础子句集中的所有子句对进行遍历判断是否含有互补文字,则降低了判断效率.因此,提出一种基于互补表的增量判定方法来提高效率.
3.3 互补表增量判定方法该方法中构建一个互补表,对子句间的互补关系进行记录.考虑到空间复杂性,互补表由一个下三角矩阵构成.互补表中对角线位置记录相应子句与其他子句互补情况,互补表中其他位置记录相应子句对的互补关系.互补表方法有效避免了互补判定中的重复计算,尤其是相应子句与其他所有子句都不互补时可直接得到判定结果.包含4个子句的子句集$\Phi $={C1,C2,C3,C4}的互补表如图2所示.

|
图2 互补表示例 Fig.2 Example of complementary table |
若子句Ci与子句Cj是互补的,则表中元素ai,j=1;否则,ai,j=0.通过这种方式,互补表可以记录所有子句间的互补关系.当多次判断同一子句对是否互补时,除第1次判断外,仅需要查找互补表中相应元素的值即可.表中ai,i的值等于第i行中除其之外所有元素的和,即,ai,i表示子句Ci与C1,…,Ci-1中互补的子句个数.初始时,可将表中除对角线外所有的元素设为较大的值,如n(给定子句集中子句个数),且ai,i初始值为(i-1)n.
在RCER方法中,根据定理7,可以在极大项相交集的基础上增量计算扩展极大项相交集基础子句集是否广义互补,进而提高子句集广义互补的判定效率.当前需判定的极大项相交集基础子句集是前一个已判断的极大项相交集基础子句集的超集,且只多包含一个子句,只需判断这个子句与基础子句集中其他子句是否互补即可.根据RCER算法中极大项相交集基础子句集生成顺序,新生成的基础子句集中多包含的子句在当前子句集中标号最大,这里用Cl表示,按照如下步骤判断基础子句集是否广义互补:
1) 在互补表中,先查找对角线元素al,l的值是否为0,即,是否与标号小于它的其他所有子句都不互补.如果都不互补,则直接得知此基础子句集不是广义互补子句集;
2) 若l-al,l的值小于当前子句集中子句个数,即C1,C2,…,Cl-1中与Cl不互补的子句个数小于当前子句集中除Cl外的子句个数,则子句集中必然存在与Cl互补的子句,故基础子句集是广义互补的;
3) 否则,继续在表中分别查找相应位置,判断子句Cl与基础子句集中其他子句是否互补.
互补表增量判定方法较大程度地减少CER算法在判断互补时所花费的时间,提高了算法效率.下面给出判断子句集中是否含有互补子句对的增量判定方法.
EST_Complementry($\Phi $).
/*$\Phi $为当前基础子句集,假设$\Phi $中Cl为标号最大子句,且$\Phi $中子句个数为k*/
01. IF al,l==0 THEN Return False;
02. IF l-k<al,l<l THEN Return True;
03. For ($\Phi $中除Cl外的其他每个子句Ci)
04. IF al,i==1 THEN Return True;
05. IF al,i==n THEN
06. 遍历Cl,Ci;
07. IF Cl与Ci含互补文字 THEN
08. al,i=1;
09. al,l=al,l-(n-1);
10. Return True;
11. ELSE
12. al,i=0;
13. al,l=al,l-n;
14. ENDIF
15. ENDIF
16. ENDFOR
17. Return False;
4. 实验结果本节将RCER方法与CER方法进行比较,并给出两种方法在随机问题实验测试用例的结果.实验平台如下: Windows XP操作系统,CPU AMD Athlon(tm) 64 X2 Dual Core Processor 3600+ 1.9GHz,2.00GB RAM.
实验用例由随机生成器产生,其输入参数有变量个数m、子句个数n以及变量在每个子句中的出现概率p,每个子句都按一定概率p从m个变量中选取变量,因变量的正负文字相对于子句集来说是对称的,所以这里只控制变量为正的概率p',p'范围是(0.1,0.5).本文的实验数据采用变量个数为30,子句个数为100的随机样例进行实验测试.通过限定变量在子句中出现的概率,并结合其正文字出现的概率来限定子句集中子句的平均子句长度以及互补因子的大小.实验测试互补因子范围为(0.1~0.9),实验结果是10次实验的平均结果.
从图3的对比图中可以看到:在大部分测试用例中,RCER方法的求解效率要比CER方法有明显提高,并且图中有些散点已经达到2倍对比线甚至3倍对比线.但是注意到:在耗时相对较少的例子中,效率提高并不明显,甚至对于一些测试用例两种方法求解时间相近.

|
图3 RCER方法与CER方法实验结果比较 Fig.3 Experimental comparisons of RCER and CER |
RCER方法与CER方法的效率受互补因子影响较大,当互补因子较高时,公式(1)和公式(2)中存在较多的计算项值为0,需要计算的项就相对较少,从而两种方法的效率就越高.为了更好地测试这两种方法的性能与互补因子的关系,下面给出互补因子由低到高变化时,两种方法对应实验的对比结果,如图4所示.
从图4可以看出:
· 随着互补因子的提高,RCER方法与CER方法的求解时间都急速下降;并且在互补因子较低时,RCER方法求解效率明显高于CER方法;
· 随着互补因子的增大,两方法的求解时间差逐渐缩小;且当互补因子大于0.6时,两个方法的求解时间差开始明显缩小;
· 互补因子更大时,RCER方法的求解时间还要略高于CER方法.
当互补因子较高时,子句集中互补的子句对相对就较多,从而公式(1)和公式(2)中值为0的计算项就较多,需要计算的项就较少.这样,在RCER方法中可以利用的极大项相交集之间的扩展关系较少,所以此时两种方法的求解时间相差不大.由于需要对当前子句集中的文字覆盖情况进行记录,所以有时效率会略低于CER方法.值得注意的是:虽然互补因子较高时,相对于CER方法,RCER方法并没有显著提高,但是在这种情况下,CER方法的求解时间已经很少,算法效率的提升空间已经很小;并且在这种情况下,RCER方法的求解效率也依然较高.
从图4(a)中容易发现:对于互补因子较低的测试用例,算法的求解时间相对并不是很多.原因在于:算法实现中加入了单元子句规则,这里用变量在子句中出现的概率和其正负文字出现的概率来控制互补因子大小,因此,当一个子句集互补因子较小时,其中可能包含较多的单元子句,再通过单元子句规则对子句集进行处理,就可以减少子句集规模,从而使得求解时间减少.

|
图4 不同互补因子下两种方法实验结果比较 Fig.4 Experimental comparisons of the two methods based on diverse complementary factors |
下面给出两个算法对图4中各测试用例的求解时间比,见表1.
| 表1 时间比(s/s) Table 1 Time ratio (s/s) |
从表1可以看出:CER方法求解时间与RCER方法求解时间的比值随着互补因子的增大在逐渐减小,并在互补因子0.6之后减小趋势更加明显.即:随着互补因子的增大,RCER方法比CER方法的效率提升越来越不明显.可以想象:在极端情况下,当子句集互补因子为1时,即,子句集中任意两个子句都是互补的情况,公式(1)和公式(2)中需要计算的项仅有n个单相交集组成的计算项,此时的计算项间都不存在扩展关系,所以RCER方法与CER方法的计算过程是一样的.然而,RCER方法还需对每个项中文字覆盖情况进行记录,因此,CER方法的效率要高于RCER方法.虽然这种情况非常少,但可以依据这种趋势来理解随着互补因子的增大,RCER方法的优势逐渐减小的原因.
5. 结束语#SAT问题计算CNF公式的模型个数,是SAT问题的一种扩展问题,在人工智能领域具有广泛应用,如可以在多项式时间内与贝叶斯推理问题进行转化.在对扩展规则在SAT及#SAT求解问题中的应用进行深入研究和分析后,对已有的基于扩展规则的模型计数求解方法CER进行改进.CER方法在求解时没有充分利用极大项相交集和其扩展极大项相交集之间的扩展关系来避免冗余计算.针对此问题,本文给出适合增量求解的RCER方法.此方法优先计算扩展极大项相交集对应极大项个数,并重用极大项相交集计算结果;对广义互补子句集对应的所有扩展极大项相交集进行剪枝,有效避免了计算所有极大项相交集对应极大项个数时的冗余求解;优先判定扩展极大项相交集互补关系,并重用极大项相交集互补结果的互补判定增量方法,较好地避免了判断子句间和各极大项相交集的基础子句集互补关系时的重复计算.实验结果表明:两种方法在互补因子较高的问题中具有较快的求解速度;并且在互补因子较低的问题中,RCER算法的求解效率明显优于CER算法,效率提升2~3倍.
致谢 本文作者对所有的匿名审稿人的辛勤工作和给予本文宝贵的意见表示真诚的感谢.
| [1] | Monasson R, Zecchina R, Kirkpatrick S, Selman B, Troyansky L. Determining computational complexity from characteristic 'phase transitions'. Nature, 1999,400(6740):133-137.[doi:10.1038/22055] |
| [2] | Mezard M, Parisi G, Zecchina R. Analytic and algorithmic solution of random satisfiability problems. Science, 2002,297(5582):812-815.[doi:10.1126/science.1073287] |
| [3] | Zhang LT, Madigan CF, Moskewicz MH, Malik S. Efficient conflict driven learning in a Boolean satisfiability solver. In:Pileggi LT, Kuehlmann A, eds. Proc. of the 2001 IEEE/ACM Int'l Conf. on Computer-Aided Design(ICCAD 2001). Piscataway:IEEE Press, 2001. 279-285.[doi:10.1109/ICCAD.2001.968634] |
| [4] | Pan XY, Jiao LC, Liu F. A multi-agent social evolutionary algorithm for SAT problem. Chinese Journal of Computers, 2014,37(9):2011-2020(in Chinese with English abstract). |
| [5] | Kautz H, Selman B. Planning as satisfiability. In:Neumann B, ed. Proc. of the 10th European Conf. on Artificial Intelligence(ECAI'92). Vienna:John Wiley and Sons, 1992. 359-363. |
| [6] | Kautz H, Selman B. Unifying SAT-based and graph-based planning. In:Dean T, ed. Proc. of the 16th Int'l Joint Conf. on Artificial Intelligence(IJCAI'99). Stockholm:Morgan Kaufmann Publishers, 1999. 318-325. |
| [7] | Kautz H. Deconstructing planning as satisfiability. In:Veloso M, Kambhampati S, eds. Proc. of the 21st National Conf. on Artificial Intelligence(AAAI 2006). Menlo Park:AAAI Press, 2006. 1524-1526. |
| [8] | Grastien A, Anbulagan A. Diagnosis of discrete event systems using satisfiability algorithms:A theoretical and empirical study. IEEE Trans. on Automatic Control, 2013,58(12):3070-3083.[doi:10.1109/TAC.2013.2275892] |
| [9] | Cook SA. The complexity of theorem-proving procedures. In:Harrison MA, Banerji RB, Ullman JD, eds. Proc. of the 3rd Annual ACM Symp. on Theory of Computing. New York:ACM Press, 1971. 151-158.[doi:10.1145/800157.805047] |
| [10] | Valiant LG. The complexity of computing the permanent. Theoretical Computer Science, 1979,8(2):189-201.[doi:10.1016/0304- 3975(79)90044-6] |
| [11] | Roth D. On the hardness of approximate reasoning. Artificial Intelligence, 1996,82(1):273-302.[doi:10.1016/0004-3702(94) 00092-1] |
| [12] | Majercik SM, Littman ML. Contingent planning under uncertainty via stochastic satisfiability. Artificial Intelligence, 2003, 147(1-2):119-162.[doi:10.1016/S0004-3702(02)00379-X] |
| [13] | Dubois O. Counting the number of solutions for instances of satisfiability. Theoretical Computer Science, 1991,81(1):49-64.[doi:10.1016/0304-3975(91)90315-S] |
| [14] | Zhang WH. Number of models and satisfiability of sets of clauses. Theoretical Computer Science, 1996,155(1):277-288.[doi:10.1016/0304-3975(95)00144-1] |
| [15] | Birnbaum E, Lozinskii EL. The good old Davis-Putnam procedure helps counting models. Journal of Artificial Intelligence Research, 1999,10(1):457-477.[doi:10.1613/jair.601] |
| [16] | Bayardo RJ, Pehoushek JD. Counting models using connected components. In:Kautz H, Porter B, eds. Proc. of the 17th National Conf. on Artificial Intelligence(AAAI 2000). Menlo Park:AAAI Press, 2000. 157-162. |
| [17] | Sang T, Bacchus F, Beame P, Kautz H, Pitassi T. Combining component caching and clause learning for effective model counting. In:Hans KB, Zhao XS, eds. Proc. of the SAT 2004. Berlin, Heidelberg:Spinger-Verlag, 2004. 20-28. |
| [18] | Sang T, Beame P, Kautz H. Heuristics for fast exact model counting. In:Bacchus F, Walsh T, eds. Proc. of the SAT 2005. Berlin, Heidelberg:Springer-Verlag, 2005. 226-240.[doi:10.1007/11499107_17] |
| [19] | Thurley M. SharpSAT-Counting models with advanced component caching and implicit BCP. In:Biere A, Gomes CP, eds. Proc. of the SAT 2006. Berlin, Heidelberg:Springer-Verlag, 2006. 424-429.[doi:10.1007/11814948_38] |
| [20] | Lin H, Sun JG, Zhang YM. Theorem proving based on the extension rule. Journal of Automated Reasoning, 2003,31(1):11-21.[doi:10.1023/A:1027339205632] |
| [21] | Wu X, Sun JG, Lin H, Feng SS. Modal extension rule. Progress in Natural Science, 2005,15(6):550-558.[doi:10.1080/10020070512331342540] |
| [22] | Lai Y, Ouyang DT, Cai DB, Lü S. Model counting and planning using extension rule model counting and planning using extension rule. Journal of Computer Research and Development, 2009,46(3):459-469(in Chinese with English abstract). |
| [23] | Lin H, Sun JG. Knowledge compilation using the extension rule. Journal of Automated Reasoning, 2004,32(2):93-102.[doi:10.1023/B:JARS.0000029959.45572.44] |
| [24] | Sun JG, Li Y, Zhu XJ, Lü S. A novel theorem proving algorithm based on extension rule. Journal of Computer Research and Development, 2009,46(1):9-14(in Chinese with English abstract). |
| [25] | Zhang LM, Ouyang DT, Bai HT. Theorem proving algorithm based on semi-extension rule. Journal of Computer Research and Development, 2010,47(9):1522-1529(in Chinese with English abstract). |
| [26] | Li Y, Sun JG, Wu X, Zhu XJ. Extension rule algorithms based on IMOM and IBOHM heuristics strategies. Ruan Jian Xue Bao/Journal of Software, 2009,20(6):1521-1527(in Chinese with English abstract).http://www.jos.org.cn/1000-9825/3420.htm[doi:10.3724/SP.J.1001.2009.03420] |
| [27] | Yin MH, Lin H, Sun JG. Solving #SAT using extension rules. Ruan Jian Xue Bao/Journal of Software, 2009,20(7):1714-1725(in Chinese with English abstract).http://www.jos.org.cn/1000-9825/3320.htm[doi:10.3724/SP.J.1001.2009.03320] |
| [28] | Biere A, Heule M, van Maaren H, Walsh T. Handbook of Satisfiability. Amsterdam:IOS Press, 2009,3-4:633-634. |
| [29] | Sun JG, Yang FJ, Ouyang DT, Li ZS. Discrete Math. Beijing:Higher Education Press, 2002. 4-5(in Chinese). |
| [30] | 潘晓英,焦李成,刘芳.求解SAT问题的多智能体社会进化算法.计算机学报,2014,37(9):2011-2020.[doi:10.3724/SP.J.1016.2014. 02011] |
| [31] | 赖永,欧阳丹彤,蔡敦波,吕帅.基于扩展规则的模型计数与智能规划方法.计算机研究与发展,2009,46(3):459-469. |
| [32] | 孙吉贵,李莹,朱兴军,吕帅.一种新的基于扩展规则的定理证明算法.计算机研究与发展,2009,46(1):9-14. |
| [33] | 张立明,欧阳丹彤,白洪涛.基于半扩展规则的定理证明方法.计算机研究与发展,2010,47(9):1522-1529. |
| [34] | 李莹,孙吉贵,吴瑕,朱兴军.基于IMOM和IBOHM启发式策略的扩展规则算法.软件学报,2009,20(6):1521-1527.http://www.jos.org.cn/1000-9825/3420.htm[doi:10.3724/SP.J.1001.2009.03420] |
| [35] | 殷明浩,林海,孙吉贵.一种基于扩展规则的#SAT求解系统.软件学报,2009,20(7):1714-1725.http://www.jos.org.cn/1000-9825/3320.htm[doi:10.3724/SP.J.1001.2009.03320] |
| [36] | 孙吉贵,杨凤杰,欧阳丹彤,李占山.离散数学.北京:高等教育出版社,2002.4-5. |
 2015, Vol. 26
2015, Vol. 26


