德国数学家Wille教授于1982年提出了形式概念的理论[1].设U是对象集合,M是属性集合,I⊆UxM是U 与M间的关系,则称三元组K=(U,M,I)为一个形式背景.若A⊆U,B⊆M,令f(A)={m$\in $M|∀u$\in $A:(u,m)$\in $I},g(B)={u$\in $U| ∀m$\in $B:(u,m)$\in $I},并认为若f(A)=B,g(B)=A,则(A,B)是一个形式概念.A是这个概念的外延,B是这个概念的内涵.K的全部概念的集合记作B(K).若B(K),且A1⊆A2(可以证明,此时必有B2⊆B1)则称(A1,B1)是(A2,B2)的子概念,(A2,B2)是(A1,B1)的父概念,并且记作(A1,B1)≤(A2,B2).已证明[1]集合B(K)以≤为偏序是一个格(请见本文第1节形式概念的基础定理).因此,形式概念的理论又称为概念格理论.若A1是A2的真子集,则记(A1,B1)<(A2,B2).若(A1,B1)<(A2,B2),且不存在概念(A3,B3)使(A1,B1)<(A3,B3)<(A2,B2),则称(A1,B1)是(A2,B2)的直接子概念,(A2,B2)是(A1,B1)的直接父概念,记作(A1,B1)p(A2,B2).有向图(S,L)称为是概念格B(K)的Hasse图,其中,B(K)是点的集合,L是有向边的集合,当且仅当(A1,B1)f(A2,B2)时,((A1,B1),(A2,B2))$\in $L.且在绘制时,要求父概念总在子概念上面,并由此而略去有向边的箭头.由一个形式背景求出它的全部概念及这些概念形成的Hasse图,称为概念格的构造.
现在,形式概念已得到了广泛的应用,例如在软件工程[2]、地理信息系统[3]、入侵检测[4]、Web日志挖掘[5]、客户群聚类[6]、Apsect挖掘[7]、动态知识学习[8]、空间聚类[9]、病症智能诊断[10]、Folksonomy[11]、访问控制权限管理[12]、软件演化分析[13]、二值命题逻辑约简[14]等很多领域都有了成功的应用.然而,概念的个数是随背景的尺寸指数级增长的,因此,概念格的构造一直是很受关注的课题.目前,构造概念格的方法可分为两种:批处理算法[15]及渐进式算法[16, 17, 18, 19].
直到2013年,渐进式构造算法都是背景增加属性或增加对象时的渐增式构造算法.然而实际应用中,有时背景的变化并不是增加属性(或对象),而是减少属性(或对象),例如在Web信息检索的背景中,对象是Web文档,属性是关键词.随着时间的推移,有些关键词不再被人们所关注了,若继续将它们保存在背景中,长期积累下来将会使概念格越来越大,无效的概念越来越多,信息检索的速度越来越下降.因此,应该将不再受关注的关键词从背景中删除,压缩概念格的规模,提高检索速度.
2013年,张磊等人[20]研究了当形式概念的某些属性削减之后,如何快速有效地在原有的概念格上进行调整,得到新形式背景的概念格,而不是传统方式下的重新构造的算法.张磊等人给出了减少一个属性时自底向上与自顶向下的渐减式算法,能够同时对概念格及Hasse图进行调整,而且有良好的时间性能,在这个方向上做了开创性的工作.但该算法每次只能减少一个属性,而实际问题中只减少一个属性的情况是较少的,一般是要减少一些属性,例如要删除与某个问题相关的一组关键词.这时,减少一个属性的算法必须反复执行多次.能否将每次减少一个属性的算法推广为每次减少多个属性的算法呢?研究发现:每次减少一个属性的算法不能简单地推广为每次减少多个属性的算法,因为减少一个属性时的许多性质在减少多个属性时不再成立.例如,一个删除基只对应一个删除节点,删除节点必然在某个保留节点与某个更新节点之间,…,等等,在减少多个属性时都不再成立.因此,一次减少多个属性时必须研究新方法.张磊等人在文献[20]中指出研究同时删除一个以上属性的概念格的属性渐减算法,无疑也是一件很有意义的事情.本文将解决这个问题,给出一次减少多个属性时快速有效地在原有概念格的基础上得到新背景的概念格的方法.
本文第1节给出形式概念的基础定理.第2节给出多属性减少的基本原理.第3节介绍多属性减少的算法.第4节是验证.第5节是后记.
1. 形式概念的基础定理定理1[1]. 设K=(U,M,I)为一个形式背景.若A,A1,A2⊆U,B,B1,B2⊆M,则函数f,g有以下性质:
(1) A1⊆A2,则f(A1)⊇f(A2);
(2) B1⊆B2,则g(B1)⊇g(B2);
(3) f(A1$\cup $A2)=f(A1)$\cap $f(A2);
(4) g(B1$\cup $B2)=g(B1)$\cap $g(B2);
(5) A⊆g(f(A));
(6) B⊆f(g(B));
(7) f(A)=f(g(f(A)));
(8) g(B)=g(f(g(B))).
而且由性质(8)可知:对于M的任何子集B,(g(B),f(g(B)))一定是概念,g(B)一定是外延.特别是(g(M),M)一定是概念,称其为零元概念.
对于$D\subseteq $B(K),若$({{A}_{0}},{{B}_{0}})\in $B(K)满足$\forall (A,B)\in D:(A,B)\ge ({{A}_{0}},{{B}_{0}})$,则称(A0,B0)是D的一个下界;若(A0,B0)满足$\forall (A,B)\in D:(A,B)\le ({{A}_{0}},{{B}_{0}})$,则称(A0,B0)是D的一个上界.
定理2. D所有下界的集合有最大元素,称该元素为D的下确界,记作$\wedge $D,且$\wedge D=(\underset{(A,B)\in D}{\mathop{\cap }}\,A,f(\underset{(A,B)\in D}{\mathop{\cap }}\,A))$; D所有上界的集合有最小元素,称该元素为D的上确界,记作$\wedge $D,且$\vee D=(g(\underset{(A,B)\in D}{\mathop{\cap }}\,B),\underset{(A,B)\in D}{\mathop{\cap }}\,B)$.
证明:首先,对任何$(C,D)\in D$都有$C\supseteq \underset{(A,B)\in D}{\mathop{\cap }}\,A$,于是$(\underset{(A,B)\in D}{\mathop{\cap }}\,A,f(\underset{(A,B)\in D}{\mathop{\cap }}\,A))\le (C,D)$,即是D的下界之一.若(E,F)是D的任意一个下界,则对所有$(A,B)\in D$都有A⊇E,于是$E\subseteq \underset{(A,B)\in D}{\mathop{\cap }}\,A$.这样,对D的任意一个下界(E,F),我们都有$(E,F)\le (\underset{(A,B)\in D}{\mathop{\cap }}\,A,f(\underset{(A,B)\in D}{\mathop{\cap }}\,A))$,所以$(\underset{(A,B)\in D}{\mathop{\cap }}\,A,f(\underset{(A,B)\in D}{\mathop{\cap }}\,A))$是D的下确界.
对偶可证$(g(\underset{(A,B)\in D}{\mathop{\cap }}\,B),\underset{(A,B)\in D}{\mathop{\cap }}\,B)$是D的一个上确界.
定理3. 设N⊆M,称背景K1=(U,N,I$\cup $UxN)为K的子背景.若我们记对K1求的f及g为f1及g1,则容易看出:
对所有A⊆U,都有f1(A)=f(A)$\cap $N,以及对所有B⊆N,都有g1(B)=g(B).
2. 多属性减少的基本原理定义1. 设背景K=(U,M,I),N⊆M,则称B(K)上的关系RN={((A,B),(C,D))|B$\cap $N=D$\cap $N}为N决定的等价关系(RN是等价关系的证明简单,略),称RN在B(K)上划分的任意个等价类都为N决定的等价类.
按定义1,同一等价类中的概念内涵与N的交都是相同的.
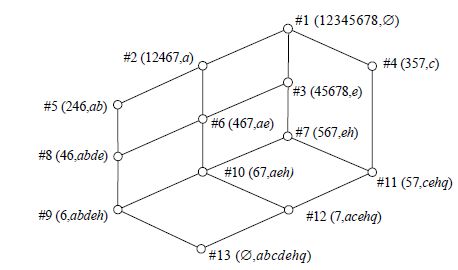
例1:设U={1,2,3,4,5,6,7,8},M={a,b,c,d,e,h,q},背景K=(U,M,I)见表1,概念格如图1所示,若N={a,c,q}, 则N决定的等价类如图2所示.其中,每一个闭曲线中的概念是一个等价类,同一个等价类中的概念的内涵与N交的共同值写在了该等价类闭曲线的旁边.具体如下:等价类{#1,#3,#7}中的概念的内涵与N的交都是空,等价类{#2,#5,#6,#8,#9,#10}中的概念的内涵与N的交都是a,等价类{#4}中的概念的内涵与N的交都是c,等价类{#11}中的概念的内涵与N的交都是cq,等价类{#12,#13}中的概念的内涵与N的交都是acq.
| 表1 一个形式背景 Table 1 A formal context |
|
图1 形式背景的概念格 Fig.1 Concept lattice of formal context |

|
图2 N决定的等价类 Fig.2 N determining equivalent classes |
我们将逐步证明:N决定的每个等价类都有最大元素,而最大元素与子背景中的概念一一对应.若原背景中有最大元素(A,B),则子背景中有概念(A,B$\cap $N).这个事实先请见例2.
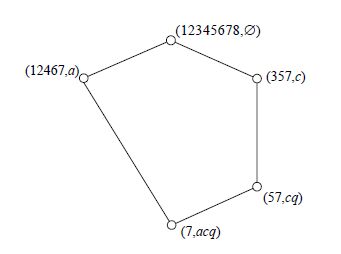
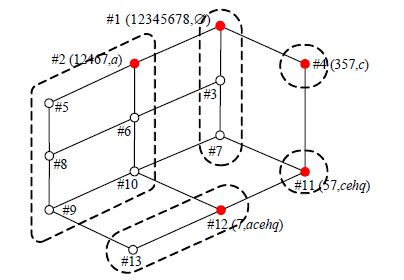
例2:对于例1中的K及N,子背景K1=(U,N,I$\cap $UxN)见表2,子背景的概念格如图3所示,原概念格中等价类的最大元素是#1,#2,#4,#11,#12概念,如图4中的实心圆所示.
其中,#1概念(12345678,∅)对应子背景中的(12345678,∅$\cap $N)=(12345678,∅),#2概念(12467,a)对应(12467,a$\cap $N)=(12467,a),#4概念(357,c)对应(357,c$\cap $N)=(357,c),#11概念(57,cehq)对应(57,cehq$\cap $N)=(57,cq),#12概念(7,acehq)对应(7,acehq$\cap $N)=(7,acq).
| 表2 一个子背景 Table 2 A subcontext |
|
图3 子背景的概念格 Fig.3 Concept lattice of subcontext |
|
图4 等价类的最大元素 Fig.4 Maxmal elements in equivalent classes |
下面逐步证明这个事实.
引理1. 设K=(U,M,I)是一个背景,N⊆M,w是N决定的一个等价类,则∨w$\in $w,且∨w是w的最大元素.
证明:设w={(At,Bt)|t$\in $T}(T是等价类w的索引集),于是,对∀t$\in $T,Bt$\cap $N都是相同的,令Bt$\cap $N=P.
由于$\vee \omega =\vee \{({{A}_{t}},{{B}_{t}})|t\in T\}=(g(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}),\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}})$,而对每一个t$\in $T都有Bt$\cap $N=P,所以,
$(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}})\cap N=\underset{t\in T}{\mathop{\cap }}\,({{B}_{t}}\cap N)=P.$
由于$(g(\underset{i\in {{T}_{0}}}{\mathop{\cap }}\,{{B}_{i}}),\underset{i\in {{T}_{0}}}{\mathop{\cap }}\,{{B}_{i}})$的内涵与N的交也为P,所以$(g(\underset{i\in {{T}_{0}}}{\mathop{\cap }}\,{{B}_{i}}),\underset{i\in {{T}_{0}}}{\mathop{\cap }}\,{{B}_{i}})\in \omega $.由于∨w是w的上界,所以∀t$\in $T都有 (At,Bt)≤∨w,所以,∨w是w的最大元素.
引理2. 设K=(U,M,I)是一个背景,N⊆M,$(A,B)\in $B(K),则:
f(g(B$\cap $N))$\cap $N=B$\cap $N.
证明:因B$\cap $N⊆f(g(B$\cap $N)),所以(B$\cap $N)$\cap $N⊆f(g(B$\cap $N))$\cap $N,即
B$\cap $N⊆f(g(B$\cap $N))$\cap $N
(1)
另外,B$\cap $N⊆B,f(g(B$\cap $N))⊆f(g(B)),而(A,B)是概念,所以f(g(B))=B,这样,f(g(B$\cap $N))⊆B.由此:
f(g(B$\cap $N))$\cap $N⊆B$\cap $N
(2)
由公式(1)、公式(2)知:
f(g(B$\cap $N))$\cap $N=B$\cap $N.
引理3. 设w={(At,Bt)|t$\in $T}是N决定的一个等价类,则对每个(At,Bt)$\in $w,都有:
∨w=(g(Bt$\cap $N),f(g(Bt$\cap $N)))).
证明:由于w是N决定的一个等价类,所以对于∀t$\in $T,Bt$\cap $N都是相同的,所以∀t$\in $T,(g(Bt$\cap $N),f(g(Bt$\cap $N))))都是相同的,设为(C,D).即,对∀t都有:
g(Bt$\cap $N))=C
(3)
f(g(Bt$\cap $N))=D
(4)
而且,由公式(4)及引理2还知:∀t,都有:
D$\cap $N=f(g(Bt$\cap $N))$\cap $N=Bt$\cap $N
(5)
所以(C,D)$\in $w.这样,D$\in ${Bt|t$\in $T}.于是:
$\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}\subseteq D$
(6)
并且另一方面,还由公式(5)得知:∀t,D$\cap $N⊆Bt.于是:
$D\cap N\subseteq \underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}$
(7)
然而,还由公式(5)及公式(3)得:
g(D$\cap $N)=g(Bt$\cap $N)=C=g(D)
(8)
这样,由公式(6)~公式(8),我们有:
$g(D\cap N)=g(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}})=g(D)=C$
(9)
因(C,D)及$(g(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}),\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}})$都是概念,所以:
$D=f(C)=f(g(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}))=\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}$
(10)
由公式(9)、公式(10)及公式(3)、公式(4)得:
$\begin{align}
& \vee \omega =\vee \{({{A}_{t}},{{B}_{t}})|t\in T\}=(g(\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}}),\underset{t\in T}{\mathop{\cap }}\,{{B}_{t}})=(C,D) \\
& =(g({{B}_{t}}\cap N),f(g({{B}_{t}}\cap N))). \\
\end{align}$
定理4. 设K=(U,M,I)是一个背景,N⊆M,K1=(U,N,I$\cup $UxN)是子背景,(A1,B1)是K1的概念,当且仅当存在N决定的某个等价类的最大元素(A,B)满足A1=A,B1=B$\cap $N.
证明:
(当):设(A,B)是N决定的某个等价类w的最大元素,令
A1=g1(B$\cap $N),B1=f1(g1(B$\cap $N)).
首先,由于B$\cap $N⊆N,所以(A1,B1)是K1的概念;其次,因为(A,B)是最大元素,由引理3中的公式(8)得知,g(B)=g(B$\cap $N);又因g(B)=A,所以A=g(B$\cap $N).因B$\cap $N⊆N,所以g(B$\cap $N)=g1(B$\cap $N)=A1,所以A=A1;最后,B1=f1(g1(B$\cap $N))=f1(g(B$\cap $N)),而f1(g(B$\cap $N))=f(g(B$\cap $N))$\cap $N,所以B1=f(g(B$\cap $N))$\cap $N.再由引理3中的公式(8)知g(B$\cap $N)=g(B),所以B1=f(g(B))$\cap $N,因(A,B)是概念,所以f(g(B))=B,所以B1=B$\cap $N.
(仅当):设(A1,B1)是K1的一个概念.令A=A1,B=f(A1).
首先,B$\cap $N=f(A1)$\cap $N=f1(A1)=B1;其次,我们证明(A,B)一定是K的一个概念,因为一方面B=f(A1)=f(A),另一方面A=A1=g(B1)=g(f(g(B1))).因B1⊆N,所以g(B1)=g1(B1)=A1.因此,A=g(f(g(B1)))=g(f(A1))=g(B),所以(A,B)是一个概念;最后,证明(A,B)一定是一个最大元素.因g(B$\cap $N)=g1(B$\cap $N)且B$\cap $N=f(A)$\cap $N=f(A1)$\cap $N=f1(A1)=B1,所以g(D$\cap $N)=g1(B$\cap $N)=g1(B1)=A1=A,f(g(B$\cap $N))=f(A)=B.所以(g(B$\cap $N),f(g(B$\cap $N)))=(A,B),由引理1及引理3得知,(A,B)是一个最大元素.
由定理4求出B(K)的所有最大元素(A,B),则所有(A,B$\cap $N)就是子背景K1的所有概念.我们称(A,B)与 (A,B$\cap $N)互为对应概念.
为了在原背景基础上得到子背景K1中概念的直接父子关系,做出子背景概念格的Hasse图,我们还有以下定理.
定理5. 若$({{C}_{1}},{{D}_{1}}),({{C}_{2}},{{D}_{2}})\in B\left( {{K}_{1}} \right)$,(C2,D2)f(C1,D1),(C1,D1),(C2,D2)在B(K)中对应的概念分别是(A1,B1)及 (A2,B2),则(A2,B2)是(A1,B1)某个直接父概念所在等价类的最大元素.
证明:因(A1,B1)及(A2,B2)分别是(C1,D1),(C2,D2)的对应概念,则A1=C1,A2=C2.由于(C2,D2)f(C1,D1),所以 C2⊃C1.于是,A2⊃A1.这样,(A2,B2)>(A1,B1),因此有(A1,B1)的直接父概念(A3,B3)满足(A2,B2)≥(A3,B3)>(A1,B1).于是B2⊆B3,B2$\cap $N⊆B3$\cap $N及g(B2$\cap $N)⊇g(B3$\cap $N).此时,或g(B2$\cap $N)=g(B3$\cap $N),或g(B2$\cap $N)⊃g(B3$\cap $N).
我们先证明g(B2$\cap $N)⊃g(B3$\cap $N)不可能,因为这将有(g(B2$\cap $N),f(g(B2$\cap $N)))>(g(B3$\cap $N),f(g(B3$\cap $N))),而(A2,B2)是(C2,D2)的对应概念,所以本身就是最大元素,所以由引理1及引理3得知(A2,B2)=(g(B2$\cap $N),f(g(B2$\cap $N))),于是(A2,B2)>(g(B3$\cap $N),f(g(B3$\cap $N))).再注意到(A3,B3)>(A1,B1),而(g(B3$\cap $N),f(g(B3$\cap $N)))是(A3,B3)所在等价类的最大元素,所以,
(g(B3$\cap $N),f(g(B3$\cap $N)))≥(A3,B3)>(A1,B1).
这样我们有:
(A2,B2)>(g(B3$\cap $N),f(g(B3$\cap $N)))≥(A1,B1),(A2,B2$\cap $N)>(g(B3$\cap $N),f(g(B3$\cap $N))$\cap $N)>(A1,B1$\cap $N),
即:
(C2,D2)>(g(B3$\cap $N),f(g(B3$\cap $N))$\cap $N)>(C1,D1).
因(g(B3$\cap $N),f(g(B3$\cap $N)))是最大元素,所以(g(B3$\cap $N),f(g(B3$\cap $N))$\cap $N)是子背景的概念,这与(C2,D2)是(C1,D1)的直接父概念矛盾,于是只能是g(B2$\cap $N)=g(B3$\cap $N).由此,显然有f(g(B2$\cap $N))$\cap $N=f(g(B3$\cap $N))$\cap $N.而由引理2得知,这时B2$\cap $N=B3$\cap $N,即(A2,B2)与(A3,B3)属于同一个等价类,于是,(A2,B2)就是(A1,B1)的直接父概念(A3,B3)所在等价类的最大元素.
3. 多属性减少的算法本文采用自底向上的算法,自顶向下的算法对偶可得.
我们用D存放子背景的概念,用L存放子背景的概念格Hasse图的边,用S存放待处理的那些最大元素.
子背景零元概念对应的概念显然是原背景的零元概念(g(M),M)所在等价类的最大元素.这个概念是
(g(M$\cap $N),f(g(M$\cap $N)))=(g(N),f(g(N))).
例如在例2中,子背景零元概念的对应概念是
(g(acq),f(g(acq)))=(7,acehq).
我们从原背景这个最大元素(g(N),f(g(N)))开始逐步向上处理.
若正在处理某个最大元素(A,B),则(A,B$\cap $N)就是子背景的一个概念,送入D,然后考察(A,B)的所有直接父概念(C,D).显然,(g(D$\cap $N),f(g(D$\cap $N)))是(C,D)所在等价类的最大元素.如果(g(D$\cap $N),f(g(D$\cap $N)))不曾在S中,则加到S尾.由于(g(D$\cap $N),f(g(D$\cap $N))$\cap $N)就是(g(D$\cap $N),f(g(D$\cap $N)))对应的子背景的概念,并且根据定理5得知,(A,B$\cap $N)的直接父概念就在由(A,B)的所有直接父概念(C,D)得出的(g(D$\cap $N),f(g(D$\cap $N))$\cap $N)这些概念中.例如在例2中,如果正在处理的最大元素(A,B)是#11概念(57,cehq),它对应的概念是子背景中的(57,cq),#11概念有两个直接父概念:#7概念(567,eh)及#4概念(357,c),而#7概念及#4概念所在等价类的最大元素分别是#1概念(12345678,∅)及#4概念(357,c),#1概念及#4概念对应的子背景的概念是(12345678,∅)及(357,c),于是,子背景的(57,cq)的直接父概念必在(12345678,∅)及(357,c)之中.
将(A,B)的所有直接父概念(C,D)得到的的这些(g(D$\cap $N),f(g(D$\cap $N))$\cap $N)送入临时变量P中,并进行“超集吸收”,即:在P中若有概念(I,J)的外延I是概念(E,F)的外延E的超集,则将(I,J)删掉.例如在例2中,将(12345678,∅)及(357,c)送入变量P中,并因(12345678,∅)的外延12345678是(357,c)的外延357的超集,于是在P中将(12345678, ∅)删掉.
显然,P中存放的将是(A,B$\cap $N)的全部直接父概念.将P中的每个元素(E,F)都分别与(A,B$\cap $N)形成二元组:
((E,F),(A,B$\cap $N)).
即是子背景的概念格Hasse图的一个边,将其送入L.处理完S的一个元素,再处理下一个元素,最终所有最大元素都处理完毕时,输出D及(D,L)就是子背景的全部概念及其Hasse图.
具体算法如下:
算法. 概念格多属性渐减式构造算法.
输入:背景K=(U,M,I),概念格B(K)及减少的属性集D;
输出:子背景K1=(U,N,I$\cap $UxN)的全部概念D及其Hasse图(D,L),这里,N=M-D.
方法:
1. N:=M-D
S:={(g(N),f(g(N)))},
D:=∅
L:=∅
2. WHILE S≠∅
3. S[0]移到(A,B)
4. P:=∅
5. D:=D$\cup ${(A,B$\cap $N)}
6. FOR (A,B)的每个直接父概念(C,D)
7. P1:=(g(D$\cap $N),f(g(D$\cap $N)))
8. P2:=(g(D$\cap $N),f(g(D$\cap $N))$\cap $N)
9. IF P1不曾在S中 THEN
10. P1加到S尾
11. END IF
12. $P:=P\overset{\circ }{\mathop{\cup }}\,\{{{P}_{2}}\}$//这里,$\overset{\circ }{\mathop{\cup }}\,$是超集吸收的并
13. END FOR
14. FOR P中的每个元素(E,F)
15. L:=L$\cup ${((E,F),(A,B$\cap $N))}
16. END FOR
17. END WHILE
18. 输出D
19. 输出(D,L)
其中,步骤1是初始化;步骤2~步骤17的WHILE循环是依次处理S中的各个最大元素,其中,
· 步骤3是将S的队首从S移出放入(A,B),即:将外延放入A,将内涵放入B;
· 步骤4是将P清空,为收集(A,B)对应的子背景概念(A,B$\cap $N)的直接父概念做准备;
· 步骤5是将(A,B)对应的子背景概念(A,B$\cap $N)送入子背景的概念集合D;
· 步骤6~步骤13的FOR循环是考察(A,B)的每个直接父概念(C,D),查找(A,B$\cap $N)的直接父概念,其中,
 步骤7、步骤8是求(C,D)所在等价类的最大元素及其对应的子背景概念(g(D$\cap $N),f(g(D$\cap $N)))及(g(D$\cap $N),f(g(D$\cap $N))$\cap $N),并分别放入P1及P2;
步骤7、步骤8是求(C,D)所在等价类的最大元素及其对应的子背景概念(g(D$\cap $N),f(g(D$\cap $N)))及(g(D$\cap $N),f(g(D$\cap $N))$\cap $N),并分别放入P1及P2;
 步骤9~步骤11是判定P1作为最大元素是否曾在S中,如果不在,则加到S队尾;
步骤9~步骤11是判定P1作为最大元素是否曾在S中,如果不在,则加到S队尾;
 步骤12是将P2按超集吸收原则并入P,记号$\overset{\circ }{\mathop{\cup }}\,$表示超集吸收的并,即:求并集时,P中是P2的超集的元素都删掉,如果P2是P中某个元素的超集,则P2删掉.这样,步骤6~步骤13的FOR循环结束时,P中将是(A,B$\cap $N)的全部直接父概念;
步骤12是将P2按超集吸收原则并入P,记号$\overset{\circ }{\mathop{\cup }}\,$表示超集吸收的并,即:求并集时,P中是P2的超集的元素都删掉,如果P2是P中某个元素的超集,则P2删掉.这样,步骤6~步骤13的FOR循环结束时,P中将是(A,B$\cap $N)的全部直接父概念;
· 于是,在步骤14~步骤16的FOR循环中,将它们与(A,B$\cap $N)形成边送入L.
整个WHILE循环结束后,D将是子背景的全部概念,(D,L)将是子背景概念格的Hasse图.
定理6. 概念格多属性渐减式构造算法的时间复杂度是O(cxmxu).这里,$c=|B(K)|$是所有概念的个数, u=|U|是对象的个数,m=|M|是属性的个数.
证明:步骤2~步骤17的WHILE循环的次数是原背景最大元素的个数(也即子背景概念的个数),显然小于原背景所有概念的个数$|B(K)|$.步骤6~步骤13的FOR循环的次数是(A,B)的直接父概念的个数,按文献[20], 该数小于|B|,显然,最不利的情况是小于|M|.在此循环中,计算P1需要|D$\cap $N|次交运算及|g(D$\cap $N)|次交运算,显然, 最不利的情况是小于|M|+|U|,在P1基础上计算P2需要1次交运算.步骤12在求并运算的同时还要做|P|次子集隶属关系的判定,|P|小于(A,B)的直接父概念的个数,显然,最不利的情况是小于|M|.同理,步骤14~步骤16的FOR循环的次数最不利的情况是小于|M|,于是,整个算法的运算次数是
$O(|B(K)|\times (|M|\times (|M|+|U|+|M|)+|M|))$
由于在实际问题中总是|M|<|U|,所以:
O(|M|+|U|+|M|)=O(|U|).
于是,
O(|M|x(|M|+|U|+|M|))=O(|M|x|U|),O(|M|x(|M|+|U|+|M|)+|M|)=O(|M|x|U|).
这样,整个算法的时间复杂度是
$O(|B(K)|\times |M|\times |U|)=O(c\times m\times u).$
我们以例1中的背景K及D=bdeh来对算法1进行验证.
初始化
N=M-D=acq,S={(7,acehq)},即,S={#12},D=∅,L=∅
WHILE S≠∅
#12概念
(A,B)=(7,acehq),(S=∅),P=∅,D={(7,acq)}
FOR #12的每个直接父概念
#10概念
P1=(12467,a),P2=(12467,a),S={(12467,a)}即S={#2},P={(12467,a)}
#11概念
P1=(57,cehq),P2=(57,cq),S={(12467,a),(57,cehq)},即,S={#2,#11},P={(12467,a),(57,cq)}
ENDFOR
FOR P中的每个元素(E,F):
L={((12467,a),(7,acq)),((57,cq),(7,acq))}.
ENDFOR
#2概念
(A,B)=(12467,a),(S={(57,cehq)}),即,(S={#11}),P=∅,D={(7,acq),(12467,a)}
FOR #2的每个直接父概念
#1概念
P1=(12345678,∅),P2=(12345678,∅),S={(57,cehq),(12345678,∅)}即S={#11,#1}
P={(12345678,∅)}
ENDFOR
FOR P中的每个元素(E,F):
L={((12467,a),(7,acq)),((57,cq),(7,acq)),((12345678,∅),(12467,a))}.
ENDFOR
#11概念
(A,B)=(57,cehq),(S={(12345678,∅)}),即,(S={#1}),P=∅,D={(7,acq),(12467,a),(57,cq)}
FOR #11的每个直接父概念
#7概念
P1=(12345678,∅),P2=(12345678,∅),S={(12345678,∅)}即S={#1},P={(12345678,∅)}
#4概念
P1=(357,c),P2=(357,c),S={(12345678,∅),(357,c)}即S={#1,#4},P={(357,c)} //超级吸收
ENDFOR
FOR P中的每个元素(E,F):
L={((12467,a),(7,acq)),((57,cq),(7,acq)),((12345678,∅),(12467,a)),((357,c),(57,cq))}.
ENDFOR
#1概念
(A,B)=(12345678,∅),(S={(357,c)}),即,(S={#4}),P=∅,
D={(7,acq),(12467,a),(57,cq),(12345678,∅)}.
FOR #1的每个直接父概念
无,P1=nil,P2=nil,S={(357,c)},即,S={#4},P=∅
ENDFOR
FOR P中的每个元素(E,F):
L={((12467,a),(7,acq)),((57,cq),(7,acq)),((12345678,∅),(12467,a)),((357,c),(57,cq))}.
ENDFOR
#4概念
(A,B)=(357,c),(S=∅),P=∅,D={(7,acq),(12467,a),(57,cq),(12345678,∅),(357,c)}
FOR #4的每个直接父概念
#1概念
P1=(12345678,∅),P2=(12345678,∅),S=∅,P={(12345678,∅)}
ENDFOR
FOR P中的每个元素(E,F):
L={((12467,a),(7,acq)),((57,cq),(7,acq)),((12345678,∅),(12467,a)),((357,c),(57,cq)),((12345678,∅),(357,c))}.
ENDFOR
ENDWHILE
我们看到:最终的结果D及L与例2中的子背景直接求得的概念及概念格完全一致,而且删除了3个属性算法也只需执行一次.
5. 后 记在减少属性m的渐减式构造算法中,对于原背景的概念(A,B)曾定义[20]:
(1) 若m$\notin $B,则称该概念为保留概念;
(2) 若m$\in $B,但B-{m}不再是任何概念的内涵,则称该概念为更新概念;
(3) 若m$\in $B,而B-{m}是某个概念(C,D)的内涵,则称该概念为删除概念,称(C,D)为该概念的删除基.
这3个定义可根据以下原理转化为另一种等价形式.由于B-{m}⊆f(g(B-{m}))⊆f(g(B)),而f(g(B))=B,所以B-{m}⊆f(g(B-{m}))⊆B,但B-{m}与B最多只差一个元素,所以,或:
f(g(B-{m}))=B-{m}
(11)
f(g(B-{m}))=B
(12)
对于以上定义的第2种情况,即更新概念的情况,公式(11)将不成立,因为f(g(B-{m}))=B-{m}意味着B-{m}是内涵,与B-{m}不再是任何概念的内涵矛盾,所以这时只能是公式(12)f(g(B-{m}))=B成立,于是这时:
g(B-{m})=g(f(g(B-{m})))=g(B)=A.
对于以上定义的第3种情况,即删除概念的情况,显然,公式(11)f(g(B-{m}))=B-{m}成立,即,这时D=B-{m}=f(g(B-{m}))及C=g(B-{m}).而且公式(12)f(g(B-{m}))=B将不成立,但f(A)=B,所以g(B-{m})≠A.这样,前面的3种情况等价于:
(1) 若m$\notin $B,则称该概念为保留概念;
(2) 若m$\in $B,但g(B-{m})=A,则称该概念为更新概念;
(3) 若m$\in $B,而g(B-{m})≠A,则称该概念为删除概念,且删除基为(g(B-{m}),f(g(B-{m}))).
与减少一个属性m对照,我们这里减少的是多个属性,即,减少的是一个属性集合D.
于是,m$\notin $B对应D$\cap $B=∅,g(B-{m})=A对应g(B-D)=A.若令N=M-D,则对应g(B$\cap $N)=A.
于是,与这3个等价定义对照,在这里是对于原背景的一个概念(A,B):
(1) 保留概念是D$\cap $B=∅(或B⊆N);
(2) 更新概念是D$\cap $B≠∅(或B∨N),但g(B$\cap $N)=A;
(3) 删除概念是D$\cap $B≠∅(或B∨N),且g(B$\cap $N)≠A,且删除基为(g(B$\cap $N),f(g(B$\cap $N))).
另外,对于第1种情况,显然g(B$\cap $N)=g(B),于是也有g(B$\cap $N)=A.这样,对于第1种、第2种这两种情况都有A=g(B$\cap $N),进而B=f(g(B$\cap $N)).这样,(A,B)=(g(B$\cap $N),f(g(B$\cap $N))).于是,由定理4知,(A,B)是最大元素.所以,我们这里的最大元素是保留概念及更新概念,B⊆N时是保留概念,B∨N时是更新概念,不是最大元素的概念都是删除概念.另外,由定理4得知,删除基就是删除概念所在等价类的最大元素.
例如,对于例1中的K及N,概念格如图1所示,概念格的等价类如图2所示,最大元素如图4所示.其中,#1,#2,#4是保留概念,#11,#12概念是更新概念,其他概念都是删除概念.#5,#6,#8,#9,#10的删除基是#2概念,#3,#7的删除基是#1概念,#13的删除基是#12概念.
减少一个属性时,一个删除基只有一个删除概念;减少多个属性时,一个删除基有多个删除概念.即:每个等价类中最大元素是删除基,其他众多元素都是删除概念.例如,例2中的删除基#2概念有多达5个删除概念:#5,#6,#8,#9,#10.这样,减少多个属性时比减少一个属性时的删除概念要多许多.由于要删除的概念多,所以不宜采用逐个删除概念、逐个删除Hasse图边的方法.我们这里是采用在原概念格的基础上获取各个最大元素(其对应概念存入D),并进而获取Hasse图边(存入L)的方法,大大缩小了对原背景概念的考察范围.例如,用本文的算法求例2中的子背景的概念格时,#5,#6,#8,#9概念以及#3概念都不会被涉及、不会被考察,并且因它们没被送入D而自动被删除;同样,很多Hasse图的边因不会被送入L而自动被删除.由于在这种算法中只需要区分最大元素及非最大元素,而区分保留概念、更新概念、删除概念的意义不太大,所以在本文算法中没做这方面的区分.本文给出的概念格多属性渐减式构造算法与文献[20]中的概念格减少单属性渐减式构造算法具有相同的时间复杂度,然而减少多个属性时,文献[20]的算法需要执行多次,本文算法只需执行一次.
| [1] | Wille R. Restructuring lattice theory:An approach based on hierarchies of concepts. Rival I. Ordered Sets. Dordrecht-Boston:Reidel, 1982. 445-470. |
| [2] | Jiang P, Ren SB, Lin J. Using formal concept analysis for software engineering. Computer Technology and Devlopment, 2008, 18(4):127-129, 213(in Chinese with English abstract). |
| [3] | Chen X, Wu Y. Mining association rules of geographic information system based on concept lattice. Journal of Computer Application, 2011,31(3):686-689(in Chinese with English abstract). |
| [4] | Xie LM, Li JM. Application research of concept lattice in intrusion detection. Computer Engineering and Design, 2010,31(5):979-981, 998(in Chinese with English abstract). |
| [5] | Xi HD, Yan H. The application of concept lattice in Web-log mining. Applies Computer Systems, 2006,15(9):21-24(in Chinese with English abstract). |
| [6] | Xu T, Xu B. Application of concept lattice of customers group clustering. Modern Computer, 2008,285(6):70-73(in Chinese with English abstract). |
| [7] | He LL, Bai HT, Zhang JC. Aspect mining using concept analysis. Computer Science, 2005,32(11):155-157(in Chinese with English abstract). |
| [8] | Liu L, Zhang Y, Li M, Yang DS. Study of dynamic knowledge bases and concept lattices applied to intelfigence disease diagnosis. Computer Engineering and Appfications, 2007,43(28):233-236(in Chinese with English abstract). |
| [9] | Yin JH, Li GQ, Chen Y, Deng M. A spatial clustering method based on concept lattices. Applies Computer Systems, 2011,20(6):103-108(in Chinese with English abstract). |
| [10] | Bal M, Sever H, Kalıpsız O. Modeling the symptom-disease relationship by using rough set theory and FormalConcept analysis. Proc. of the World Academy of Science, Engineering and Technology, 2007,26(12):517-521. |
| [11] | Shen L, Wang LM. Analysis of stability-based concept lattice for mining Folksonomy. Computer Engineering and Design, 2012, 33(3):1213-1217(in Chinese with English abstract). |
| [12] | He YQ, Li JF. Permission management of RBAC based on concept lattice. Journal of Henan University(Natural Science), 2011, 41(3):1832-1844(in Chinese with English abstract). |
| [13] | Xu JQ, Peng X, Zhao WY. An evolution analysis method based on fuzzy concept lattice and source code analysis. Chinese Journal of Computers, 2009,32(9):308-311(in Chinese with English abstract). |
| [14] | Li LF, Zhang DX. The application of concept lattice theory in the reduction of the proposition set in two-valued propositional logic. Acta Electronica Sinaca, 2007,35(8):1538-1542(in Chinese with English abstract). |
| [15] | Godin R, Missaoui T, Alaui H. An incremental concept formation algorithm based on Galois(concept) lattices. Computational Intelligence, 1995,11(2):246-267. |
| [16] | van der Merwe D, Obiedkov S, Kourie D. AddIntent:A new incremental algorithm for constructing concept lattices. In:Proc. of the 2nd Int'l Conf. on Formal Concept Analysis. LNCS 2961, Berlin:Springer-Verlag, 2004. 372-385. |
| [17] | Zhi HL, Zhi DJ. Theory and algorithm of concept lattice incremental construction based on attributes. Computer Engineering and Application, 2012,48(26):17-21(in Chinese with English abstract). |
| [18] | Andrews S. In-Close, a fast algorithm for computing formal concepts. In:Proc. of the 17th Int'l Conf. on Conceptual Structures(ICCS). Moscow:CEURWS, 2009. 1-14. |
| [19] | Liu ZT, Qiang Y, Zhou W, Li X, Huang ML. A fuzzy concept lattice model and its incremental construction algorithm. Chinese Journal of Computers, 2007,30(2):184-188(in Chinese with English abstract). |
| [20] | Zhang L, Zhang HL, Yin LH, Han DJ. Theory and algorithms of attribute decrement for concept lattice. Journal of Computer Research and Development, 2013,50(2):248-259(in Chinese with English abstract). |
| [21] | 蒋平,任胜兵,林鹃.形式概念分析在软件工程中的应用.计算机技术与发展,2008,18(4):127-129,213. |
| [22] | 陈湘,吴跃.基于概念格挖掘GIS中的关联规则.计算机应用,2011,31(3):686-689. |
| [23] | 谢丽明,李建民.概念格在入侵检测中的应用.计算机工程与设计,2010,31(5):979-981,998. |
| [24] | 习慧单,严晖.概念格在Web日志挖掘中的应用.计算机系统应用,2006,15(9):21-24. |
| [25] | 许涛,徐彬.概念格在客户群聚类中的应用.现代计算机,2008,285(6):70-73. |
| [26] | 何丽莉,白洪涛,张家晨.用概念格方法挖掘Aspect.计算机科学,2005,32(11):155-157. |
| [27] | 刘玲,张永,李明,杨德三.动态知识库和概念格在病症智能诊断中的应用.计算机工程与应用,2007,43(28)233-236. |
| [28] | 殷俊华,李光强,陈翼,邓敏.基于概念格的空间聚类方法.计算机系统应用,2011,20(6):103-108. |
| [29] | 申乐,王黎明.概念格稳定性分析及其在Folksonomy中的应用.计算机工程与设计,012,33(3):1213-121. |
| [30] | 何云强,李建凤.RBAC中基于概念格的权限管理研究.河南大学学报:自然科学版,2011,41(3):1832-1844. |
| [31] | 许佳卿,彭鑫,赵文耘.一种基于模糊概念格和代码分析的软件演化分析方法.计算机学报,2009,32(9):308-311. |
| [32] | 李立峰,张东晓.概念格在二值命题逻辑命题集约简中的应用.电子学报,2007,35(8):1538-1542. |
| [33] | 智慧来,智东杰.基于属性的概念格渐进式构造原理与算法.计算机工程与应用,2012,48(26)17-21. |
| [34] | 刘宗田,强宇,周文,李旭,黄美丽.一种模糊概念格模型及其渐进式构造算法.计算机学报,2007,30(2):184-188. |
| [35] | 张磊,张宏莉,殷丽华,韩道军.概念格的属性渐减原理与算法研究.计算机研究与发展,2013,50(2):248-259. |
 2015, Vol. 26
2015, Vol. 26


