覆盖是代数几何研究中的重要工具,在机器学习中,基于覆盖的思想可以得到多种分类手段.在这方面,中国学者相继提出了一些很有价值的方法,而这些基于覆盖思想的方法近十几年来也在不断发展.王守觉院士提出了仿生模式识别[1],该方法以获取一类样本在空间中分布的最佳覆盖为目标.何清从几何学和拓扑学的角度出发提出一种基于超曲面的分类方法[2].该方法是以Jordan曲线定理为基础,获得若干超平面组成封闭超曲面,围成封闭区域,并利用该区域对一类样本点进行覆盖.张铃等人通过对M-P神经元几何意义的重新解读[3],将样本投影到超球面后进行分类,再用不同组的球形邻域对不同类别样本进行覆盖,提出了邻域覆盖算法.后来,两人又按照邻域覆盖算法的原则,深入地进行讨论,给出了交叉覆盖算法[4].该算法在一定意义上解决了多年来一直未解决的多层前向网络的设计问题.在之后的研究中,张燕平[5]通过引入核函数,将样本集投影到核空间中进行学习,得到更优性能的分类器.吴涛[6]对如何将所构造出的覆盖投影到核空间进行了探讨,并给出了覆盖融合的方法.为了提高分类器的泛化能力,同时保持较高的识别准确率,吴涛等人[7]考虑从简化学习算法的复杂度入手,提出了多侧面递进算法.贾瑞玉等人则结合粒子群优化(PSO)具有的全局搜索能力,提出一种PSO覆盖算法[8].后来,陈洁等人提出一种分层覆盖算法[9]来确定覆盖算法分层结构的层数.该算法主要用模糊等价关系构建了基于模糊商空间理论的分层结构,并通过覆盖树来最终模拟神经网络的深层结构.文献[10]则将构造性覆盖算法和反向测试相结合来处理多示例问题,创新性地提出了一种新的多示例学习方法,利用该示例选择方法可以高效提取最具有代表性的正确示例,同时排出错误示例,从而成功提高了多示例学习的效率.
上述研究基本上都是在欧氏空间上用覆盖思想来处理分类问题.为了进一步提高覆盖算法的性能,我们在文献[11]中提出了多连通覆盖学习算法,主要是根据李群的连通性质,将具有不同类别特征的研究对象映射到多连通李群空间,并从各个单连通李群空间上连线的同伦等价[12]出发,运用覆盖的思想寻找对应不同类别的最优道路等价表示,从而用各个相对最优道路表示来呈现研究对象的类别信息.然而,算法学习出的道路等价表示的优劣性直接关系到了样本最后的分类效果.为了进一步提高分类效果,本文针对多连通覆盖学习算法,通过优化算法提高道路等价表示覆盖效果的同时,减少等价道路的相对距离,得到相对最优道路等价表示来覆盖整个多连通李群空间,从而在不增加算法运行复杂度的基础上提高算法的分类性能.
本文第1节简单概括多连通覆盖学习算法的基本思想.第2节提出并分析基于多连通覆盖学习算法的3种优化算法.第3节通过两个数据集上的实验来验证本文算法.第4节给出结论与展望.
1 多连通覆盖算法思想本节简单介绍文献[11]中提出的多连通覆盖学习算法的思想.连通是拓扑学的概念[13],而连通李群属于拓扑群,其几何性质的平移不变性和旋转不变性可以将李群空间样本的连通性更好地表示出来[14, 15, 16, 17, 18].举例说明,现在要对MPEG7_CE-Shape01_Part_B图像库上的样本进行分类,按照算法思想,首先将样本集X映射到多连通李群空间[19, 20]上得到新的样本集X'.如图 1所示,在此李群空间G上,任意两个样本点${X'_1},{X'_2}$,参数分别为(r1,r2,…, rg),(s1,s2,…,sg).李群的局部性质由无穷小元素的性质决定,用无穷小元素β1左乘${X'_1}$,即得到${X'_1}$的近邻元素${\beta _1}{X'_1}{\rm{,}}$而左乘无穷小元素β1,其实就是对${X'_1}$中局部参数的微小变化,即得到${\beta _1}{X'_1}$的参数为$({r'_1},{r_2},...,{r_g}){\rm{.}}$对得到的近邻元素${\beta _1}{X'_1}$,继续左乘无穷小元素β2,得到近邻元素${\beta _2}{\beta _1}{X'_1}$,参数为$({r'_1},{r'_2},...,{r_g}){\rm{.}}$以此类推,对元素R左乘无穷多个无穷小元素后,得元素${X''_1}$,参数变为$({r'_1},{r'_2},...,{r'_g}){\rm{.}}$若$({r'_1},{r'_2},...,{r'_g}) = ({s_1},{s_2},...,{s_g}){\rm{,}}$则${X''_1}$即为${X'_2}{\rm{.}}$所以,对元素${X'_1}$左乘的无穷多个无穷小元素即构成了连接李群空间上两个样本点${X'_1},{X'_2}$之间的一条连线.

|
Fig.1 Attachment between two samples on the connected space 图 1 连通空间上两个样本之间的连线 |
由于同类样本元素具有相似或相等的一组独立实参数,则同类样本之间的连线可以连续地互移(如图 2中的l1,l2,l3,l4,p1,p2,p3,p4),同类样本所属的李群空间任一闭道路同伦于0,即,构成单连通李群空间.单连通李群空间上的所有样本点对应的道路同伦等价(如图 2中的l1,l2,l3,l4同伦等价,p1,p2,p3,p4同伦等价),多个单连通李群空间构成多连通李群空间(如图 2中S1,S2,S3构成多连通李群空间G).由于每一个道路等价类可以表示一个单连通李群,则多连通李群即可以用多个道路等价类表示.因此,算法的研究目标就是针对多连通李群样本空间上的每一个单连通李群,学习出一条相对道路表示作为该单连通李群中所有道路的一个覆盖,最后用代表各个单连通李群空间道路特征的道路表示集合作为整个多连通李群样本空间的一个覆盖.

|
Fig.2 A plurality of simply connected Lie group spaces form a multiply connected Lie group space 图 2 多个单连通李群空间构成多连通李群空间 |
针对研究目标,算法的步骤是:
(1) 寻找微分同胚映射将样本点映射到多连通李群空间,即,对每个样本进行特征提取构造点云,然后将点云用一组SO(2)李群矩阵的直积表示[20, 21](如图 3所示),则成功完成样本映射,具体的构造点云样本过程在我们之前的研究中已详细阐述[11].

|
Fig.3 Image library samples mapped to multiply connected Lie group space 图 3 图像库样本映射到 SO(2)多连通李群空间 |
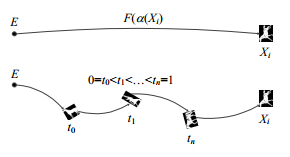
(2) 通过对每条道路进行分割,实现道路的表示.如图 4所示,α(Xi)是多连通李群空间上连接恒元点E到样本点Xi的任何一条道路,定义映射F:GaG1是相对最优道路映射,则F(α(Xi))是连接恒元点E到样本点Xi的相对最优道路.道路是连续的概念,直接表示道路有一定难度,可以设法将连续的问题离散化, 将这条道路进行分割,如图 4中道路上的割点t1,t2,…,tn,则原来的道路就可以用被这些割点分割出来的小道路表示,而割点直接决定了这些小道路的特征,故道路F(α(Xi))可直接用割点特征表示,即,
$F(a\left( {{X_i}} \right)) = F({(a\left( {{t_0}} \right))^{ - 1}}a\left( {{t_1}} \right))F({(a\left( {{t_1}} \right))^{ - 1}}a\left( {{t_2}} \right)) \ldots F({(a({t_n}_{ - 1}))^{ - 1}}a\left( {{t_n}} \right)).$
|
Fig.4 Path map discretized by cut points 图 4 被割点离散化的道路映射 |
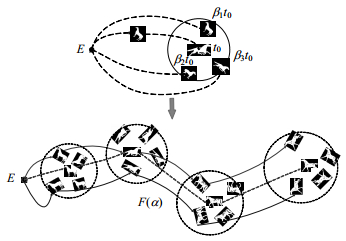
(3) 学习各分割点的邻域作为割点特征,获得各单连通域相对最优道路表示作为道路等价类的覆盖.假设对于每一个割点t,都有属于其的一个特定的无穷小元素β,由于经过βt这个邻域内的道路具有较高的关联度,因此规定这些道路是等价的(如图 5所示).则可以学习这些属于各个割点的无穷小元素β,用这些无穷小元素β表示的邻域特征作为各个割点的特征.最后,通过这些割点和对应的无穷小元素,表示相对最优道路,作为各个道路等价类的覆盖.
|
Fig.5 Learning cut points and their corresponding infinitesimal elements to represent the relatively optimal road 图 5 学习割点及对应邻域表示相对最优道路 |
以上就是多连通覆盖学习算法的思想,可见,算法的关键是如何确定相对最优道路表示.显然,只根据上述思想学习样本,我们无法保证得到的道路表示是最优的,因为首先,由于样本分布的随机性及学习样本的先后顺序会直接影响道路的构建和选择.文献[11]中的算法给出了解决方案,先计算各个割点的覆盖权值,从而选择最优割点构成道路作为覆盖表示.这样,覆盖权值最高的割点都加入到构建的道路表示中,一方面在一定程度上缩短了道路表示的相对长度,另一方面也提高了道路表示的覆盖效果.实验证明这确实是一个很好的解决方案.
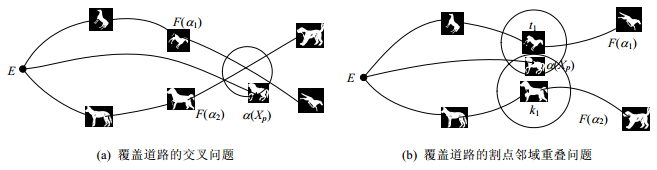
然而,仍然存在以下这些情况影响相对最优道路表示的覆盖效果:对于二维图像映射后得到的连通空间的道路,其实质是物体形态的拓扑变化过程,则两个形态相似的样本(如图 6所示),其对应的不同类的相对最优覆盖道路可能存在交叉(如图 6(a)所示),或者道路表示对应的割点及其无穷小元素确定的邻域可能重合(如图 6(b)所示).这些得到的道路表示都造成了重复覆盖,则对新样本就很难判断它属于哪一个道路覆盖,也就会造成类别的误判.接下来的工作就是要通过改进算法来解决这些问题.
|
Fig.6 Intersection problems in connected Lie group space 图 6 连通李群空间的道路交叉问题 |
为了解决上一节提出的相对最优覆盖道路可能存在交叉或者邻域重合的问题,我们考虑引入Fisher投影的思想.标准的Fisher投影[22, 23]是将样本点投影到一个比样本维数更低的超平面或直线上,使得各类别之间的类间散度尽可能地大,同时,各类的类内散度尽可能地小.所以我们考虑,若在连通道路中引入Fisher投影的思想,是否可以使得投影后单个单连通空间上的道路尽可能地靠拢,而属于不同单连通空间上的道路尽可能地分开,从而减少出现道路交叉或道路邻域重合问题的可能性(如图 7所示).

|
Fig.7 Optimization effect that Fisher discriminant method expected to reach 图 7 Fisher 判别预期达到的优化效果 |
标准Fisher投影只适用于欧氏空间,而本文中的样本需要映射到多连通李群空间,这就无法直接运用标准Fisher投影来处理.文献[21]提出了适用于李群空间的Lie-Fisher投影,其投影的目的就是在李群流形上寻找一条测地线[24],将所有样本向这条测地线投影,使投影后的新样本的类间散度和类内散度比值最大化.虽然Lie- Fisher投影适用于李群空间,但它是基于李群均值学习算法提出的投影方法,对于多连通覆盖学习算法中的道路学习起不到作用.在道路学习中,我们的最终目的同样是在李群流形上寻找一条测地线,使得投影到测地线上的各个单连通空间上的道路之间的关联度(同连通道路关联度)尽可能地增大,而不同单连通空间上的道路(异连通道路关联度)之间的关联度尽可能地减小.
设多连通李群G对应的李代数元素ω∈g,通过单参数指数映射:\mathbb {R}→G:exp(tω),t∈\mathbb {R},可在李群流形上生成一条测地线Hω,Hω是G上的一个单参数子群,它由李代数元素ω唯一确定:
${H_\omega } \buildrel \Delta \over = \{ exp(t\omega ) \in G,t \in \mathbb {R}\} .$
而给定参数t也就确定了Hω上的一个点,则可定义李群上的点到测地线上的投影:设一个样本x∈G和G上的测地线Hω,首先确定:
${t^*} = argmind(x,exp(tw)),t \in \mathbb {R},$
则exp(t*ω)即为样本点x到Hω的投影点,从几何观点来看,该投影点就是Hω上所有点中到x的测地线距离最近的那个点.令y=exp(tω)是x到Hω的投影点,则各个单连通空间上的样本点$\{ {x_{ij}}\} _{j = 1}^{{n_i}}$投影到Hω后,可得到新的点集:$\{ {y_{ij}}\} _{j = 1}^{{n_i}}{\rm{.}}$设代表第i类样本的单连通空间上用多连通覆盖学习算法[11]学习出的相对最优覆盖道路是
$F({a_i}) = F({({a_i}\left( {{c_0}} \right))^{ - 1}}{a_i}\left( {{c_1}} \right))F({({a_i}\left( {{c_1}} \right))^{ - 1}}{a_i}\left( {{c_2}} \right)) \ldots F({({a_i}({c_k}_{ - 1}))^{ - 1}}{a_i}\left( {{c_k}} \right)),$
其中,c0,c1,…,ck是道路的割点,αi表示第i类样本的单连通空间上的道路等价类[αi],将该道路表示投影到测地线Hω后得到新的道路表示:
$F'({\alpha '_i}) = F'({({\alpha '_i}({c'_0}))^{ - 1}}{\alpha '_i}({c'_1}))F'({({\alpha '_i}({c'_1}))^{ - 1}}{\alpha '_i}({c'_2}))...F'({({\alpha '_i}({c'_{k - 1}}))^{ - 1}}{\alpha '_i}({c'_k})),$
其中,${c'_0},{c'_1},...,{c'_k}$是投影后的道路割点.则同连通道路关联度可表示为
${S'_w} = \sum\limits_{i = 1}^h {\sum\limits_{j = 1}^{{n_i}} {{d^2}{{({{\alpha '}_i}({y_{ij}}),{{\alpha '}_i}({{c'}_t}))}^{ - 1}}} } ,$
其中,h表示类别个数;ni表示第i个类别的样本个数;yij表示xij在Hω上的投影;${\alpha '_i}({c'_t})$表示道路${\alpha '_i}({y_{ij}})$所在的邻域的割点所对应的道路,若邻域边界对应的无穷小元素为β',则${\alpha '_i}{({y_{ij}})^{ - 1}}{\alpha '_i}({c'_t}) \in F'({\alpha '_i}(\beta '{c'_t})).$
异连通道路关联度为
${S'_b} = \sum\limits_{i = 1}^c {{n_i}{d^2}} {({F'_{{{\mu '}_i}}},{F'_{\mu '}})^{ - 1}},$
其中,${F'_{\mu '}}$为整个多连通空间的道路密度,${F'_{{{\mu '}_i}}}$是第i个类别样本所对应的单连通空间上所有道路基于相对最优
道路各割点表示的加权期望.近似于标准Fisher的思想,在多连通空间上,同样定义Fisher准则函数:
$J(\omega ) = \frac{{{{S'}_b}}}{{{{S'}_w}}}.$
因此,算法的问题归结为寻找满足下式的一条测地线${H_{{\omega ^*}}}:$
${\omega ^ * } = \arg \min J\left( \omega \right)$
2.1 基于Fisher投影的优化算法1要计算求得上述测地线${H_{{\omega ^*}}}{\rm{,}}$本文考虑参考标准Fisher和Lie-Fisher的计算方法,即,通过对数映射将道路表示可计算化.算法的基本思想:通过对数映射,将原本多连通李群空间上的道路映射到对应的李代数空间,得到新的道路表示,则得到的李代数空间上的道路表示,就可以直接运用Lie-Fisher的计算方法来求解同类道路的关联度Sw和异类道路的关联度Sb,则优化算法1见算法1.
算法 1. 基于Fisher投影的多连通覆盖学习算法1(FMCCLA1).
输入:$\{ {X_{ij}}\} _{i = 1,2,...,s}^{j = 1,2,...,{n_i}} \in G$,G是多连通李群空间,Xij表示第i类别的第j个样本在该空间的映射,ni表示第i个分类中训练样本的个数,一共有s个分类.
输出:各个单连通空间上的经过Fisher投影后得到的相对最优道路表示${\{ F'({\alpha '_i}({c'_t}))\} _{i = 1,2,...,s}}{\rm{,}}$t对应这条相对
最优道路表示需要t个割点.
Step 1. 运用第1节提出的多连通覆盖学习算法span>(MCCLA)求出各个连通空间的道路覆盖表示:
$F({a_i}),i = 1,2, \ldots ,s.$
Step 2. 将割点对应的道路表示通过对数映射得到道路的李代数表示:
$M({a_i}) = log(F({a_i})).$
Step 3. 计算同连通道路关联度:
${S_w} = \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {{d^2}{{(M({\alpha _i}({X_{ij}})),M({\alpha _i}({c_j})))}^{ - 1}}} } = \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {{{\langle \log (F({\alpha _i}({X_{ij}}))) - \log (F({\alpha _i}({c_j})))\rangle }^{ - 1}}} } .$
其中,αi(Xij)是样本点Xij在连通空间上的对应道路,cj是Xij对应道路αi(Xij)的道路覆盖邻域对应的
割点.计算异连通道路关联度:
${S_b} = \sum\limits_{i = 1}^s {{n_i}{d^2}({F_{{\mu _i}}},{F_\mu })} = \sum\limits_{i = 1}^s {{n_i}{{\langle {F_{{\mu _i}}} - {F_\mu }\rangle }^{ - 1}}} .$
整个多连通空间上的道路密度为
${F_\mu } = \frac{1}{n}\sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {\log (F({\alpha _i}({X_{ij}})))} } .$
第i个类别样本所对应的单连通空间上所有道路基于相对最优道路各割点表示的加权期望为
${F_{{\mu _i}}} = \frac{1}{{{n_i}}}\sum\limits_{j = 1}^{{n_i}} {{r_j}\log (F({\alpha _i}({c_j})))} .$
其中,F(αi(cj))表示道路αi(Xij)所在的邻域的割点所对应的道路,rj为该邻域已覆盖的道路数目.
Step 4. 求解Sbω=λSwω,得到ω*,按${H_{{\omega ^*}}} \buildrel \Delta \over = \{ \exp (t{\omega ^*}) \in G,t \in \mathbb {R}\} $生成测地线${H_{{\omega ^*}}}{\rm{,}}$将Step1中的道路覆盖表示向测地线投影,得到新的相对最优道路表示${\{ F'({\alpha '_i}({c'_t}))\} _{i = 1,2,...,s}}.$
Step 4中的道路向测地线进行投影,即,根据求得的测地线对应的最优投影向量ω*,将MCCLA算法求得的相对最优道路表示中的割点向测地线进行投影,全部割点投影后,即可得到新的道路表示.
对于被测试样本T,首先将其映射到多连通李群空间,得到对应的道路表示α(T),α(T)可用多连通覆盖算法第1步所介绍的一组SO(2)李群矩阵的直积表示(见文献[11]),并将其映射到李代数空间,得log(F(α(T)));然后, 将该道路表示向测地线${H_{{\omega ^*}}}$投影得到新的道路表示F'(α'(T')),求该道路表示到相对最优道路表示的距离:
${l_T} = d(F'(\alpha '(T')),F'(\alpha '({c'_t})).$
设β'为割点${c'_t}$邻域边界对应的无穷小元素,则相对最优道路表示的覆盖邻域为$F'(\alpha '(\beta '{c'_t}))$,从而通过lT和道路覆盖邻域最终判定道路的类别.
2.2 基于Fisher投影的优化算法2算法1在用Fisher思想求解投影测地线时,对道路进行了对数映射,然后在对应李代数空间,用欧氏空间的计算方法来求解投影向量ω*.这样做虽然计算方便,但不可避免地会造成结果与实际相对最优道路的误差变大.为了尽可能地缩小这样的误差,本文提出优化算法2,其基本思想为:考虑将道路在多连通李群流形空间中,直接进行总体道路密度及道路关联度的计算,则优化算法2见算法2.
对于被测试样本T,
$ \bullet $ 首先将其映射到多连通李群空间,得到对应的道路表示F(α(T));
$ \bullet $ 然后,将该道路表示向测地线${H_{{\omega ^*}}}$投影得到新的道路表示F'(α'(T')),求该道路表示到相对最优道路各个割点的连接道路$F'(\alpha '{(T')^{ - 1}}\alpha '({c'_t})){\rm{,}}$判断该道路是否属于道路邻域$F'(\alpha '(\beta '{c'_t})){\rm{,}}$β'为割点${c'_t}$道路邻域边界对应的无穷小元素,从而最终判定道路的类别.
算法2. 基于Fisher投影的多连通覆盖学习算法2(FMCCLA2).
输入:$\{ {X_{ij}}\} _{i = 1,2,...,s}^{j = 1,2,...,{n_i}} \in G{\rm{,}}$G是多连通李群空间,Xij表示第i类别的第j个样本在该空间的映射,ni表示第i个分类中训练样本的个数,一共有s个分类.
输出:各个单连通空间上的经过Fisher投影后得到的相对最优道路表示${\{ F'({\alpha '_i}({c'_t}))\} _{i = 1,2,...,s}}$,t对应这条相对最优道路表示需要t个割点.
Step 1. 运用第2节提出的多连通覆盖学习算法(MCCLA)求出各个连通空间的道路覆盖表示:
$F({a_i}),i = 1,2, \ldots ,s.$
Step 2. 计算同连通道路关联度:
${S_w} = \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {{d^2}{{(F({\alpha _i}({X_{ij}})),F({\alpha _i}({c_k})))}^{ - 1}}} } = \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {\langle \log {{(F({\alpha _i}{{({c_k})}^{ - 1}}{\alpha _i}({X_{ij}}))\rangle }^{ - 1}}} } .$
其中,αi(Xij)是样本点Xij在连通空间上的对应道路,ck是Xij对应道路αi(Xij)的道路覆盖邻域对应的割点.
Step 3. 计算整个多连通空间上的道路密度为
${F_\mu } = \mathop {\arg \min }\limits_X \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{n_i}} {\langle \log (F({\alpha _i}{{({X_{ij}})}^{ - 1}}{\alpha _i}(X)))\rangle } } .$
计算各个单连通空间上的道路密度为
${F_{{\mu _i}}} = \mathop {\arg \min }\limits_{{X_i}} \sum\limits_{j = 1}^{{n_i}} {{d^2}(F({\alpha _i}({X_i})),F({\alpha _i}({c_j})))} = \mathop {\arg \min }\limits_{{X_i}} \sum\limits_{j = 1}^{{n_i}} {\langle \log (F({\alpha _i}{{({c_j})}^{ - 1}}{\alpha _i}({X_i}))\rangle } ,$
其中,F(αi(cj))表示道路F(αi(Xij))所在邻域的割点在连通空间上所对应的道路.
Step 4. 计算异连通道路关联度:
${S_b} = \sum\limits_{i = 1}^s {{n_i}{d^2}({F_{{\mu _i}}},{F_\mu })} = \sum\limits_{i = 1}^s {{n_i}{{\langle \log (F_\mu ^{ - 1}{F_{{\mu _i}}})\rangle }^{ - 1}}} .$
Step 5. 求解Sbω=λSwω,得到ω*,按${H_{{\omega ^*}}} \buildrel \Delta \over = \{ \exp (t{\omega ^*}) \in G,t \in \mathbb {R}\} $生成测地线${H_{{\omega ^*}}}{\rm{,}}$将Step1中的道路覆盖表示向测地线投影,得到新的相对最优道路表示${\{ F'({\alpha '_i}({c'_t}))\} _{i = 1,2,...,s}}.$
2.3 基于Fisher投影的优化算法3优化算法1在计算不同单连通空间上道路之间的关联度时,有:
${S_b} = \sum\limits_{i = 1}^s {{n_i}{d^2}{{({F_{{\mu _i}}},{F_\mu })}^{ - 1}}} .$
${F_{{\mu _i}}}$表示的是第i个类别样本所对应的单连通空间上所有道路基于相对最优道路各割点表示的加权期望, 割点正是由所有道路经过MCCLA算法训练出来的,相对最优道路表示的特征由组成它的割点特征呈现,故可以直接用割点的加权期望来表示${F_{{\mu _i}}}$,达到同样的效果,同时减少算法的复杂度,即可对算法1做局部修改,有:
${F_{{\mu _i}}} = \frac{1}{t}\sum\limits_{j = 1}^{{n_i}} {{r_j}\log (F({\alpha _i}({c_j})))} ,$
其中,t为该单连通空间用MCCLA算法训练出的道路覆盖的割点的总个数,其他算法步骤不变.
2.4 优化算法的时间复杂度下面考虑3种优化算法的时间复杂度,由于优化算法都要先运用多连通覆盖学习算法(MCCLA)求出各个连通空间的道路覆盖表示,而文献[11]中已交代,该算法的时间复杂度在O(n2)~O(n3)之间,为了更好地比较3种优化算法的时间复杂度,本文中考虑算法优化部分的时间复杂度.
定理 1. 3种优化算法优化处理的时间复杂度均为O(n).
证明:在算法FMCCLA1中,Step 2求多连通空间上所有道路的李代数映射是一对一映射,所用时间代价是n;Step 3计算总体道路密度共n条道路,代价为n,s个单连通域均计算${F_{{\mu _i}}}{\rm{,}}$代价仍相当于计算总道路数,为n,则计算Sw代价也为n,计算Sb代价为s,所以Step 3总代价为3×n+s;Step 4计算ω*需要时间代价为1,然后映射所有道路到测地线需要时间代价为n,则Step 4需要总代价n+1,故优化算法1的总时间代价是:
${T_1} = n + 3n + s + 1 + n = 5n + s + 1 = O\left( n \right).$
因此,算法FMCCLA1的时间复杂度为O(n).
在算法FMCCLA2中,Step 2计算Sw,也和每条道路对应,时间代价为n;Step 3中,在计算道路密度时,相当于要计算样本的内均值,即,用到了迭代,设每次计算道路密度用到的迭代次数都是k次,则计算总道路密度时间代价为kn,计算各个连通空间道路密度为kni,所以Step 3总时间代价为$kn + \sum\limits_{i = 1}^s {k{n_i}} = 2kn$;Step 4计算Sb代价为s;
Step 5时间代价为n+1,故优化算法2总时间代价为
${T_2} = n + 2kn + s + n + 1 = \left( {2k + 2} \right)n + s + 1 = O\left( n \right).$
因此,算法FMCCLA2的时间复杂度为O(n).
优化算法3只是对优化算法1的局部修改,不影响各个步骤的时间代价计算,故总时间复杂度仍为O(n),定理得证. □
3 实验及结果分析我们通过几个实验把本文中的3个优化算法和原算法就分类性能做比较,以表现优化算法的分类优势.第1个实验选用的数据集是MPEG7_CE-Shape01_Part_B图像库[25],第2个实验选用的数据集是MNIST手写体数据集[26].
3.1 MPEG7_CE-Shape01_Part_B图像库上样本的分类MPEG7_CE-Shape01_Part_B图像库是一个图像模拟库,是用于图像的形状模板,库里包含了许多物体的模板图,可以用于物体形状特征的研究,每个物体都有20个不同样式的模板图.文献[11]中也在此数据集上将多连通李群覆盖学习算法(MCLGC-LA)与李群空间上的其他两种算法进行了对比实验,分类性能良好.本文同样在此数据集上把基于多连通覆盖学习算法(MCCLA)的3种优化算法与原算法以及领域覆盖算法(NCA)、交叉覆盖算法(ACA)在分类性能上做对比,体现优化算法的性能优势.
3.1.1 两类样本的分类首先,在此图像库上将前面提出的算法及其优化方案针对两类样本进行对比实验.选取horse和camel两种模板,对这两类图像进行分类,由于每个物体一共20个不同样式的模板图,要进行实验,首先需要划分训练样本和测试样本,文献[11]中直接主观选取每类样本的前15个模板图作为训练样本,剩下的5个模板图作为测试样本进行实验.这样主观地确定训练样本和测试样本虽然也能达到实验的目的,但是并不能保证算法的分类结果达到最优.因此,需要通过实验确定分别选取的训练样本数和测试样本数.选取两个模板(仍然以horse和camel为例),分别选取训练样本数分别为1,2,3,…,19,剩下的为测试样本进行实验.
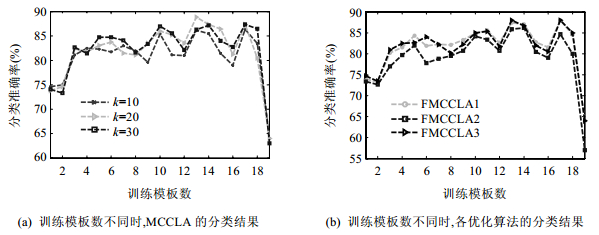
图 8(a)是多连通覆盖学习算法(MCCLA)在训练样本数不同时对horse和camel两类物体的分类结果,3条线分别对应着k值取10,20,30的情况.针对每一个不同的训练模板数,算法都重复5次求分类准确率,用5次求值的平均值作为最后的结果显示.从图中可以看出,训练模板数为13、测试模板数为7时,无论k取何值,MCCLA算法都能显示出最佳的分类性能.图 8(b)是MCCLA的优化算法在训练样本数不同时对horse和camel两类物体的分类结果,其中,随机选取的样本点个数k=20.从图中清晰可见:各个优化算法在训练模板数为13时,均能达到最好的分类效果.因此,在此数据集上的比较实验确定训练样本数为13,测试样本数为7.
|
Fig.8 Results of different algorithms based on different training templates 图 8 训练模板不同时几种算法的分类结果 |
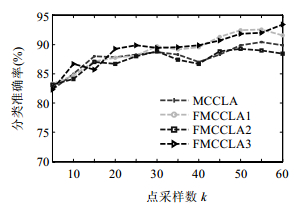
确定了训练模板数和测试模板数,我们就可以进行实验来比对算法的性能了.由于样本个数略显单薄,可以对每个模板图取样时重复10次随机取样构成k点云样本,则每类物体均有130个训练样本、70个测试样本,即,一共260个训练样本、140个测试样本.先选取horse和camel两个比较相近的动物模板,随机选择k个点构成点云,当k取不同值时,针对每种算法,同样都重复5次随机选择k个点,并对最后的分类识别率取平均值.先比较原算法和优化算法的分类结果,如图 9所示.从图中可以看出,4种算法在此研究对象上都能保持较高的分类准确率,基本维持在80%以上.3种基于Fisher投影的优化算法总体来说分类效果优于原来的多连通覆盖算法,除了优化算法FMCCLA2和MCCLA算法分类效果差不多之外,FMCCLA1和FMCCLA3分类效果总体上都优于MCCLA算法,特别是当k大于25以后,这两种优化算法都一直保持着分类的优势,且分类准确率基本已达到90%以上.
|
Fig.9 Results of MCCLA and its optimization algorithms on horse and camel 图 9 优化算法与原算法对 horse 和 camel 的分类结果 |
图 10是加入两种经典的覆盖学习算法后对cattle和elephant分类的比较结果,显然,后4种算法的分类准确率远远高于两种经典覆盖算法,且MCCLA算法及其优化算法的对应曲线相对来说也更加平滑,表现出算法更好的稳定性.在几种基于Fisher的优化算法中,除了FMCCLA2算法在此研究对象上的分类性能不是很好之外,FMCCLA1算法和FMCCLA3算法的分类效果都明显优于原算法MCCLA.特别是FMCCLA3算法的分类优势极其明显,一直处于相当高的水平;且相对于其他几种优化算法也更加稳定,其对应曲线的波折明显较小.

|
Fig.10 Results of different algorithms on cattle and elephant 图 10 几种算法对 cattle 和 elephant 的分类结果 |
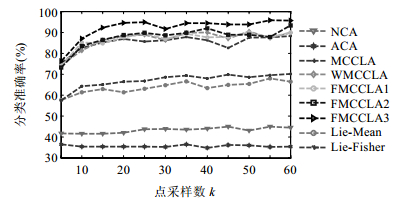
实验任意选取MPEG7_CE-Shape01_Part_B数据集上的4类物体(horse,bat,beetle,bone)的模板作为样本,研究本文算法对多个类别样本的分类情况.基于前一节的分析,对每个模板图取样时重复5次随机取样构成k点云样本,这样,每类模板图共有65个训练样本、35个测试样本,即,共有260个训练样本、140个测试样本.然后,应用MCCLA算法及其优化算法FMCCLA与两种经典的覆盖学习算法(NCA和ACA)以及文献[21]提出的经典李群上的均值算法(Lie-Mean)和改进后的Lie-Fisher算法分别对样本进行分类,得到的结果如图 11所示.
|
Fig.11 Results of different algorithms on horse, bat, beetle and bone 图 11 几种算法对 horse,bat,beetle,bone 分类的比较结果 |
从图 11明显可以看出,两种经典的覆盖学习算法在分类这4类模板图时分类效果并不是很好,分类准确率只有40%左右;两种经典李群上的均值算法(Lie-Mean)和改进后的Lie-Fisher算法分类效果虽然明显好于NCA和ACA,但分类准确率也只有70%左右;而MCCLA算法及其优化算法的分类准确率最低也在75%左右,特别在k大于等于15以后,准确率则一直保持在85%以上,分类优势相当明显.而在MCCLA算法和其优化算法中,3种FMCCLA算法从k=5开始就一直比原算法表现出明显的分类优势,其中,FMCCLA3分类准确率一直保持最高,特别当k大于等于15以后,其分类结果一直保持在90%以上.
3.2 手写体数据集上样本的分类本实验采用MNIST数据集,该数据集属于二维真实图像,每个手写数字都是28×28的256阶灰度图片.同样地,我们采用文献[11]的方法,将数据集的形状信息映射到SO2多连通李群空间,构造新的样本进行学习分类.图 12是对MNIST数据集上的数字2和9的一个样本取不同k个点构成的点云样本,这些点云样本将代表原来的样本加入到算法中进行计算.

|
Fig.12 Point cloud samples of different k value based on digital 6 and 9 图 12 以数字 2 和 9 为例提取的不同 k 值的点云样本 |
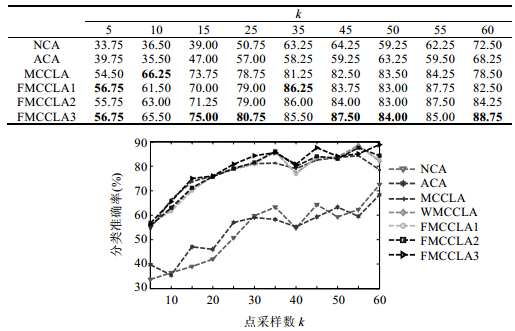
本实验直接考虑算法对多个类别样本的分类情况,将本文提出的优化算法与原算法及两种经典覆盖学习算法进行对比实验.首先选取1,3,5,7这4个数字作为分类样本,分别从train1,train3,train5,train7中各随机选取50个,一共200个数字作为训练集,再从test1,test3,test5,test7中各随机选取20个,一共80个数字作为测试集,然后,应用几种算法对样本进行分类,得到的结果如图 13所示.
|
Fig.13 Results of different algorithmson digital 1, 3, 5 and 7 图 13 几种算法对数字 1,3,5,7 分类的比较结果 |
从图 13可以清楚地看出,MCCLA及其优化算法的分类准确率一直比经典的覆盖学习算法高20个百分比以上;且它们对应的曲线也比邻域覆盖和交叉覆盖算法对应的曲线平滑,即,算法的稳定性更高.同时,优化算法的分类性能总体都优于原算法,特别是当k≥20时优势比较明显.在几种优化算法FMCCLA中,FMCCLA3总体保持最优,而其他几种优化算法的曲线分布近似重合,即,它们的分类性能相似.
图 14给出了上述这些算法以及两种李群均值算法(Lie-Mean和Lie-Fisher)在数字2,4,6,8上分类的效果.同样,分别从train2,train4,train6,train8中各随机选取50个、一共200个数字作为训练集.在此实验中,我们增加了测试样本个数,通过更多的实际样本进一步验证算法的实用性.具体过程是:针对test2,test4,test6,test8各类别,将随机取样本数从20增加到40,一共160个数字作为测试集.可以发现:在此研究对象上,MCCLA及其优化算法仍然较两种经典覆盖学习算法以及两种李群均值算法有明显的分类优势,MCCLA算法及其优化算法整体的识别率差距不大,几种优化算法总体分类性能一直略高于原算法.而在几种优化算法中,FMCCLA3一直保持分类效果最优.

|
Fig.14 Results of different algorithms on digital 2, 4, 6 and 8 图 14 几种算法对数字 2,4,6,8 分类的比较结果 |
综上所述,本文针对之前研究得出的多连通覆盖学习算法中的道路交叉问题,从进一步优化算法中的相对最优道路表示出发,用Fisher投影的思想,通过多个层面设计出相应的道路优化算法.本文通过在两个数据集上的多组实验,一方面表明,多连通覆盖学习算法比欧氏空间上的邻域覆盖算法及交叉覆盖算法在样本维数不太高时具有更优的分类效果和维数收敛性;另一方面表明,本文提出的优化算法分类性能明显优于原算法,同时,本文提出的算法在这两个数据集上也比经典李群上的均值算法(Lie-Mean)以及改进后的Lie-Fisher算法分类性能更优.本文主要是从预防拓扑空间道路交叉的角度优化算法,我们期望在今后的研究中,可以从其他方面进一步优化算法.
致谢 在此,我们向对本文的工作给予支持和建议的同行,尤其是实验室的同学们表示感谢.
| [1] | Wang SJ. Bionic (Topological) pattern recognition—A new model of pattern recognition theory and its applications. Acta Electronica Sinica, 2002,30(10):1417-1420 (in Chinese with English abstract) . |
| [2] | He Q, Shi ZZ, Ren LA. The classification method based on hyper surface. In: Proc. of the 2002 Int’l Joint Conf. on Neural Networks. Honolulu: IEEE, 2002. 1499-1503 . |
| [3] | Zhang L, Zhang B. A geometrical representation of McCulloch-pits neural model and its applications. IEEE Trans. on Neural Networks, 1999,10(4):925-929 . |
| [4] | Zhang L, Zhang B. Across covering algorithm of multiplayer forward networks. Ruan Jian Xue Bao/Journal of Software, 1999, 10 (7):737-742 (in Chinese with English abstract). http://www.jos.org.cn/ch/reader/create_pdf.aspx?file_no=19990712&journal_id=jos |
| [5] | Zhang YP, Zhang L, Duan Z. A constructive kernel covering algorithm and applying it to image recognition. Journal of Image and Graphics, 2004,9(11):1304-1308 (in Chinese with English abstract) . |
| [6] | Wu T, Zhang L, Zhang YP. Kernel covering algorithm for machine learning. Chinese Journal of Computers, 2005,28(8):1295-1301 (in Chinese with English abstract) . |
| [7] | Wu T, Zhang FF. Multi-Side covering algorithm based on feature selection. Journal of Computer Applications, 2011,31(5): 1318- 1320 (in Chinese with English abstract) . |
| [8] | Jia RY, Ning ZZ. Particle swarm optimization covering algorithm. Computer Engineering, 2011,37(21):167-169 (in Chinese with English abstract). |
| [9] | Chen J, Zhao S, Zhang Y. Hierarchical covering algorithm. Tsinghua Science and Technology, 2014,19(1):76-81 . |
| [10] | Zhang YP, Zhang H, Wei HZ, Tang J, Zhao S. Multiple-Instance learning with Instance selection via constructive covering algorithm. Tsinghua Science and Technology, 2014,19(3):285-292 . |
| [11] | Yan C, Li FZ, Zou P. Multiply connected Lie group covering learning algorithm for image classification. Journal of Frontiers of Computer Science and Technology, 2014,8(9):1101-1112 (in Chinese with English abstract) . |
| [12] | Huang BJ. Homology and Homotopy Theory. Hefei: Science & Technology Publishing House, 2005 (in Chinese). |
| [13] | Jiang ZH. Introduction to Topology. Shanghai: Shanghai Scientific & Technical Publishers, 1978 (in Chinese). |
| [14] | Baker A. Matrix Groups: An Introduction to Lie Group Theory. New York: Spinger-Verlag, 2002 . |
| [15] | Gallier J. Notes on Differential Geometry and Lie Groups. Philadelphia: University of Pennsylvannia, 2012. |
| [16] | Gilmore R. Lie Groups, Lie Algebras, and Some of Their Applications. New York: Courier Corporation, 2012. |
| [17] | Fiori S, Tanaka T. An algorithm to compute averages on matrix Lie groups. IEEE Trans. on Signal Processing, 2009,57(12): 4734- 4743 . |
| [18] | Li FZ, Zhang L, Yang JW, Qian XP, Wang BJ, He SP. Lie Group Machine Learning. Hefei: University of Science and Technology of China Press, 2013 (in Chinese). |
| [19] | Ma ZQ. Group Theory in Physics. Beijing: Science Press, 1998 (in Chinese). |
| [20] | Yarlagadda P, Ozcanli O, Mundy J. Lie group distance based generic 3-d vehicle classification. In: Proc. of the 2008 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2008. 1-4 . |
| [21] | Gao C, Li FZ. Lie group means learning algorithm. Pattern Recognition and Artificial Intelligence, 2012,25(6):900-908 (in Chinese with English abstract) . |
| [22] | Masashi S. Local fisher discriminant analysis for supervised dimensionality reduction. In: Proc. of the 23rd Int’l Conf. on Machine Learning. Pittsburgh: ACM Press, 2006 . |
| [23] | Duda RO, Hart PE, Stork DG. Patten Classification. New York: Wiley, 2001. |
| [24] | Flecher T, Lu C, Joshi S. Statistics of shape via principal geodesic analysis on Lie groups. In: Proc. of the 2003 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2003. 95-101 . |
| [25] | Ying SH, Peng YX, Wen ZJ. Iwasawa decomposition: A new approach to 2D affine registration problem. Pattern Analysis and Applications, 2011,14(2):127-137 . |
| [26] | Žefran M, Kumar V, Croke C. Metrics and connections for rigid-body kinematics. The Int’l Journal of Robotics Research, 1999, 18 (2):242-1-242-16 . |
| [1] | 王守觉.仿生模式识别(拓扑模式识别)——一种模式识别新模型的理论与应用.电子学报,2002,30(10):1417-1420 . |
| [4] | 张铃,张钹,殷海风.多层前向网络的交叉覆盖设计算法.软件学报,1999,10(7):737-742.http://www.jos.org.cn/ch/reader/create_pdf.aspx?file_no=19990712&journal_id=jos |
| [5] | 张燕平,张铃,段震.构造性核覆盖算法在图像识别中的应用.中国图像图形学报,2004,9(11):1304-1308 . |
| [6] | 吴涛,张铃,张燕平.机器学习中的核覆盖算法.计算机学报,2005,28(8):1295-1301 . |
| [7] | 吴涛,张方方.基于特征选择的多侧面覆盖算法.计算机应用,2011,31(5):1318-1320 . |
| [8] | 贾瑞玉,宁再早.粒子群优化覆盖算法.计算机工程,2011,37(21):167-169 . |
| [11] | 严晨,李凡长,邹鹏.多连通李群覆盖学习算法在图像分类上的应用.计算机科学与探索,2014,8(9):1101-1112 . |
| [12] | 黄保军.同调与同伦原理.合肥:中国科学技术出版社,2005.16-59. |
| [13] | 江泽涵.拓扑学引论.上海:上海科学技术出版社,1978.25-169. |
| [18] | 李凡长,张莉,杨季文,钱旭培,王邦军,何书萍.李群机器学习.合肥:中国科学技术大学出版社,2013. |
| [19] | 马中骐.物理学中的群论.北京:科学出版社,1998. |
| [21] | 高聪,李凡长.李群均值学习算法.模式识别与人工智能,2012,25(6):900-908 . |
 2015, Vol. 26
2015, Vol. 26


