机器学习正面临着数据规模日益扩大的严峻挑战.传统的机器学习批处理梯度优化方法每次迭代都要遍历所有样本[1],已经不能满足快速求解机器学习优化问题的需求.由于机器学习问题通常假设样本是独立同分布的,从而随机抽取单个样本的目标函数的梯度是整个目标函数梯度的无偏估计[2],进而可用每次迭代仅处理单个或部分样本的随机优化方法来代替批处理方法[2, 3].虽然随机优化算法每一步迭代能够节省计算开销,但往往会导致较大的方差,不可避免地会影响算法的收敛速率[4].
为了减小方差对算法收敛速率的影响,Johnson等人于2013年提出一种在优化算法中采用减小方差的策略,称为SVRG(stochastic variance reduced gradient)[4].SVRG的主要思路是:在原有单个样本的梯度计算中引入修正量,该修正量由所有样本梯度的平均值组成,与仅使用单个样本梯度的标准随机优化算法相比,修正后的梯度可以明显减小方差.对于求解光滑强凸优化问题,SVRG算法能够达到最优的收敛速率,与当前主流优化方法SDCA(stochastic dual coordinate ascent)[5]和SAG(stochastic average gradient)[6]的收敛速率相同.与SDCA和SAG不同的是,SVRG不需要存储目标函数的梯度,从而减小了内存开销.另一方面,SVRG收敛速率的证明过程也更加简单,并可以应用于求解深度神经网络导致的非凸优化问题[4].
正是由于SVRG具有上述优点,Xiao等人于2014年将SVRG由求解简单的黑箱优化问题推广到具有结构信息的正则化损失函数优化问题[7],称为Prox-SVRG(proximal SVRG)[8].与SVRG不同的是,Prox-SVRG保持正则化项不变,仅对损失项的梯度进行优化.这种处理方式与当前流行的结构优化算法RDA(regularized dual average)[7]和COMID(composite objective mirror descent)[9]完全相同.与SVRG一样,Prox-SVRG也能达到最优的收敛速率.从随机优化算法的观点来看,SVRG和Prox-SVRG所使用的梯度仍然是整个目标函数梯度的无偏估计,并没有改变随机算法的本质.但是,也正是由于SVRG和Prox-SVRG需要用全梯度来修正单个样本梯度,从而迭代过程中不得不多次遍历所有样本,虽然减小方差的效果明显,但却和批处理算法一样,耗费了大量的计算时间.值得指出的是,SVRG和Prox-SVRG最优收敛速率的获得都依赖于样本数目,从而只能处理样本数目确定的优化问题,并且它们仅限于求解光滑的损失函数问题[8].
对于求解非光滑损失的结构优化问题,COMID算法是一种较好的选择[9].本文主要目的是在COMID中引入方差减小策略,为此,我们首先证明了COMID算法具有方差形式的收敛速率$O(1/\sqrt T + {\sigma ^2}/\sqrt T )$,其中,T是迭代步数,σ2是方差.该收敛速率能够从理论上保证减小方差策略的有效性,进而本文得到一种随机优化算法α-MDVR.为了避免遍历所有样本导致的计算时间多的问题,α-MDVR每次迭代只使用部分样本来修正梯度,既减小了方差,又节省了计算时间,其中,修正梯度需要样本的数目由α决定,也具有较好的柔韧性.另外,对于求解非光滑一般凸优化问题,α-MDVR能够得到最优收敛速率,该收敛速率不依赖于样本数目.对比实验验证了α-MDVR确实能够在适度减小方差的同时节省CPU时间,并获得了比COMID更快的实际收敛速率.
1 光滑损失随机优化算法的减小方差策略为简单起见,本文仅讨论二分类问题.设样本集合:
$S = \left\{ {\left( {{x_1},{y_1}} \right), \ldots ,\left( {{x_n},{y_n}} \right)} \right\} \in {R^n} \times \{ + 1, - 1\} ,$
其中,(xi,yi)是独立同分布的,正则化损失函数的优化问题可以表述为
| $\mathop {min }\limits_{w \in \Omega } \Phi (w),\Phi (w) = r(w) + \frac{1}{n}\sum\limits_{i = 1}^n {{f_i}(w)} $ | (1) |
其中,w∈Rn,r(w)是正则化项,损失函数fi(w)是由样本xi造成的损失.
本节主要介绍SVRG和Prox-SVRG算法,两种算法都是求解光滑强凸优化问题,因此,本节假设损失函数是光滑的,目标函数Φ(w)具有强凸性质.
很多研究者对优化问题(1)的求解进行过研究[1,2,10,11,12,13],其中,梯度下降法是最简单的一阶优化方法,即
| $ {w_t}_{ + 1} = {w_t} - {h_t}g({w_t}) $ | (2) |
其中,g(wt)是关于所有样本目标函数Φ(w)在wt处的全梯度,ηt是学习步长.
随机梯度下降(stochastic gradient descent,简称SGD)[13]是梯度下降法的随机形式.与批处理方法相比,SGD每次迭代中只计算单个样本对应目标函数的梯度,用这种无偏估计避免计算所有样本对应目标函数的梯度. SGD的主要迭代步骤如下:
| $ {w_{t + 1}} = {w_t} - {\eta _t}{\hat g_t}({w_t},{\xi _t}) $ | (3) |
式中,${\hat g_t}({w_t},{\xi _t})$是关于单个样本对应的目标函数在wt处的次梯度,其中,${\{ {x_t}\} _{t> 1}}$表示一系列随机变量,对应的是随机抽取的单个样本.
由于样本是独立同分布的,从而${\hat g_t}({w_t},{\xi _t})$是整个目标函数Φ(wt)次梯度g(wt)的无偏估计,但却存在着方差$E[||{\hat g_t}({w_t},{\xi _t}) - g({w_t})|{|^2}]$,这无疑会影响算法的收敛速率.
Johnson等人提出一种减小方差的方法SVRG[4],其主要迭代步骤如下:
| $ {w_t} = {w_{t - 1}} - \eta (\nabla {\Phi _{{i_t}}}({w_{t - 1}}) - \nabla {\Phi _{{i_t}}}(\tilde w) + \tilde \mu ) $ | (4) |
其中,$\tilde w$是SVRG进行m次迭代后取的平均值,在文献[4]中,m取2n(n为训练样本数);$\nabla {\Phi _{{i_t}}}({w_{t - 1}})$是关于单个样本目标函数在wt-1处的梯度;$\nabla {\Phi _{{i_t}}}(\tilde w)$是关于单个样本目标函数在$\tilde w$处的梯度;$\tilde \mu $是整个目标函数在$\tilde w$处的全梯度,即,$\tilde \mu = \frac{1}{n}\sum\limits_{i = 1}^n {{\Phi _i}} (\tilde w).$
与SGD不同的是,SVRG用$\nabla {\Phi _{{i_t}}}({w_{t - 1}}) - \nabla {\Phi _{{i_t}}}(\tilde w) + \tilde \mu $代替了单个样本的梯度.从形式上看,通过引入修正量,使得方差更小,即,引入修正量后的梯度导致的方差$E[||(\nabla {\Phi _{{i_t}}}({w_{t - 1}}) - \nabla {\Phi _{{i_t}}}(\tilde w) + \tilde \mu ) - g({w_t})|{|^2}]$确实比原有单个样本梯度导致的方差$E[||{\hat g_t}({w_t},{\xi _t}) - g({w_t})|{|^2}]$要小.对于求解光滑损失优化问题,在样本数目确定的情况下,SVRG能够得到指数阶的最优收敛速率.
SVRG是将目标函数Φ(w)看成一个整体来考虑,忽略了损失函数和正则化项有着各自特殊的含义.Xiao等人将问题(1)中的正则化项和损失函数分开考虑,保持正则化项不变,仅对损失项的梯度进行优化.将SVRG由求解简单的黑箱问题推广到具有结构信息的正则化损失函数优化问题,于2014年提出了Prox-SVRG[8].其主要迭代步骤如下:
| $ {w_t} = pro{x_{\eta R}}({w_{t - 1}} - \eta {v_t}),{\rm{ }}{v_t} = (\nabla {f_{{i_t}}}({w_{t - 1}}) - \nabla {f_{{i_t}}}(\tilde w))/({q_{{i_t}}}n) + \tilde v $ | (5) |
其中,$\nabla {f_{{i_t}}}({w_{t - 1}})$是关于单个样本损失函数在wt-1处的梯度;$\nabla {f_{{i_t}}}(\tilde w)$是关于单个样本损失函数在$\tilde w$处的梯度;$\tilde v$是损失函数在$\tilde w$处的全梯度,即,$\tilde v = \frac{1}{n}\sum\limits_{i = 1}^n {{f_i}(\tilde w)} .$
但是,正是由于SVRG和Prox-SVRG需要用全梯度来修正单个样本梯度,从而不得不遍历所有样本,虽然减小方差的效果明显,但却耗费了大量的计算时间.值得指出的是,SVRG和Prox-SVRG最优收敛速率的界都与样本数目有关,从而只能处理样本数目确定的优化问题,并且它们仅限于求解光滑的损失函数问题.
2 非光滑损失问题的α-MDVR算法与问题(1)对应的随机优化问题是:
| $ \mathop {min }\limits_{w \in \Omega } \Phi (w) = r(w) + {E_\xi }[f(w,x)] $ | (6) |
其中,r(w)是正则化项;f(w,x)是损失函数;ξ表示随机变量,对应的是随机抽取的单个样本.
为了方便地进行理论分析和实验验证,本文仅考虑最简单但最典型的非光滑稀疏学习问题“L1正则化+ Hinge损失”,即
$r\left( w \right) = {\left| {\left| w \right|} \right|_1},f\left( {w,x} \right) = max\{ 0,1 - y{{\bf{w}}^T}{\bf{x}}\} .$
与问题(1)不同的是,问题(6)不需要固定样本数,可以描述任意规模的机器学习优化问题.当样本数目充分大时,问题(1)可以看成是问题(6)的一种随机逼近.
对于求解正则化非光滑损失问题(6),如果样本维数足够大,MD(mirror descent)[14]被认为是最优的一阶方法,随机MD的主要迭代步骤如下:
| $ {w_{t + 1}} = \mathop {\arg \min }\limits_{w \in \Omega } \{ {\eta _t}\langle {g_t},w - {w_t}\rangle + {B_\varphi }(w,{w_t})\} $ | (7) |
其中,函数Bφ(w,wt)表示φ函数的Bregman Divergence[15];gt是关于单个样本目标函数Φ(w)在wt处的次梯度;<·,·>表示向量内积.
MD将目标函数Φ(w)当成一个整体进行处理,属于黑箱方法.
2010年,Duchi等人[9]对经典MD算法进行了突破性的改进,将黑箱方法MD扩展到结构方法COMID.该算法在处理优化问题的过程中保持正则化项不动,仅对损失函数进行近似展开,此时的子问题可以解析求解,主要迭代步骤如下:
| $ {w_{t + 1}} = \mathop {\arg \min }\limits_{w \in \Omega } \{ {\eta _t}\langle {g_t},w\rangle + {\eta _t}r(w) + {B_\varphi }(w,{w_t})\} $ | (8) |
与MD不同的是,gt仅为损失函数f(wt,x)在wt处的次梯度.COMID的主要执行过程如算法1所示.
算法 1.
1. Input: initialize w1=0;
2. For t=1 to T
3. Compute gt∈∂f(wt,x)
4. Compute wt+1 via Eq.(8)
5. End for
6. Output: wT or ${\bar w_T} = ({w_1} + ... + {w_T})/T$.
收敛速率是评价随机算法的主要性能指标[16],是数学期望下随机算法输出解对应的目标值向原优化问题最优值收敛的速率,其数学表达式为E[Φ(w)-Φ(w*)],其中,w是随机算法的输出解,w*是原优化问题的最优解. COMID在求解非光滑一般凸优化问题时,有如下定理成立:
定理1[9]. wt是算法(8)第t次迭代的输出.设r(w1)=0,Bφ(w,wt)=||w-wt||2,步长${\eta _t} = {\rm{1 }}/\sqrt t $,且存在常数N,G满足$E[||{w_1} - {w_*}||] \le N,$我们有:
$E\left[ {\Phi \left( {\frac{1}{T}\sum\limits_{t = 1}^T {{w_t}} } \right) - \Phi ({w_*})} \right] \le \frac{{\sqrt T }}{T}({N^2} + {G^2}).$
上述COMID收敛速率的界主要使用损失函数次梯度的上界G进行描述.为了更清楚地了解方差对算法收敛速率的影响,我们需要讨论COMID关于方差描述的收敛速率,具体见下述定理:
定理2. 令wt是算法(8)第t次迭代的输出.假设r(w1)=0,Bφ(w,wt)=||w-wt||2,且存在常数R,M,σ满足$E[||{w_1} - {w_*}||] \le R,E[||\nabla F(w)||] \le M,{E_\xi }[||{g_t}({w_t},\xi ) - \nabla F({w_t})|{|^2}] = \sigma _t^2 \le {\sigma ^2}{\rm{,}}$则
| $ E\left[ {\Phi \left( {\frac{1}{T}\sum\limits_{t = 1}^T {{w_t}} } \right) - \Phi ({w_ * })} \right] \le \frac{{({M^2} + {R^2})}}{{\sqrt T }} + \frac{{{\sigma ^2}}}{{\sqrt T }} $ | (9) |
具体证明见附录.
对于正则化光滑损失函数的凸优化问题,一些常用的结构优化算法具有方差形式描述的最优速率[7].但对于非光滑的一般凸问题,目前仅证明了黑箱形式的MD算法具有方差形式的最优速率[17].定理2实际上证明了结构优化算法COMID也具有方差形式的最优收敛速率.
为了更加清楚地描述每一步迭代导致的方差对算法收敛速率的影响,从定理2的证明过程中还可以得到如下形式的界:
$E\left[ {\Phi \left( {\frac{1}{T}\sum\limits_{t = 1}^T {{w_t}} } \right) - \Phi ({w_*})} \right] \le \frac{{({M^2} + {R^2})}}{{\sqrt T }} + \frac{1}{{2T}}\sum\limits_{t = 1}^T {\frac{1}{{\sqrt t }}} \sigma _t^2.$
从理论分析的角度来说,如果能够在COMID每一步迭代过程中减少σt,显然会有助于提高算法的收敛速率.因此,我们在COMID中引入思路与SVRG和Prox-SVRG类似的减小方差策略,得到一种求解随机优化问题(6)的α-MDVR算法,具体执行流程如下:
算法2. α-MDVR算法.
1. Initialize: ${\tilde w_0} = 0$, w0=0, m=αn
2. Iterate: for s=1,2,...
3. $\tilde w = {\tilde w_{s - 1}}$
4. $\tilde v = \nabla F(\tilde w) = \frac{1}{m}\sum\limits_{t = 1}^m {\nabla {f_t}(\tilde w)} $
5. w0=ws-1
6. Iterate: for t=1,2,…,m
7. Initialize: ${\eta _s} = 1/\sqrt {(s - 1)m + t} $
8. ${g_{t - 1}} = \nabla {f_{t - 1}}({w_{t - 1}},{\xi _{t - 1}}) - \nabla {f_{t - 1}}(\tilde w,{\xi _{t - 1}}) + \tilde v$
9. Compute wt via Eq.(8)
10. end
11. set ${\tilde w_s} = \frac{1}{m}\sum\limits_{t = 1}^m {{w_t}} $
12. set ${w_s} = \frac{1}{{sm}}\sum\limits_{t = 0}^m {{w_t}} $
13. end
算法2中,${g_t}({w_t},{\xi _t}) = \nabla {f_t}({w_t},{\xi _t}) - \nabla {f_t}(\tilde w,{\xi _t}) + \nabla F(\tilde w),\nabla F(\tilde w)$仅仅是关于m个样本损失函数在中间变量$\tilde w$处的梯度,其中,m是算法在一个阶段内迭代的次数.
与SVRG和Prox-SVRG减小方差操作不同的是,α-MDVR在迭代过程中梯度的修正量只取部分样本.值得指出的是,在算法2中,选取部分样本修正后的梯度仍然是样本集合上损失函数梯度的无偏估计,因此,算法2实际上是一种特殊的随机优化算法,定理1仍然适用.但定理2更进一步地解释了方差减少策略的理论依据问题.
为了方便实验和说明修正样本数目对方差及实际收敛速率的影响,α实际上取的是修正梯度所用的样本数目占总样本数目的比例,即,α取定后,修正梯度所用的样本数就是αn,其中,n为所用数据集的样本总数.容易看出,当α=1时,计算$\tilde w$处的梯度需要遍历所有样本,此时,算法减少方差的操作与SVRG和Prox-SVRG完全一致;当α=1/n时,算法不进行梯度修正,即为标准的COMID.综上所述,本文提出的算法从实际运行时间的角度考虑了方差减小问题,α的选取使算法具有更好的柔韧性.
3 实 验本节对随机优化算法α-MDVR的性能进行实验验证.实验所涉及的所有算法均在Sun Fire X4170 M2服务器(2.4GHz Intel(R) Xeon(R)处理器,12G内存,Solaris操作系统)上运行.实验中所用的4个标准数据库均可以从LIBSVM网站中获得,具体下载地址为http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/.表 1给出了4个数据库的详细信息.
| Table 1 Standard database description 表 1 标准数据库描述 |
我们首先在4个标准数据库上验证α-MDVR方差减少策略的有效性;其次验证不同参数α对α-MDVR性能的影响,并同时比较算法的性能.为了公平比较,在实验中所涉及的4个标准数据库上都采取统一的随机方法产生样本,且各算法在4个数据库上均运行10次,将输出结果的平均值作为最终输出.本文实验中所涉及的参数,在一定的范围内,利用网格搜索的方法,选择目标函数下降最快的那一组参数为本文实验所用参数.
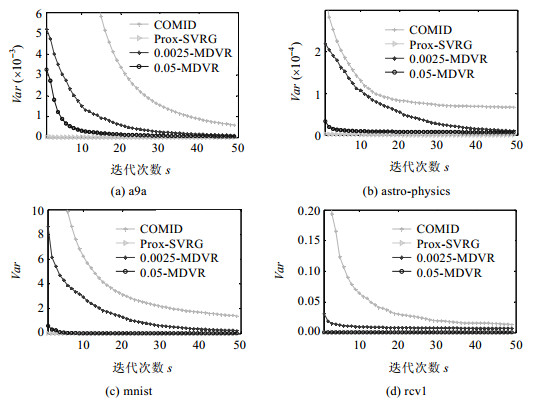
3.1 减小方差验证实验本实验的目的是比较α-MDVR和COMID的实际方差减小效果.图 1为3种算法的方差比较结果图,其中,横坐标表示迭代次数s;纵坐标表示算法的方差(var),即,每次迭代所用的梯度与全梯度之间差值的平方.
|
Fig.1 Variance comparison chart 图 1 方差比较图 |
由图 1中可以看出,α-MDVR方差的减小程度明显都优于COMID,但比使用全部样本修正梯度的方差减小策略要差.即,α取值越大,方差减小的效果越好(实验中,COMID算法的α取值为1/n,其中,n是样本数,Prox-SVRG算法的α取值为1).该实验说明,α-MDVR具有一定的方差减小效果.
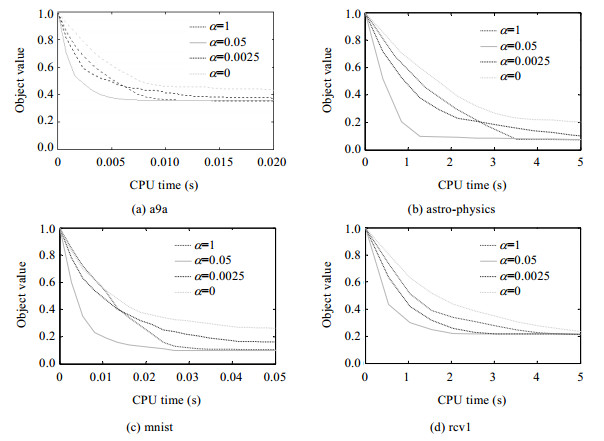
3.2 α对α-MDVR实际性能的影响本实验主要目的是在4个标准数据库上考察不同参数α对α-MDVR算法实际性能的影响.α取不同的值,表示算法在迭代过程中修正梯度时使用了不同的样本数.例如在图 2(c)中,当α=1时,表示修正梯度时需要遍历整个训练集合,即,使用了60 000个样本;当α=0.05时,表示修正梯度时使用了3 000个样本;当α=0.0025时,表示修正梯度时使用了150个样本.为方便起见,我们记α=0时的α-MDVR表示COMID算法,即,不使用任何样本进行梯度修正.
|
Fig.2 When α taking different values, convergence speed comparison chart of α-MDVR 图 2 α取不同值时,α-MDVR的收敛速度比较图 |
图 2为α取不同参数时目标函数收敛情况的比较结果图,其中,横坐标表示CPU时间,纵坐标表示目标函数值(object value).从图中可以看出,当α取合适的值时,α-MDVR的收敛速度比使用全部训练样本修正梯度的算法以及不使用任何样本修正梯度的COMID收敛速度都要快.特别是在上述4个数据库中,当α取0.05时,α-MDVR的性能最佳.
由于随机优化每步迭代所需要的CPU时间基本相同,因此,算法的时间复杂度主要体现在算法达到相同精度所需要的迭代步数上[18, 19],即,收敛速率.从图 2可以看出,α-MDVR算法的收敛速率曲线的下降速度快于COMID算法,这说明α-MDVR算法的时间复杂度更低.
综合第3.1节和第3.2节的实验,虽然α-MDVR方差的减小效果达不到SVRG中使用全部样本时的效果,但当取α取合适的值时,总体计算时间却减少了很多.另一方面,虽然COMID不使用任何样本进行梯度修正,会节省计算时间,但导致的方差仍然会影响实际的收敛速度.总之,对于求解非光滑损失优化问题,α-MDVR在减少方差和缩短运行时间方面具有很好的柔韧性,比COMID具有更快的实际收敛速率.
4 总 结本文针对“L1+Hinge”随机非光滑优化问题.我们首先证明了COMID具有最优的方差形式的收敛速率$O\left( {{\rm{1}}/\sqrt T + {\sigma ^2}{\rm{ }}\sqrt T } \right),$进而在COMID中引入方差减小策略,得到了一种α-MDVR算法,并通过实验验证了α-MDVR能够在适度减小方差的同时节省CPU时间,比COMID具有更快的实际收敛速率.
与文献[9]中COMID的一般性类似,本文提出的算法很容易推广到求解更一般损失函数和正则化项的优化问题,如混合范数的正则化项问题以及矩阵形式的正则化损失函数优化问题等.
附录:定理2的证明证明:将${B_\varphi }\left( {w,{w_t}} \right) = ||w - {w_t}|{|^2}$代入公式(8)中,算法的迭代步骤为
${w_t}_{ + 1} = argmin\{ {\eta _t}\langle {g_t}({w_t},{\xi _t}),w\rangle + {\eta _t}\lambda {\left| {\left| w \right|} \right|_1} + ||w - {w_t}|{|^2}\} .$
令w=w*且$r'\left( {{w_t}} \right) = \partial r\left( {{w_t}} \right)$,有如下的一阶必要条件成立:
| $ {\eta _t}\langle {g_t}({w_t},{\xi _t}) + {\eta _t}r'\left( {{w_t}_{ + 1}} \right) + \nabla \varphi \left( {{w_t}_{ + 1}} \right) - \nabla \varphi \left( {{w_t}} \right),{w_*} - {w_t}\rangle \ge 0 $ | (10) |
根据凸函数的性质,有如下不等式成立:
| $ \begin{array}{l} {\eta _t}[{f_t}({w_t}) - {f_t}({w_ * })] + {\eta _t}[r({w_{t + 1}}) - r({w_ * })] \le {\eta _t}\langle {w_t} - {w_ * },{g_t}({w_t},{\xi _t})\rangle + {\eta _t}\langle {w_{t + 1}} - {w_ * },r'({w_{t + 1}})\rangle \\ {\rm{ }} = {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t})\rangle + {\eta _t}\langle {w_{t + 1}} - {w_ * },{g_t}({w_t},{\xi _t})\rangle + \\ {\rm{ }}{\eta _t}\langle {w_{t + 1}} - {w_ * },r'({w_{t + 1}})\rangle \\ {\rm{ }} = {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t})\rangle - \langle {w_ * } - {w_{t + 1}},{\eta _t}{g_t}({w_t},{\xi _t}) + {\eta _t}r'({w_{t + 1}}) + \\ {\rm{ }}\nabla \varphi ({w_{t + 1}}) - \nabla \varphi ({w_t})\rangle + \langle {w_ * } - {w_{t + 1}},\nabla \varphi ({w_{t + 1}}) - \nabla \varphi ({w_t})\rangle \\ {\rm{ }} \le {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t})\rangle + \langle {w_ * } - {w_{t + 1}},\nabla \varphi ({w_{t + 1}}) - \nabla \varphi ({w_t})\rangle \\ {\rm{ }} = {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t})\rangle + \langle {w_{t + 1}} - {w_ * },{\eta _t}{g_t}({w_t},{\xi _t}) + {\eta _t}r'({w_{t + 1}})\rangle \end{array} $ | (11) |
最后一个不等式可由不等式(10)得到,此时,不等式(11)变为
| $ \begin{array}{l} {\eta _t}[{f_t}({w_t}) - {f_t}({w_ * })] + {\eta _t}[r({w_{t + 1}}) - r({w_ * })] \le {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t})\rangle + \langle {w_ * } - {w_{t + 1}},\nabla \varphi ({w_{t + 1}})\\ - \nabla \varphi ({w_t})\rangle {\rm{ }} = {\eta _t}\langle {w_t} - {w_{t + 1}},{g_t}({w_t},{\xi _t}) - \nabla F({w_t})\rangle + {\eta _t}\langle {w_t} - {w_{t + 1}},\nabla F({w_t})\rangle + \\ {\rm{ }}{B_\varphi }({w_ * } - {w_t}) - {B_\varphi }({w_ * } - {w_{t + 1}}) - {B_\varphi }({w_{t + 1}} - {w_t})\\ {\rm{ }} = {\eta _t}\left\langle {\sqrt {\frac{1}{{{\eta _t}}}} ({w_t} - {w_{t + 1}}),\sqrt {{\eta _t}} ({g_t}({w_t},{\xi _t}) - \nabla F({w_t}))} \right\rangle + \\ {\rm{ }}{\eta _t}\left\langle {\sqrt {\frac{1}{{{\eta _t}}}} ({w_t} - {w_{t + 1}}),\sqrt {{\eta _t}} \nabla F({w_t})} \right\rangle + \\ {\rm{ }}{B_\varphi }({w_ * } - {w_t}) - {B_\varphi }({w_ * } - {w_{t + 1}}) - {B_\varphi }({w_{t + 1}} - {w_t})\\ {\rm{ }} \le {\eta _t}\left( {\frac{{\frac{1}{{{\eta _t}}}||{w_t} - {w_{t + 1}}|{|^2} + {\eta _t}||{g_t}({w_t},{\xi _t}) - FF({w_t})|{|^2}}}{2}} \right) + \\ {\rm{ }}{\eta _t}\left( {\frac{{\frac{1}{{{\eta _t}}}||{w_t} - {w_{t + 1}}|{|^2} + {\eta _t}||\nabla F({w_t})|{|^2}}}{2}} \right) + \\ {\rm{ }}{B_\varphi }({w_ * } - {w_t}) - {B_\varphi }({w_ * } - {w_{t + 1}}) - {B_\varphi }({w_{t + 1}} - {w_t})\\ {\rm{ }} = \frac{1}{2}||{w_t} - {w_{t + 1}}|{|^2} + \frac{{\eta _t^2}}{2}||{g_t}({w_t},{\xi _t}) - \nabla F({w_t})|{|^2} + \frac{1}{2}||{w_t} - {w_{t + 1}}|{|^2} + \\ {\rm{ }}\frac{{\eta _t^2}}{2}||\nabla F({w_t})|{|^2} + ||{w_ * } - {w_t}|{|^2} - ||{w_ * } - {w_{t + 1}}|{|^2} - ||{w_{t + 1}} - {w_t}|{|^2}\\ {\rm{ }} = {B_\varphi }({w_ * } - {w_t}) - {B_\varphi }({w_ * } - {w_{t + 1}}) + \frac{{{\eta _t}^2}}{2}||{g_t}({w_t},{\xi _t}) - \nabla F({w_t})|{|^2} + \\ {\rm{ }}\frac{{\eta _t^2}}{2}||\nabla F({w_t})|{|^2} \end{array} $ | (12) |
第2个不等式可根据$\langle a{{\bf{w}}_1},b{{\bf{w}}_2}\rangle \le {a^2}{\left| {\left| {{w_1}} \right|} \right|^2} + {b^2}{\left| {\left| {{w_2}} \right|} \right|^2}$得到,将公式(12)两边同时除以1/${\eta _t}$,可得:
| $ \begin{array}{l} {f_t}({w_t}) + r({w_t}) - {f_t}({w_*}) - r({w_*}) \le \frac{1}{{{\eta _t}}}{B_\varphi }({w_*},{w_t}) - \frac{1}{{{\eta _t}}}{B_\varphi }({w_*},{w_{t + 1}}) + \frac{{{\eta _t}}}{2}||{g_t}\left( {{w_t},{\xi _t}} \right)\\ - \nabla F({w_t})|{|^2} + {\rm{ }}\frac{{{\eta _t}}}{2}||\nabla F({w_t})|{|^2} + \frac{1}{{{\eta _t}}}[r({w_t}) - r({w_{t + 1}})] \end{array} $ | (13) |
我们假设$E[||\nabla F(w)||] \le M,{E_\xi }[||{g_t}({w_t},\xi ) - \nabla F({w_t})|{|^2}] = \sigma _t^2 \le {\sigma ^2}{\rm{,}}$对不等式(13)两边同时取期望,并从t=1到T求和,得到:
| $ \begin{array}{l} \sum\limits_{t = 1}^T {E[{f_t}({w_t}) + r({w_t}) - {f_t}({w_*}) - r({w_*})]} \le \sum\limits_{t = 1}^T {E\left[ {\frac{1}{{{\eta _t}}}{B_\varphi }({w_*},{w_t}) - \frac{1}{{{\eta _t}}}{B_\varphi }({w_*},{w_{t + 1}})} \right]} + \frac{{{M^2}}}{2}\sum\limits_{t = 1}^T {{\eta _t}} \\ + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}\sigma _t^2} + {\rm{ }}\sum\limits_{t = 1}^T {[r({w_t}) - r({w_{t + 1}})]} \\ {\rm{ }} = \frac{1}{{{\eta _1}}}{B_\varphi }({w_*},{w_1}) + \sum\limits_{t = 2}^T {{B_\varphi }({w_*},{w_t})\left( {\frac{1}{{{\eta _t}}} - \frac{1}{{{\eta _{t - 1}}}}} \right)} - \frac{1}{{{\eta _T}}}{B_\varphi }({w_*},{w_{T + 1}}) + \\ {\rm{ }}\frac{{{M^2}}}{2}\sum\limits_{t = 1}^T {{\eta _t}} + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}} {\sigma _t}^2 + r({w_1}) - r({w_{T + 1}})\\ {\rm{ }} \le \frac{1}{{{\eta _1}}}{B_\varphi }({w_*},{w_1}) + \sum\limits_{t = 2}^T {{B_\varphi }({w_*},{w_t})\left( {\frac{1}{{{\eta _t}}} - \frac{1}{{{\eta _{t - 1}}}}} \right)} + \frac{{{M^2}}}{2}\sum\limits_{t = 1}^T {{\eta _t}} + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}\sigma _t^2} + \\ {\rm{ }}r({w_1}) \end{array} $ | (14) |
取${B_\varphi }\left( {w,{w_t}} \right) = ||w - {w_t}|{|^2},E[||{w_1} - {w_*}||] \le R,r\left( {{w_1}} \right) = 0,{\eta _t} = 1/\sqrt t $因为$\sum\limits_{t = 1}^T {{\eta _t}} = \sum\limits_{t = 1}^T {\frac{1}{{\sqrt t }}} \le 2\sqrt T - 1$,可得:
| $ \begin{array}{l} \sum\limits_{t = 1}^T {E[{f_t}({w_t}) + r({w_t}) - {f_t}({w_*}) - r({w_*})]} \le \frac{1}{{{\eta _1}}}{B_\varphi }({w_*},{w_1}) + \sum\limits_{t = 2}^T {{B_\varphi }({w_*},{w_t})\left( {\frac{1}{{{\eta _t}}} - \frac{1}{{{\eta _{t - 1}}}}} \right)} + \\ {\rm{ }}\frac{{{M^2}}}{2}\sum\limits_{t = 1}^T {{\eta _t}} + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}\sigma _t^2} + r({w_1})\\ {\rm{ }} \le ({M^2} + {R^2})\sqrt T + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}\sigma _t^2} \end{array} $ | (15) |
当我们取固定的方差上界σ,不等式(15)变为
| $ \sum\limits_{t = 1}^T {E[{f_t}({w_t}) + r({w_t}) - {f_t}({w_*}) - r({w_*})]} \le ({M^2} + {R^2})\sqrt T + \frac{1}{2}\sum\limits_{t = 1}^T {{\eta _t}} {\sigma ^2} \le ({M^2} + {R^2})\sqrt T + {\sigma ^2}\sqrt T $ | (16) |
不等式(16)两边同时乘以1/T:
$\frac{1}{T}\sum\limits_{t = 1}^T {E[{f_t}({w_t}) + r({w_t}) - {f_t}({w_*}) - r({w_*})]} = \frac{1}{T}\sum\limits_{t = 1}^T {E[P({w_t}) - P({w_*})]} \le \frac{{({M^2} + {R^2})}}{{\sqrt T }} + \frac{{{\sigma ^2}}}{{\sqrt T }}$.
根据凸函数的性质$\left[ {P\left( {\frac{1}{T}\sum\limits_{t = 1}^T {{w_t}} } \right)} \right] \le \frac{1}{T}\sum\limits_{t = 1}^T {P({w_t})} $,可得到:
$E\left[ {P\left( {\frac{1}{T}\sum\limits_{t = 1}^T {{w_t}} } \right) - P({w_*})} \right] \le \frac{1}{T}\sum\limits_{t = 1}^T {E[P({w_t}) - P({w_*})]} \le \frac{{({M^2} + {R^2})}}{{\sqrt T }} + \frac{{{\sigma ^2}}}{{\sqrt T }}$.
证毕. □
| [1] | Tseng P. Approximation accuracy, gradient methods, and error bound for structured convex optimization. Mathematical Programming, 2010,125(2):263-295 . |
| [2] | Nemirovski A, Juditsky A, Lan G, Shapiro A. Robust stochastic approximation approach to stochastic programming. SIAM Journal on Optimization, 2009,19(4):1574-1609 . |
| [3] | Shalev-Shwartz S, Tewari A. Stochastic methods for L1 regularized loss minimization. In: Proc. of the 26th Annual Int’l Conf. on Machine Learning. 2009. 929-936. |
| [4] | Johnson R, Zhang T. Accelerating stochastic gradient descent using predictive variance reduction. In: Proc. of the Advances in Neural Information Processing Systems 26. 2013. 315-323. |
| [5] | Shalev-Shwartz S, Zhang T. Stochastic dual coordinate ascent methods for regularized loss minimization. arXiv preprint arXiv: 1209.1873, 2012. |
| [6] | Le Roux N, Schmidt M, Bach F. A stochastic gradient method with an exponential convergence rate for strongly convex optimization with finite training sets. arXiv preprint, arXiv: 1202.6258, 2012. |
| [7] | Xiao L. Dual averaging methods for regularized stochastic learning and online optimization. In: Advances in Neural Information Processing Systems. 2009. 2116-2124. |
| [8] | Xiao L, Zhang T. A proximal stochastic gradient method with progressive variance reduction. arXiv: 1403.4699v1, 2014. |
| [9] | Duchi J, Shalev-Shwartz S, Singer Y, Tewari A. Composite objective mirror descent. In: Proc. of the 23rd Annual Workshop on Computational Learning Theory. ACM Press, 2010. 116-128. |
| [10] | Duchi J, Shalev-Shwartz S, Singer Y. Efficient projections onto the L1-ball for learning in high dimensions. In: Proc. of the 25th Int’l Conf. on Machine Learning. 2008. 272-279. |
| [11] | Beck A, Teboulle M. A fast iterative shrinkage thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2009,2(1):183-202 . |
| [12] | Nesterov Y. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Mathematics Doklady, 1983,27(2):372-376. |
| [13] | Bottou L. Stochastic Gradient Descent Tricks. Neural Networks: Tricks of the Trade. Berlin, Heidelberg: Springer-Verlag, 2012. 421-436 . |
| [14] | Beck A, Teboulle M. Mirror descent and nonlinear projected subgradient methods for convex optimization. Operations Research Letters, 2003,31(3):167-175. |
| [15] | Bregman LM. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Computational Mathematics and Mathematical Physics, 1967,7(3):200-217. |
| [16] | Hazan E, Kale S. Beyond the regret minimization barrier: An optimal algorithm for stochastic strongly convex optimization. Journal of Machine Learning Research, 2014,15(1):2489-2512. |
| [17] | Lan G. An optimal method for stochastic composite optimization. Mathematical Programming, Series A, 2012,133(1-2):365-397 . |
| [18] | Shalev-Shwartz S, Singer Y, Srebro N. Pegasos: Primal estimated sub-gradient solver for SVM. Mathematical Programming, 2011, 127(1):3-30 . |
| [19] | Lin QH, Chen X, Peña J. A sparsity preserving stochastic gradient method for composite optimization. Manuscript, Carnegie Mellon University, 2011. 15213. |
 2015, Vol. 26
2015, Vol. 26


