2.中国科学技术大学 计算机科学与技术学院, 安徽 合肥 230027;
3.中国科学院 信息工程研究所 信息安全国家重点实验室, 北京 100093
2.School of Computer Science and Technology, University of Science and Technology of China, Hefei 230027, China;
3.State Key Laboratory of Information Security, Institute of Information Engineering, The Chinese Academy of Sciences, Beijing 100093, China
自从Gentry[1]设计第一个全同态加密方案以来,全同态加密方案研究立即成立当前密码学研究热点[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19].因为全同态加密技术允许对加密数据实行任意计算,所以全同态加密技术能够用于解决云计算中用户数据安全和隐私保护问题.然而,现有全同态加密方案存在密文膨胀率大、密文同态计算复杂性高、方案安全性假设较强等问题,结果导致现有方案在云计算环境中不具有实用性.因此,如何设计实现安全、有效的全同态加密方案,目前仍然是一个公开问题.
1.1 相关研究Gentry[1]基于理想格问题的全同态加密方案主要组成3个关键步骤:Gentry首先设计支持有限密文乘法和加法的有点同态加密方案,因为每个密文中都存在噪声,并且每次密文同态运算增加新产生密文的噪声,当密文中噪声达到一定阈值时,新产生的密文就不能正确解密,这就限制了有点同态加密方案仅能够计算有界低度的密文多项式;其次,Gentry压扁解密算法,以便它能被表示为密文和密钥比特的低度多项式;最后,Gentry引入自举性关键思想,不仅能在密文和密钥比特上计算这个解密多项式,而且能够在那些密钥比特的密文上实行同态计算,产生原密文中明文的一个新密文.
如果解密多项式的度数足够小,则新密文中的噪声能够变得比原密文中的噪声更小,以便这个新密文能够再次进行同态加法或乘法运算.使用这种密文刷新算法后,有点同态加密方案允许同态密文运算的次数变成无限,从而获得了全同态加密方案.
目前,设计全同态加密方案主要有3种类型.
(1) 基于理想格的全同态加密方案和实现
为了实现Gentry方案,Smart和Vercauteren[3]基于主理想格优化设计了全同态加密方案.这种主理想格能够使用两个整数来表示,而且该方案私钥仅为一个整数.Smart和Vercauteren能够实现基本的有点同态加密方案,但他们的方案并不能支持足够大参数条件下的Gentry压扁解密技术.因此,他们并没有真正实现全同态加密方案.主要困难在于Smart和Vercauteren方案的密钥生成算法复杂性太高.因为他们的方案需要产生行列式为素数的主理想格,而且即使发现这种主理想格后,计算其私钥的复杂性至少也得是$\tilde{\Theta }({{n}^{2.5}}),$n为格的维数.结果导致他们不能产生维数n>2028的密钥.而且,Smart和Vercauteren估计压扁解密多项式的度数将达到几百,故为获得全同态加密方案,需要理想格的维数至少为n=227.因此,目前Smart和Vercauteren方案在实际中无法有效产生密钥.
Gentry和Halevi[7]第一次真正实现了Gentry全同态加密方案.Gentry和Halevi的方案也是基于主理想格,但仅要求主理想格的行列式为奇数,并不要求其一定是素数.在实现方案时,Gentry和Halevi使用了许多优化方法,包括在文献[3, 17]中建议的方法.对于其方案的最安全环境(即72bit安全),公钥大小约为2.3GB,在高端工作站上一次密文刷新需要用时30分钟,密文膨胀率约为n=O(223).
针对文献[3, 7]中的方案,Gu和Gu[20]给出了求解小倍数私钥的格归约攻击方法.根据文献[21]中计算分析的LLL算法[22]的平均性能,当n≤8192时,他们的方案并不是安全的,而且文献[20]中也给出了直接恢复明文的格归约攻击方法.使用该攻击方法,我们在中国科技大学超级计算中心的单个处理机上用时22天成功恢复出维数n=256时密文中的明文.
针对文献[3]中的方案,Hu和Wang[23]通过构造修改的私钥、修改的解密算法和特定密文空间子集,给出了新的攻击方法.若密文来自这个特定子集,则该方法使用修改私钥和解密算法能够正确解密.
(2) 基于整数上近似GCD问题的全同态加密方案和实现
2010年,Dijk,Gentry,Halevi和Vaikuntanathan(DGHV)[2]构造了基于整数上近似GCD问题的全同态加密方案.与Gentry方案相比,这个方案的优点在于概念上的简单性,因为它仅在整数上进行计算操作.方案简单性的代价是其公钥大小达到$\tilde{O}({{\lambda }^{10}})$(l为安全参数),以致于对任何实际系统来说其公钥都太大.
代替文献[2]中的方案,使用公钥整数的线性函数加密,Coron,Mandal,Naccache和Tibouchi[4]使用公钥整数的二次函数进行加密,将公钥大小从$\tilde{O}({{\lambda }^{10}})$减少到$\tilde{O}({{\lambda }^{7}})$使用文献[7]中的优化技术,文献[4]中的方案获得了相似的性能,即,公钥大小为802MB和一次密文刷新需要用时14分钟.因此,文献[4]真正实现了文献[2]中的全同态加密方案,其方案安全性基于近似GCD问题的更强变种,即,部分近似GCD问题.为了进一步减少文献[2]中方案的公钥大小,Coron,Naccache和Tibouchi[5]使用基于Hash函数的压缩技术,将方案公钥大小从$\tilde{O}({{\lambda }^{7}})$减少到$\tilde{O}({{\lambda }^{5}})$此时,方案语义安全性仍然基于部分近似GCD问题难度,但已控制在随机神谕安全模型下.文献[5]中的方案将公钥由802MB减少到10.1MB,一次密文刷新需要时间为11分34秒,密文膨胀率为$\tilde{O}({{\lambda }^{5}})$而且,Coron,Naccache和Tibouchi[5]还扩展文献[11]中的模切换技术到整数近似GCD上,从而构造了无引导的层次DGHV型全同态加密方案.为了降低密文膨胀率,类似于文献[3]中的批密文技术,Coron,Lepoint和Tibouchi[6]构造了基于中国剩余定理的批全同态加密方案.
针对文献[4]中的方案,Chen和Nguyen[24]设计了基于单变量多点计算方法的新PAGCD求解算法,其时间和空间为穷举搜索数的平方根,即$\tilde{O}({{2}^{\lambda /2}}),$因而从实验上破解了文献[4]中的方案.而且,Chen和Nguyen直接使用PAGCD算法给出了求解AGCD算法,其时间为$\tilde{O}({{2}^{3\lambda /2}}),$空间为$\tilde{O}({{2}^{\lambda /2}}).$使用与文献[22]同样的方法,Coron,Naccache和Tibouchi[5]给出了运行时间和空间都为$\tilde{O}({{2}^{\lambda }})$的启发式求解AGCD算法.
(3) 基于LWE(Ring-LWE)问题的全同态加密方案和实现
Brakerski和Vaikuntanathan在文献[9, 10]中分别构造了基于Ring-LWE和LWE问题的全同态加密方案.为了降低密文膨胀率和密文同态计算复杂性,Brakerski和Vaikuntanathan引入了新的维数约减技术和模切换技术.理论上,文献[9, 10]中的全同态方案公钥大小仅为O(n3+2εlogO(1)n)比特,密文大小为O(n1+ε),但上述参数中隐含的常数因子非常大.实际上,Lauter,Naehrig和Vaikuntanathan[25]实现了文献[9]中基于Ring-LWE的有点同态加密方案,但并未实现全同态加密方案.根据文献[25],当Ring-LWE的维数n=4096、最大密文度数D=15时,公钥大小约为60MB;当n=16384、最大密文度数D=15时,公钥大小约为2 946MB.
最近,Brakerski,Gentry和Vaikuntanathan[11]基于文献[9, 10]中的模切换技术设计了无引导的层次同态加密方案,其安全性基于求解伪多项式因子nO(logn)的Ring-LWE问题难度.假定Ring-LWE的维数为n,噪声大小为n,则理论上该方案的公钥大小约为O(n3logO(1)n).在这种新的全同态加密方案框架中,通过模切换技术将每次密文乘法时新密文中噪声增长由原来的二次增长降为线性增长,代价是每次密文同态计算后模按比例阶梯减少.因而,这种新框架有可能真正提高实际全同态加密方案的性能.
为了改进在Ring-LWE上全同态加密方案的性能,Gentry,Halevi和Smart[12]基于特殊数模(如形为整数2k+1)设计了更好的引导技术,在某些情况下,甚至允许“私钥”加密为一个密文,从而减少公钥大小.在文献[13]中,Gentry,Halevi和Smart使用批密文技术进行密文同态计算,计算t门的宽度Ω(λ)的电路需要时间为tlogO(1)λ.为了将全同态加密方案应用于实际中,文献[14]使用许多优化方法实现了在全同态加密方案上计算高级加密标准算法AES-128电路.使用NTL库[26],文献[14]中实现的一个变种方案,花费36小时对整个AES运算过程进行同态密文计算;运用SIMD(single-instruction multiple-data)技术,使得每次同态密文计算处理54块明文,获得每块明文的同态密文计算补偿时间约为40分钟;再进一步加以改进,使得每次同态密文计算能够处理720块明文,获得每块明文的同态密文计算补偿时间约为5分钟.
在2012年,Brakerski[15]基于新的张量技术构造了基于LWE的全同态加密方案,并归约其安全性到格的近似因子为nO(logn)的经典GapSVP问题的最坏情况求解难度,n为格的维数.然而,该方案的密文同态计算复杂性也很大,不具有实用性.最近,Brakerski和Vaikuntanathan[18]证明了分层全同态加密方案的安全性在量子计算上归约到近似因子为O(n1.5+ε)(或在经典计算上归约到近似因子为O(n2+ε))的GapSVP问题求解难度.Gentry,Sahai和Waters[19]基于近似特征向量法构造了全同态加密方案,其安全性归约到LWE假设.GSW方案的优点在于,概念上更易于理解,理论上渐近性能更好,密文同态加法和乘法计算仅是矩阵加法和乘法.但实际上,其性能要比目前最好的基于RLWE的方案[11, 12, 13, 14, 15]还差一个对数因子(logn)O(1).Lopez-Alt[16]构造了基于NTRU 型的多密钥全同态加密方案,该方案能够用于云环境下实时多方安全计算.
Gu和Wu[27]使用文献[10]中的密文乘法技术设计了基于近似格问题的全同态加密方案,由于方案中私钥向量的极大范数为较小(通常为常数或安全参数的线性函数),为使方案安全,格的维数n需要足够大,公钥大小约为O(n3logO(1)n),密文膨胀率也很大.
另外,Gentry和Halevi[8]构造了新的全同态加密方案,它是有点同态方案和乘法同态加密方案(如Elgamal方案)的一种混合方案.这个方案使用判定Diffie-Hellman难度假设替换了Gentry方案中的稀疏子集和难度问题(sparse subset sum problem,简称SSSP)假设,去除了Gentry方案中的压扁解密电路步骤.
国内相关研究:据我们所知,目前国内全同态加密方案的研究成果甚少[23],相关研究主要是基于(全)同态加密方案构造新的密码原语[28, 29, 30, 31].胡予濮和王凤和[23]提出了针对基于主理想格的全同态加密方案[3]的特定攻击方法.张永、温涛、郭权和李凤坤[28]通过引入全同态加密方案提出了一种对偶密钥建立方案;陈嘉勇、王超、张卫明和祝跃飞[29]采用修正全同态加密算法设计了载密图像加密算法;孙中伟、冯登国和武传坤[30]提出了基于加同态公钥密码算法的匿名数字指纹方案;光炎等人[31]基于LWE构造了无证书全同态加密方案.另一方面,针对云计算环境中隐私保护和密文检索等安全问题[32, 33],国内密码学者也进行了深入的研究和探索[34, 35, 36].然而,这些研究着重于解决云计算安全中的某一特定函数密文计算,并不能实行任意函数的全同态密文计算.
通过分析上述全同态加密方案,可以发现:
· 第1种全同态加密方案是基于理想格构造.为保证方案安全性,理想格的维数不能太小,目前在文献[1, 3, 7, 17]中给出的方案维数至少为1 024以上;为了能够实现密文同态计算,理想格基的范数必须足够大;
· 第2种全同态加密方案是基于整数上近似GCD问题.然而为了避免格归约攻击,公钥中每个xi的比特长度至少为l5以上(l为安全参数),否则方案就不安全[2, 24];
· 第3种全同态加密方案基于LWE/Ring-LWE问题[37, 38],该问题本身可以看作格中CVP问题.为了保证方案的安全性,LWE/Ring-LWE的维数也比较大.为了实行密文同态计算,在基于LWE/Ring-LWE的方案中要求模p足够大,密文中噪声很小.然而,方案安全性反比于模p与噪声的比,即:如果模p与密文中噪声的比越大,则越易受到格归约算法的攻击,方案安全性越低.根据当前优化实现的全同态加密方案性能来看,基于Ring-LWE的方案效率最高[39, 40, 41].
另一方面,近年来格归约算法的研究不断取得进展[21, 22, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51],特别是求解最小格向量的随机筛算法.所以,为了保证方案的安全性,基于格/理想格问题的全同态加密方案的维数必须足够大.
因此,在上述全同态加密方案中,每种方案各有其优缺点.问题是能否设计新的全同态加密方案,继承上述方案中的优点而摒除它们的缺点.这是本文的研究主题.
1.2 本文结果本文研究的主要结果是设计实现基于多项式环上近似理想格问题的全同态加密方案,并归约证明方案安全性到部分近似理想格问题.DGHV方案[2]在概念上非常简单,然而为了避免格归约攻击,方案公钥元素必须设置得非常大.本文所提方案通过扩展近似GCD问题到多项式环上近似理想格问题方法来避免格归约攻击.
本质上,本文方案类似于文献[52]中使用理想格时的公钥加密方案,这一点与文献[2]中的方案类似于文献[53]中的公钥加密方案一样.实际上,Ajtai和Dwork[52]构造了基于多维格的扰动格点的公钥加密方案,而Regev[53]构造了基于一维格的扰动格点的公钥加密方案,它们的安全性都基于唯一最短向量问题求解难度.与文献[2]中的方案一样,本文方案公钥的格点扰动程度比文献[52]中方案公钥的格点扰动程度更小,导致文献[52]中最坏情况到平均情况的安全归约似乎也不能应用于本文方案.
本文重新分析稀疏子集和问题求解难度,以减少公钥大小并提高同态计算效率.在文献[7, 17]中,稀疏子集和问题都假定敌手知道稀疏子集的和.实际上,在全同态加密方案中,这个和是隐藏的.在这种情况下,隐藏稀疏子集和问题并不适用存在生日攻击问题.
1.3 本文结构本文第2节描述相关预备知识.第3节构造基于部分近似理想格的有点同态加密方案.第4节归约证明有点同态加密方案安全性到部分近似理想格问题,并讨论已知攻击.第5节设计基于部分近似理想格的全同态加密方案.第6节构造批全同态加密方案.第7节设计基于近似理想格的全同态加密方案.第8节实现全同态加密方案,并与已有方案的性能进行比较.第9节总结全文,并讨论构造扩展和公开问题.
2 预备知识 2.1 符号约定设ρ为安全参数,k为2的幂,k=O(logρ),n为正整数.集合[n]={1,…,n}.<x>表示最接近x的整数.同理,记<v>为向量(或多项式)v中每个分量(或系数)的最接近整数的向量(或多项式).设Z为整数集,R为整数多项式环R=Z[x]/<xk+1>,Rn=R/nR.如果定义R在实数上,则记为${{R}_{\mathbb{R}}}.$设δ为正整数,${{R}_{\mathbb{R},\delta }}=\{y\in {{R}_{\mathbb{R}}}|{{2}^{\delta }}y\in R\}$,即,${{R}_{\mathbb{R},\delta }}$为${{R}_{\mathbb{R}}}$中系数的小数位至多δ比特的元素集.对于?u∈R,设||u||∞为u系数向量极大范数.对于R,其膨胀因子γmul为n,即: ||uxv||∞≤k×||u||∞×||v||∞. 这里,×是R中乘法.
设r←ψS表示根据分布ψ从集合S中选取元素r.A≡cB表示对任意多项式时间算法分布A,B是计算上不可区分的.
2.2 理想格和近似GCD问题给定m个线性无关向量b1,b2,…,bm∈Zn,格是bi所有整数线性组合的集合%$L({{b}_{1}},{{b}_{2}},...,{{b}_{m}})=\{\sum\nolimits_{i=1}^{m}{{{x}_{i}}{{b}_{i}},{{x}_{i}}\in Z}\}.$我们也使用矩阵B∈Znxm表示向量bi.如果B为L的一个基,则B支撑格L.对于任何格L的基B,定义:
P(B)={Bx|x∈$\mathbb{R}$m,?i:-1/2≤xi<1/2}.
当m=n时,设det(B)表示B的行列式.
设$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}={{({{u}_{0}},{{u}_{1}},...,{{u}_{n-1}})}^{T}}$为u∈R的系数向量,定义$rot(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u})={{(-{{u}_{n-1}},{{u}_{0}},...,{{u}_{n-2}})}^{T}},$矩阵:
$Rot(u)=(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u},rot(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}),...,ro{{t}^{n-1}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u})).$
称Rot(u)为理想格(u)的基.理想I?R称为主理想,如果它能由一个元素生成.
因参数较多,本文假设$\lambda =\tilde{O}({{\rho }^{2}}),\eta =\tilde{O}({{\rho }^{2}}),\tau =\tilde{O}({{\rho }^{2}})$和$\gamma =\tilde{O}({{\rho }^{5}}).$在本文方案实现时,给出各个参数选取的具体值.
设p是比特长度为λ的奇数,定义在Z上比特长度为g的整数分布DZ,γ,ρ(p):
DZ,γ,ρ(p)={b=qp+r|q←UZ∩[0,2γ/p),r←UZ∩(-2ρ,2ρ)}.
定义2.1(近似GCD问题,AGCD).给定DZ,γ,ρ(p)的一列随机抽样{bi=qip+ri,i∈[τ]},求p.
定义2.2(部分近似GCD问题,PAGCD).给定DZ,γ,ρ(p)的一列随机抽样{bi=qip+ri,i∈[τ]}和b0=q0p,求p.
设多项式h∈R满足||h||∞=2λ和h mod 2=1,定义在R上多项式分布DR,ρ,γ,η(h):
DR,ρ,γ,η(h)={f=g×h+e|g,e∈R,||g||∞∈[2η],||e||∞∈[2ρ]}.
定义2.3(近似理想格问题,AILP).给定DR,ρ,γ,η(h)的一列随机抽样{fi=gih+ei,i∈[τ]},求h.
定义2.4(部分AILP的问题,PAILP).给定DR,ρ,γ,η(h)的一列随机抽样{fi=gixh+ei,i∈[τ]}和f0=g0h,求h.
变种PAILP1.设q0=O(2kh),p=det(Rot(h))为素数.给定DR,ρ,γ,η(h)的一列随机抽样{fi=gixh+ei,i∈[τ]}和f0=q0p,求h.
变种PAILP2.设pi=det(Rot(hi)),i=1,2为素数,h=h1h2.给定DR,ρ,γ,η(h)的一列随机抽样{fi=gixh+ei,i∈[τ]}和f0=p1p2,求h.
评论2.1.当k=1时,近似理想格问题变成近似GCD问题,PAILP变成PAGCD.
评论2.2.条件h mod 2=1仅是为了使全同态加密方案的解密算法简单,在安全归约证明时并不需要这个条件.
评论2.3.在PAILP1中,要求q0,p为素数是为了使整数f0=q0p难以分解.因为gcd(h,xk+1)=(x-α) mod p,即:在模p下,h,xk+1有公因式x-α.如果对手已知p(如分解f0=q0p),则在有限域Fp上可以有效分解xk+1,并进而通过格归约算法求解h.但对于合数f0,目前还没有有效算法[54]分解xk+1,也得不到公因式x-α.因此在PAILP1中,要求f0=q0p为两个大素数之积.
评论2.4.在PAILP1中,因为p=p(h-1xh)=(ph-1)xh,即,f0=q0p=(q0ph-1)xh对应于PAGCD中无噪声元素b0=q0p.这里,h-1是h在实数上的逆,ph-1是整数上多项式.因此,变种PAILP1是PAILP的一种特殊情况.另一方面,在PAILP中,敌手能够计算${{{f}'}_{0}}=\det (Rot({{f}_{0}}))=\det (Rot({{g}_{0}}))\det (Rot(h))={{q}_{0}}p,$即,转换PAILP到PAILP1.从评论3可知:在PAILP中要求f0′难以分解,否则易于通过分解f0′来求解h.
评论2.5.在PAILP2中,f0=p1p2=(f0h-1)xh,f0h-1是整数上多项式,而且也要求f0=p1p2难以分解.否则,当敌手分解f0后,则首先分解${{x}^{k}}+1=\prod\nolimits_{j\in [k]}{(x-{{\alpha }_{i,j}})}\bmod {{p}_{i}}$;然后,利用中国剩余定理计算${{\beta }_{{{j}_{1}},{{j}_{2}}}}$满足:
$\left\{ \begin{array}{*{35}{l}} {{\beta }_{{{j}_{1}},{{j}_{2}}}}={{\alpha }_{i,{{j}_{1}}}}\bmod {{p}_{1}} \\ {{\beta }_{{{j}_{1}},{{j}_{2}}}}={{\alpha }_{i,{{j}_{2}}}}\bmod {{p}_{2}} \\ \end{array} \right.,{{j}_{1}},{{j}_{2}}\in [k];$
最后,由gcd(h,xk+1)=(x-α) mod f0可知:在由两个元素$(p,{{\beta }_{{{j}_{1}},{{j}_{2}}}})$生成的k2个理想格中,有一个与理想格h相同.又因为k较小,LLL算法一般能够获得理想格$(p,{{\beta }_{{{j}_{1}},{{j}_{2}}}})$的最小生成基.因此,在k2个格归约基中有一个与h相同.
评论2.6.本质上,PAILP1和PAILP2与PAILP相同,基于它们设计的全同态加密方案都依赖于大整数分解难度.然而,基于PAILP1方案的密文膨胀率最大(约为k2(λ+η)),基于PAILP2方案的密文膨胀率次之(约为k2λ),基于PAILP方案的密文膨胀率最小(约为k(λ+η)).但PAILP除了提供f0=g0h外,还给定了${{{f}'}_{0}}=\det (Rot({{f}_{0}}))={{q}_{0}}p,$即,PAILP提供给敌手的信息最多.然而目前并不知道在不分解${{{f}'}_{0}}$的情况下,如何利用f0求解PAILP.
2.3 对称多项式(symmetric polynomial)根据文献[55]中的引理4,给定比特向量ω=(ω1,ω2,…,ωt),其海明权重二进制表示的第i比特等于第2i初等对称多项式${{e}_{{{2}^{i}}}}(\omega )\bmod 2,$即,${{e}_{{{2}^{i}}}}(\omega )\bmod 2=(\sum\nolimits_{|S|={{2}^{i}},S\subset [t]}{\prod\nolimits_{j\in S}{{{\omega }_{j}}}})\bmod \text{ }2.$而且,我们能够计算在w上初等对称多项式作为多项式${{P}_{\omega }}(x)=\prod\nolimits_{j=1}^{t}{(x-{{\omega }_{j}})}$中形式变量x的系数,如${{e}_{{{2}^{i}}}}(\omega )\bmod 2$为${{x}^{t-{{2}^{i}}}}$的系数.
计算初等对称多项式的动态规划算法[2].
输入:比特向量ω=(ω1,ω2,…,ωt);输出:向量ω的分量和${{P}_{1,t}},{{P}_{2,t}},{{P}_{4,t}},...,{{P}_{{{2}^{i}},t}}.$
(1) 初始化:设P0,k=1,k=0,1,…,t-1和Pj,0=0,j=1,2,…,2i //Pj,k为在ω1,…,ωk上的第j个对称多项式
(2) For k=1 to t //每次循环加入ωk,计算产生ω1,…,ωk组成的对称多项式
(3) For j=2i downto 1
(4) Pj,k=ωkxPj-1,k-1+Pj,k-1
(5) 输出${{P}_{1,t}},{{P}_{2,t}},{{P}_{4,t}},...,{{P}_{{{2}^{i}},t}}.$
2.4 剩余Hash引理(leftover Hash lemma)从有限集X到有限集Y的Hash函数族H是两两独立的(pairwise independent),如果对于所有不同的x,x',${{\Pr }_{h{{\leftarrow }_{R}}H}}[h(x)=h({x}')]=1/|Y|.$分布D是ε-均匀的(ε-uniform),如果它与均匀分布的统计距离至多为ε.这里,有限集X上分布D1,D2的统计距离是$\frac{1}{2}\sum\nolimits_{x\in X}{|{{D}_{1}}(x)-{{D}_{2}}(x)|}.$
定义2.5.从X到Y的Hash函数族H是ε-两两独立的,如果:
$\sum\nolimits_{x\ne {x}'}{({{\Pr }_{h{{\leftarrow }_{R}}H}}[h(x)=h({x}')]-1/|Y|)}\le \frac{|X{{|}^{2}}}{|Y|}\varepsilon .$
引理2.1(leftover Hash lemma[56]).设H是从X到Y两两独立的Hash函数族.假定h←UH和x←UX是独立
均匀选择的,则(h,h(x))是HxY上$\frac{1}{2}\sqrt{|Y|/|X|}$-均匀的.
引理2.2(leftover Hash lemma[4]).设H是从X到Y的ε-两两独立Hash函数族.假定h←UH和x←UX是独
立均匀选择的,则(h,h(x))是HxY上$\frac{1}{2}\sqrt{|Y|/|X|+\varepsilon }$-均匀的.
2.5 全同态加密下面基于文献[57]自适应地回顾全同态加密方案及其语义安全性的定义.
定义2.6(同态公钥加密方案HE).HE是由4个概率多项式时间算法(HE.KeyGen,HE.Enc,HE.Dec,HE.Eval)组成的.
· HE.KeyGen(1ρ)是概率多项式时间算法,输入为安全参数1ρ,输出为公钥pk和私钥sk;
· HE.Enc(pk,m)是概率多项式时间算法,输入为公钥pk和明文比特m,输出密文c;
· HE.Dec(sk,c)是多项式时间算法,输入为私钥sk和密文c,输入明文比特m;
· HE.Eval(pk,C,c1,c2,...,cn)是多项式时间算法,输入为公钥pk,电路C,n个密文c1,c2,...,cn,输出密文c.这里,电路C输入n个比特,输出1bit.
实际上,任意电路计算都可以转化为由加法门和乘法门组成的电路计算.因此,本文在设计同态加密方案时仅考虑加法门和乘法门同态计算.
定义2.7(电路保密性(circuit-privacy)和简洁性(compactness)).电路保密性是指由同态加密中算法HE.Eval计算产生的密文不显示超出电路输出本身的电路任何其他内容,即使知道私钥;简洁性是指HE.Eval输出密文长度至多为安全参数ρ的多项式p(ρ)大小.
定义2.8(C-同态).设C={Cn}n∈N为一类布尔电路,这里,Cn指的是输入n个比特,输出1个比特的电路集.同态方案HE是C-同态,如果对于足够大安全参数ρ,每个多项式n(ρ),每个电路E∈Cn和每个输出比特序列m1,m2,...,mn:
$$\begin{align}
& \Pr [(pk,sk)\leftarrow HE.KeyGen({{1}^{\rho }}); \\
& \quad \ {{c}_{i}}\leftarrow HE.Enc(pk,{{m}_{i}}),i\in [n]; \\
& \quad \ c\leftarrow HE.Eval(pk,E,{{c}_{1}},{{c}_{2}},...,{{c}_{n}}); \\
& \quad \ HE.Dec(sk,c)\ne E({{m}_{1}},...,{{m}_{n}})]=negl(\rho ).\\
\end{align}$$
这里,概率是在HE.KeyGen,HE.Enc随机选择之上.
定义2.9(全同态加密FHE).方案HE是全同态加密方案,如果它对于GF(2)上所有算术电路类是同态的.
定义2.10(IND-CPA安全).方案HE是IND-CPA安全的,如果对任意概率多项式时间敌手A:
$$\begin{align} & |\Pr [(pk,sk)\leftarrow HE.KeyGen({{1}^{\rho }}):A(pk,HE.Enc(pk,0))=1]- \\ & \ \Pr [(pk,sk)\leftarrow HE.KeyGen({{1}^{\rho }}):A(pk,HE.Enc(pk,1))=1]|=negl(\rho ).\\ \end{align}$$
3 有点同态加密方案(SHE)跟随Gentry[1]构造全同态加密方案的框架,我们首先构造基于PAILP的有点同态加密方案SHE;然后,通过使用Gentry引导技术转换SHE方案到全同态加密方案FHE.
3.1 SHE 构造密钥生成算法. SHE.KeyGen.
(1) 随机选择多项式g0,h∈R满足q0=det(Rot(g0)),p=det(Rot(h))为素数,且h mod 2=1和||h||∞=2λ,||g0||∞ ∈[2η],计算f0=g0h∈R;
(2) 随机选择两组多项式gt,j,et,j∈R,t∈[2],j∈[τ]满足||gi,j||∞∈[2η],||ei,j||∞∈[2ρ],计算ft,j=hgt,j+et,j;
(3) 输出公钥pk=(k,f0,{ft,j}t∈[2],j∈[t])和私钥sk=(h).
加密算法.SHE.Enc.
给定公钥pk和消息比特m∈{0,1},随机选择ri,j∈R,i,j∈[τ]和r∈R满足||ri,j||∞∈[2ρ]和||r||∞∈[2ρ].输出密文:
$$c=(m+2r+2\sum{{{r}_{i,j}}{{f}_{1,i}}}{{f}_{2,j}})\bmod {{f}_{0}}.$$
密文加算法.SHE.Add.
给定公钥pk和密文c1,c2,计算输出密文c=(c1+c2) mod f0.
密文乘算法.SHE.Mul.
给定公钥pk和密文c1,c2,计算输出密文c=(c1×c2) mod f0.
解密算法.SHE.Dec.
给定私钥sk和密文c,计算输出m=[<c×h-1> mod x]2⊕[c mod x]2.这里,h-1是在${{R}_{\mathbb{R}}}$上h的逆.
上述算法中,c mod f0是指计算c mod Rot(f0),即,将c对应的向量$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}$映射到以Rot(f0)为格基的平行四边形(parallelization)内部.
3.2 SHE正确性因为要求q0=det(Rot(g0)),p=det(Rot(h))为素数,故算法SHE.KeyGen的时间主要用于产生满足条件的g0,h.尽管对于很大的k(如k>1024),目前不易产生满足条件的g0,h,但对于实用的k(如k≤1024,见文献[3]),则易于通过随机方法产生满足条件的g0,h.
如果k=2,则可以利用当p=1 mod 4时p=a2+b2的性质,在概率多项式时间内产生素数${{p}_{i}}=a_{i}^{2}+b_{i}^{2}$满足pi=1 mod 4,分别取h=a1+b1x,g0=a2+b2x.易于验证p=p1,q0=p2.
引理3.1. 算法SHE.Enc,SHE.Add,SHE.Mul输出密文c都具有形式c=gxh+2e+m.
证明:由SHE.Enc易得$c=(m+2r+2\sum{{{r}_{i,j}}{{f}_{2,i}}{{f}_{2,j}}})\bmod {{f}_{0}}=g\times h+2e+m.$
由SHE.Add可知,给定密文ci=gih+2ei+mi,i=1,2,则:
c=(c1+c2) mod p=(g1+g2)h+2(e1+e2)+(m1+m2) mod f0.
由SHE.Mul可知,给定密文ci=gih+2ei+mi,i=1,2,则:
c=(c1×c2) mod f0=(g1g2h+g2(2e1+m1)+g1(2e2+m2))h+2(2e1e2+e1m2+e2m1)+m1m2 mod f0.
证毕.
引理3.2.如果密文c中噪声多项式的极大范数小于 2λ/(2k)
2λ/(2k) ,则SHE.Dec是正确的.
,则SHE.Dec是正确的.
证明:给定密文c和私钥sk,由引理3.1可知,c具有形式c=gxh+2e+m.解密计算如下:
[ c×h-1+0.5I
c×h-1+0.5I mod x]2⊕[c mod x]2=[
mod x]2⊕[c mod x]2=[ (gxh+2e+m)xh-1+0.5I
(gxh+2e+m)xh-1+0.5I mod x]2⊕[(gxh+2e+m) mod x]2 =[
mod x]2⊕[(gxh+2e+m) mod x]2 =[ g+(2e+m)xh-1+0.5I
g+(2e+m)xh-1+0.5I mod x]2⊕[(g+m) mod x]2 =[g mod x]2⊕[(g+m)mod x]2 =[g mod x]2⊕[g mod x]2⊕[m]2=m.
mod x]2⊕[(g+m) mod x]2 =[g mod x]2⊕[(g+m)mod x]2 =[g mod x]2⊕[g mod x]2⊕[m]2=m.
因为||2e||∞< 2λ/(2k)
2λ/(2k) ,所以||(2e+m)xh-1||∞≤2λ/(2k)x||h-1||1<1/2.
,所以||(2e+m)xh-1||∞≤2λ/(2k)x||h-1||1<1/2.
引理3.3.如果密文中噪声多项式的极大范数小于2ρ',则SHE能够正确计算由这些密文组成的电路深度为$d\le \log \frac{\lambda -\log 2k}{{\rho }'+\log k}$的任意加法和乘法门电路C.
证明:假定密文ci=gih+2ei+mi,i=1,2.为了正确解密,由引理3.2可知,算术电路输出密文的噪声多项式的极大范数 2λ/(2k)
2λ/(2k) .加法门的噪声多项式的极大范数呈线性增长,而乘法门的极大范数呈指数增长.因此,乘法运算控制了密文算术电路深度.
.加法门的噪声多项式的极大范数呈线性增长,而乘法门的极大范数呈指数增长.因此,乘法运算控制了密文算术电路深度.
设c=(c1×c2) mod f0=gh+2e+m1m2 mod f0,这里,g=(g1g2h+g2(2e1+m1)+g1(2e2+m2)) mod f0,e=(2e1e2+e1m2+e2m1),则有:
||2e||∞=||(2e1+m1)x(2e2+m2)||∞≤k||2e1+m1||∞||2e2+m2||∞≤22r'+logk<22(r'+logk).
因此,d必须满足不等式${{2}^{{{2}^{d}}({\rho }'}}^{+\log k)}<{{2}^{\lambda }}/(2k),$即$d\le \log \frac{\lambda -\log (2k)}{{\rho }'+\log k}.$
3.3 SHE性能公钥pk=(k,f0,{ft,j}t∈[2],j∈[t])的比特大小为$\tilde{O}(k{{\rho }^{4}}),$私钥sk=(h)的比特大小为$\tilde{O}(k{{\rho }^{2}}),$密文的膨胀率为$\tilde{O}(k{{\rho }^{2}}),$加密算法时间主要为$\tilde{O}({{\tau }^{2}})$次乘法.为了减少加密时间在实现时一般选择$\tilde{O}(\rho )$非0的元素ri,j.在这种情况下,加密时间压缩为$\tilde{O}(\rho )$次乘法.解密算法时间为1次乘法.注意,当维数k越小时,为保证安全,$\eta =\tilde{O}({{\rho }^{2}})$中隐含的对数因子需要取得越大.
4 SHE的安全性我们首先在第4.1节给出SHE方案的安全性归约证明.然后,在第4.2节描述针对SHE方案已知攻击的安全分析.注意:第4.2节和第5.4节的安全分析并不是严格的安全证明,仅是分析方案能够避免目前已知攻击算法.
本节归约第3节SHE方案的安全性到求解部分近似理想格问题难度.实际上,部分近似理想格问题扩展了部分近似GCD问题.Dijk,Gentry,Halevi和Vaikuntanathan在文献[2]的变种和优化部分已经提出设计基于部分近似GCD的方案,文献[4, 5]使用部分近似GCD问题优化实现了文献[2]的全同态加密方案.
本节安全性归约证明主要自适应文献[2]中安全性归约证明方法.文献[2]的主要归约思路是通过使用攻击SHE的算法A构造求解近似GCD问题的算法B,包括4个步聚:(1) 根据近似GCD问题产生SHE方案公钥;(2) 使用A构造求解p的近似倍数的最小比特位算法;(3) 利用步骤(2)中的算法构造求解p的近似倍数的Binary GCD算法;(4) 直接恢复近似GCD p.
在自适应上述安全归约的过程中,困难主要来自于第3步,即,并不能使用Binary GCD算法求解近似理想格问题的近似倍数.因为文献[2]中Binary GCD能够使整数近似GCD的近似倍数不断减少(每次约减少1/2),而在近似理想格问题上无法实现Binary GCD算法.然而,我们能够自适应归约证明基于部分近似理想格问题的安全性,这也是构造基于PAILP的SHE的原因之一.
本文的安全归约方法与文献[2]中方法的不同之处在于:文献[2]中的Binary GCD算法针对近似GCD中的近似倍数,而本文的Binary GCD算法则针对近似理想格中的噪声多项式.本文安全归约方法也适用于基于部分近似GCD的SHE方案.
4.1 安全性归约引理4.1.给定n=det(Rot(f))为奇数的f∈R,则在模f下2的逆元2-1=(n+1)/2.
证明:因为n=det(Rot(f)),故n=(nf-1)xf,且nf-1是整数上多项式,所以2x(n+1)/2=(n+1) mod f =1 mod f,即:
2-1=(n+1)/2 mod f.
证毕.
例4.1:设f=125+16x+4x2+2x3,e=2+6x-4x2+4x3,则
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}={{(2\text{ }6\text{ }-4\text{ }4)}^{T}}$,n=det(Rot(f))=246202433,2-1=(n+1)/2=123101217.
所以,
$\begin{align} & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}_{1}}={{2}^{-1}}\times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}={{(246202434\text{ }738607302\text{ }-492404868\text{ }492404868)}^{T}},\\ & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}_{2}}=\langle Rot{{(f)}^{-1}}\times {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}_{1}}\rangle ={{(2463163\text{ }5656947\text{ }-4673078\text{ }4316960)}^{T}},\\ & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}_{1}}-Rot(f)\times \langle Rot{{(f)}^{-1}}\times {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}}}_{1}}\rangle ={{(1\text{ }3\text{ }-2\text{ }2)}^{T}}.\\ \end{align}$
故2-1e mod f=1+3x-2x2+2x3.
所以,当多项式e的系数都是偶数时,在模f下乘以2-1等价于e除以2.
定理4.1.任意具有优势e的SHE攻击算法A都能够转换为求解分布为DR,ρ,γ,η(h)的近似理想格问题算法B,成功概率为ε/2.B的运行时间是tA,r和1/e的多项式,tA为 A的运行时间.
证明:我们从算法A构造求解近似理想格问题算法B.算法B从分布DR,ρ,γ,η(h)中获取需要的独立抽样数,目的是求解h.
在证明中,我们假定每次调用算法A,其返回形如c=(gxh+r) mod p中噪声r的常系数奇偶比特,无论r的其他系数的奇偶性.实际上,这个假设与SHE中解密算法的返回结果一致.
评论4.1.如果密文c=(gxh+r)中r为其他形式时,算法A返回随机结果(或特殊符号⊥),则本节归约证明仅对k=O(logρ)成立.因为在这种情况下,只有2k=ρO(1)个可能值,敌手能够猜测r mod 2的值,每次猜测后调用A.如果猜测正确,则在多项式次调用中返回正确结果的概率具有绝对优势;否则,返回结果中0和1的概率基本相等(或特殊符号⊥).
步骤1.产生公钥.
B从分布DR,ρ,γ,η(h)中抽取2t个抽样ft,j,t∈[2],j∈[τ]和f0=g0h,输出公钥pk=(k,f0,{ft ,j}t∈[2],j∈[t]).
步骤2.计算噪声多项式系数奇偶性子程序.
给定h的一列近似倍数,B使用A获得关于h的这些近似倍数中噪声多项式系数的奇偶性,即,调用子程序Learn-Noise-Coeff-Parity.
Learn-Noise-Coeff-Parity(v,pk)
给定v=(gxh+e) mod n满足||e||∞≤2ρ,计算e mod 2.
(1) For t=0 to k-1 do //依次求解噪声多项式的第t项系数的奇偶性
(2) wt=(xk-tv) mod (xk+1) //将噪声多项式的第t项系数移到常数项位置
(3) For s=1 to poly(ρ)/ε do
(4) 随机选择比特${{m}_{i}}\in \{0,1\},r_{i,j}^{s}\in R,i,j\in [\tau],r_{0}^{s}\in R$,满足$||r_{i,j}^{s}|{{|}_{\infty }}={{2}^{\rho }},||r_{0}^{s}|{{|}_{\infty }}={{2}^{\rho }}.$
(5) 计算${{c}_{i}}=({{w}_{t}}+{{m}_{i}}+2r_{0}^{s}+2\sum\nolimits_{i,j\in [\tau]}{r_{i,j}^{s}{{f}_{1,i}}{{f}_{2,j}}})\bmod {{f}_{0}},$
(6) 调用A得到bi=A(pk,ci)⊕mi,
(7) 设置ut等于bi中出现次数最多的值.
(8) 输出$u=\sum\nolimits_{t=0}^{k}{{{u}_{t}}{{x}^{t}}}$作为e mod 2.
步骤3.去除h的近似倍数中噪声多项式.
当由步骤2获得噪声多项式系数的奇偶性神谕(oracle)时,去除h的近似倍数中噪声多项式就比较容易.
给定v=(gxh+e) mod f0,输出v'=(2ρ+logρgxh) mod f0=g'xh.
(1) For i=0 to ρ+logρ do
(2) u=Learn-Noise-Coeff-Parity(v,pk)
(3) v=v-u
(4) v=(2-1xv) mod f0 //注意:当n=det(Rot(f0))为奇数时,模f0下,2-1=(n+1)/2
(5) u=Learn-Noise-Coeff-Parity(v,pk)
(6) v'=v+u //为了去除噪声多项式中系数为‘-1’的项.如果v'=0,步骤3重新开始.
评论4.2.因为v=(g×h+e) mod f0中噪声e满足条件||e||∞≤2ρ,但e的系数有正有负:如果某个系数ei为正,则ei-ui为正偶数,且2-1(ei-ui) mod f0将ei-ui减少1/2,程序一直循环,直到该系数为0;如果某个系数ei为负,则ei-ui为负偶数,且2-1(ei-ui) mod f0将ei-ui在绝对值上减少1/2,但这个系数不可能减至0,因为当ei=-1时,ui=1,则ei-ui=-2和2-1(ei-ui) mod f0=-1,即,当ei减少到-1后,每次循环后仍然为-1.故步骤3中第(6)小步使用加u以去除噪声中所有系数为‘-1’的项.
步骤4.计算GCD.
使用GCD算法求解p=gcd(det(Rot(v')),det(Rot(f0)))和gcd(f0,xk+1)=(x-α) mod p.
步骤5.求解h.
因为两个元素(p,α)生成的理想格与h生成的理想格相同,故由(p,α)构造格L,然后调用LLL格归约算法得到最短向量作为多项式h的系数向量:
$$L=\left( \begin{matrix} p & 0 & 0 & \cdots & 0 \\ -\alpha & 1 & 0 & \cdots & 0 \\ -{{\alpha }^{2}} & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ -{{\alpha }^{k-1}} & 0 & 0 & \cdots & 1 \\ \end{matrix} \right).$$
评论4.3.因为本文中维数k一般较小(通常为O(logρ)或常数),故步骤5中通过LLL格归约算法一般能够直接得到h.另一方面,若k较大(如为rO(1)),则可通过LLL格归约算法尝试求解h或h的倍数h'=s×h.若||h'||∞/||h||∞较小且det(Rot(h'))=p,则可直接使用h'的逆(h')-1去解密密文;否则,构造格${L}'=\left( \begin{matrix} Rot({v}') \\ Rot({h}') \\ \end{matrix} \right)=\left( \begin{matrix} Rot(h)Rot({g}') \\ Rot(h)Rot(s) \\ \end{matrix} \right),$并调用LLL格归约算法求解Rot(h)或Rot(h)U,U为单模矩阵,这里假定g',s互素.当然,在k较大时,使用LLL格归约算法求解h不一定成功.
上述步骤4和步骤5也可以由步骤4-5'替换.
步骤4-5'.求解h.
构造格$L=\left( \begin{matrix} Rot({v}') \\ Rot({{f}_{0}}) \\ \end{matrix} \right)=\left( \begin{matrix} Rot(h)Rot({g}') \\ Rot(h)Rot({{g}_{0}}) \\ \end{matrix} \right)$,并调用LLL格归约算法求解Rot(h)或Rot(h)U,U为单模矩阵.由于
本文中k较小,故LLL算法一般能够得到h.
B的成功概率分析:
首先,由步骤1可知,B产生的公钥分布与SHE方案中的公钥分布相同;
其次,步骤2中的子程序Learn-Noise-Coeff-Parity(v,pk)是e mod 2的可靠神谕.由引理4.1可知:除了公钥的可忽略部分外,对于所有公钥,程序Learn-Noise-Coeff-Parity第(5)行产生的密文ci的分布是统计上接近于SHE方案中比特(e mod x mod 2)⊕mi的密文分布.使用计数方法易于证明:如果在公钥pk下敌手A具有猜测加密比特优势e,那么对于私钥集中至少ε/2的私钥h,敌手A具有优势至少ε/2;而且在与这部分私钥h对应的公钥集中,至少e/4部分的公钥,敌手A具有优势至少e/4.因此,Learn-Noise-Coeff-Parity的第(6)行敌手A具有优势至少e/4-negl,并且Learn-Noise-Coeff-Parity(v,pk)的多数选举策略将以具压倒性优势的概率返回正确答案.所以,步骤3将去除h的近似倍数中噪声多项式,获得h的倍数;
最后,算法B的步骤4和步骤5将恢复h.因此,对于A具有优势至少ε/2的h,公钥集中至少e/4-negl部分,A具有优势至少e/4.对于A具有优势至少ε/2的h,使用新随机公钥4/exw(logρ)次重复调用算法B,以压倒性优势的概率恢复h.因此,算法B的成功概率至少为ε/2.
证毕.
引理4.2.给定参数(ρ,λ,η,τ),设sk=h,pk=(k,f0,{ft,j}t∈[2],j∈[t])是SHE.KeyGen随机产生的.对每个满足||e||∞≤2ρ的f*=(gxh+e) mod f0,设分布:
${{D}_{pk}}({{f}^{*}})=\{{{c}^{*}}=({{f}^{*}}+2{{r}_{0}}+2\sum\nolimits_{j\in [\tau]}{{{r}_{i,j}}{{f}_{1,i}}{{f}_{2,j}}})\bmod {{f}_{0}}\ \ |\ \ {{r}_{i,j}}\in R,||{{r}_{i,j}}|{{|}_{\infty }}\le {{2}^{\rho }},i,j\in [\tau]\ \}.$
那么在sk,pk选择上以压倒性优势的概率,每个分布Dpk( f*)在统计上接近于分布:
SHE.Enc(pk,m=e mod x mod 2).
证明:引理4.2的证明与文献[4]中引理D.1的证明相同,仅由引理4.3替换文献[4]中的引理4.2.
设g∈R,Rg={y mod g|y∈R}是以Rot(g)为格基的平行四边形内部元素,Rρ={y∈R|||y||∞∈[2ρ]}.设H是从$R_{\rho }^{\tau \times \tau }$到Rg的Hash函数簇,成员w∈H关联到Rg中的元素gt,j,t∈[2],j∈[τ].对于$r\in R_{\rho }^{\tau \times \tau },$定义:
$w(r)=\sum\nolimits_{i,j\in [\tau]}{{{r}_{i,j}}{{g}_{1,i}}{{g}_{2,j}}}\bmod g.$
证毕.
引理4.3.设g∈R,q=det(Rot(g))为素数,Hash函数簇H是ε两两独立的.这里,$\varepsilon \approx \frac{1}{q}+\frac{{{\tau }^{2}}}{{{2}^{k\rho {{\tau }^{2}}-2(k\rho +1)\tau }}}.$
证明:由引理2.2,引理4.3的证明与文献[4]中引理4.2的证明相同,除了文献[4]在Zq上计算,而这里在Rg上计算.符号对应关系:在公式ε中,这里的q指的是Rg中的元素个数,文献[4]中指的是Zq中的元素个数;这里的kρ对应于文献[4]中的α.
评论4.4.上述针对变种PAILP的安全归约证明可以直接应用于PAILP1和PAILP2问题,仅在算法中将$\frac{1}{2}=(\det (Rot({{f}_{0}}))+1)/2$替换为$\frac{1}{2}=({{f}_{0}}+1)/2,$其他证明相同.
4.2 已知攻击由于PAILP扩展自PAGCD问题,故针对PAGCD的攻击方法[2, 58]都需要考虑其攻击PAILP的可行性.本节主要研究分析对SHE方案的已知攻击和如何设置方案参数以避免这些攻击.
4.2.1 因式分解攻击因为在SHE的pk中包含f0=g0h,敌手能够计算{{{f}'}_{0}}=\det (Rot({{f}_{0}}))={{q}_{0}}p.{{{f}'}_{0}}中最小素因子约为kη比特,使用Lenstra的椭圆曲线因子分解算法[52]需要时间约为$\exp (O(\sqrt{k\eta }))\approx \exp (O(\sqrt{k}\rho )),$仍为ρ的指数时间.
4.2.2 连分数攻击[58]如果直接计算${{{f}'}_{i}}=\det (Rot({{f}_{i}}))={{q}_{i}}p+{{e}_{i}},$易于验证:通常情况下,ei≈(qip)(k-1)/k>>p.不失一般性,假定ei mod p均匀分布,则${{e}_{i}}\bmod p <<\sqrt{p}$的概率几乎为0.故,通过两个元素$({{{f}'}_{0}},{{{f}'}_{i}})$的连分数计算得到p的概率几乎为0.
下面首先通过例子扩展整数上连分数概念到多项式环R上的连分数.
例4.2:设y0=125+16x+4x2+2x3,y1=2+6x-4x2+4x3.在R上使用欧几里德算法计算:
$\begin{align} & {{y}_{0}}={{q}_{0}}(x){{y}_{1}}+{{y}_{2}}=(13-2x-3{{x}^{2}}-18{{x}^{3}}){{y}_{1}}+(-5+2x+2{{x}^{2}}-4{{x}^{3}}); \\ & {{y}_{1}}={{q}_{1}}(x){{y}_{2}}+{{y}_{3}}=(-1-2x-2{{x}^{2}}-2{{x}^{3}}){{y}_{2}}+(-3+2x+0{{x}^{2}}-2{{x}^{3}}); \\ & {{y}_{2}}={{q}_{2}}(x){{y}_{3}}=(3+0x-2{{x}^{2}}-2{{x}^{3}}){{y}_{3}}.\\ \end{align}$
在上述算法中,${{q}_{i}}(x)=\langle {{y}_{i}}y_{i+1}^{-1}\rangle $,简记为qi.易于验证det(Rot(y3))=1.
定义y0/y1连分数为$\frac{{{y}_{0}}}{{{y}_{1}}}={{q}_{0}}+\frac{1}{{{q}_{1}}+\frac{1}{{{q}_{2}}}}.$
为了使对任意一对(y0,y1),y1≠0,上述扩展连分数定义有意义,需证明:如果yi+1≠0,则在${{R}_{\mathbb{R}}}$中存在$y_{i+1}^{-1}.$因为如果Rot(yi+1)可逆,即det(Rot(yi+1))≠0,则$y_{i+1}^{-1}.$存在.又因为当k为2的幂时,f=xk+1为Z上不可约多项式,故gcd(f,yi+1)=1.由文献[54]中的推论6.15可知,f,yi+1的结式(resultant)S的行列式det(S)≠0.通过简单矩阵变换,可得det(Rot(yi+1))=det(S).所以,当yi+1≠0时,det(Rot(yi+1))≠0,即,yi+1在${{R}_{\mathbb{R}}}$中可逆.
现在考虑公钥元素(f0,fi)形成的连分数.因为${{\left\| \frac{{{f}_{i}}}{{{f}_{0}}}-\frac{{{g}_{i}}}{{{g}_{0}}} \right\|}_{\infty }}={{\left\| \frac{{{r}_{i}}}{{{g}_{0}}h} \right\|}_{\infty }},$所以期望$\frac{{{g}_{i}}}{{{g}_{0}}}$出现在多项式环的连分数中.
实际上,仅有$\frac{{{f}_{i}}}{{{f}_{0}}}$接近$\frac{{{g}_{i}}}{{{g}_{0}}}$并不意味着连分数的输出需要近似值$\frac{{{g}_{i}}}{{{g}_{0}}}$因此,当||ri||∞较大时,连分数法攻击不会成功.
4.2.3 格归约攻击因为近似GCD问题中求解的p具有原子性,而在近似理想格问题中求解的h具有更多组合性,导致文献[2]中的方案易于受到格归约的攻击,而基于近似理想格的方案更难以通过格归约进行攻击.
(1) 通过公钥求解私钥h的格归约攻击
如果由(f0,f1,1)构造格${{L}_{1}}=\left( \begin{matrix}
Rot({{f}_{1,1}}) & {{I}_{k}} \\
Rot({{f}_{0}}) & 0 \\
\end{matrix} \right),$则det(L1)=q0p.由Minkowsky定理[59]可知,L1的最短长度向量 满足条件||v||∞≤(q0p)1/(2k)≈2(λ+η)/2.另一方面,L1包含向量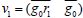 满足条件||v1||∞≈2η+ρ.因此,当λ<<η时,L1中包含有指数多个向量v,其长度小于||v1||∞,即,格归约并不能产生关于向量v1的有用信息.
满足条件||v1||∞≈2η+ρ.因此,当λ<<η时,L1中包含有指数多个向量v,其长度小于||v1||∞,即,格归约并不能产生关于向量v1的有用信息.
如果由(f1,i,f1,j)构造格${L_2} = \left( {\begin{array}{*{20}{c}} {Rot({f_{1,i}})}&{{I_k}} \\ {Rot({f_{1,j}})}&0 \end{array}} \right),$则det(L2)=det(Rot(f1,j))≈2k(λ+η),与格L1的情况相似.
易于验证:如果由t(t>2)个公钥元素构造格,其包含的最小向量长度与上述由2个元素构造格的情况类似.
(2) 通过公钥和密文求解明文的格归约攻击
给定公钥pk=(k,f0,{ft,j}t∈[2],j∈[t])和密文c,构造格L3:
${L_3} = \left( {\begin{array}{*{20}{c}} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c} }&0& \cdots &0&0& \cdots &0&1 \\ {Rot(2{f_{1,1}}{f_{2,1}}\bmod {f_0})}&0& \cdots &0&0& \cdots &{{I_k}}&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} &0& \vdots \\ {Rot(2{f_{1,1}}{f_{2,\tau }}\bmod {f_0})}&0& \cdots &0&{{I_k}}& \cdots &0&0 \\ {Rot(2{f_{1,2}}{f_{2,1}}\bmod {f_0})}&0& \cdots &{{I_k}}&0& \cdots &0&0 \\ \vdots & \vdots & {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} &0& \vdots & \vdots & \vdots & \vdots \\ {Rot(2{f_{1,\tau }}{f_{2,\tau }}\bmod {f_0})}&{{I_k}}& \cdots &0&0& \cdots &0&0 \\ {Rot({f_0})}&0& \cdots &0&0& \cdots &0&0 \end{array}} \right).$
因为det(L3)=q0p,由Minkowsky定理可知,L3的最短长度向量v满足条件:
$||v|{{|}_{\infty }}\le {{({{q}_{0}}p)}^{1/(({{\tau }^{2}}+1)k+1)}}\approx {{2}^{(\lambda +\eta )/({{\tau }^{2}}+1)}}={{2}^{O(1)}}.$
而由密文$c = (m + 2r + 2\sum {{r_{i,j}}{f_{1,i}}{f_{2,j}}} )\bmod {f_0}$可知${{v}_{c}}=(2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}+\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {m},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}_{1,1}},...,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}_{1,\tau }},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}_{\tau ,1}},...,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}_{\tau ,\tau }},1)\in {{L}_{3}}$,满足||vc||∞=||ri,j||∞=O(2ρ).因此,如果格归约算法能够求得较短长度的向量v1,则v1与向量vc之间关系能够获得明文信息.然而,为了获得2τ近似因子的向量,现有格归约算法需要时间约为O(2τ),显然,在计算上是不可行的.
4.2.4 枚举攻击最简单的枚举攻击猜测公钥中噪声多项式.因为ft,j=hgt,j+et,j,则可以猜测et,j.这种蛮力攻击的时间复杂性为O(2kρ).
最近,Chen和Nguyen[24]给出了求解PAGCD的算法.如果x0=pq0和xi=pqi+ri,这里,0≤ri<2ρ,1≤i≤τ,则$p=\gcd \left( {{x}_{0}},\prod\limits_{j=0}^{{{2}^{\rho }}-1}{({{x}_{1}}-j)}\bmod {{x}_{0}} \right).$因为${{f}_{t}}(x)=\prod\limits_{i=0}^{t-1}{({{x}_{1}}-(x+i))}\bmod {{x}_{0}},$所以$\prod\limits_{j=0}^{{{2}^{\rho }}-1}{({{x}_{1}}-j)}=\prod\limits_{j=0}^{{{2}^{{\rho }'+(\rho \bmod 2)}}-1}{{{f}_{{{2}^{{{\rho }'}}}}}({{2}^{{{\rho }'}}}j)}\bmod {{x}_{0}},$记
ρ'= ρ/2
ρ/2 .因此,求解PAGCD需要使用一次GCD、2ρ'+(ρmod 2)-1次模乘法和计算2ρ'度的多项式的2ρ'+(ρmod 2)点值,这个计算费用至多为$\tilde{O}({{2}^{{{\rho }'}}})=\tilde{O}({{2}^{\rho /2}}).$
.因此,求解PAGCD需要使用一次GCD、2ρ'+(ρmod 2)-1次模乘法和计算2ρ'度的多项式的2ρ'+(ρmod 2)点值,这个计算费用至多为$\tilde{O}({{2}^{{{\rho }'}}})=\tilde{O}({{2}^{\rho /2}}).$
然而在自适应PAGCD算法求解近似理想格问题时,并不能获得同样的性能.
尽管$h=\gcd (\prod\nolimits_{||r|{{|}_{\infty }}\le {{2}^{\rho }}}{({{f}_{1,1}}-r)}\bmod {{f}_{0}},{{f}_{0}}),$但在模f0下,定义多项式系数为关于变量r0,ρ1,…,rk/2-1的d=(2ρ+1+1)k/2度的多元多项式:
${{b}_{d}}({{r}_{0}},{{r}_{1}},...,{{r}_{k/2-1}})=\prod\limits_{{{r}_{k-1}}=-{{2}^{\rho }}}^{{{2}^{\rho }}}{...\prod\limits_{{{r}_{k/2}}=-{{2}^{\rho }}}^{{{2}^{\rho }}}{({{f}_{1,1}}-{{r}_{k-1}}{{x}^{k-1}}-...-{{r}_{k/2}}{{x}^{k/2}}-{{r}_{k/2-1}}{{x}^{k/2-1}}-{{r}_{0}})}}\bmod {{f}_{0}}.$
易于看出,多元多项式${{b}_{{{2}^{k\rho /2}}}}({{r}_{0}},{{r}_{1}},...,{{r}_{k/2-1}})$的展开式中项数至少为2kρ.故,通过这种方法并不能减少计算$\prod\nolimits_{||r|{{|}_{\infty }}\le {{2}^{\rho }}}{({{f}_{1,1}}-r)}\bmod {{f}_{0}}$的时间.
易于看出:当1<i<k时,蛮力猜测r的k-i个系数会产生度为d=(2ρ+1+1)(k-i)的i元多项式需要计算,其计算时间复杂性并不比穷举算法时间O(2kρ)更少.
然而,当蛮力猜测r的k-1个系数,产生度为d=(2ρ+1+1)(k-1)的单变量多项式:
$${{b}_{d}}({{r}_{0}})=\prod\limits_{{{r}_{k-1}}=-{{2}^{\rho }}}^{{{2}^{\rho }}}{...\prod\limits_{{{r}_{1}}=-{{2}^{\rho }}}^{{{2}^{\rho }}}{({{f}_{1,1}}-{{r}_{k-1}}{{x}^{k-1}}-...-{{r}_{k/2}}{{x}^{k/2}}-{{r}_{1}}{{x}^{1}}-{{r}_{0}})}}\bmod {{f}_{0}}$$ 时,则这种蛮力攻击计算时间复杂性为O(2(k-1)ρ),比完全穷举攻击稍好一点,但代价是需要空间为O(2(k-1)ρ). 5 全同态加密方案(FHE)因为SHE的解密算法所需要的布尔电路深度比有点同态加密方案能够处理的电路深度更深,因此我们使用Gentry压扁解密算法从SHE构造全同态加密方案.Gentry压扁解密算法的目的是使SHE的解密算法能够表示成由SHE同态运算支持的低度多项式,并且最终应用引导变换实现全同态加密方案.关键是构造SHE方案,使其能同态计算的多项式度数超过解密多项式度数的两倍.这种SHE方案称为可引导的,并且能够被转化为全同态加密方案.
5.1 压扁解密电路因为解密时仅需计算<c×h-1>,所以为正确解密h-1中的每个系数,保留精度至δ=λ+η+O(logρ)比特位.
使用Gentry引导技术,在公钥中添加一个稀疏子集$S=\{{{y}_{i}}\in {{R}_{\mathbb{R},\delta }}:i\in [\Theta]\},$私钥为对应于集合S的比特特征向量ω=(ω1,…,ωΘ),满足ω的Hamming权重θ<<Θ,并且$||(\sum\nolimits_{i=1}^{\Theta }{{{\omega }_{i}}{{y}_{i}}}\bmod 2)-{{h}^{-1}}|{{|}_{\infty }}\le {{2}^{-\delta -1}}.$
给定一个密文c∈R,解密算法可以修改为 $$\begin{align} & Dec(c,S,\omega )={{[\langle c\times {{h}^{-1}}\rangle \bmod x]}_{2}}\oplus {{[c\bmod x]}_{2}} \\ & \quad \quad \quad \quad \quad ={{[\langle c\times \sum\nolimits_{i=1}^{\Theta }{{{\omega }_{i}}{{y}_{i}}}\rangle \bmod x]}_{2}}\oplus {{[c\bmod x]}_{2}} \\ & \quad \quad \quad \quad \quad ={{[\langle \sum\nolimits_{i=1}^{\Theta }{{{\omega }_{i}}(c\times {{y}_{i}})}\rangle \bmod x]}_{2}}\oplus {{[c\bmod x]}_{2}} \\ & \quad \quad \quad \quad \quad ={{[\langle \sum\nolimits_{i=1}^{\Theta }{{{\omega }_{i}}{{u}_{i}}}\rangle \bmod x]}_{2}}\oplus {{[c\bmod x]}_{2}} \\ & \quad \quad \quad \quad \quad ={{[\langle \sum\nolimits_{i=1}^{\Theta }{{{\omega }_{i}}{{u}_{i}}\bmod x}\rangle]}_{2}}\oplus {{[c\bmod x]}_{2}}.\\ \end{align}$$ 这里,ui=cxyi.
为提高效率,与文献[7, 17]一样,我们将Θ个元素分成θ个小块,每块中包含Θ/θ个元素,满足在比特特征向量ω=(ω1,…,ωΘ)中对应于每个小块中有且仅有一个ωi=1,其余都为0.
5.2 FHE构造在密文同态计算过程中,密文中的噪声一直在增长.当密文中的噪声达到某一阈值时,就不能再实行密文同态计算,否则,新产生的密文就不是明文比特的正确密文.在这种情况下,需要使用密文刷新算法(recrypt).Recrypt能够将高噪声密文c转化为低噪声密文cnew,并且密文cnew与c加密的明文比特相同.为了方案可引导,在FHE方案公钥中,需要提供私钥比特向量w的密文.因此,与现有全同态加密方案一样,我们也假定FHE是KDM[60]安全的.
FHE密钥生成算法. FHE.KeyGen.
(1) 使用SHE.KeyGen产生pk=(k,f0,{ft,j}t∈[2],j∈[t])和sk=(h);
(2) 计算产生${{h}^{-1}}\in {{R}_{\mathbb{R},\delta }};$
(3) 随机选择θ个子集${{S}_{i}}=\{{{y}_{i,j}}\in {{R}_{\mathbb{R},\delta }},j\in [\Theta /\theta]\},$子集Si的比特特征向量ωi=(ωi,1,…,ωi,Θ/θ)满足有且仅有一个ωi,j=1,其余都为0,并且$\sum\nolimits_{i=1}^{\theta }{\sum\nolimits_{j=1}^{\Theta /\theta }{{{\omega }_{i,j}}{{y}_{i,j}}}}={{h}^{-1}}\bmod 2;$
(4) 加密ωi,j作为${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\omega }}_{i,j}}={{a}_{i,j}}\times h+2{{e}_{i,j}}+{{\omega }_{i,j}}$满足||ai,j||∞∈[2η],||2ei,j||∞∈[2ρ];
(5) 输出公钥$PK=(k,{{f}_{0}},{{\{{{f}_{t,j}}\}}_{t\in [2],j\in [\tau ]}},{{\{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\omega }}_{i,j}},{{y}_{i,j}}\}}_{i\in [\theta ],j\in [\Theta /\theta ]}})$和私钥SK=(ω1,…,ωq).
加密算法.FHE.Enc.
与SHE.Enc相同.
密文加算法.FHE.Add.
与SHE.Add相同.
密文乘算法.FHE.Mul.
与SHE.Mul相同.
解密算法.FHE.Dec.
给定SK和密文c,计算输出消息比特m.
(1) 计算ui,j=[<(2σc×yi,j) mod x>/2σ]2,这里,ui,j保留σ= (q+1)
(q+1) 位比特小数,且ui,j最接近数(c×yi,j) mod x;
位比特小数,且ui,j最接近数(c×yi,j) mod x;
(2) 计算${{\bar{u}}_{i,j}}={{u}_{i,j}}\times {{\omega }_{i,j}};$
(3) 计算每个小块和${{\bar{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\bar{u}}}_{i,j}}};$
(4) 计算和$\bar{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\bar{u}}}_{i}}}]}_{2}};$
(5) 输出明文$m={{[c\bmod x]}_{2}}\oplus {{\bar{u}}_{0}}\oplus {{\bar{u}}_{-1}}$,这里,数$\bar{u}={{\bar{u}}_{0}}.{{\bar{u}}_{-1}}.....{{\bar{u}}_{-\sigma }}.$
密文刷新算法.FHE.Recrypt(PK,c).
(1) 计算ui,j=[<(2σc×yi,j) mod x>/2σ]2;
(2) 转换ui,j为密文形式的数${{\vec{u}}_{i,j}}={{u}_{i,j}}\times {{\vec{\omega }}_{i,j}};$
(3) 计算小块密文形式的和数${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\vec{u}}}_{i,j}}};$
(4) 使用对称多项式方法[2, 7]计算密文形式的和数$\vec{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\vec{u}}}_{i}}}]}_{2}};$
(5) 输出新密文${{c}_{new}}={{[c\bmod x]}_{2}}\oplus {{\vec{u}}_{0}}\oplus {{\vec{u}}_{-1}},$这里设密文形式的数$\vec{u}={{\vec{u}}_{0}}.{{\vec{u}}_{-1}}.....{{\vec{u}}_{-\sigma }}.$
评论5.1.在解密或密文刷新时,计算ui,j时保留到最接近σ位比特小数,因此,其每个误差至多为$\frac{1}{{{2}^{\sigma +1}}}.$而在这些ui,j中,仅有θ个ωi,j为1,故,舍入产生的误差至多为$\frac{\theta }{{{2}^{\sigma +1}}}.$
为了保证解密或密文刷新的正确,即${{[\langle \sum\nolimits_{i=1}^{\theta }{\sum\nolimits_{j=1}^{\Theta /\theta }{{{\omega }_{i,j}}{{u}_{i,j}}}}\rangle]}_{2}}={{[\langle c\times {{h}^{-1}}\rangle \bmod x]}_{2}},$故要求参数满足条件:
$$|\langle c\times {{h}^{-1}}\rangle \bmod x-(c\times {{h}^{-1}})\bmod x| <\frac{1}{2\theta }.$$
5.3 FHE正确性算法FHE.KeyGen,FHE.Enc,FHE.Add,FHE.Mul的正确性易于由SHE.KeyGen,SHE.Enc,SHE.Add,SHE.Mul的正确性得到.
解密算法FHE.Dec的正确性可由第5.1节的压扁解密电路得到,FHE.Recrypt的正确性由解密算法FHE.Dec得到.这两种算法之间的差异在于:FHE.Dec直接使用私钥SK,而FHE.Recrypt使用SK的比特密文形式.结果是,FHE.Dec得到密文中的明文比特,而FHE.Recrypt得到密文中明文比特的新密文.
定理5.1.设θ(ρ+logk+logθ+1)≤λ,则新密文bi=FHE.Recrypt(PK,ci),i=1,2与密文ci具有相同的明文比特,并且b1,b2能够进行一次同态密文乘法运算.
证明:比较两种算法FHE.Recrypt,FHE.Dec可以看出,FHE.Recrypt是FHE.Dec在密文形式下解密.故定理前半部分仅需证明FHE.Recrypt能够在密文形式下正确实现FHE.Dec.
步骤(1)
该步与FHE.Dec的步骤(1)相同.
步骤(2)
该步将ωi,j的密文${{\vec{\omega }}_{i,j}}$与ui,j中每个比特相乘,从而得到${{\vec{u}}_{i,j}}$.如果ωi,j为0,则${{\vec{u}}_{i,j}}$是数0的密文形式;如果ωi,j为1,则${{\vec{u}}_{i,j}}$就是ui,j的密文形式.因此,步骤(2)的结果就是FHE.Dec的步骤(2)中结果的密文形式.
步骤(3)
该步计算小块密文形式的和数,这里,每个小块中有且仅有一个ωi,j为1,故在密文形式的数${{\vec{u}}_{i,j}}$中有且仅有一个非零数,即,密文数${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\vec{u}}}_{i,j}}}$等于某个${{\vec{u}}_{i,j}}$所以,密文数可直接相加,无需考虑进位问题.而FHE.Dec(3)和${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\vec{u}}}_{i,j}}}$中有且仅有一个非零数,与${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\vec{u}}}_{i,j}}}$中非零密文数相对应.所以,步骤(3)的结果也是FHE.Dec (3)中结果的密文形式.
步骤(4)
计算密文形式的和数$\vec{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\vec{u}}}_{i}}}]}_{2}}$.我们采用文献[7]中的一般加法(grade-school addition,如图1所示)求θ个密文数和:首先,将θ个密文数安排成θ行、σ+1列,这些列从左到右依次对应于第0,-1,…,-σ位;然后,使用第2.3节中计算对称多项式的动态规划算法依次计算从右(第-σ位)到左(第0位)的比特和,第-j列进位到第-j+t列的比特值是第-j列比特值的2τ度的初等对称多项式.因为σ= log(θ+1)
log(θ+1) ,故在按列序(即-σ列、-σ+1列,直到-1列)求和时,需要计算该列向左最大进位数t分别为σ-1,σ-2,…,1.因此,在计算相应列时,这些列上的比特数分别为θ,θ+1,…,θ+σ-1.
,故在按列序(即-σ列、-σ+1列,直到-1列)求和时,需要计算该列向左最大进位数t分别为σ-1,σ-2,…,1.因此,在计算相应列时,这些列上的比特数分别为θ,θ+1,…,θ+σ-1.
因为如果第-j列有m个比特,则计算这些比特上所有直到2t度的初等对称多项式需要使用至多m2t次乘法,因此,这一步计算需要的乘法总数至多为$\theta {{2}^{\sigma -1}}+\sum\nolimits_{t=1}^{\sigma -1}{(\theta +t){{2}^{\sigma -t}}}=O({{\theta }^{2}}).$
为简单起见,我们取θ=15,σ= log(θ+1)
log(θ+1) =4,图1中,方块中数字为计算相应比特密文需要的多项式度数.
=4,图1中,方块中数字为计算相应比特密文需要的多项式度数.

|
图1 密文数一般加法示意图 Fig.1 Grade-School addition for encrypted data |
尽管存在需要更少乘法次数的其他加法,然而上述一般加法使用更小度数的多项式.因此,下面实现全同态方案时,我们仍然使用这种一般加法.
步骤(5)
计算最接近密文形式的数$\vec{u}={{\vec{u}}_{0}}.{{\vec{u}}_{-1}}.....{{\vec{u}}_{-\sigma }}$模2整数的密文${{\vec{u}}_{0}}\oplus {{\vec{u}}_{-1}}$,即:等价于密文形式计算<c×h-1> mod x,相当于FHE.Dec步骤(5)中的明文计算${{\bar{u}}_{0}}\oplus {{\bar{u}}_{-1}}.$最后,将比特[c mod x]2直接加到密文${{\vec{u}}_{0}}\oplus {{\vec{u}}_{-1}}$的常系数项上.
现在分析新密文中噪声多项式的大小,进而确定新密文能够再进行至少一次同态密文计算.
根据文献[7]中的对称多项式计算方法可知(如图1所示),计算θ个密文数和至多需要计算θ度对称多项式.易于验证:表示密文加法的度为q的单项式数目至多为$\left( \begin{matrix} \theta \\ \left\lceil \theta /2 \right\rceil \\ \end{matrix} \right)\times \left( \begin{matrix} \theta \\ \left\lceil \theta /4 \right\rceil \\ \end{matrix} \right)\times ...\times \left( \begin{matrix} \theta \\ 1 \\ \end{matrix} \right),$它小于2θlogθ.而在度为θ的单项式产生的密文中,噪声多项式的极大范数至多为kθ-12θr=2θr+(θ-1)logk.因此,在密文刷新算法输出密文的噪声多项式极大范数至多为2θρ+(θ-1)logk+θlogθ.为实现全同态加密,还需要密文刷新后新产生密文必须能够进行一次同态乘法运算,故,密文噪声极大范数至多为22θr+(2θ-1)logk+2θlogθ.
因此,为了正确解密,由引理3.2和条件$|\langle c\times {{h}^{-1}}\rangle \bmod x-(c\times {{h}^{-1}})\bmod x| <\frac{1}{2\theta }$,需要满足22θρ+(2θ-1)logk+2θlogθ≤2λ/(2kθ),即,2q(ρ+logk+logθ+1)≤λ.
5.4 FHE的安全性 5.4.1 稀疏子集和的格攻击在上述FHE方案中,除了KDM假设和因式分解难度假设,还引入了稀疏子集和问题SSSP假设.
在SSSP问题中,攻击者需求解方程$\sum\nolimits_{j=1}^{\Theta }{{{\omega }_{j}}{{y}_{j}}}={{h}^{-1}}\bmod \text{ }2.$这里假定攻击者知道h-1和集合${{y}_{j}}\in {{R}_{\mathbb{R},\delta }},$ $j\in [\Theta]$,并且私钥ω=(ω1,…,ωΘ)具有小Hamming权重θ.对于SSSP问题,易于构造行向量的格Li: $${{L}_{i}}=\left( \begin{matrix} {{2}^{\delta +1}} & 0 & 0 & \cdots & 0 \\ -{{({{2}^{\delta }}{{h}^{-1}})}_{i}} & 1 & 0 & \cdots & 0 \\ {{({{2}^{\delta }}{{y}_{1}})}_{i}} & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{({{2}^{\delta }}{{y}_{\Theta }})}_{i}} & 0 & 0 & \cdots & 1 \\ \end{matrix} \right),i\in [k].$$ 这里,(h-1)i,(yj)i,j∈[Θ]分别为h-1,yj的第i项.
在格Li中,v=(0,1,ω1,…,ωΘ)一般为最短长度向量,其范数为$\sqrt{\theta +1}.$因为格Li的行列式为2δ+1,则由
Minkowsky定理可知,格Li的第二短长度向量的范数大约为(2δ+1)1/Θ.因此,当Θ足够大时,目前格归约算法无法得到向量v=(0,1,ω1,…,ωΘ).
实际上,在文献[2, 7, 17]的FHE方案中,SSSP是隐藏的SSSP(HSSSP),即,敌手并不知道需要求解的子集和值.因此,即使存在有效求解SSSP算法,该算法也不一定能够求解HSSSP.本文考虑HSSSP的原因在于:一方面,在文献[2, 7, 17]的FHE方案中,SSSP问题易于受到格归约攻击,因为SSSP构造的格中最短长度向量通常为SSSP的解;另一方面,使用HSSSP假设能够减少公钥大小.
在文献[4, 7]中,当针对FHE方案安全进行分析时,作者们认为稀疏子集和问题存在生日攻击问题.生日攻击原指一群人中发生两人为同一天生日的概率,这里,同一天生日是指一年365天中任意一天发生两人生日相同均可[61].
给定$y=({{y}_{1}},...,{{y}_{\Theta }}),{{y}_{j}}\in {{R}_{\mathbb{R},\delta }},j\in [\Theta]$和h-1,我们可以定义Hash函数${{w}_{y}}(x)=\sum\nolimits_{j=1}^{\Theta }{{{x}_{j}}{{y}_{j}}}\bmod 2,x\in {{\{0,1\}}^{\Theta }}$.针对 wy(x)的生日攻击,是指随机产生多少个Hash值会以高概率发生一次碰撞.易于计算,需要随机产生(2δ+1)k/2个Hash值发生一次碰撞的概率大约为0.328(等价于生日攻击中的$\sqrt{365}$).
在稀疏子集和问题中并不存在生日攻击问题,因为方程$\sum\nolimits_{j=1}^{\Theta }{{{x}_{j}}{{y}_{j}}}={{h}^{-1}}\bmod 2$的解为x∈{0,1}Θ,所以稀疏子集和问题是该方程有多少解.根据剩余Hash引理2.1,如果y=(y1,…,yΘ)和x都是随机的,则$\sum\nolimits_{j=1}^{\Theta }{{{x}_{j}}{{y}_{j}}}\bmod 2$在${{R}_{\mathbb{R},\delta }}$几乎也是均匀的.尽管稀疏子集和问题中存在一个Hamming权重θ的解ω=(ω1,…,ωΘ)满足${{R}_{\mathbb{R},\delta }}$但对于不等于ω的任意x,$\sum\nolimits_{j=1}^{\Theta }{{{x}_{j}}{{y}_{j}}}\bmod 2$在${{R}_{\mathbb{R},\delta }}$上是几乎均匀的.因此,集合{0,1}Q中不等于w的任意x满足方程$\sum\nolimits_{j=1}^{\Theta }{{{x}_{j}}{{y}_{j}}}={{h}^{-1}}\bmod 2$的概率几乎为0,即,以概率为1仅有ω一个解.所以,通过蛮力攻击必须猜测到解w才可行,即:在FHE中,猜测隐藏SSSP问题的复杂性为O((Θ/q)q),而不是文献[4, 7]中给出的O((Θ/θ)θ/2).
6 批全同态加密方案在FHE方案中,我们能够扩展明文消息空间从{0,1}到{0,1}k,以减少密文膨胀率从O(kρ2)到O(ρ2).给定消息m∈{0,1}k,我们映射它到多项式$m(x)=\sum\nolimits_{i=0}^{k-1}{{{m}_{i}}{{x}^{i}}}.$加密算法FHE.Enc变为$c=(m(x)+2r+2\sum{{{r}_{i,j}}{{f}_{1,i}}}{{f}_{2,j}})\bmod {{f}_{0}}$.解密算法(FHE.Dec(SK,c))变为:
(1) 计算ui,j=[<2scxyi,j>/2σ]2,即ui,j最接近多项式c×yi,j;
(2) 计算${{\bar{u}}_{i,j}}={{u}_{i,j}}\times {{\omega }_{i,j}};$
(3) 计算每个小块和${{\bar{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\bar{u}}}_{i,j}}};$
(4) 计算多项式和$\bar{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\bar{u}}}_{i}}}]}_{2}};$
(5) 输出明文$m(x)={{[c]}_{2}}\oplus {{\bar{u}}_{0}}\oplus {{\bar{u}}_{-1}},$这里,记$\bar{u}={{\bar{u}}_{0}}.{{\bar{u}}_{-1}}.....{{\bar{u}}_{-\sigma }},{{\bar{u}}_{j}}$为多项式$\bar{u}$中每个系数按比特展开时,第j比特位组成的多项式.
如果需要进行比特密文计算,则在同态密文计算之前,首先将多比特密文解包成单个比特密文,然后再按照FHE算法进行正常密文同态计算.
密文解包算法.FHE.Unpack(PK,c).
(1) 计算ui,j=[<2sc×yi,j>/2σ]2;
(2) 转换ui,j为密文形式多项式${{\vec{u}}_{i,j}}={{u}_{i,j}}\times {{\vec{\omega }}_{i,j}};$
(3) 计算小块密文形式多项式和${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{\Theta /\theta }{{{{\vec{u}}}_{i,j}}};$
(4) 使用对称多项式方法[2, 7]计算密文形式多项式和$\vec{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\vec{u}}}_{i}}}]}_{2}};$
(5) 输出新密文多项式${{c}_{new}}(x)={{[c]}_{2}}\oplus {{\vec{u}}_{0}}\oplus {{\vec{u}}_{-1}}$,cnew(x)中的k个比特密文系数可以单独参加后续比特密文计算.这里,记密文形式多项式$\vec{u}={{\vec{u}}_{0}}.{{\vec{u}}_{-1}}.....{{\vec{u}}_{-\sigma }},{{\vec{u}}_{j}}$为多项式$\vec{u}$中每个系数按比特展开时,第j比特位组成的密文多项式.
在密文同态计算结束后,需要将k个比特密文打包成一个新密文.假定ci,i∈[k]为比特密文,则打包密文为
$$c(x)=(\sum\nolimits_{i=1}^{k}{{{c}_{i}}\times {{x}^{i-1}}})\bmod ({{x}^{k}}+1)\bmod {{f}_{0}}.$$
7 基于AILP的FHE在基于PAILP的FHE中,公钥中包括无噪声的h倍数多项式f0=g0h,使得方案安全性依赖于大整数分解难度假设.然而,目前存在量子多项式时间算法分解大整数[62].实际上,我们可以构造基于近似理想格的全同态加密方案.然而,目前我们并不能归约基于AILP的SHE1安全性到近似理想格问题.但SHE1安全性能够归约到部分近似理想格问题,即,基于AILP的SHE1安全性不比SHE的安全性低.因为从SHE1构造全同态加密方案FHE1的方法与构造FHE的方法相同,所以下面仅给出基于AILP的SHE1方案.
密钥生成算法.SHE1.KeyGen.
(1) 随机选择多项式h∈R满足h mod 2=1和||h||∞=2λ;
(2) 随机选择gj,ej∈R,j∈[τ2]满足||gj||∞∈[2η],||ej||∞∈[2ρ],计算输出fj=hgj+ej.设f0=hg0+2e0满足||g0||∞∈[2η],||e0||∞∈[2ρ],||f0||∞≥||fj||∞和f0 mod 2≠0;
(3) 随机选择β=O((λ+η)/ρ)对ai,ei∈R,i∈[β]满足||ai||∞≈2η+ρi和||ei||∞∈[2ρ],计算$\{{{d}_{i}}={{a}_{i}}h+2{{e}_{i}}\}_{i=1}^{\beta }.$计算验证$||d_{i}^{-1}|{{|}_{\infty }}\approx {{2}^{-(\lambda +\eta +\rho i)}},$如果不满足,则重新选择ai,ei∈R;
(4) 输出公钥$pk=(k,{{f}_{0}},{{\{{{f}_{j}}\}}_{j\in [{{\tau }^{2}}]}},{{\{{{d}_{i}}\}}_{i\in [\beta]}})$和私钥sk=(h).
加密算法.SHE1.Enc.
给定公钥pk和比特m∈{0,1},随机选择rj∈R,j∈[τ2]和r∈R满足||rj||∞∈[2ρ]和||r||∞∈[2ρ].计算输出密文:
$$c=(m+2r+\sum{2{{r}_{j}}{{f}_{j}}})\bmod {{f}_{0}}.$$
密文加算法.SHE1.Add.
给定公钥pk和密文c1,c2,计算输出密文c=(c1+c2) mod f0.
密文乘算法.SHE1.Mul.
给定公钥pk和密文c1,c2,计算输出密文c=Opt(c1×c2),这里,Opt是类似于文献[2]中的优化方法,即:
c=(c1×c2) mod dt mod dt-1 … mod d1 mod f0.
解密算法.SHE1.Dec.
给定sk和密文c,计算输出m=[<c×h-1> mod x]2⊕[c mod x]2.
评论7.1.
(1) SHE1计算c mod di实际上是计算c mod Rot(di),即,将$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}$映射到格基Rot(di)的平行四边形内部;
(2) 因为SHE1.Enc中的$||m+2r+\sum{2{{r}_{j}}{{f}_{j}}}|{{|}_{\infty }}/||{{f}_{0}}|{{|}_{\infty }}$较小,即,mod f0时引入噪声范数较小,所以能够直接计算$c=(m+2r+\sum{2{{r}_{j}}{{f}_{j}}})\bmod {{f}_{0}}.$但在密文乘法时,||c1×c2||∞=O(22(λ+η))远大于||f0||∞,如果在这种情况下直接计算(c1×c2) mod f0,则引入的噪声太大,使得明文不能正确恢复.因此,我们使用Opt优化算法将c1×c2按阶梯分步映射,并最终映射到格基Rot(f0)的平行四边形内部.注意:这也是SHE1.Enc使用公钥元素线性函数的原因;而且为了避免格攻击,公钥元素fj的数目需要τ2=O(ρ4);
(3) h∈R仅需满足h mod 2=1,不要求det(Rot(h))为大素数或难分解合数,因为对手不知道det(Rot(h));另一方面,为了避免中国剩余定理的攻击,需要det(Rot(h))没有小因子(如最小因子大于2ρ).因为若det(Rot(h))中存在小因子积大于噪声多项式的极大范数,则敌手可针对每个因子猜测其噪声多项式,然后利用中国剩余定理求解出真正噪声多项式,并进而去除它.
引理7.1.SHE1.KeyGen算法运行在概率多项式时间.
证明:易于看出,SHE1.KeyGen的步骤(1)、步骤(2)运行在多项式时间,SHE1.KeyGen的步骤(3)实际上是要求di的逆$d_{i}^{-1}$的长度满足条件$||d_{i}^{-1}|{{|}_{\infty }}\approx {{(||{{d}_{i}}|{{|}_{\infty }})}^{-1}}.$因为||di||∞≈2λ+η+ρi,即,要求$||d_{i}^{-1}|{{|}_{\infty }}\approx {{2}^{-(\lambda +\eta +\rho i)}}.$设p=res(di,xk+1)为多项式di,xk+1的结式(resu ltant),易于验证p=det(Rot(di)).由文献[3]中的引理1可知:$||pd_{i}^{-1}|{{|}_{\infty }}\le ||{{d}_{i}}||_{2}^{k-1}||{{x}^{k}}+1||_{2}^{k-1},$并且以高概率$p\approx ||{{d}_{i}}||_{2}^{k}||{{x}^{k}}+1||_{2}^{k-1},$所以$||d_{i}^{-1}|{{|}_{\infty }}\le ||{{d}_{i}}||_{2}^{-1}\approx 1/(\sqrt{k}{{2}^{(\lambda +\eta +\rho i)}})\approx {{2}^{-(\lambda +\eta +\rho i)}}.$因此,SHE1.KeyGen能够在概率多项式时间内产生公钥和私钥.
引理7.2.如果||d-1||∞≈(||d||∞)-1和||c||∞/||d||∞≤2ρ,则c mod d=c-qd中的q满足||q||∞≈k2ρ.
证明:因为c mod d=c-qd,则q=d-1(c-c mod d).所以:
$$\begin{align} & ||q|{{|}_{\infty }}=||{{d}^{-1}}(c-c\bmod d)|{{|}_{\infty }} \\ & \quad \ \ \text{ }\,\le k||{{d}^{-1}}|{{|}_{\infty }}||(c-c\bmod d)|{{|}_{\infty }} \\ & \quad \ \ \,\text{ }\le k||{{d}^{-1}}|{{|}_{\infty }}(||c|{{|}_{\infty }}+||c\bmod d|{{|}_{\infty }}) \\ & \quad \ \ \,\text{ }\le k||{{d}^{-1}}|{{|}_{\infty }}(||c|{{|}_{\infty }}+||d|{{|}_{\infty }}) \\ & \quad \ \ \text{ }\,\approx k{{2}^{\rho }}.\\ \end{align}$$
证毕.
从引理7.2可以看出,Opt算法每次模di在密文中增加的噪声多项式的范数较小.因此易于验证,密文c=Opt(c1×c2)中的噪声多项式大小由密文c1,c2中噪声多项式积的大小控制.
所以,只要选定适当参数,方案SHE1支持有点同态密文计算.然后,使用Gentry引导技术,易于将SHE1转换为全同态加密方案FHE1.
8 实现FHE 8.1 实现FHE我们使用NTL库[26]实现基于AILP/PAILP的FHE.在实现FHE时,主要考虑因素是在一定安全级别上(如攻击难度为272),尽可能地提高方案实用性,包括密文膨胀率、同态计算复杂性、公钥大小等.
由第5节的FHE可知,方案的安全性依赖于如下3个方面:
(1) 大整数分解难度.目前,在经典计算机上分解方案中使用的大整数仍然不够现实;
(2) 隐藏稀疏子集和攻击难度.使用文献[7]中的优化技术,将稀疏子集分成小块,每个小块中仅一个元素属于私钥的稀疏子集和,本文所有实验都取Θ=960,q=15,B=Θ/q=64,s= log(θ+1)
log(θ+1) =4.根据本文稀疏子集和的生日攻击分析,蛮力猜测攻击复杂性估计为6415=290;
=4.根据本文稀疏子集和的生日攻击分析,蛮力猜测攻击复杂性估计为6415=290;
(3) 蛮力攻击PAILP的噪声多项式,该攻击复杂性约为2kρ,r=log||e||∞或为时间和空间复杂性都为2(k-1)r (根据第4.2.4节分析).蛮力攻击AILP的复杂性至少为2kρ.
下面描述当k=4时,实现FHE方案中各个参数值大小.
首先估计log||h||∞的大小.当加密私钥比特的密文中噪声多项式满足ρ=log||2e||∞时,则FHE.Recrypt算法计算小块B个密文和数${{\vec{u}}_{i}}=\sum\nolimits_{j=1}^{B}{{{{\vec{u}}}_{i,j}}}$中的噪声大小变为ρ'=ρ+6.计算θ=15个密文数和$\vec{u}={{[\sum\nolimits_{i=1}^{\theta }{{{{\vec{u}}}_{i}}}]}_{2}}$需要使用度为15的对称多项式.易于计算,一个度为15的多项式密文的噪声大小为15ρ'+28.根据文献[7]的分析,度为15的多项式的密文数目至多为234.故密文数和$\vec{u}$中的噪声大小至多为15ρ'+28+34=15ρ'+62.因为密文刷新后需要能支持至少一次密文乘法运算,故ρ²=2(15ρ'+62)+2=30ρ'+126.又因为要求多项式(c×h-1) mod x的每个系数与整数的最小距离在1/(2θ)内,故log||h-1||∞≤-(30ρ'+131).
所以,log||h||∞应略大于30ρ'+131,以满足条件log||h-1||∞≤-(30ρ'+131).
如果设ρ=24,则λ=log||h||∞=30ρ'+126≈1036,η≈51800>λ,τ=512.
为了提高效率,每次加密$c=(m+2r+2\sum{{{r}_{i,j}}{{f}_{1,i}}}{{f}_{2,j}})\bmod {{f}_{0}}$时,从τ2对中随机选择20个ri,j∈{-1,1},其余都为
0,并且||2r||∞∈[2ρ].
类似地,对于其他k,ρ不同取值的组合,不难计算其他相应参数值的大小.
8.2 FHE性能比较我们通过表1和表2给出本文与以前FHE的性能比较.表1给出实现FHE方案的具体运行环境,表2中给出实现的FHE方案性能情况.从表2可以看出,基于近似理想格的FHE方案比已有方案性能更好.
| 表1 实现FHE方案的具体运行环境 Table 1 Concrete running setting of implementing FHE schemes |
| 表2 FHE方案性能比较 Table 2 Performance comparison of implementing FHE schemes |
本文首先构造了基于PAILP的SHE,并归约证明SHE安全性到求解PAILP;其次,使用Gentry引导技术转换SHE到FHE;然后,分别构造了基于PAILP的批同态加密方案和基于AILP的全同态加密方案;最后,实现了基于近似理想格的全同态加密方案,并与现有全同态加密方案的性能进行了比较.
我们注意到,Coron,Naccache和Tibouchi[5]使用模切换技术[11]构造了DGHV型的无引导层次全同态加密方案.方案构造的关键是文献[5]中的引理4和引理5,这两个引理给出了在密文状态下如何实现近似GCD问题从私钥p到私钥p'的正确切换,并且保证切换后近似GCD问题的噪声从r减少到约为r×(p'/p)≈r×2-ρ.因为本文的近似理想格问题是近似GCD问题的扩展,易于验证文献[5]中的引理4和引理5在近似理想格上同样成立.在自适应文献[5]中整数近似GCD上的引理证明到近似理想格上时,需将整数近似GCD替换成近似理想格,参数大小分析时使用的绝对值替换成近似理想格上的极大范数,而且与整数上条件p'/p≈2-ρ类似,需要保证进行切换的近似理想格h',h满足条件||h'/h||∞≈2-ρ,证明过程完全相同.因此,使用文献[5]中同样的方法,我们能够自适应地构造出基于近似理想格的无引导的层次全同态加密方案.当然,基于近似理想格的无引导的层次全同态加密方案效率会更高,因为可以使用||h||∞更小的私钥h.
本文需进一步研究的问题:证明基于AILP的SHE安全性;研究分析问题AILP/PAILP的求解难度,并建立AILP与理想格问题之间的关系;研究分析基于AILP/PAILP的FHE方案的实际安全性.
致谢 在此,我们感谢本文的匿名审稿专家所提供的宝贵修改意见.本文的数值计算得到了中国科学技术大学超级计算中心的计算支持和帮助,作者在此一并表示感谢.
| [1] | Gentry C.Fully homomorphic encryption using ideal lattices.In: Mitzenmacher M, ed.Proc.of the 41st Annual ACM Symp.on Theory of Computing (STOC 2009).New York: Association for Computing Machinery, 2009.169-178.doi: 10.1145/1536414.1536440 |
| [2] | van Dijk M, Gentry C, Halevi S, Vaikuntanathan V.Fully homomorphic encryption over the integers.In: Gilbert H, ed.Proc.of the EUROCRYPT 2010.LNCS 6110, Heidelberg: Springer-Verlag, 2010.24-43.doi: 10.1007/978-3-642-13190-5_2 |
| [3] | Smart NP, Vercauteren F.Fully homomorphic encryption with relatively small key and ciphertext sizes.In: Nguyen PQ, Pointcheval D, eds.Proc.of the Public Key Cryptography (PKC 2010).LNCS 6056, Heidelberg: Springer-Verlag, 2010.420-443.doi: 10.1007/978-3-642-13013-7_25 |
| [4] | Coron JS, Mandal A, Naccache D, Tibouchi M.Fully homomorphic encryption over the integers with shorter public keys.In: Rogaway P, ed.Proc.of the CRYPTO 2011.LNCS 6841, Heidelberg: Springer-Verlag, 2011.487-504.doi: 10.1007/978-3-642- 22792-9_28 |
| [5] | Coron JS, Naccache D, Tibouchi M.Public key compression and modulus switching for fully homomorphic encryption over the integers.In: Pointcheval D, Johansson T, eds.Proc.of the EUROCRYPT 2012.LNCS 7237, Heidelberg: Springer-Verlag, 2012.446-464.doi: 10.1007/978-3-642-29011-4_27 |
| [6] | Cheon JH, Coron JS, Kim J, Lee MS, Lepoint T, Tibouchi M, Yun A.Batch fully homomorphic encryption over the integers.In: Johansson T, Nguyen P, eds.Proc.of the EUROCRYPT 2013.LNCS 7881, Heidelberg: Springer-Verlag, 2013.315-335.doi: 10.1007/978-3-642-38348-9_20 |
| [7] | Gentry C, Halevi S.Implementing Gentry's fully-homomorphic encryption scheme.In: Paterson KG, ed.Proc.of the EUROCRYPT 2011.LNCS 6632, Heidelberg: Springer-Verlag, 2011.129-148.doi: 10.1007/978-3-642-20465-4_9 |
| [8] | Gentry C, Halevi S.Fully homomorphic encryption without squashing using depth-3 arithmetic circuits.In: Proc.of the 2011 IEEE 52nd Annual Symp.on Foundations of Computer Science (FOCS 2011).Washington: IEEE Computer Society, 2011.107-116.doi: 10.1109/FOCS.2011.94 |
| [9] | Brakerski Z, Vaikuntanathan V.Fully homomorphic encryption from ring-LWE and security for key dependent messages.In: Rogaway P, ed.Proc.of the CRYPTO 2011.LNCS 6841, Heidelberg: Springer-Verlag, 2011.505-524.doi: 10.1007/978-3-642- 22792-9_29 |
| [10] | Brakerski Z, Vaikuntanathan V.Efficient fully homomorphic encryption from (Standard) LWE.In: Proc.of the 2011 IEEE 52nd Annual Symp.on Foundations of Computer Science (FOCS 2011).Washington: IEEE Computer Society, 2011.97-106.doi: 10.1109/FOCS.2011.12 |
| [11] | Brakerski Z, Gentry C, Vaikuntanathan V.(Leveled) Fully homomorphic encryption without bootstrapping.In: Proc.of the 3rd Innovations in Theoretical Computer Science Conf.(ITCS 2012).New York: Association for Computing Machinery, 2012.309-325.doi: 10.1145/2090236.2090262 |
| [12] | Gentry C, Halevi S, Smart NP.Better bootstrapping in fully homomorphic encryption.In: Fischlin M, Buchmann J, Manulis M, eds.Proc.of the Public Key Cryptography (PKC 2012).LNCS 7293, Heidelberg: Springer-Verlag, 2012.1-16.doi: 10.1007/978-3- 642-30057-8_1 |
| [13] | Gentry C, Halevi S, Smart NP.Fully homomorphic encryption with polylog overhead.In: Pointcheval D, Johansson T, eds.Proc.of the EUROCRYPT 2012.LNCS 7237, Heidelberg: Springer-Verlag, 2012.465-482.doi: 10.1007/978-3-642-29011-4_28 |
| [14] | Gentry C, Halevi S, Smart NP.Homomorphic evaluation of the AES circuit.In: Safavi-Naini R, Canetti R, eds.Proc.of the CRYPTO 2012.LNCS 7417, Heidelberg: Springer-Verlag, 2012.850-867.doi: 10.1007/978-3-642-32009-5_49 |
| [15] | Brakerski Z.Fully homomorphic encryption without modulus switching from classical GapSVP.In: Safavi-Naini R, Canetti R, eds.Proc.of the CRYPTO 2012.LNCS 7417, Heidelberg: Springer-Verlag, 2012.868-886.doi: 10.1007/978-3-642-32009-5_50 |
| [16] | Lopez-Alt A, Tromer E, Vaikuntanathan V.On-the-Fly multiparty computation on the cloud via multikey fully homomorphic encryption.In: Proc.of the 44th Annual ACM Symp.on Theory of Computing (STOC 2012).New York: Association for Computing Machinery, 2012.1219-1234.doi: 10.1145/2213977.2214086 |
| [17] | Stehle D, Steinfeld R.Faster fully homomorphic encryption.In: Abe M, ed.Proc.of the ASIACRYPT 2010.LNCS 6477, Heidelberg: Springer-Verlag, 2010.377-394.doi: 10.1007/978-3-642-17373-8_22 |
| [18] | Gentry C, Sahai A, Waters B.Homomorphic encryption from learning with errors: Conceptually-Simpler, asymptotically-faster, attribute-based.In: Canetti R, Garay JA, eds.Proc.of the CRYPTO 2013.LNCS 8042, Heidelberg: Springer-Verlag, 2013.75-92.doi: 10.1007/978-3-642-40041-4_5 |
| [19] | Brakerski Z, Vaikuntanathan V.Lattice-Based FHE as secure as PKE.In: Proc.of the 5th Conf.on Innovations in Theoretical Computer Science (ITCS 2014).New York: Association for Computing Machinery, 2014.1-12.doi: 10.1145/2554797.2554799 |
| [20] | Gu CS, Gu JX.Cryptanalysis of the smart-vercauteren and Gentry-Halevi's fully homomorphic encryption.Int'l Journal of Security and Its Applications, 2012,6(2):103-108. |
| [21] | Nguyen P, Stehle D.LLL on the average.In: Hess F, Pauli S, Pohst M, eds.Proc.of the ANTS 2006.LNCS 4076, Heidelberg: Springer-Verlag, 2006.238-256.doi: 10.1007/11792086_18 |
| [22] | Lenstra HW, Lenstra AK, Lovasz L.Factoring polynomials with rational coefficients.Mathematische Annalen, 1982,261(4): 515-534.doi: 10.1007/BF01457454 |
| [23] | Hu YP, Wang FH.An attack on a fully homomorphic encryption scheme, ePrint archive.Technical Report, 2012/561, 2012.http://eprint.iacr.org/2012/561 |
| [24] | Chen Y, Nguyen PQ.Faster algorithms for approximate common divisors: Breaking fully homomorphic encryption challenges over the integers.In: Pointcheval D, Johansson T, eds.Proc.of the EUROCRYPT 2012.LNCS 7237, Heidelberg: Springer-Verlag, 2012.502-519.doi: 10.1007/978-3-642-29011-4_30 |
| [25] | Lauter K, Naehrig M, Vaikuntanathan V.Can homomorphic encryption be practical.In: Proc.of the 3rd ACM Workshop on Cloud Computing Security Workshop (CCSW 2011).New York: Association for Computing Machinery, 2011.113-124.doi: 10.1145/ 2046660.2046682 |
| [26] | Shoup V.NTL: A library for doing number theory.Version 7.0.2, 2009.http://shoup.net/ntl/ |
| [27] | Gu CS, Wu FS.On fully homomorphic encryption, approximate lattice problem and LWE.Int'l Journal of Cloud Computing and Services Science, 2013,2(1):1-15.doi: 10.11591/closer.v2i1.1339 |
| [28] | Zhang Y, Wen T, Guo Q, LI FK.Pair-Wise key establishment for wireless sensor networks based on fully homomorphic encryption.Journal on Communications, 2012,33(10):101-109 (in Chinese with English abstract). |
| [29] | Chen JY, Wang C, Zhang WM, Zhu YF.A secure image steganographic method in encrypted domain.Journal of Electronics & Information Technology, 2012,34(7):1721-1726 (in Chinese with English abstract).doi: 10.3724/SP.J.1146.2011.01240 |
| [30] | Sun ZW, Feng DG, Wu CK.An anonymous fingerprinting scheme based on additively homomorphic public key cryptosystem.Ruan Jian Xue Bao/Journal of Software, 2005,16(10):1816-1821 (in Chinese with English abstract).http://www.jos.org.cn/1000- 9825/16/1816.htm |
| [31] | Guang Y, Gu CX, Zhu YF, Zheng YH, Fei JL.Certificateless fully homomorphic encryption based on LWE problem.Journal of Electronics & Information Technology, 2013,35(4):988-993 (in Chinese with English abstract).doi: 10.3724/SP.J.1146.2012.01102 |
| [32] | Feng DG, Zhang M, Zhang Y, Xu Z.Study on cloud computing security.Ruan Jian Xue Bao/Journal of Software, 2011,22(1): 71-83 (in Chinese with English abstract).http://www.jos.org.cn/1000-9825/3958.htm doi: 10.3724/SP.J.1001.2011.03958 |
| [33] | Yu NH, Hao Z, Xu JJ, Zhang WM, Zhang C.Review of cloud computing security.Acta Electronica Sinica, 2013,41(2):371-381 (in Chinese with English abstract).doi: 10.3969/j.issn.0372-2112.2013.02.026 |
| [34] | Cheng FQ, Peng ZY, Song W, Wang SL, Cui YH.An efficient privacy-preserving rank query over encrypted data in cloud computing.Chinese Journal of Computers, 2012,35(11):2215-2227 (in Chinese with English abstract).doi: 10.3724/SP.J.1016.2012.02215 |
| [35] | Cai K, Zhang M, Feng DG.Secure range query with single assertion on encrypted data.Chinese Journal of Computers, 2011,34(11): 2093-2103 (in Chinese with English abstract).doi: 10.3724/SP.J.1016.2011.02093 |
| [36] | Zhu Q, Zhao T, Wang S.Privacy preservation algorithm for service-oriented information search.Chinese Journal of Computers, 2010,33(8):1315-1323 (in Chinese with English abstract).doi: 10.3724/SP.J.1016.2010.01315 |
| [37] | Regev O.On lattices, learning with errors, random linear codes, and cryptography.Journal of the ACM (JACM), 2009,56(6):1-40.doi: 10.1145/1060590.1060603 |
| [38] | Lyubashevsky V, Peikert C, Regev O.On ideal lattices and learning with errors over rings.In: Gilbert H, ed.Proc.of the EUROCRYPT 2010.LNCS 6110, Heidelberg: Springer-Verlag, 2010.1-23.doi: 10.1007/978-3-642-13190-5_1 |
| [39] | Alperin-Sheriff J, Peikert C.Practical bootstrapping in quasilinear time.In: Canetti R, Garay JA, eds.Proc.of the CRYPTO 2013.LNCS 8042, Heidelberg: Springer-Verlag, 2013.1-20.doi: 10.1007/978-3-642-40041-4_1 |
| [40] | Alperin-Sheriff J, Peikert C.Faster bootstrapping with polynomial error.In: Garay JA, Gennaro R, eds.Proc.of the CRYPTO 2014.LNCS 8616, Heidelberg: Springer-Verlag, 2014.297-314.doi: 10.1007/978-3-662-44371-2_17 |
| [41] | Halevi S, Shoup V.Algorithms in HElib.In: Garay JA, Gennaro R, eds.Proc.of the CRYPTO 2014.LNCS 8616, Heidelberg: Springer-Verlag, 2014.554-571.doi: 10.1007/978-3-662-44371-2_31 |
| [42] | Kannan R.Improved algorithms for integer programming and related lattice problems.In: Proc.of the 15th Annual ACM Symp.on Theory of Computing (STOC'83).New York: Association for Computing Machinery, 1983.193-206.doi: 10.1145/800061.808749 |
| [43] | Schnorr CP.A hierarchy of polynomial time lattice basis reduction algorithms.Theoretical Computer Science, 1987,53(2-3): 201-224.doi: 10.1016/0304-3975(87)90064-8 |
| [44] | Ajtai M, Kumar R, Sivakumar D.A sieve algorithm for the shortest lattice vector problem.In: Proc.of the 33rd Annual ACM Symp.on Theory of Computing (STOC 2001).New York: Association for Computing Machinery, 2001.601-610.doi: 10.1145/ 380752.380857 |
| [45] | Gama N, Howgrave-Graham N, Koy H, Nguyen PQ.Rankin's constant and blockwise lattice reduction.In: Dwork C, ed.Proc.of the CRYPTO 2006.LNCS 4117, Heidelberg: Springer-Verlag, 2006.112-130.doi: 10.1007/11818175_7 |
| [46] | Gama N, Nguyen P.Finding short lattice vectors within Mordell's inequality.In: Proc.of the 40th Annual ACM Symp.on Theory of Computing (STOC 2008).New York: Association for Computing Machinery, 2008.208-216.doi: 10.1145/1374376.1374408 |
| [47] | Gama N, Nguyen P.Predicting lattice reduction.In: Smart N, ed.Proc.of the EUROCRYPT 2008.LNCS 4965, Heidelberg: Springer-Verlag, 2008.31-51.doi: 10.1007/978-3-540-78967-3_3 |
| [48] | Nguyen P, Vidick T.Sieve algorithms for the shortest vector problem are practical.Journal of Mathematical Cryptology, 2008,2(2): 181-207. |
| [49] | Becker A, Gama N, Joux A.A sieve algorithm based on overlattices.LMS Journal of Computation and Mathematics, 2014, 17(Special Issue A):49-70.doi: 10.1112/S1461157014000229 |
| [50] | Micciancio D, Voulgaris P.Faster exponential time algorithms for the shortest vector problem.In: Proc.of the 21st Annual ACM- SIAM Symp.on Discrete Algorithms (SODA 2010).Society for Industrial and Applied Mathematics, 2010.1468-1480.http://dl.acm.org/citation.cfm?id=1873601.1873720&coll=DL&dl=ACM&CFID=715343813&CFTOKEN=29694473 |
| [51] | Wang XY, Liu MJ, Tian CL, Bi JG.Improved Nguyen-Vidick heuristic sieve algorithm for shortest vector problem.In: Proc.of the 6th ACM Symp.on Information, Computer and Communications Security (ASIACCS 2011).New York: Association for Computing Machinery, 2011.1-9.doi: 10.1145/1966913.1966915 |
| [52] | Ajtai M, Dwork C.A public-key cryptosystem with worst-case/average-case equivalence.In: Proc.of the 29th Annual ACM Symp.on Theory of Computing (STOC'97).New York: Association for Computing Machinery, 1997.284-293.doi: 10.1145/258533.258604 |
| [53] | Regev O.New lattice-based cryptographic constructions.Journal of the ACM, 2004,51(6):899-942.doi: 10.1145/1039488.1039490 |
| [54] | von zur Gathen J, Gerhard J.Modern Computer Algebra.3rd ed., Cambridge: Cambridge University Press, 2013. |
| [55] | Boyar J, Peralta R, Pochuev D.On the multiplicative complexity of Boolean functions over the basis (∧,⊕,1).Theoretical Computer Science, 2000,235(1):43-57.doi: 10.1016/S0304-3975(99)00182-6 |
| [56] | Hastad J, Impagliazzo R, Levin LA, Luby M.A pseudorandom generator from any one-way function.SIAM Journal on Computing, 1999,28(4):1364-1396.doi: 10.1137/S0097539793244708 |
| [57] | Vaikuntanathan V.Computing blindfolded: New developments in fully homomorphic encryption.In: Proc.of the 2011 IEEE 52nd Annual Symp.on Foundations of Computer Science (FOCS 2011).Washington: IEEE Computer Society, 2011.5-16.doi: 10.1109/FOCS.2011.98 |
| [58] | Howgrave-Graham N.Approximate integer common divisors.In: Silverman JH, ed.Proc.of the CaLC 2001.LNCS 2146, Heidelberg: Springer-Verlag, 2001.51-66.doi: 10.1007/3-540-44670-2_6 |
| [59] | Nguyen PQ, Vallée B.The LLL Algorithm: Survey and Applications.Heidelberg: Springer-Verlag, 2009.33-35.doi: 10.1007/ 978-3-642-02295-1 |
| [60] | Barak B, Haitner I, Hofheinz D, Ishai Y.Bounded key-dependent message security.In: Gilbert H, ed.Proc.of the EUROCRYPT 2010.LNCS 6110, Heidelberg: Springer-Verlag, 2010.423-444.doi: 10.1007/978-3-642-13190-5_22 |
| [61] | Goldwasser S, Bellare M.Lecture notes on cryptography.2008.249-250.http://cseweb.ucsd.edu/-mihir/papers/gb.html |
| [62] | Shor PW.Polynomial-Time algorithms for prime factorization and discrete logarithms on a quantum computer.SIAM Journal Computing, 1997,26(5):1484-1509.doi: 10.1137/S0097539795293172 |
| [63] | 张永,温涛,郭权,李凤坤.WSN中基于全同态加密的对偶密钥建立方案.通信学报,2012,33(10):100-109. |
| [64] | 陈嘉勇,王超,张卫明,祝跃飞.安全的密文域图像隐写术.电子与信息学报,2012,34(7):1721-1726.doi: 10.3724/SP.J.1146.2011.01240 |
| [65] | 孙中伟,冯登国,武传坤.基于加同态公钥密码体制的匿名数字指纹方案.软件学报,2005,16(10):1816-1821.http://www.jos.org.cn/1000-9825/16/1816.htm |
| [66] | 光炎,顾纯祥,祝跃飞,郑永辉,费金龙.一种基于LWE问题的无证书全同态加密体制.电子与信息学报,2013,35(4):988-993.doi: 10.3724/SP.J.1146.2012.01102 |
| [67] | 冯登国,张敏,张妍,徐震.云计算安全研究.软件学报,2011,22(1):71-83.http://www.jos.org.cn/1000-9825/3958.htm doi: 10.3724/ SP.J.1001.2011.03958 |
| [68] | 俞能海,郝卓,徐甲甲,张卫明,张驰.云安全研究进展综述.电子学报,2013,41(2):371-381.doi: 10.3969/j.issn.0372-2112.2013.02.026 |
| [69] | 程芳权,彭智勇,宋伟,王书林,崔一辉.云环境下一种隐私保护的高效密文排序查询方法.计算机学报,2012,35(11):2215-2227.doi: 10.3724/SP.J.1016.2012.02215 |
 2015, Vol.26
2015, Vol.26


