时序数据是数据挖掘中最常见的数据类型之一,在许多领域都有应用,如某河流的逐月径流量、当地月平均气温和降水量、我国的居民消费价格指数(CPI)和国内生产总值(GDP)、地震发生时多个观测点得到的波形序列等.对这些时序数据进行分析,可以得到一些有益的结论,如:通过研究河流历史流量、气温和降水量等特征,可以有效提高洪灾预测水平;利用CPI和GDP,可以分析国家或地区的通胀程度和经济发展势头;根据多地地震波序列,可准确定位震源、震级等^[1].有些非时序数据也可经过转化利用时序数据分析方法来处理,如:用树叶的边缘到质心的距离来描述其特征,取不同角度可得到一列数据,进而可判别树叶的类型^[2].

在进行时序数据分析时,如果不考虑数据的时差,则很容易受直觉或偏见的影响,造成相关性的误判;但考虑不相关序列的时差是没有意义的.也就是说,判断序列相关性时需要考虑时差,既要考虑时差又要求数据具有相关性,所以序列之间的相关性和时差相互制约.目前,时序数据相关分析面临一些难题,如数据关系较为复杂、数据中含有噪声、缺失数据或异常数据等^[3].同质数据(来源或属性相同的数据,如多地采集的同一地震的地震波数据)具有天然的相似性,不需要判断相关性,也不存在相关性和时差的制约问题,多用于分类或聚类.而对于异质数据(来源或属性不同的数据,如降水量与河流径流量、CPI和GDP)需要判断其相关性,若具有相关性再做回归分析等.因此,时序数据相关分析的主要对象是异质数据.

与二分类问题或假设检验中的两类错误类似,在对异质数据做相关性分析或数据回归时容易犯两类错误:

(1) 认为相关的数据不具有相关性;

(2) 认为不相关的数据具有相关性并做回归分析.

前者在实际应用中经常出现,比如太阳的仰角与地面温度、降水量与河流径流量,如果按照时间对照研究两组数据的相关性可能得到不相关的结论,但实际上,如果将两者在时间上进行平移,将出现高度相关性.上述第2类错误也会出现,如将过去20年中国的GDP与某人20岁之前的身高做回归,肯定显著正相关,而这其实是没有意义的、不合逻辑的回归,称为伪回归(nonsense regression或spurious regression).因此,在对数据进行分析之前,如果不考虑数据的相关性,第1类相关性错误会造成数据潜在信息的浪费,第2类相关性 错误可能对后续的分析产生误导.多组数据的相关性,可以借助两组数据的相关性来给定.

第1类相关性错误发生的主要原因是两组时序数据发生时间弯曲(time warping),这时只要做时间上的转换,即可实现两者的协同一致.现实中,一般是非线性时间弯曲或动态时间弯曲(dynamic time warping,简称DTW)^[4,5],这就需要借助函数型数据分析(FDA)的方法,将时序数据转化为函数数据做时间校正,一般称为曲线排齐(curve registration)或曲线配准(curve alignment).Kneip和Gasser^[6]将极值等作为特征点排齐(landmark registration),但对于特征点不明显的曲线不大适合,而且特征点的选取对结果影响较大.更一般化的方法是:确定一个目标函数或曲线,将其他曲线的局部特征与之对齐或最小化一些度量(如各曲线与目标曲线的均方距离)^[7].Ramsay等人^[8]提出连续单调排齐方法(continuous monotone registration method,简称CMRM),保证了时间弯曲函数的连续性和一致单调性.Wang与Gasser^[9,10,11]提出一种基于动态时间弯曲模型的曲线排齐方法.Kneip等人^[12]采用关于时间弯曲函数的局部非线性调整方式来排齐曲线.Liu和Müller^[13]在每个观测函数对应于潜在的二维随机过程的框架下,给出相应的随机排齐方法.Rønn^[14],Gervini和Gasser^[15]均采用非参数极大似然法(NPMLE)进行曲线排齐.James^[16]提出基于所有曲线片段等同化的函数对齐方法.Liu和Yang^[17]将曲线排齐和聚类融合起来,并用EM算法求解相应模型,直接得到排齐和聚类结果.较为常见的一种曲线排齐准则是最小化平均曲线误差平方积分(average integrated squared error,简称AISE),其形式为

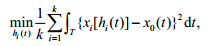
其中,x₀(t)为基准函数,x_i(t)为需要排齐的函数,h_i(t)为各函数对应的时间弯曲函数,k为排齐函数的个数.

以上这些曲线排齐方法多用于处理同质并发数据,但对于异质数据,可能因为量纲不同或负相关而对结果产生不利影响,所以并不适用.目前,关于专门处理异质数据的曲线排齐方法还未见公开报道.

第2类相关性错误(也称伪回归)实际上只是数据上的相关,并非现实的逻辑相关,其研究领域主要集中在计量经济方面.就一般的数据相关性问题,只能从分析伪回归的统计特点加以识别;至于数据在现实中的相关性,还需要根据所选择数据的背景知识去分析.导致伪回归的原因较多,Granger和Newbold^[18]指出:对非平稳时间序列进行回归时,容易产生伪回归现象.但Phillips^[19]研究表明,平稳时间序列也可能出现类似错误.刘汉中^[20,21]对平稳过程的伪回归进行研究,认为残差项未知形式的自相关,是导致伪回归的主要原因,而且残差项往往呈现出与数据过程阶数相同的自相关.一般回归中,如果具有很高的拟合度且具有很低的DW(Durbin- Watson)统计量时,极有可能是伪回归.Jin等人^[22]指出:许多金融时序数据是具有厚尾特征的无限方差序列,此时,DW统计量并非依概率收敛到零.现实数据的复杂多样性加剧了伪回归判断的难度.

同质数据具有天然的相似性,可直接做曲线排齐.对于异质时序数据相关性和时差的相互制约问题,本文固定时差判断各个时移序列的相关性,在序列相关的基础上,再通过曲线排齐细化时差函数.异质数据做相关性判断时,一方面由于样本相关系数与总体相关系数存在偏差,故研究总体相关系数的上下界;另一方面,为防止出现两类相关性错误,从其发生的主要原因出发,研究两类相关性错误的特征并提出相应的相关性判断方法.适用于异质数据的曲线排齐方法同样适用于同质数据,但适用于同质数据的准则(如AISE)并不适用于异质数据(量纲不统一和负相关等).因此,主要根据异质数据的特点提出基于相关系数(绝对值)最大化的曲线排齐准则,并采用S-GEM算法求解.

由于在解决实际问题中只能拿到样本数据,当使用样本估计总体时会产生偏差,因此,本文首先利用样本相关系数推断总体相关系数在一定显著性水平上的界;同时,为防止两类相关性错误的发生,本文研究了两种错误下时移序列相关系数的特征,并据此排除两类相关性错误.综合上述两个方面,可得到两组时序数据的相关性判定方法.

为了判定序列相关性,需要推断总体相关系数的上下界.本文由关于样本相关系数的两个渐近分布得到总体相关系数在一定显著性水平的上下界,然后结合第1类相关性错误的特点,得到具有时间弯曲相关序列的相关性判定方法.

1) 相关系数的界

Pearson相关系数是衡量序列相关性时最常用的度量方式.若有两组对应数据{(x_i,y_i),i=1,2,…,n}(n为样本量)是来自二元正态总体的样本,则样本相关系数为

其中,分别为X,Y的样本均值.

样本相关系数可以作为两个正态总体(X,Y)的相关系数r的无偏和一致估计量,但相关系数有一个明显的缺点,即它接近于1的程度与数据组数n相关,这容易给人一种假象.因为当n较小时,相关系数的波动较大,对有些样本相关系数的绝对值易接近于1,特别是当n=2时,相关系数的绝对值总为1;当n较大时,相关系数的绝对值容易偏小.有不少学者给出关于样本相关系数、样本量和二元正态总体相关系数的分布结果.

在(X,Y)为二元正态总体且p=0的假设下,有如下分布:

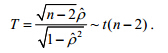
当r=r₀时,Fisher给出了一种较为复杂的的概率密度函数,适当变换后,得到如下渐近分布:

其中,,当样本量较大时,可由样本相关系数对总体相关系数进行估计.

文献^[23]证明了在二元正态总体中抽取n个样本,则有以下渐近分布:

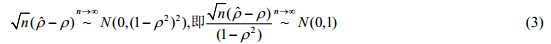
本文分别依据上述两个渐近分布估计总体相关系数.

由于公式(2)中Φ(x)为单调增函数,可知:

·  当时:

·  当时:

其中,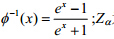为标准正态分布的a分位点,即P(x≤Z_a)=a;随机变量x~N(0,1).

本文在公式(3)的基础上进一步推断总体相关系数的界,即:

·  当时:

·  当时:

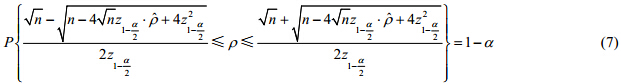
综合公式(4)~公式(7),当a=0.05时,有如下近似:

·  当时:

·  当时:

图 1为在不同样本规模n和样本相关系数下总体相关系数的上下界.从图中可以看出:本文给出的上下界曲线具有以下特点:

(1) 样本规模越大,上下界越紧凑;

(2) 样本规模相同时,上下界曲线中心对称;

(3) 相关系数绝对值越大,上下界越紧凑.

以上特点容易由公式(8)~公式(11)证明.

图 1

Fig. 1

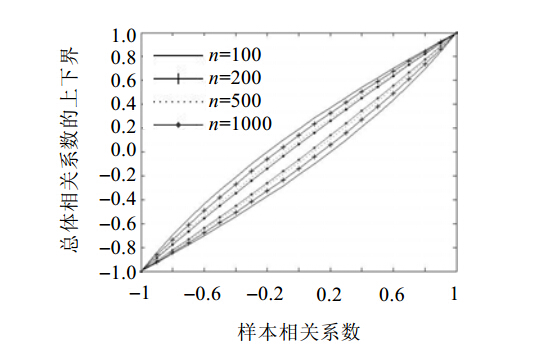Fig. 1 Population correlation coefficient’s bounds (significance level a=0.05)图 1 总体相关系数的界(显著性水平a=0.05)

2) 相关性判定方法

为方便描述序列的相关特征,首先给出时移序列(time-lag series)的定义.

假设两序列(X,Y)={(x_i,y_i),i=1,2,…,n},定义如下序列为时移序列:

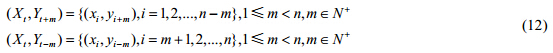
对于第1类回归错误,即认为相关的序列不具有相关性,直接考虑初始序列,其相关性必然较小;如果考虑

其时移序列的相关性,则一定存在m₀(1≤|m₀|<<n,|m₀|ÎN⁺)使得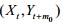的相关系数较大.

由此得到具有时间弯曲相关序列的相关性判定方法:若时移序列的相关系数随m的变化而变化,并在m₀处达到最大值,即曲线图呈现明显的上凸现象,可根据公式(8)~公式(11)估计总体相关系数的范围.如果|r(m₀)|>r₀(即超过给定阈值如0.6),认为时移序列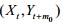存在相关性,可做曲线排齐及回归分析等.

在给出伪回归的相关性判定之前,本文首先研究伪回归的主要原因及其时移序列的相关系数特点,并根据这种特点做出针对性的判断.前面提到,残差项往往呈现出与数据过程阶数相同的自相关,可见,多数情况下伪回归是由残差的自相关性或序列的自相关性引起的.本文分别以序列一阶自相关和残差一阶自相关为前提给出伪回归的相关性判定方法.

(1) 自相关序列的相关性判定

假设两序列(X,Y)={(x_i,y_i),i=1,2,…,n}均是平稳一阶自相关序列,即

其中,a,b,c,d均为常数;和是相互独立的正态随机变量,.

由公式(1)得(X_t,Y_t)的相关系数为

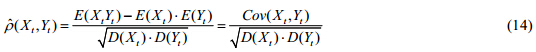
其中,E(×),D(×),Cov(×)分别表示期望、方差和协方差函数.

时移序列(X_t,Y_t+1)的相关系数为

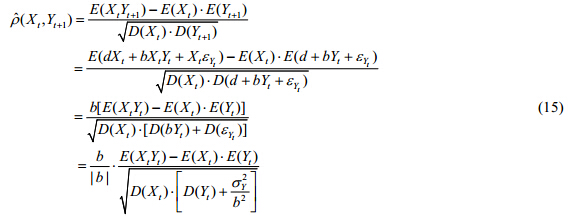
实际问题中,一般b>0,此时,一阶时移序列的相关系数与原序列的相关系数之比为

从公式(16)可以看出:当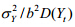较小时,时移序列相关系数与原序列相关系数差异不大;随机项的方差越小,Y_t的方差越大,这种差异越不明显.一般情况下,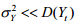,否则,Y_t接近随机序列.因此,一阶自相关序列的时移序列相关系数随m变化不大.

由上述自相关序列的时移序列相关系数特点得到如下伪回归相关性判别方法:假设时间序列(X_t,Y_t)的时移

序列为(X_t,Y_t+m),其相关系数随m的改变无明显变化(如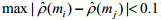),则认为两序列无相关性.即便其相关系数很高,做出的回归也是伪回归.

(2) 残差自相关序列的相关性判定

假设两序列(X,Y)={(x_i,y_i),i=1,2,…,n}的回归模型如下:

其中,q为常数;残差序列e_t一阶自相关,即

其中,c为残差序列自相关系数;m_t为白噪声序列,且

由公式(17)、公式(18)可得E(Y_t+1-Y_t)=cq×E(X_t+1-X_t),根据归纳法知E(Y_t+m-Y_t)=(cq)^m×E(X_t+m-X_t),当然有:

若令故有:

如果X_t具有自相关性,则也有自相关性,设为,则:

.

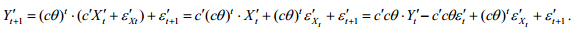即:

.

上述推导表明:当残差序列一阶自相关时,若有一个序列一阶自相关,则另外一个序列也必定一阶自相关.这与文献^[21]中的结论“如果数据过程的生成机制都是自回归模型时,随机干扰项往往呈现出与数据过程阶数相同的自相关”相吻合.由自相关序列的特点知,残差自相关序列的时移序列相关系数对m的变化不敏感,因此,残差自相关序列的相关性判定方法可参照自相关序列的相关性判定方法.

由第1.1.1节和第1.1.2节的分析,本文关于相关性判定方法可总结如下:

1) 如果时移序列的相关系数都比较小,则两序列无相关性或相关性不明显;

2) 如果时移序列的相关系数都比较大,但变化不明显,则两序列无相关性或相关性不明显,即出现伪回归现象;

3) 如果时移序列的相关系数出现明显上凸现象(正相关),且在极值点处总体相关系数(由样本相关系数推断)比较大,则两序列为具有时间弯曲的相关序列.

通过时移序列的相关系数,可以判定序列间是否具有相关性.若两序列存在相关性,但具有时间偏差,就需要曲线排齐方法将其对齐,消除相位上(时间轴上)的差异.对于异质数据,当采用AISE准则时,其结果会随量纲变化而变化,因此,需要提出一种无量纲的准则来排齐异质数据组成的曲线.

Pearson相关系数是一种描述两序列相关性或相似性的无量纲度量方式,但仅适用于描述离散数据的相关性.连续函数的相关性可用内积表示,同时,为使内积取值规范化,再除以两个函数的范数.异质数据组成的曲线排齐准则可通过函数型相关系数来构建:

其中,表示排齐后的函数.鉴于连续型函数的运算复杂性以及优化准则的高维特征,本文给出对应

的离散化形式.

假设两个函数型数据x₁(t)和x₂(t)在采样时间点T=(t₁,t₂,…,t_n)处的样本序列为x₁(T)=[x₁(t₁),x₁(t₂),…,x₁(t_n)]和x₂(T)=[x₂(t₁),x₂(t₂),…,x₂(t_n)],现要将函数x₁(t)对照x₂(t)做曲线排齐.令Δ=(d₁,d₂,…,d_n)为在时间点T处x₁(t)相对于x₂(t)的偏移量,即时间弯曲函数满足h(T)=T+Δ,则经过排齐的时序样本变为x₁(T+Δ)=[x₁(t₁+d₁),…,x₁(t_n+d_n)],排齐后的两组函数型数据的样本序列应当具有较高的相关性.曲线排齐问题可转化为求解:

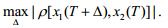
一般时间弯曲函数具有一致单调性,即满足t_i-1+d_i-1<t_i+d_i<t_i+1+d_i+1.然而,偏移向量杂乱无序会造成时间弯

曲函数不满足一致单调性,故限定,其中,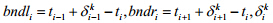,表示第k次迭代时d_i的值.具体实现时,可将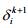的搜索区间缩小为闭区间[bndl_i+p×(bndr_i-bndl_i),bndr_i-p×(bndr_i-bndl_i)],其

中,p为(0,0.5)内的常数.

最终,曲线排齐问题变为求解下面的约束优化问题:

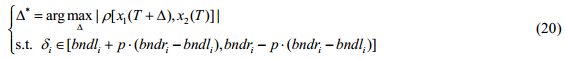
最后,将时间偏移向量Δ转化为函数形式,得到时间偏移函数d(t),相应的时间弯曲函数为h(t)=d(t)+t.

文献^[1,17]中采用EM算法求解曲线排齐优化问题,但当参数的维数较高时,难以求解Q函数的极大化问题.为克服此问题,本文将问题(20)的目标函数作为Q函数(即EM算法中对数似然函数的期望),将推广的EM算法(广义期望最大化算法GEM)用于求解式(20);由于时间弯曲函数和时间偏移函数具有较好的光滑性,为加快其收敛速度,每进行完一次Δ的更新,都做一次P样条光滑处理,以增强时差向量的光滑性,而且P样条具有正则项,可防止过度优化造成的时差函数不稳定问题.因此得到求解模型(20)的光滑广义期望最大化方法(S-GEM),其主要步骤如下:

输入:两组在时间T₀=(t₀₁,t₀₂,…,t_0m)上具有时间弯曲的相关时序数据TS₁,TS₂;

Step 1. 初始化时差向量Δ₀=zeros(1,n),迭代容许误差eps.

Step 2. 时序数据函数化.将TS₁,TS₂转化为函数型数据x₁(t)和x₂(t),并在T₀内均匀取n个点T=(t₁,t₂,…,t_n),

得到光滑序列{x₁(t_i)}和{x₂(t_i)}(i=1,2,…,n),其中,t₁=t₀₁,t_n=t_0m.

Step 3. 用广义期望最大化求时差向量.记第k次迭代时差向量为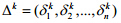,进行n-2次条件极大化(假定起始点无时差,即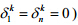),得到.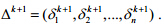

Step 4. 时差向量的光滑处理:采用P样条拟合关于序列Δ^k+1的函数d^k+1(t),并将拟合值替代原始值,即:

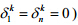
Step 5. 重复Step 3和Step 4,直到收敛(|Δ^k+1-Δ^k|<eps).

输出:时差函数d(t)=d^K(t)或时间弯曲函数h(t)=d(t)+t.

与很多函数型数据分析方法类似,本文提出的算法可处理数据量较大的数据排齐问题,即使存在数据缺失或异常数据,也能充分利用当前信息;另外,算法经过光滑处理,能够快速收敛到极值.重要的是,算法的运行时间或时间复杂度主要依赖于抽样个数,而与原始样本个数无关.S-GEM算法的复杂度分析见表 1.

表 1(Table 1)

Table 1 Complexity of S-GEM algorithm 表 1 S-GEM算法的复杂度分析 步骤 时间复杂度 空间复杂度 Step 1 O(n) O(n) Step 2 函数化: O[(m+d-2)3] 取值: O(nd2) 函数化: O[(m+d-2)2] 取值: O(n) Step 3 O[nxfm] O(n) Step 4 光滑: O[(n+d-2)3] 取值: O(nd2) 光滑: O[(n+d-2)2] 取值: O(n) 总体 O[(m+d-2)3+k((n+d-2)3+nxfm)] O[(m+d-2)2+(n+d-2)2]

Table 1 Complexity of S-GEM algorithm 表 1 S-GEM算法的复杂度分析

其中,m为初始样本量,n为均匀采样量,d为函数化的阶数(最高次数减1),fm为Step 3中条件极大化的平均时间复杂度,k为总体迭代次数.由于fm和k与精度、参数和问题本身有关,故将其单独设出.数据函数化或光滑时采用P样条,样条函数的系数向量估计时最复杂的部分在样条基函数矩阵求逆,时间复杂度和空间复杂度分别为基函数个数的3次和2次.一般,m³为有限计算量,相对于迭代过程可略去;d取值较小,本文实验中d=4,此时算法时间复杂度和空间复杂度分别为O[k(n³+nxfm)]和O[m²+n²].

本文在模拟数据(7种人造时序数据和两组Sinc函数)和真实数据(先行指数与一致指数,GDP与城镇就业人数、城镇居民家庭人均可支配收入)上对所提出的相关性判定方法及曲线排齐方法进行验证.对于上述存在时间弯曲的相关数据,采用本文方法做了曲线排齐,一方面分析方法对参数的敏感性,另一方面与已有方法进行对比分析.

(1) 伪回归判定

关于伪回归判定问题,选择时序数据的7种主要数据产生过程(data generating process,简称DGP)(见表 2),分别通过时移序列的相关系数来判别伪回归,表 3为伪回归检测中设置的参数值.

表 2(Table 2)

Table 2 Data generating process 表 2 数据产生过程 模型序号 名称 模型 1 AR(1): (无漂移)一阶自回归 2 AR(1)+Drift: 带漂移一阶自回归 3 I(1): (无漂移)一阶单整 模型序号 名称 模型 4 I(1)+Drift: 带漂移一阶单整 5 IMA(1,1): 一阶单整移动平均 6 ARMA(1,1): 自回归移动平均(1,1) 7 ARMA(2,2): 自回归移动平均(2,2)

Table 2 Data generating process 表 2 数据产生过程

表 3(Table 3)

Table 3 Parameters in spurious regression detection 表 3 伪回归检测中设置的参数值 模型 变量 a1 a2 c u1 u1 s2 1 Xt 1 1 Yt 1.01 1 2 Xt 0.98 5 1 Yt 1 3 9 3 Xt 1 1 Yt 1 1 4 Xt 1 2 25 Yt 1 1 25 5 Xt 1 0.5 1 Yt 1 0.5 1 6 Xt 1.05 0.2 1 Yt 1.01 0.2 1 7 Xt 0.5 0.5 1 1 1 Yt 0.3 0.7 0.5 2 1

Table 3 Parameters in spurious regression detection 表 3 伪回归检测中设置的参数值

首先采用常规相关性判别方法分析上述7组序列的相关性,其结果为表 4和表 5.

表 4(Table 4)

Table 4 Correlation coefficients of series with different models 表 4 各模型序列的相关系数 模型 Pearson线性相关系数 Spearman秩相关系数 Kendall秩相关系数 1 -0.877 -0.811 -0.598 2 0.861 0.997 0.961 3 0.060 0.000 0.012 4 0.922 0.950 0.821 5 0.046 -0.014 0.005 6 0.893 0.951 0.849 7 0.828 0.987 0.940

Table 4 Correlation coefficients of series with different models 表 4 各模型序列的相关系数

表 5(Table 5)

Table 5 Granger causality test of series with different models 表 5 各模型序列的Granger因果检验 模型 单整阶数 Granger因果检验(Lag=0) X Y 因®果 F统计量 显著性 是否Granger原因 1 1 1 Y®X 0.006 0.993 否 X®Y 0.287 0.750 否 2 0 1 Y®X 1.185 0.307 否 X®Y 0.019 0.980 否 3 1 1 Y®X 0.412 0.662 否 X®Y 0.129 0.878 否 4 1 1 Y®X 0.412 0.662 否 X®Y 0.129 0.878 否 5 1 1 Y®X 0.513 0.599 否 X®Y 0.164 0.848 否 6 4 1 Y®X 6.463 0.002 是 X®Y 1.799 0.168 否 7 4 1 Y®X 4.035 0.019 是 X®Y 16.653 0.000 是

Table 5 Granger causality test of series with different models 表 5 各模型序列的Granger因果检验

由表 4可见:模型3和模型5的相关系数比较小,不会出现伪回归现象.其他各组自相关序列的3种相关系数均比较高,表明常规相关系数对于自相关序列的伪回归现象不具有鉴别能力.由表 5可见:Granger因果检验能够识别多数序列的相关性,但仍有3处识别错误.其中,模型7为二阶自相关序列,双向Granger因果检验均错误.因此对于简单模型,Granger因果检验能识别伪回归;当模型较复杂时,不能识别伪回归.

由于上述3种相关系数和Granger因果检验均不能较好地判别自相关序列的相关性,后续实验中不再使用这些方法判别相关性.

图 2为7种模型的时移序列相关系数变化图.由图 2可见:模型3和模型5的时移序列相关系数绝对值较小,不会造成伪回归.其他5个模型的相关系数较高,但时移序列的相关系数随m变化不大,采用本文方法可以快速准确地识别伪回归.虽然本文给出一阶自相关序列的伪回归判别方法,但由模型7的结果可见:对于二阶自相关序列,同样能够得到可靠的相关性判定结果.

图 2

Fig. 2

Fig. 2 Correlation coefficients in time-lag series图 2 时移序列相关系数变化图

(2) 时间弯曲序列相关性判定

选择具有波动性的Sinc函数(Sinc(x)=sinpx/px,xÎ^[-6,6])作为模拟数据相关性研究对象,并且做如下两种时差函数:d₁(t)=0.01t²-0.36,d₂(t)=0.005t(t-6)(t+6).两种情况下,与标准Sinc函数及时移序列相关系数变化趋势如图 3所示.

图 3

Fig. 3

Fig. 3 Sinc functions and correlation coefficients in their time-lag series图 3 Sinc函数和时移序列相关系数变化图

从图 3(b)中可以看出:两条时移序列相关系数曲线都有明显的上凸现象,且两个相关系数的界分别为[0.991,0.996]和[0.914,0.962].由此可判定两组序列存在相关性,且时差函数分别为d₁(t)和d₂(t)的序列与标准Sinc函数序列的平均滞后量分别为0和3.

(1) GDP与城镇就业人数、城镇居民家庭人均可支配收入

本文收集了1980年~2011年国家统计局公布的年度数据^[24]:国内生产总值(GDP/亿元)、城镇就业人数(万人)、城镇居民家庭人均可支配收入(简称可支配收入/元).两两之间时移序列的相关性如图 4所示.

图 4

Fig. 4

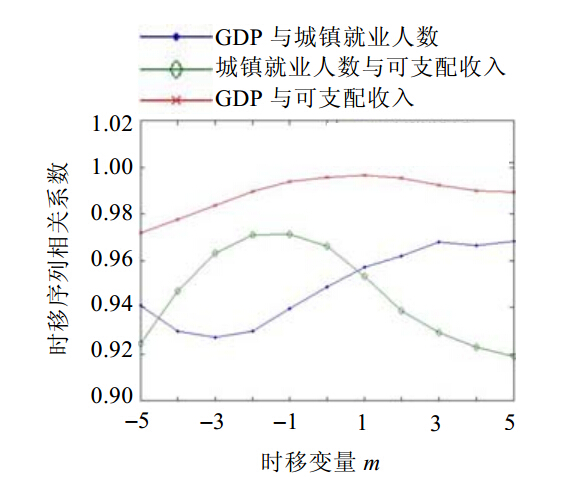Fig. 4 Correlation coefficients in time-lag series图 4 时移序列相关系数变化图

由图 4可见:GDP与城镇就业人数、GDP与可支配收入之间的相关系数很高,但其时移序列相关系数变化不大,故GDP与城镇就业人数及可支配收入无相关性;而城镇就业人数与可支配收入相关系数很高,在m=-1处达到最大值0.97,并且估计得到相关系数的界为[0.85,0.98],符合上凸条件且相关性较大,故判定两者存在相关性,且城镇就业人数平均比可支配收入滞后一期(一年).这一结果与大多数“就业水平与人均收入存在动态均衡关系”的结论是一致的,并且说明收入的增加能带动就业人数的增长.

(2) 先行指数与一致指数

本文选择的2008年~2011年期间先行指数与一致指数的月度数据同样来自文献^[24].由于先行指数和一致指数分别由不同的经济指标合成,因此两者属于异质数据.图 5为两个指数及时移序列相关系数变化图.从图 5(b)中可以看出:时移序列相关系数曲线有明显的上凸现象,在m=4处达到最大值0.82,并且估计得到相关系数的界为[0.655,0.883],故判定两组序列存在相关性,且一致指数平均比先行指数滞后4个月.中国经济景气监测中心指出,2004年3月先行指数领先3个月.本文结果表明:受金融危机影响,2008年~2011年期间,先行指数的平均领先期数略微增大.

图 5

Fig. 5

Fig. 5 Leading index,coincident index and correlation coefficients in their time-lag series图 5 先行指数与一致指数及时移序列相关系数变化图

本节主要对S-GEM算法的性能进行测试,并与经典的CMRM算法^[8]、极大似然排齐(maximum likelihood registration,简称MLR)^[15]和自模型排齐(self-modeling registration,简称SMR)^[25]进行比较.为公平起见,CMRM算法和MLR的结果为5次运行的平均结果.实验的机器配置为:Intel四核CPU(主频为2.83GHz),3G内存.

将时差函数分别为d₁(t)=0.01t²-0.36和d₂(t)=0.005t(t-6)(t+6)的含噪声的Sinc函数与标准Sinc函数做曲线排齐.在两种时差函数下,4种排齐方法经过调参后的排齐效果如图 6所示.

图 6

Fig. 6

Fig. 6 Registration results of 4 methods图 6 4种方法的排齐结果

由图 6可见:时差函数为d₁(t)时,MLR排齐效果较差,其他3种比较接近实际值;时差函数为d₂(t)时,MLR和CMRM排齐效果较差,SMR和S-GEM非常接近时差函数.

表 6~表 9为Sinc函数在两种时差函数下分别采用CMRM,MLR,SMR,S-GEM的排齐结果.

表 6(Table 6)

Table 6 Registration results of Sinc function by CMRM (5 times on average) 表 6 Sinc函数CMRM排齐结果(5次平均) 时差函数 运行时间(s) RMSE d1(t) 20.32 0.003 8 d2(t) 30.74 0.089 1

Table 6 Registration results of Sinc function by CMRM (5 times on average) 表 6 Sinc函数CMRM排齐结果(5次平均)

表 7(Table 7)

Table 7 Registration results of Sinc function by MLR (5 times on average) 表 7 Sinc函数MLR排齐结果(5次平均) 时差函数 参数 运行时间(s) RMSE 尺度参数 最大迭代次数 d1(t) 0.1 50 14.60 0.108 6 0.1 100 22.24 0.146 2 d2(t) 0.1 50 14.51 0.150 4 0.1 100 21.83 0.133 7

Table 7 Registration results of Sinc function by MLR (5 times on average) 表 7 Sinc函数MLR排齐结果(5次平均)

表 8(Table 8)

Table 8 Registration results of Sinc function by SMR 表 8 Sinc函数SMR排齐结果 时差函数 实验序号 参数 运行时间(s) RMSE 成分个数 基函数个数 d1(t) 1 4 7 5.49 0.060 6 2 3 8 6.87 0.011 8 3 3 8 6.05 0.013 3 4 4 7 5.65 0.063 2 5 3 7 6.27 0.051 2 平均 3.4 7.4 6.06 0.040 0 d2(t) 1 4 12 21.99 0.020 8 2 4 11 25.10 0.047 4 3 5 13 24.56 0.067 4 4 4 12 23.82 0.061 1 5 4 15 23.00 0.088 8 平均 4.2 12.6 23.69 0.057 1

Table 8 Registration results of Sinc function by SMR 表 8 Sinc函数SMR排齐结果

从表 9中可以看出:总体上,S-GEM算法的精度主要与采样点数密切相关,而且时差函数越复杂,需要的采样点数越多;S-GEM算法的运行时间主要随采样点数的增加而变长.

表 9(Table 9)

Table 9 Registration results of Sinc function by S-GEM 表 9 Sinc函数S-GEM算法的排齐结果 时差函数 迭代误差eps 采样点数n 运行时间(s) RMSE d1(t) 0.01 10 0.15 0.261 8 30 4.29 0.029 3 50 7.76 0.011 9 80 16.52 0.013 5 100 25.47 0.016 9 0.05 10 1.13 0.083 5 30 3.2 0.018 0 50 7.96 0.012 0 80 17.15 0.023 9 100 24.87 0.024 5 0.1 10 0.15 0.261 8 30 3.13 0.030 1 50 7.33 0.019 1 80 15.19 0.023 2 100 19.72 0.029 8 d2(t) 0.01 10 0.15 0.296 9 30 4.74 0.035 6 50 8.04 0.029 7 80 16.61 0.026 9 100 27.82 0.034 0 0.05 10 0.15 0.296 9 30 4.09 0.033 7 50 8.15 0.022 4 80 16.78 0.026 1 100 22.75 0.028 8 0.1 10 0.15 0.296 9 30 3.31 0.037 9 50 7.09 0.032 4 80 14.73 0.026 5 100 20.60 0.037 4

Table 9 Registration results of Sinc function by S-GEM 表 9 Sinc函数S-GEM算法的排齐结果

对比表 6~表 9的结果可见:

·  时差函数为d₁(t)时,CMRM精度最高,但效率最差;SMR和S-GEM的精度和效率都差不多,但SMR结果不如S-GEM稳定;MLR的精度最差,效率不高;

·  时差函数取d₂(t)时,SMR和S-GEM精度较高,但SMR效率远不及S-GEM,而且不如S-GEM稳定.

以上实验表明:对于简单的时差函数,CMRM,SMR和S-GEM的精度都比较高,但CMRM效率较差;当时差函数较复杂时,SMR和S-GEM排齐结果较好,但在效率和稳定性上SMR不如S-GEM.

表 10(Table 10)

Table 10 Curve registration results of leading index and coincident index 表 10 先行指数与一致指数排齐结果 方法 采样点数n 迭代误差eps 运行时间(s) 相关系数 S-GEM 20 0.1 6.32 0.980 5 0.2 6.35 0.980 5 0.3 6.40 0.980 5 0.4 16.22 0.980 8 0.5 18.16 0.980 9 30 0.1 9.27 0.999 5 0.2 9.04 0.999 5 0.3 8.32 0.999 5 0.4 8.01 0.999 5 0.5 7.88 0.999 5 40 0.1 16.96 0.999 4 0.2 15.47 0.999 5 0.3 15.86 0.999 5 0.4 15.47 0.999 5 0.5 15.33 0.999 5 CMRM (5次平均) 32.31 0.943 5 SMR (5次平均) 11.77 0.873 9 MLR (5次平均) 3.78 0.856 6

Table 10 Curve registration results of leading index and coincident index 表 10 先行指数与一致指数排齐结果

表 10为先行指数对照一致指数做曲线排齐的结果.由于真实的时差函数未知,对于真实数据,采用相关系数比较两种方法的效果.由表 10可见,S-GEM算法主要对采样点数敏感.即采样点过少,效果变差,但相关系数仍比其余3种方法要大;采样点过多,运算量大,但S-GEM算法无论从结果还是效率上都优于CMRM算法.SMR和MLR虽然运行时间短,但相关系数较小.

图 7为S-GEM算法(n=30,eps=0.3)与其他3种方法的排齐效果.为方便观察,图中给出了4个极值点处的虚线.可以观察到:在第2个极值点处,只有MLR不能对齐;在第1、第3极值点处,SMR和MLR稍逊于S-GEM和CMRM;在第4个极值点处,只有S-GEM能够对齐.

图 7

Fig. 7

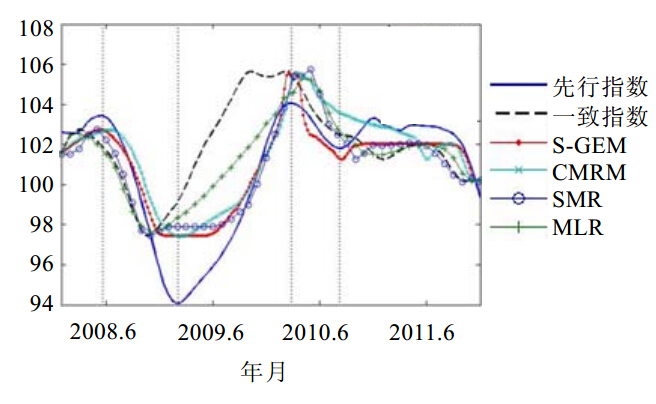Fig. 7 Comparison of registration results图 7 排齐结果比较

总之,在先行指数对照一致指数的排齐过程中,相比于CMRM,SMR和MLR,S-GEM算法在排齐效果(相关系数和直观图形)上均优于其他方法,且运算效率高于CMRM和SMR.

本文在一定显著性水平上给出总体相关系数的上下界,并用于判别相关性.伪回归问题产生的原因较多,目前尚未找到严格、准确的识别方法.本文从伪回归产生的主要原因出发,得到关于时移序列相关系数的特点,能够排除多数常见的伪回归现象;对于另外一种相关性错误,可从时移序列相关系数的特征认定其相关性.对存在时间弯曲的相关序列,建立了基于相关系数最大化的模型和改进的S-GEM求解算法,模型的适用范围比AISE准则更广.实验结果表明,本文的相关性判别方法在伪回归识别中比Pearson线性相关系数、Spearman秩相关系数、Kendall秩相关系数以及Granger因果检验更有效.提出的S-GEM算法在大多数情况下明显优于CMRM,SMR和MLR.本文考虑的是双序列的线性相关问题和函数型曲线排齐方法,这些结果可为回归分析的相关性判定和时间对齐提供理论基础,并为多序列相关性分析和曲线排齐提供参考方向.

对于具有一定光滑性的高维数据,可以将其转化为函数型数据进行分类、回归、聚类等分析;另一方面,也可以采用各个基函数的系数对高维数据进行降维.本文提出的函数型相关系数和曲线排齐方法可为高维数据的回归、聚类等做好相关性度量以及降维等前期工作.

函数型数据的光滑技术便于处理数据量比较大的时序数据,在一定程度上能够克服数据含噪声、数据缺失和数据异常的问题,本文进一步将其用于加速曲线排齐迭代算法.然而,S-GEM算法的采样点数直接影响排齐效果和排齐时间,因此,如何根据排齐问题确定最佳采样点(数量和位置),也是今后研究的一个重要方向.