2. 清华大学 计算机科学与技术系, 北京 100084
2. Department of Computer Science and Technology, Tsinghua University, Beijing 100084, China
随着物联网技术的不断成熟,有越来越多的行业开始利用物联网进行远程实时监测.如图 1所示,将无线传感器网络技术、移动通信技术、WiFi技术、嵌入式技术、北斗短信通信技术、智能信息处理技术等技术应用于三江源生态监测,既能获取到监测区域的实时信息,又能实现监测目标的可视化,是环境监测技术的一次变革.然而对于计算资源、存储资源、能量和带宽都很有限的物联网感知部分来说,可靠性是制约其实用化的最大因素,而且监测区域偏远、基础通信环境差导致的主干传输信号弱,也会给监测系统的可靠性带来重大影响.
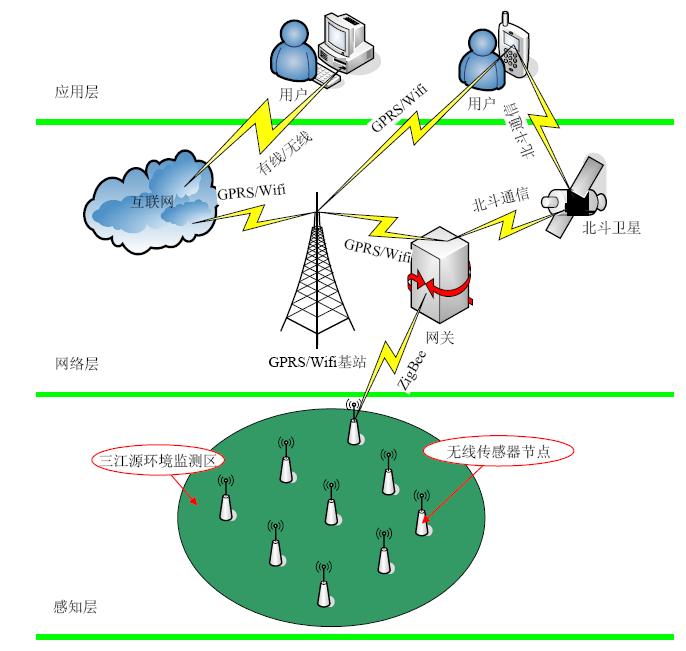 | Fig. 1 Framework of IoT-based remote real-time monitoring system图 1 基于物联网的远程实时监测系统整体架构 |
本文的贡献如下:① 以基于物联网的三江源远程生态环境监测为背景,提出了一种适合三江源等偏远环境的物联网拓扑部署与保障可靠性的设计方法,对设置无线传感器网络的拓扑结构层数、监测面积和监测节点数等参数的相互关系给出了量化的计算公式;② 针对三江源偏远恶劣监测环境,提出了一种保障监测区域和远程主干传输拓扑可靠的有效机制及量化分析方法;③ 在考虑传感器节点费用的基础上,提出了一种提高簇头节点和协调器拓扑可靠性的动态优化策略和方法.
1 相关工作节点部署是利用无线传感器网络进行监测的基础,只有把传感器节点在监测区域布置好,才能进一步进行其他的工作和优化[1].节点的部署方式通常分为随机抛撒、确定性部署和网格部署[2,3,4].随机抛撒适合应用于某些特殊场合,如战场中的侦查任务、灾难恢复和森林火灾探测等,其应用环境通常非常恶劣,无法进行人为安装与配置节点.但是,随机抛撒是不考虑服务质量(quality of service,简称QoS)的盲目部署,只能用冗余换取性能保证[5],且随机抛撒费用较高.确定性部署是将传感器节点放置到指定的区域,这种部署方式适合小规模应用,且不同的应用其部署方式也不一样[4].网格部署是通过相交的线段将监测区域划分为不同的网格,传感器节点部署在两条(或多条)线段的交点处.实现全对称的网格部署有三角形网格部署、正方形网格部署和六边形网格部 署[6].严格意义上讲,网格部署也是确定性部署的一种,但网格部署既能保障网络的覆盖度和连通性,又具有简单、易扩展等特性,因此有很多学者对其进行研究,如文献[4,6,7,8,9].文献[6]针对对称格型传感器网络的可靠性进行了建模和分析,指出节点间距在60m~100m时,节点间距变化对节点平均可靠性影响最小,并且在这个间距范围内,三角形和六边形节点部署方案较好.文献[8]对应用于大规模无线传感器网络的均匀随机部署、正方形网格部署、三角形-六边形拼接(tri-hexagon tiling,简称THT)部署在覆盖、能耗、传输延迟等性能指标上进行了分析,指出:正方形网格部署在覆盖范围上比其他两种部署方式要好,在能耗和最坏传输延迟上,THT要优于其他两种部署方式.但文献[6,8]在对传感器网络进行建模时并未考虑传感器网络的分簇结构.
簇结构在无线传感器网络中是一种广泛应用的拓扑结构,因为簇结构可以进行有效的数据聚合,进而减少节点转发数据包的数量,从而减少能耗,延长网络的寿命.在簇结构中,节点类型分为普通叶节点和簇头节点:普通叶节点仅仅感知信息;簇头节点既要感知信息,又要收集、处理和转发其他节点的信息,并将它们传送到Sink节点[10].文献[11]给出了一种确定每个簇中节点个数、簇头选择方案及簇中节点位置信息的方法.该方法既不需要昂贵的定位设备, 又能节省能量.文献[12]将第1个簇头节点能量耗尽的时间定义为覆盖时间,进而研究通过在不同簇头节点之间平衡能耗使覆盖时间最大化.对于簇间通信,文献[12]通过使用瑞利衰减信道模型提供最佳能量分配策略来保障(簇头之间)端到端路径可靠性的上界,而且提出了两种平衡能耗的机制:已知路由的最优簇规划和已知簇的最优随机转发机制.通过以上两种机制,将能耗均衡问题归结为符号优化问题,进而通过广义几何规划方法进行解决.在数据采集方面,文献[13,14]提出了可移动Sink节点的数据收集方式,移动Sink节点收集数据在一定程度上节省了簇头节点的能量,降低了能耗,延长了网络寿命.
在无线传感器网络实际应用时,投资费用是一个重点考虑的问题.因此,在探究传感器节点部署时,除了考虑覆盖度、连通性、耗能等度量以外,投资费用也是一个约束条件.文献[7]在分布式传感器网络中,利用网格覆盖对目标进行监控和定位.针对感知区域全覆盖所需的最少传感器数量问题,首次提出了一种整数规划方案.文献[15]提出了一种多目标部署算法(multi-objective deployment algorithm,简称MODA).MODA首次将部署费用、事件探测概率、网络连通性、能耗等同时作为约束条件进行优化部署,由于多目标组合优化问题是一个NP难问题[16],且对大面积节点部署来说,寻求帕斯托边界最优解序列是困难的,因此,MODA将进化算法和邻居搜索算法相结合获得近似最优解.但文献[15]将网络寿命定义为“所有传感器均不能与Sink节点通信”,没有考虑失效节点数与监测信息准确度的关系.
在数据传输过程中,为了确保可靠性,往往采取重传或者冗余.文献[17]对无线传感器网络中的重传和冗余机制进行了量化评估,指出:当丢失率保持在较低或者中等水平时,采取纠删码(一种冗余机制)比采取重传更节能;但是在跳数增加或者在丢失率高的情况下,冗余机制的优势将会减弱.由此,文献[17]以丢失探查和丢失恢复为基础,提出了两种改进纠删码机制.在实际信道 中,丢失恢复的纠删码不仅更节能,而且与重传具有同等水平的可靠性.
2 远程监测中基于均匀分簇的物联网拓扑层次结构与量化分析 2.1 均匀分簇的可扩展的模块化节点部署方法在无线传感器网络中,如何设计节点间的逻辑结构来延长网络的寿命、提高网络的可扩展性,是节点部署过程中需要重点研究的问题之一.为了适应三江源这类大面积环境监测的需求,本文采用一种模块化的均匀分簇的星型混合分层结构来保证网络拓扑的可靠性、网络的可扩展性以及数据融合的均衡性.
定义1(基本监测区域BA). 基本监测区域BA是如图 2(a)所示的由9个前后左右等距离、分布均匀的监测点组成的正方形监测区域,其中,四周的8个白色节点是只进行监测的叶节点,不进行数据的转发.BA正中间的节点与其他8个叶节点的距离基本相近,带有路由的性质,既监测数据又转发自己和叶节点的数据,充当簇头的角色.
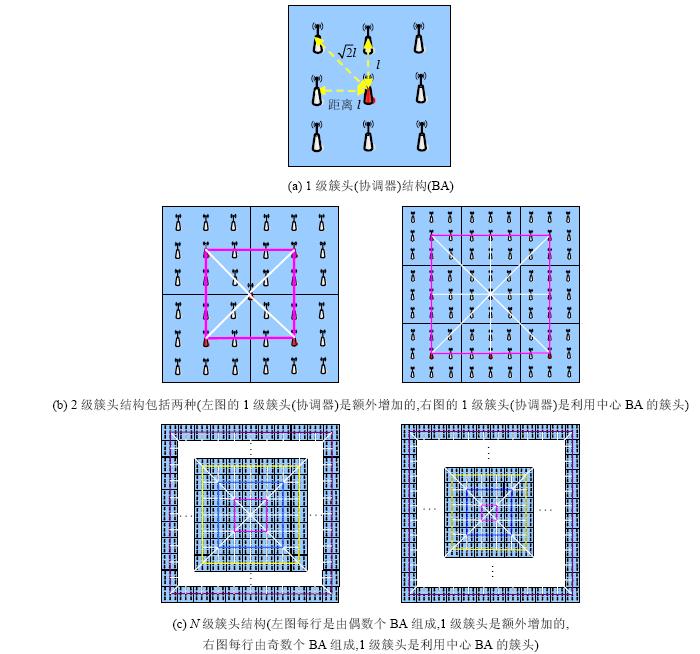 | Fig. 2 Several classical topology structure of monitoring region图 2 几种典型的监测区域拓扑结构 |
定义2(理想监测区域IA). 理想监测区域IA是指未考虑监测节点冗余而只考虑节点有效传输半径的最大监测覆盖区域.
定义3(一般监测区域GA). 一般监测区域GA是指实际需要监测的区域.如果其监测的面积小于BA的面积,就用BA作为监测区域,并通过调节节点间的距离l来达到与实际面积相等的目的;如果GA的面积大于BA的面积,就使用BA进行模块化组合,并保持正方形拓扑结构不变.
在本文中,IA与GA是由模块化的BA组合而成.在每个BA中,节点分布均匀有利于数据准确的融合,且在BA中,簇头节点与其他节点距离基本相等有利于传输数据的能耗均等.
监测区域(BA,IA或GA)的节点部署采用簇结构,如图 2(a)~2(c)所示,整个监测区域有唯一的一个管理和配置网络的协调器节点(当监测区域中心有BA时,BA的簇头兼作协调器,当中心没有BA时,另外单独增加节点作为协调器)担当Sink节点,并与监测区域的网关进行通信.将协调器作为1级簇头节点,离协调器最近的一周带路由功能的节点作为2级簇头节点,依次向外为3级簇头节点,…,n级簇头节点(n级簇头节点对应的拓扑结构层数n¢为n+1).
实际应用时,根据监测区域面积的大小将基本区域BA进行组合,使整个监测区域中的传感器节点具有层次结构.例如,当布置3层结构的监测区域,即拓扑结构的层数为3(如图 2(b)所示)时,为了仍保持正方形拓扑结构,使用4块或者9块基本区域BA进行组合.n级簇头结构的监测区域如图 2(c)所示,图中的白线代表数据流方向,每个r级簇头节点(r≤n)都将自己的数据传送给离它最近的r-1级簇头节点.
2.2 拓扑结构相关参数的计算与分析定理1. 设传感器的传输半径为D,理想监测区域IA的面积为s,则拓扑结构的层数n¢为
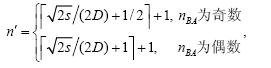
其中,nBA是组成IA横向/竖向基本监测区域的BA个数.
证明:设BA中各个节点间的最大水平(垂直)距离为l,叶节点到簇头节点以及簇头节点间的距离分以下几种情况:
1) 叶节点到本BA中的簇头节点的距离有两种(如图 2(a)所示):① 水平/垂直距离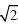 l;② 对角线距离3
l;② 对角线距离3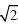 l(2≤r≤n).
l(2≤r≤n).
2) r级簇头节点到r-1级簇头节点的距离有两种:① 水平或者垂直距离3l;② 对角线距离3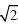 l(2≤r≤n).
l(2≤r≤n).
3) 如果监测中心没有中心BA,则需要单独增加协调器(一级簇头节点),它和二级簇头节点连线形成对角线,其距离为(3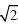 /2)l.
/2)l.
因此,任意两个节点直接传输信息的最远距离D要大于等于以上5个值中的最大者.在本文中,我们假设D取以上5个值中的最大者,即

因为正方形IA的面积为s,边长为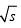 ,所以每行节点数m为[
,所以每行节点数m为[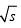 /l]将公式(1)代入m=[
/l]将公式(1)代入m=[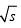 /l]可得:
/l]可得:
m=[3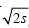 /D]
/D]
由于BA每行有3个节点,所以组成IA横向/竖向基本监测区域BA的个数nBA=[2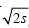 /D/]当组成IA横向/竖向的BA个数为偶数时,需要另外单独增加一个协调器(一级簇头节点);而当为奇数时,直接使用中间BA的簇头节点兼做协调器.因此,将nBA分为奇数和偶数分别进行论述:
/D/]当组成IA横向/竖向的BA个数为偶数时,需要另外单独增加一个协调器(一级簇头节点);而当为奇数时,直接使用中间BA的簇头节点兼做协调器.因此,将nBA分为奇数和偶数分别进行论述:
(1) 当nBA为奇数且1<r≤n时,根据图 2所示的拓扑结构,有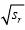 =
=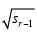 +2×3l由公式(2)计算得到r级簇头结构对应的理想监测面积sr为公式(3):
+2×3l由公式(2)计算得到r级簇头结构对应的理想监测面积sr为公式(3):


当r=1时,sr符合公式(3).
当r=n时,sr=sn=s,联立公式(1)和公式(3)可得:

解方程组(4)得到簇头级数n=[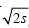 /(2D)+1/2]加上普通叶节点那一层,得到拓扑结构的层数n'为
/(2D)+1/2]加上普通叶节点那一层,得到拓扑结构的层数n'为
n'=[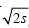 /(2D)+1/2] +1
/(2D)+1/2] +1
(2) 当nBA为偶数时,由于拓扑层次数最小为2,因此根据公式(5):

计算得到r级簇头节点对应的理想监测面积sr为

当r=n时,sr=sn=s,将公式(1)代入公式(6)可得:

加上普通叶节点的那一层,得到拓扑结构的层数n¢为n'=[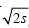 /(2D)+1] +1
/(2D)+1] +1
综上所述,

性质1. 设每行节点数为m,则拓扑结构的层数n¢为公式(9),簇头节点总数nkey为公式(10):
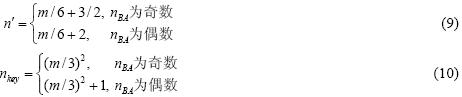
证明:因为BA每行有3个节点,所以每行基本监测区域BA的个数nBA=m/3,而监测区域的面积是所有BA面积的和,即s=(nBAx3l)2,将公式(1)代入s=(nBAx3l)2可得:

将公式(11)代入公式(8)得:
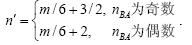
由每行的节点数m可知,总的节点数为m2.又因为每个BA中有1个簇头节点,且每行有3个节点,于是,整个监测区域内BA的个数nBA=(m/3)2,整个监测区域的关键节点数为(m/3)2(注:当nBA为偶数时,需要在监测区域正中间额外加一个协调器节点,总的簇头节点数为(m/3)2+1).因此,IA中簇头节点总数为
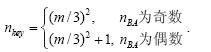
性质2. 设n¢为监测区域内拓扑结构的层次数,则监测区域内总的簇头节点数nkey为

证明:由性质1的公式(9)可得:

将公式(13)代入公式(11)可得:
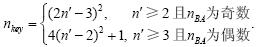
定义4(距离冗余度α). 设监测区域中两个节点间的理想距离为d1,实际的距离为d2(d2<d1),则α=1-d2<d1 (0<α<1)称为节点的距离冗余度.
性质3. 已知需要监测的面积为s,实际投入费用为f1,传感器的通信半径为D,每个叶节点的费用为C,则距离冗余度α为

证明:当组成监测区域的基本监测模块数n=1时,由图 2可得,相邻两个传感器节点的最大理想距离为d1=当n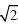 D/2>1时,相邻两个传感器节点的最大理想距离为d1=当n
D/2>1时,相邻两个传感器节点的最大理想距离为d1=当n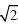 D/6
D/6
相邻两个传感器节点的实际距离为d1=当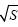
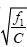 则距离冗余度为
则距离冗余度为
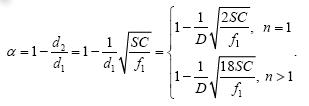
根据公式(14)可知:当d2>d1时,节点间不能进行正常通信,至少需要增加费用到f0;当d2=d1时,节点间能正常通信,但没有冗余,需要投资的费用最小,最小费用f0=( /l)2当d2<d1时,能进行正常通信,且有冗余,冗余度是α.
/l)2当d2<d1时,能进行正常通信,且有冗余,冗余度是α.
定理2. 设传感器的传输半径为D,实际监测的面积为sr,距离冗余度为α,则实际需要监测的拓扑结构的层数为

证明:在实际监测区域中,为了提高系统的可靠性,节点的实际距离是理想距离的(1-a)倍,因此,实际面积是理想面积的(1-a)2倍.因此,如果实际面积是sr,则理想面积是sr/(1-a)2.将此理想监测面积代入定理1的公式中,得到:
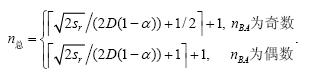
表 1的第2列~第7列分别计算了2层监测结构(基本监测结构)、3层结构、4层结构和N层结构的监测区域的行数、列数、节点数总数、簇头节点数(BA的个数)、理想监测面积和实际监测面积.
| Table 1 Comparison of different monitoring structure parameters 表 1 不同监测结构的参数比较 |
假设传输半径D为30m,实际监测面积sr取450m2~100 000m2(450为一个理想状态下基本监测区域BA的面积),距离冗余度a分别取0.1,0.3,0.6,0.9,得到正方形监测方案需要的拓扑层数与实际监测面积sr的关系如图 3(a)所示,监测方案所需要的簇头节点数与实际监测面积的关系如图 3(b)所示.
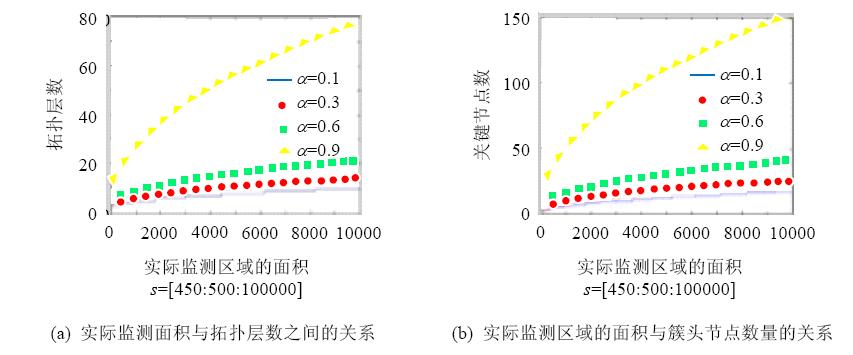 | Fig. 3 Simulation analysis to the relationship between actual monitoring area and the number of topological layer and area cluster head图 3 实际监测面积与拓扑层数和簇头节点的仿真分析 |
由图 3(a)、图 3(b)可以得出如下结论:距离冗余度对拓扑结构的层数和簇头节点数有较大的影响,冗余过小,对监测区域的可靠性不会起到很好的保障作用;然而冗余过大,却会造成部署成本急剧增长;当距离冗余度选择适当时,既可以有效地保障监测区域的可靠性,又不会使拓扑结构的层数和簇头节点数增长过快.
3 监测区域的可靠性保障机制与优化分析为了提高监测系统的拓扑可靠性,监测区域通常采用冗余策略,但过多的冗余会在费用和管理上带来困难,因此在实际部署时,根据实际需求对普通节点和关键节点采取不同的冗余策略:对监测区域的监测部分,采用距离冗余度α进行部分冗余策略来提高普通节点的可靠性;对监测区域的传输部分,采用动态倍增优化冗余策略来提高关键部分的整体可靠性.
3.1 监测区域中监测部分的可靠性保障机制与量化分析对于数量最大但能耗最少的普通叶节点,采用基于模冗余系统的部分冗余策略[12].根据实际需求,节点间的实际距离取理想距离的(1-α )(0<α<1)倍进行冗余,即在每行m个节点中都有am个节点冗余.
定理3. 设m行m列的正方形监测区域的距离冗余度为α,叶节点(或簇头节点监测部分)都是同构的,可靠
性均为R,则监测部分的可靠性为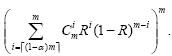
证明:首先计算每行的可靠性,根据要求,只要每行有效节点数mval大于等于该行节点总数m的(1-α)倍,就认为是可靠的,即mval≥(1-α)m.因为整行节点总数的1-α倍不一定能正好整除,因此取结果的上界,即é(1-α)mù.因为从每行m个任取é(1-α)mù个冗余的可靠性是é(1-α)mù个节点可靠,m-é(1-α)mù个节点不可靠,其可靠性为
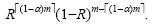
每行的可靠性是指在m个节点中至少有[(1-α)m]个节点有效,那么从第k行中的m个节点任取[(1-a)m]以上个节点的可靠性是:
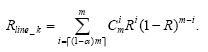
整个监测部分的可靠性是由m行组成,它们必须同时有效整个监测区域才算是可靠的,因此按m行串联的可靠性计算公式计算,即
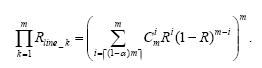
簇头节点的可靠性是整个监测系统可靠性的关键,为了提高系统的可靠性,对于诸如簇头节点(路由器)、Sink节点(协调器)等采用动态倍增优化冗余策略,使簇头节点的整体可靠性达到最好.
定理4. 设投资在簇头节点的总费用为b,理想监测区域面积为s,各簇头节点的各个冗余设备是同构的,并设其可靠性均为Rj,其价格均为ci,则监测区域传输部分的簇头节点的可靠性优化公式为
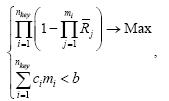
其中,nkey是簇头节点总数,Max代表可靠性最优.
证明:由定理1可知:根据监测区域面积s,可以计算出拓扑结构的层数n¢.根据性质2,从拓扑结构的层数n¢可以推导出簇头节点总数nkey.设第i个簇头节点共有mi个设备进行冗余可使整体簇头节点的可靠性最高,因为
各簇头节点是同构的,其可靠性均为Rj,不可靠性为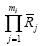 这些簇头节点所形成的并联结构不可靠,是指组成这个并联结构的每个设备都不可靠.每个簇头节点不可靠可用公式表示,这个并联结构的可靠性用1-
这些簇头节点所形成的并联结构不可靠,是指组成这个并联结构的每个设备都不可靠.每个簇头节点不可靠可用公式表示,这个并联结构的可靠性用1-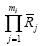
计算,则整体簇头节点的可靠性为

最优化设计是使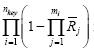 达到最大,因为对簇头节点总的投资不超过b,且各簇头节点的冗余设备价格是相同的,设其均为ci,则第i个簇头节点的总价格是cimi,监测区域中簇头节点总的价格为
达到最大,因为对簇头节点总的投资不超过b,且各簇头节点的冗余设备价格是相同的,设其均为ci,则第i个簇头节点的总价格是cimi,监测区域中簇头节点总的价格为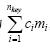 则约束条件为
则约束条件为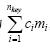 <b因此,整个优化计算由公式(17)获得:
<b因此,整个优化计算由公式(17)获得:

整个监测区域可靠是指信息监测和信息传输两个部分同时可靠,因此,这两个部分为串联结构.由定理3和公式(16)得到整个监测区域的可靠性公式为
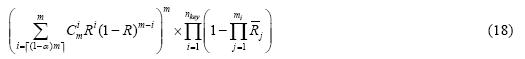
说明:公式(18)的已知条件是理想监测面积s,但是在实际情况下,已知的条件是监测的实际面积sr和传感器的传输半径D.由定理2可知,理想面积s与实际面积sr之间存在如下关系:s=sr/(1-a)2,又因为理想监测区域是正方形,其边长为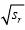 /(1 −α ).于是,由公式1可计算出理想监测区域的节点间距离l=
/(1 −α ).于是,由公式1可计算出理想监测区域的节点间距离l=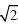 D/6用边长
D/6用边长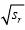 /(1 −α )除以节点间的距离l可计算出每行节点的个数m=3
/(1 −α )除以节点间的距离l可计算出每行节点的个数m=3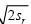 /(1 −α )D将m代入公式(18),即可得到实际监测
/(1 −α )D将m代入公式(18),即可得到实际监测
面积情况下的监测区域的可靠性.
4 基于双倍冗余与重传相结合的远程传输主干的可靠性保障机制与量化分析 4.1 基于双倍冗余的保障远程传输主干的传输架构在诸如三江源生态远程信息监控中,监测区域一般都处于偏远地区,互联网、有线专线等可靠的IT远程传输主干一般都没有,移动通信也比较弱,传输不是很稳定,有的地方甚至没有这些基础通信设施.从经济角度和实际传输环境出发,可以采用我国目前自主研发的北斗短信传输系统,但目前北斗的短信传输的可靠性也不是很理想,因此,提高远程传输主干的拓扑可靠性也是物联网远程监测中的一个重要问题.
目前,远程传输可以选择的通信形式包括GPRS、3G、互联网、卫星通信、微波、LDmesh、北斗卫星短信传输等.这些通信在传输内容的形式、费用、带宽上不尽相同,在实际部署时,根据监测区域的实际通信状况,在可靠性、费用等多种指标的约束下,选择两种不同传输方式同时传输以提高主干传输的可靠性.例如,使用电信营运商的3G信号和北斗短信传输系统进行双重并行传输,防止其中的某个传输信号不强或者不稳定带来的信息传输中断.图 4是远程监测的主干传输架构,其中,Rm1和Rm2表示双倍冗余传输主干,设其可靠性分别为rm1和rm2,则由并联结构的可靠性计算公式可知,其可靠性,Rs是监测区域网关,Rr是监控中心的接收网关,远程传输主干和远程反馈主干在实际中是相同链路.
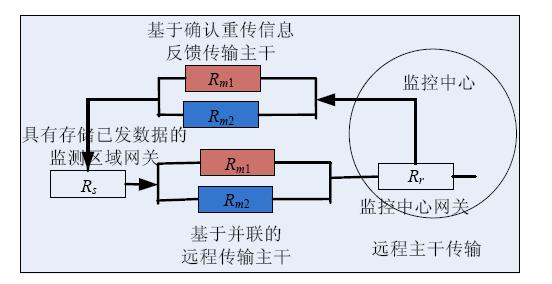 | Fig. 4 Trunk framework of remote monitoring with double redundancy and retransmission function图 4 具有双倍冗余和重传功能的远程监测的主干传输架构 |
重传是提高系统可靠性的一种重要措施,本文对远程主干传输采用确认重传机制来提高监测系统的可靠性,当监控中心网关Rr收到监测信息时就向监测区网关Rs发确认ACK,如果在规定的时间内没有收到信息,就向监测区域网关发重传RET信息.
定理5. 设远程重传系统由监测区域网关(其可靠性为rs)、信息发送和反馈主干(其可靠性均为rm)和监控中心网关(其可靠性为rr)组成,并设当传输失败时启动重传系统的概率为c,则整个重传系统第k次重传的可靠性由公式(19)计算获得:
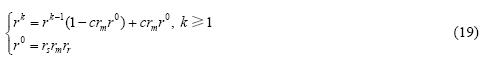
其中,rm=rm1rm2.
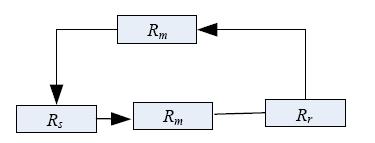
证明:因为在传输主干中用双并联冗余传输链路来提高传输主干的可靠性,其可靠性其中,rm1和rm2分别为图 4中Rm1和Rm2传输链路的可靠性.图 4等价简化为图 5,下面计算这个重传系统的可靠性.
 | Fig. 5 Equivalent simplification retransmission system from Fig. 4图 5 由图 4等价化简后的重传系统 |
正常传输(也称为第0次重传)是由监测区域网关Rs、传输主干Rm和监控中心网关Rr联合完成的,它们是串联结构,其可靠性r0=rsrmrr.
第1次重传的可靠性是当传输失败时,第1次重传需要通过Rm,Rs和Rr重新传输,其可靠性的计算是第1次正常传输的可靠性加上第1次传输失败(不可靠)的可靠性乘以第2次传输(第1次重传)的可靠性再乘以成功转换率c,具体公式如下:
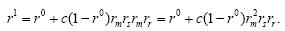
第2次重传的可靠性是第1次重传的可靠性加上第1次重传失败(不可靠)的可靠性乘以第2次重传的可靠性再乘以成功转换率c,具体公式如下:
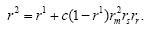
第k次重传的可靠性是第k-1次重传的可靠性加上第k-1次重传失败(不可靠)的可靠性乘以第k次重传的可靠性再乘以成功转换率c,具体计算见公式(20):

具体重传多少次,则与可靠性要求和重传系统中的每个设备本身的可靠性有关.假设要求的可靠性不低于
rmin,则至少重传的次数k可由rk≥rmin计算获得,即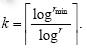
重传能够提高可靠性,但并非重传次数越多越好,因为当可靠性达到一定数量级后,再增加重传次数对可靠性的提高并没有多少帮助,反而增加了开销.因此,我们根据下式来确定最优重传次数i:
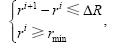
其中,DR表示精度.
上式的含义为若增加重传次数前后可靠性之差小于DR且当前可靠性满足最低要求rlimt时停止增加重传次数,此时的重传次数i即最优重传次数.对上述方案进行仿真,参数设置如下:重传次数最大为14、监测区域网关可靠性rs=0.95、信息发送和反馈主干可靠性rm=0.93、监控中心网关可靠性rr=0.95、传输失败时成功启动重传系统的概率c=0. 92、可靠性最低要求rmin=0.98、精度DR=0.005,则采取重传措施对远程传输主干可靠性的影响如图 6所示.
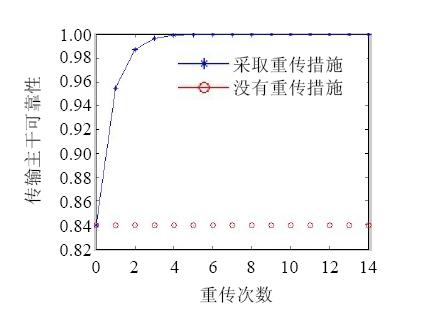 | Fig. 6 Simulation to the optimal times of retransmission图 6 重传次数优化仿真 |
实验仿真结果显示,重传可以有效地提高传输主干的可靠性.当重传次数低于4次时,效果最明显;当重传次数大于等于4次时,效果并不明显;当重传次数等于4时,既满足可靠性最低要求,又满足精度要求.因此在此仿真中,4为在以上仿真环境中的最优化重传次数.
整个监测系统包括3部分:① 由叶节点和簇头节点的监测部分组成的监测节点;② 由路由器和协调器组成的监测区域传输节点(关键节点);③ 由双重并行传输主干和网关组成的传输系统.如图 7所示,这3部分逻辑上是通过串联组成的整个系统,因此,整个监测系统的可靠性是各个部分的乘积.
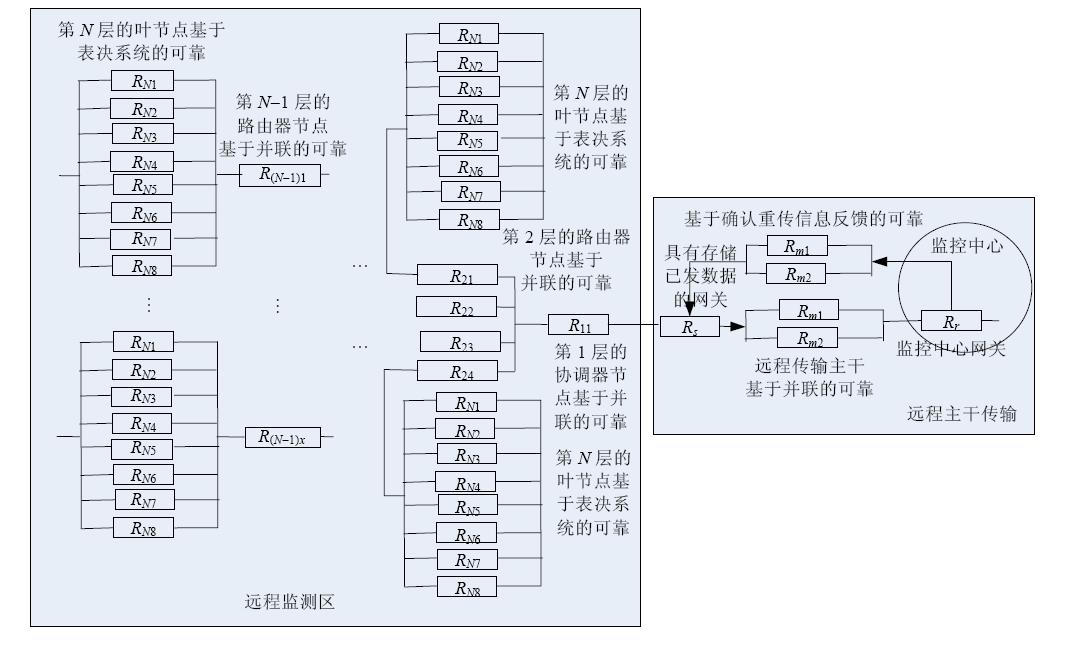 | Fig. 7 Transmission framework of the monitoring system 图 7 整个监测系统的传输架构 |
前面对偏远地区物联网远程监测系统的可靠性进行了理论计算和分析,下面通过实验进一步验证系统的相关特性和关系.因为距离冗余度a是由用户自己决定的,其大小的选择对监测系统的可靠性有很大的影响,因此,本文重点通过模拟验证整个监测系统的可靠性与距离冗余度a的关系.设信息监测节点的可靠性R=0.92、簇头节点转发数据的可靠性均为Rj=0.98、簇头节点采用双冗余备份mi=2、整个监测区域中节点的距离冗余度a取值为0到1、步长为0.05、监测区域网关的可靠性Rs=0.92、信息发送和反馈主干的可靠性Rm=0.85、监控中心网关的可靠性Rr=0.92、重传时成功转化率c=0.88,重传次数k=3(实际应用时,Rs,Rm,Rr,c应比此处高很多,在此为了便于效果的观察,取较小的数值),每行总的节点数m取6,9,30,60时的监测区域的可靠性与距离冗余度a的关系如图 8(a)所示,整个系统(监测区域+远程系统)的可靠性与距离冗余度a的关系如图 8(b)所示.
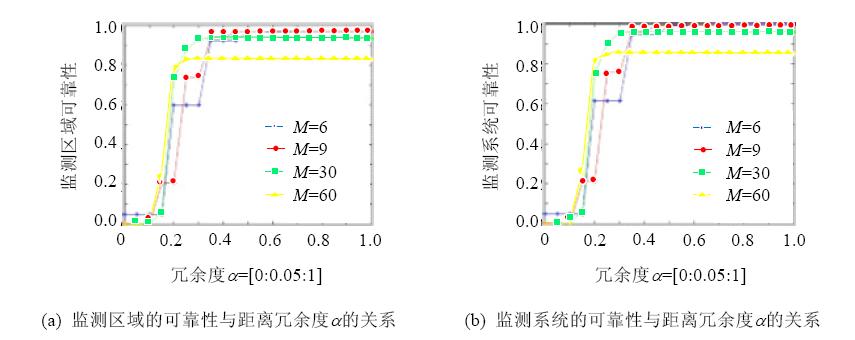 | Fig. 8 Relationship between distance redundancy and the reliability of monitoring area and monitoring system 图 8 监测区域和监测系统与距离冗余度的关系 |
(1) 从图 8(a)可以得出如下结论:随着m的增大,达到最优配置的a将减小;但同时,随着m的增大,当a接近1时,可靠性降低.这是因为随着m的增大,监测区域内的簇头节点将增多,簇头节点总的可靠性将下降,所以出现如图 8(a)所示的情况.因此,在选取a大小时,要进行折中考虑.
(2) 从图 8(a)和图 8(b)对比可以得出如下结论:当m取相同值时,由于采取了3次重传机制,在rs,rm,rr,c的取值较低时,整个系统的可靠性也不会降低很大.因此,重传对于提高主干传输的可靠性具有明显效果.
在传感器网络中,簇头节点既要感知信息,又要转发其他节点的信息,因此,簇头节点的负担较重,并且当无线传感器网络中的节点采取均匀部署的方式以后,簇头节点越靠近Sink节点,其负担越重.为防止靠近Sink节点的簇头节点过早死亡造成网络空洞,因此对簇头节点采取冗余,且处在不同级别的簇头节点冗余的个数不同.这样,原先的单个簇头节点变为一个簇头节点组.为了验证不同簇头节点组中失效的簇头节点个数对系统可靠性的影响,进行如下仿真实验:
假设共有10层簇头节点,第2层~第10层中的每个簇头位置均为一个簇头节点组.在每个簇头节点组中,簇头节点的个数遵循如下规律:第10层,即最下层簇头节点组中,每个节点组由2个簇头节点并联而成;第9层中的每个簇头节点组由3个节点并联而成;第8层中的每个簇头节点组由4个簇头节点并联而成;以此类推,直到第2层中每个簇头节点组由10个簇头节点并联而成.假设每个簇头节点的可靠性均为0.95.如图 9所示,得到第10层、第8层、第6层、第4层每个簇头节点组中簇头节点失效的个数与监测区域中簇头节点整体可靠性的关系(在此假设当某个簇头节点组中所有簇头均失效时,整体的可靠性为0).
从图 9可以看出:每个簇头节点组中只要还剩2个簇头节点,失效的节点对整体的可靠性就几乎没有影响;当某个簇头节点组中仅剩1个簇头节点时,整体可靠性会下降,但下降的幅度并不大;只有当某个簇头节点组中的簇头节点均失效时,整体的可靠性才降为0.因此,对簇头节点采取冗余可以有效地提高整体的可靠性.
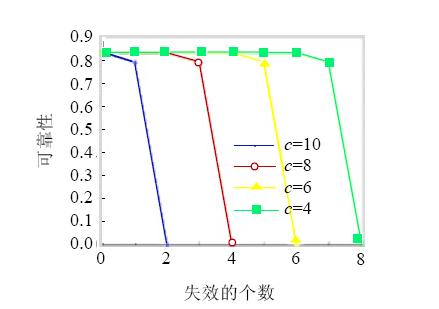 | Fig. 9 Relationship between the number of disabled cluster heads and reliability of monitoring system 图 9 失效的簇头节点个数与系统可靠性的关系 |
本文提出了偏远环境物联网远程实时监测中的一类均匀、可扩展的模块化层次拓扑结构模型,重点研究了正方形结构模型,包括监测模型所需的拓扑层次数与监测面积的关系,监测模型所需的簇头节点数与拓扑层次数、监测面积之间的关系.在保障监测系统可靠性方面,本文通过多种组合方案来进行可靠性的设计与优化.文章对基于物联网的大面积偏远地区远程实时监测的节点部署与可靠性保障具有重要的理论和实际借鉴价值.我们下一步将研究的内容是:针对大面积非正方形结构(如长方形、带拐角形状)的监测区域,通过正方形组合进行拓扑结构的拓展设计与优化,并进一步探究不同的节点位置和节点数量失效对系统可靠性的影响.
| [1] | Liu LP, Wang Z, Sun YX. Survey on coverage in wireless sensor networks deployment. Journal of Electronics & Information Technology, 2006,28(9):1752-1757 (in Chinese with English abstract). |
| [2] | Yoon Y, Kim YH. An efficient genetic algorithm for maximum coverage deployment in wireless sensor networks. IEEE Trans. on Cybernetics, 2013,43(5):1473-1483 . |
| [3] | Ahmad A, Balasubramaniam N. Optimal control-based strategy for sensor deployment. IEEE Trans. on Systems, Man, and Cybernetics, Part A: Systems and Humans, 2011,41(1):97-104 . |
| [4] | Monica M, Sharma AK. Comparative study of energy consumption for wireless sensor networks based on random and grid deployment strategies. Int’l Journal of Computer Applications, 2010,6(1):28-35 . |
| [5] | Li YJ, Pan J. Intelligent node deployment scheme for wireless sensor network. Computer Science, 2012,39(8):115-118,135 (in Chinese with English abstract). |
| [6] | Yao ZJ, Bai H, Yi WD. Reliability analysis on grid topology in wireless sensor network. Journal of Computer Research and Deployment, 2010,47(2):55-59 (in Chinese with English abstract). |
| [7] | Chakrabarty K, Iyengar SS, Qi H, Cho E.Grid coverage for surveillance and target location in distributed sensor networks. IEEE Trans. on Computers, 2002,51(2):1448-1453 . |
| [8] | Wint YP, Schmitt JB. Node deployment in large wireless sensor networks: Coverage, energy consumption, and worst-case delay. In: Kanchanasut K, ed. Proc. of the Asian Internet Engineering Conf. (AINTEC 2009). Urbana-Champaign: Association for Computing Machinery, 2009. 77-84. |
| [9] | Li HH, Fan J, Chen L. Application of grid method in deployment of wireless sensor network. Transducer and Microsystem Technologies, 2012,31(3):150-152 (in Chinese with English abstract). |
| [10] | Xu N, Cassandras CG. Optimal cluster-head deployment in wireless sensor networks with redundant link requirements. In: Azad AP, ed. Proc. of the 2nd Int’l Conf. on Performance Evaluation Methodologies and Tools. Urbana-Champaign: Association for Computing Machinery, 2007. 1-9. |
| [11] | Gautam AK, Patel R.Sensor deployment for geographic, load balanced hierarchical organization in wireless sensor networks. In: Patel RB, Singh BP, eds. Proc. of the Int’l Conf. on Method and Models in Science and Technology. Chandigarh: AIP Publishing, 2010. 99-105. |
| [12] | Shu T, Krunz M, Vrudhula S. Power balanced coverage-time optimization for clustered wireless sensor networks. In: Kumar PR, ed. Proc. of the 6th ACM Int’l Symp. on Mobile Ad Hoc Networking and Computing. Urbana-Champaign: Association for Computing Machinery, 2005. 111-120 . |
| [13] | Wu Y, Zhang L, Wu Y, Niu Z. Interest dissemination with directional antennas for wireless sensor networks with mobile sinks. In: Campbell A, ed. Proc. of the 4th Int’l Conf. on Embedded Networked Sensor Systems. New York: Association for Computing Machinery, 2006. 99-111. |
| [14] | Zhong JH, Zhang J. Ant colony optimization algorithm for lifetime maximization in wireless sensor network with mobile sink. In:Soule T, ed. Proc. of the 14th Int’l Conf. on Genetic and Evolutionary Computation. New York: Association for Computing Machinery, 2012. 1199-1204 . |
| [15] | Aitsaadi N, Achir N, Boussetta K, Pujolle G.Multi-Objective WSN deployment: Quality of monitoring, connectivity and lifetime. In: Roger P, eds. Proc. of the 2010 IEEE Int’l Conf. on Communications. Piscataway: Institute of Electrical and Electronics Engineers, 2010. 1-6 . |
| [16] | Ehrgott M, Gandibleux X. Approximative solution methods for multiobjective combinatorial optimization. TOP, 2004,12(1):1-63 . |
| [17] | Wen H, Lin C, Ren FY, Zhou J, Yue Y, Huang XM. Retransmission or redundancy: Transmission reliability study in wireless sensor networks. Science China Information Sciences, 2011,55(4):737-746 . |
| [1] | 刘丽萍,王智,孙优贤.无线传感器网络部署及其覆盖问题研究.电子与信息学报,2006,28(9):1752-1757. |
| [5] | 李燕君,潘建.无线传感器网络的节点智能部署方法研究.计算机科学,2012,39(8):115-118,135. |
| [6] | 姚振杰,白华,易卫东.无线传感器网络的格型拓扑可靠性分析.计算机研究与发展,2010,47(2):55-59. |
| [9] | 李海华,范娟,陈利.网格法在无线传感器网络部署中的应用.传感器与微系统,2012,31(3):150-152. |
 2014, Vol. 25
2014, Vol. 25


