2014, Vol.25 
随着半导体工艺的日臻成熟,处理器芯片上集成的晶体管越来越多,目前已突破10亿量级,图形处理器(graphics processing unit,简称GPU)的性能也因此得到飞速提升,并远远超过通用CPU[1].2012年,GPU集群已成为世界TOP 500超级计算机中主要的计算资源.GPU优良的计算性能,一方面得益于核心运算单元独享内存容量和内核数量的增长,另一方面,更依赖于并行计算平台中负载调度策略的程序实现.
CUDA和OpenCL是GPU系统中应用最广泛的并行计算平台.在这两类经典程序设计范式中,负载被定义为GPU上运行的一个或多个并行程序段(内核),并关联有程序运行时所需的数据资源.在GPU集群中,负载一旦被分配到某个GPU上,该负载就只能访问这个GPU独享的内存,而且,负载必须在其关联数据加载到独享内存后才能开始处理和执行.在过去的几十年间,主存和GPU独享内存之间数据传输带宽的提升速度一直落后于GPU内核数量的增长速度,数据传输延时问题变得不容忽视.特别是在实时系统中[2, 3],大规模并行负载同时加载到GPU上时,主存和独享内存间的数据传输时间成为影响系统全局性能的重要参数.目前,考虑数据传输的GPU内核负载调度还处于较低的自动化水平,这成为制约GPU系统全局性能提升的重要问题之一.
针对以上问题,本文综合考虑数据传输时间和负载均衡,对GPU上的大规模并行负载调度问题展开研究,将总负载makespan最小化作为GPU全局性能的优化目标,给出一系列能够同时提升负载执行并行度和缩短数据传输时延的调度策略.迄今为止,GPU负载调度的研究工作主要集中在处理器如何提升负载并行度上,其中代表性的工作有:Gregg等人[4]提出了一种GPU上细粒度的动态控制策略,实现对大规模负载的并行调度;Li等 人[5]提出了一类虚拟化方法,使多处理器上的不同负载共享GPU资源,提升负载执行的并行度;Kato等人[6, 7, 8]针对优先级、抢占和隔离等实时需求,提出了一系列实时计算系统上的GPU资源管理策略.以上研究尚未考虑GPU独享内存与主存之间的数据传输延时问题.对于GPU系统全局性能而言,尤其是在实时系统中,当大规模并行负载同时加载到存储器上时,数据传输和负载均衡同样重要.下面通过Nvidia Geforce GT 630M平台中的例子,说明数据传输在调度中的重要性.
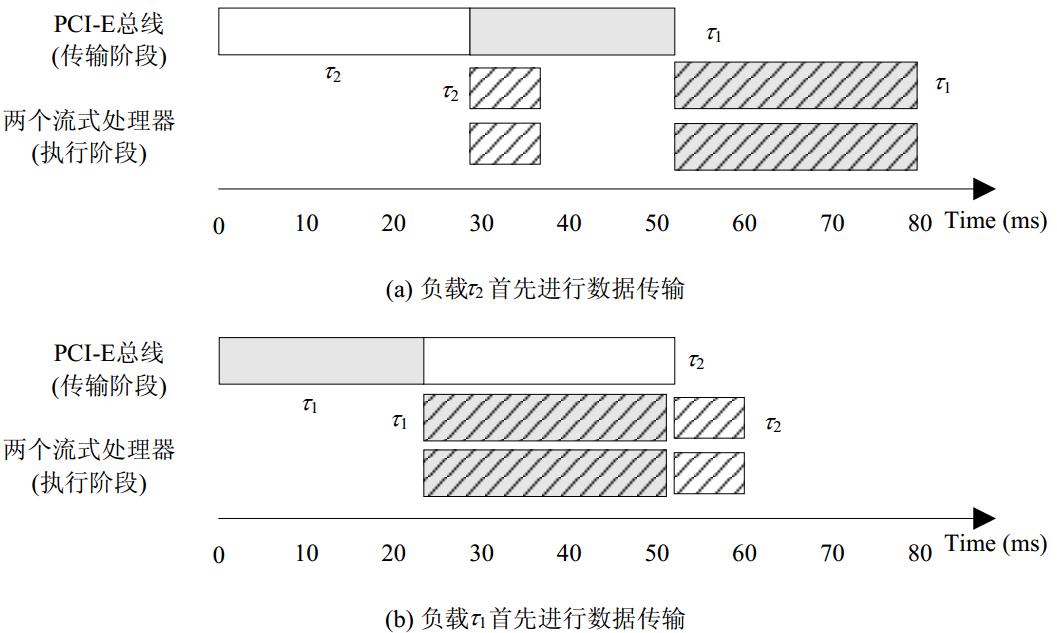
图 1给出了由Nvidia SDK开发的两段程序在GPU上调度的情况[9].其中,t1为异步API程序关联的负载,大小为32 768区块(每个区块的规模为1024KBx1KB);t2为向量加载程序关联的负载,大小为35 157区块(每个区块的规模为256KBx1KB);负载t1和t2均在GPU上由两个内核并行执行.通过API函数cudaEventRecord获取GPU流处理器时钟周期的方法对负载时间信息进行估算得到:t1(以及t2)的数据传输时间和负载执行时间分别为23.392ms和29.215ms(以及28.626ms和6.398ms).两负载数据传输顺序改变,将导致不同的调度结果:
首先,假设两并行负载任务t1和t2同时到达,若不考虑负载的传输时间,随机对负载进行调度,不妨设t2先于t1进行传输;然后,负载的第2阶段按照先来先服务(first-come-first-serve,简称FCFS)策略进行调度执行,如图 1(a)所示.这种调度方案对应的makespan值为81.233.
若综合考虑负载的传输时间和执行时间,先传输负载t1,如图 1(b)所示.在这种方案下,调度系统的makespan值降低至58.416.
本文的主要贡献如下:针对GPU上负载“传输-执行”联合调度问题,从理论上给出一系列多项式时间的近似结果.首先,将负载的时间信息和并行任务数与矩形域的二维空间联系起来,建立负载的2D双层矩形域模型;然后,将GPU上负载调度问题归结为一类新的Strip-Packing问题;最后,基于贪婪策略给出近似度为3的多项式时间近似算法,算法复杂度为O(nlogn).从文中近似算法能够很容易地得出GPU最优或近似最优的调度策略:在数据传输阶段采取负载排序调度,在负载执行阶段采取FCFS调度.这也从理论层面上证明了GPU系统采取“传输-执行”两阶段调度的正确性和有效性.
 | Fig. 1 Different results for scheduling two workloads t1 and t2by considering the transfer times or not[9]图 1 考虑传输时间与否对负载t1和t2调度结果的影响[9] |
本文第1节介绍GPU计算系统模型和问题定义.第2节提出调度问题的2D双层矩形Strip-Packing模型.第3节给出问题的近似算法以及相关的理论分析和证明.第4节是实验结果.第5节介绍多处理器调度领域在近似算法方面的相关研究进展.最后是结束语.
本文研究具有m个流式多处理器的单GPU计算系统,m为常数(m≥2).在GPU系统中,负载调度架构基于Linux 3.0.0.48内核设计,并遵循CUDA 5.0规范,如图 2所示.GPU上的负载调度分为两个阶段:(1) 负载关联的数据传输称为调度的第1阶段;(2) 负载在GPU上并行执行称为调度的第2阶段.
在本文的计算系统中,GPU独享内存和主存之间的数据传输采取异步模式,这具体由Linux内核中的wrapper模块应用二元信号量实现.也就是说,任何负载若要占用GPU的硬件资源(PCI-E总线),在主存和独享内存之间进行数据传输,必须先获取二元信号量,并实现对信号量的加锁操作.相应地,一旦某负载完成了数据传输操作,它必须释放二元信号量,实现对信号量的解锁操作.本文将数据传输占用PCI-E总线看作一种独立的计算资源,比如,在第1.3节的问题定义中,PCI-E总线被抽象为调度问题中第1阶段的单机资源.
注意到,在大规模并行负载同时进行数据传输时,如何控制二元信号量的锁操作、确定数据传输顺序,对计算系统全局性能有重要影响(详见图 1中实例).数据传输阶段的负载排序是本文关注的主要问题.
在负载执行阶段,Linux内核采用默认的FCFS等待队列实现并行负载的分配操作.即,先完成数据传输的负载先被加载到GPU上的多处理器上并行执行.多处理器对应第1.3节调度问题定义中的m台并行机器.
FCFS策略实现简单,不会占用额外的计算资源,但是调度效果会受到阶段1中数据传输顺序的影响.数据传输阶段不同的负载排序将导致不同的调度结果.FCFS调度策略是否能保证GPU系统的全局最优性,还尚未可知.本文研究GPU上“传输-执行”联合调度问题,第3节给出的近似算法结果从理论上证明:FCFS策略与数据传输阶段负载排序策略相结合的方法能够保证GPU系统全局最优或近似最优.
本文考虑GPU计算系统中的一组并行负载(又称任务)集合G={t1,…,tn},负载ti用三元组(trani,sizei,execi)表示,其中,trani是负载ti关联的数据从主存传输到GPU独享内存上所耗费的时间;sizei是负载ti运行所需的处理器个数,一般情况下,sizei需少于GPU中的处理器总数m;execi是负载ti在GPU上的执行时间.本文假设负载符合伙伴调度(gang scheduling)方式,即负载ti的所有并行程序块同时分配到一组处理器上执行,并且每个程序块的执行时间相同,且同时开始执行.
当系统加载ti时,以上三元组变量将被存储在Linux内核的task_struct结构中.下面介绍负载特征量在GPU计算系统中的抽象过程.
为了获取负载ti的数据传输时间trani,首先需要估算出由主存传输到GPU内存的数据量ai,以及PCI-E总线的有效带宽b;然后,数据传输时间trani即可由公式éai/βù计算得出.ti在经过数据传输后,即可加载到GPU上开始执行.
对于大多数程序而言,负载通常由大量的程序块构成,每个程序块又被划分为若干线程.GPU将每个程序块分配到一个流式处理器中执行,每个程序块中并行线程的数量由程序员根据处理器参数决定.
本文模型不具体考虑GPU上处理器内核运行时的动态参数,而是采取一种粗粒度的静态方法[8]估算出每个程序块中的并行线程数量.该方法基于如下考虑:GPU中一个处理器的计算资源是有限的,因此,一个负载加载到该处理器上的最大并行线程数量也是有限的.不妨设负载ti中的线程总数为mi,ti在一个处理器上能够并行运行的最大线程数为gi.在满足处理器资源约束的条件下,负载ti并行执行所需的机器数sizei等于émi/tiù.在第1.3节中,负载的并行程序块对应于任务在第2阶段的并行操作.
同一负载的所有并行程序块在GPU上的执行时间均相等,这是本文的重要假设之一.该假设在基于Nvidia SDK开发的绝大多数程序中普遍成立.
由上一节中负载并行程序块模型易知,在负载ti的sizei个并行程序块中,至少有sizei-1个程序块包含相同的线程数gi(剩余的一个程序块所包含的线程数一定小于gi,其线程数计算公式为mi mod gi).对于具有相同线程数的程序块,假设所有线程的执行时间均相同,则可应用文献[10]中的方法估算负载执行时间execi.另外,对于线程数小于gi的程序块,令其执行时间等于execi.这种近似使得调度算法的实际效果一定不会低于理论值.
GPU上“传输-执行”联合调度问题可归结为二阶段flow-shop调度问题,其形式化定义如下:
给定一般的任务集G={t1,…,tn}以及一个二阶段flow-shop调度环境,其中,阶段1只有1台机器,阶段2中有m台同构并行机.每个任务ti包含sizei+1个操作,其中,第1个操作oi只能在阶段1的单机上执行,其执行时长为trani.在oi完成之后,另外sizei个操作方可开工,且必须由第2阶段的sizei台机器同时并行执行(sizei≤m),这sizei个操作的执行时长均为execi.在每个时刻,1台机器只能执行1个操作,且1个操作只能由1台机器执行.另外,在操作执行过程中不允许抢占,即操作一旦开始执行,在它完成之前不能有中断发生.
问题的优化目标是:所有任务完成加工的时间makespan最短,其中,最优的makespan定义为Cmax.根据调度问题的三参数表示法[11],本文问题可记为F2(1,Pm)|sizei|Cmax.F2(1,Pm)表示二阶段flow-shop调度环境,其中,阶段1和阶段2的机器数分别为1和m.sizei代表并行任务集合,即任意任务t i包含sizei个操作,其必须在第2阶段的机器上同时并行执行.
问题F2(1,Pm)|sizei|Cmax属于强NP困难问题,甚至在最简单的F2(1,2)情况下该结论也成立,见推论1.为了解决该强NP困难问题,本文首先给出原问题的二维双层矩形Strip-Packing模型(见第2节),然后基于Strip- Packing模型给出F2(1,Pm)|sizei|Cmax的近似算法和理论结果.
推论1. 问题F2(1,Pm)|sizei|Cmax是强NP困难问题,甚至当sizei=1且m=2时,该结论也成立.
证明:令每个任务在第2阶段仅包含1个子操作,F2(1,Pm)|sizei|Cmax即等价为文献[12]中的F2(P)|×|Cmax问题,由文献[13]即可证明阶段1的机器数为1、阶段2的机器数为2的F2(P)|×|Cmax为强NP困难问题.& nbsp;
由第1.3节的定义可知,本文的问题属于并行任务调度(multiprocessor task secheduling,简称MTS)问题在两阶段流水调度环境中的扩展.传统的单阶段MTS问题已有大量的算法理论研究[14, 15, 16, 17, 18, 19, 20, 21, 22, 23],其中大多数算法结果主要基于一种二维Strip-Packing模型[23].Strip-Packing模型应用矩形域的二维空间刻画任务的执行时间和并行子操作数这两类特征参数,是MTS问题天然的理论模型之一.然而,现有的Strip-Packing模型尚未扩展到二阶段调度领域,不能用于两阶段MST问题的近似算法研究.为此,本节首先在第2.1节建立两阶段并行任务的双层矩形域模型,其中,矩形的两层子域具有不同的属性,并且满足不同的约束.这些属性和约束用来刻画并行任务两阶段子操作的时序关系和执行时需要满足的计算资源约束.第2.2节给出了双层矩形域的属性和约束的形式化定义,并最终将F2(1,Pm)|sizei|Cmax归结为2D双层矩形Strip-Packing问题求解.
的对应关系
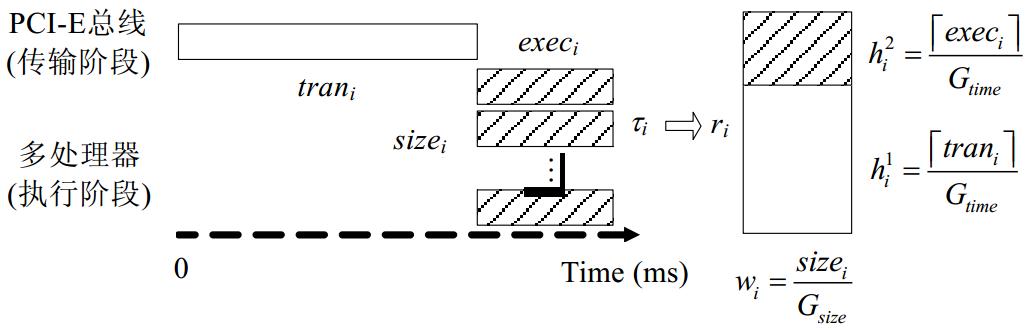
任务ti对应的矩形域ri如图 3所示.
 | Fig. 3 Rectangle model for workload ti图 3 任务ti对应的矩形模型 |
ti两阶段的子操作分别对应矩形ri的双层区域,其中,第1阶段的子操作oi对应底层的空白矩形域,执行时间trani对应空白域的高度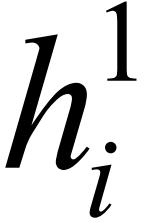
第2阶段的sizei个子操作对应上层的条纹矩形域,执行时间execi对应条纹域的高度
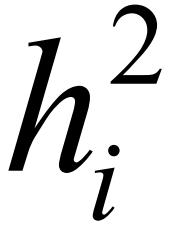.另外,任务在第2阶段执行所需的并行机器数sizei对应矩形ri的宽度wi.由第1.3节的定义可知,sizei 小于等于第2阶段总机器数m,因此,并行机数m也对应一个宽度值W,使得"ti∈G,ti对应矩形ri的宽度wi≤W.为了方便问题求解,令W=1,对sizei进行归一化,得到落在[0,1]区间的矩形宽度值wi.相应地,通过为负载任务的执行时间选择合适的阈值Gtime,对矩形域的高度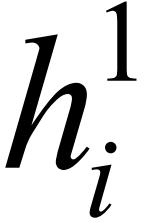和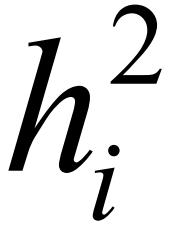做与矩形宽度类似的规范化处理.具体的规范化过程见
算法1.
算法1. 负载任务特征参数的规范化算法.
输入:任务集合Γ及并行机器数m.
输出:规范化的双层矩形域集合.
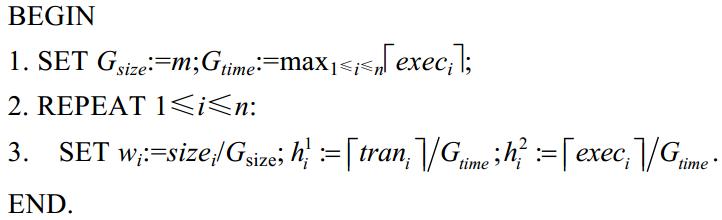
由算法1易知:经过规范化后,任务负载对应的矩形上层条纹域落在[0,1]x[0,1]区域内,底层空白域落在[0,1]x[0,hg]区域内,hg为max1≤i≤n{trani}/Gtime,可能大于1.这种规范化矩形域更有利于构造近似算法.而且,算法1中第1步和第3步的取整操作能够保证第 3节中算法的实际效果优于理论值.
在经过负载任务参数规范化后,问题F2(1,Pm)|sizei|Cmax可转化为2D双层矩形Strip-Packing问题,其形式化的定义为:给定2D双层矩形域列表L=(r1,…,rn),其中,每个矩形ri均关联三元组且满足0≤wi,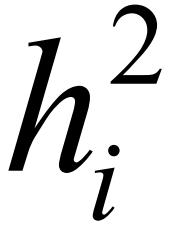≤1Ù 0≤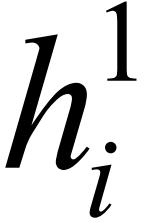≤hg,如图 3所示.定义列表L的面积(高度)为L中所有矩形的面积(高度)之和.列表L上Strip-Packing问题的目标是:在一个有限二维区域[0,1]x[0,+∞]中,为L中每个矩形域ri的空白域和条纹域分别指定一个位置坐标<xi,yi>和<xi,y'i>(也可简记为三元组<xi(yi,y'i)>使得:
(1) 每个矩形ri的条纹域均在其空白域之上,且彼此不相交,即,∀ri∈L,有
(2) 所有矩形的上层条纹域彼此不相交,即,∀ri,rj∈L,有:
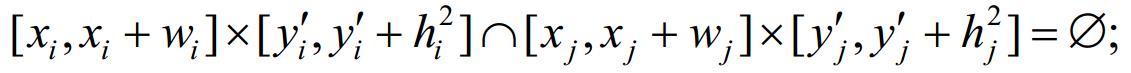
(3) 区域[0,1]x[0,+∞]中任一水平线最多与1个矩形空白域相交,即,∀ri,rj∈L,有:
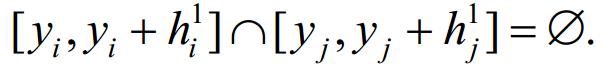
在区域[0,1]x[0,+∞]中,若矩形ri的空白域和条纹域分别定位在[xi,xi+wi]x[yi,yi+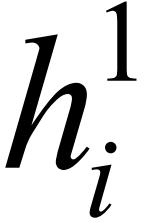]和[xi,xi+wi]x[y'i,y'i+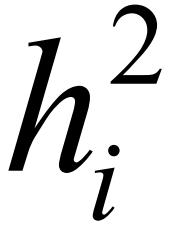]两区域,则yi为空白域下确界,yi+yi+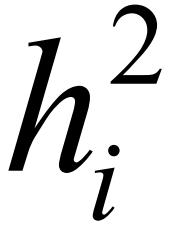为空白域上确界(同时也是条纹域的下界),y'i是条纹域的下确界,y'i+h2i是条纹域的上确界,同时也是整个矩形域ri的上确界.列表L的Strip-Packing高度即为L中所有矩形上确界的最大值.问题最优解(L的Strip-Packing高度最小值)定义为Opt(L)=inf{f的高度|f是L的任意Strip-Packing解}.
例1:图 1中两负载任务t1和t2对应的矩形域分别为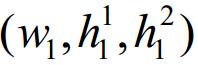ri
和ri
,如图 4所示.
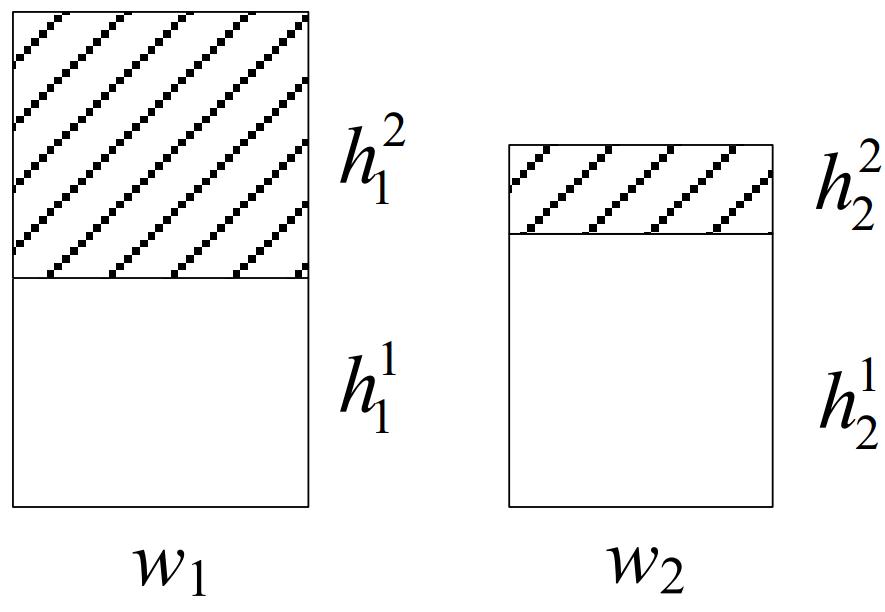 | Fig. 4Rectangle models for t1 and t2 图 4 t1和t2对应的矩形模型 |
由算法1可得,w1=w2=1,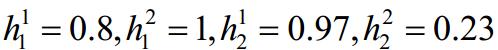
.矩形列表L=(r1,r2)在二维区域[0,1]x[0,+∞]中两组可行的Strip-Packing解如图 5(a)和图 5(b)所示,分别对应图 1(a)和图 1(b)中的两组负载分配方案.其中,第1组解的高度为2.77,第2组解的高度为2.03.显然,第2组解更优,对应在F2(1,Pm)|sizei|Cmax问题中的解为:在第1阶段,子操作o1在o2之后执行;在第2阶段,t1和t2按照FCFS策略进行调度即可.
 | Fig. 5Two strip-packing solutions with different heights for Instace 1图 5 例1中两组不同高度的Strip-Packing解 |
例1直观地给出了Strip-Packing问题和调度问题之间的对应关系.在2D双层矩形Strip-Packing问题中,条件(1)利用同一矩形双层域之间的互斥性,刻画任务两阶段子操作顺序执行的特性;条件(2)利用不同矩形条纹域之间的互斥性,刻画在每一时刻,1台机器只能执行1个操作,以及1个操作只能由1台机器执行的约束条件;条件(3)利用不同矩形空白域之间的互斥性,刻画调度问题第1阶段仅有1台机器的约束条件.另外,调度问题中的不可抢占条件由矩形空白域和条纹域的完整性刻画.Strip-Packing问题的最优解Opt(L)对应于F2(1,Pm)|sizei| Cmax问题的最早完工时间Cmax.综合本节和第1.3节的问题定义易知,Strip-Packing问题中的最优解即为调度问题参数规范化后的最优解.本文将在第3节给出Strip-Packing解转化为F2(1,Pm)|sizei|Cmax解的算法.
本节讨论一种满足条纹域可塑假设的Strip-Packing解,又称为可塑解.相应地,本节的假设条件又称为可塑条件,具体指以下3个方面:
(1)每个矩形ri的条纹域可在总面积wix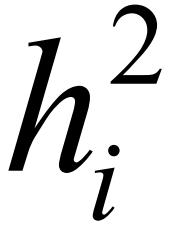保持不变的前提下,改变宽度和高度.设ri条纹域的宽度和高度增量分别为Dw和Δh,则有0<wi+Δw≤1,0<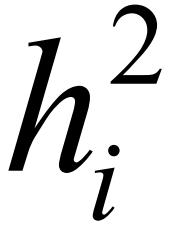+Δh,ΔwxΔh<0成立,并且
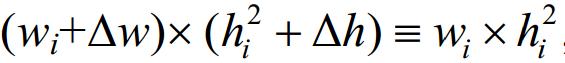如图 6(a)所示.
(2) 每个矩形ri的条纹域[0,wi]x[0,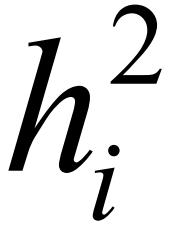]可被水平线切割分为多个子条纹域([0,wi]x[0,hi1],[0,wi]x[0,hi2],…, [0,wi]x[0,hik]),且
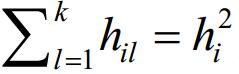如图 6(b)所示.另外,这k个子域也可在不改变面积的前提下改变宽度和高度.即,矩形域对条件(1)和条件(2)可以递归性地相互嵌套.
(3) 每个矩形ri的条纹域与空白域允许相交,但条纹域下界y'i不能低于相应空白域的下界yi,如图 6(c)所示.该条件是第2.2节Strip-Packing问题中约束条件(1)的松弛.
前两个假设条件分别对应flow-shop调度领域中的两个经典假设,其中,条件(1)对应任务可变性(malleable),即,任务可以在执行过程中任意改变并行度[2];条件(2)对应可抢占性[24],即,任务在执行过程中允许中断.易知,满足任务可变性和可抢占条件的调度解通常优于任务不可变且不可抢占的解.
另外,假设条件(3)在F2(1,Pm)|sizei|Cmax中即对应允许负载执行操作和数据传输操作同时并行执行.提出该假设是为了方便计算问题解的下界.
综上所述,满足以上3个假设条件的可塑解是Strip-Packing问题的下界.接下来,第3.2节将Strip-Packing问题的任一可行解转化为可塑解,同时获得问题的下界.
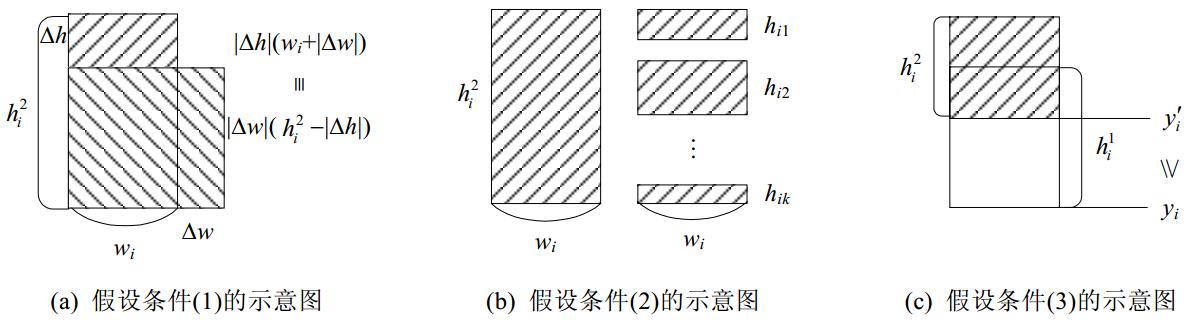 | Fig. 6Moldable assumptions图 6 可塑性假设 |
给定Strip-Packing问题任一可行解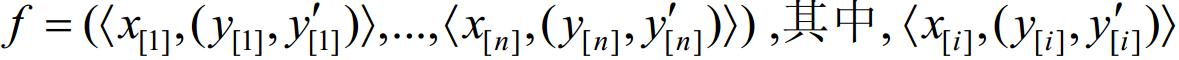
为第[i]个矩形在二维区域[0,1]x[0,+∞]中的坐标,不妨设f中矩形按空白域下界递增序排列,即y[1]<y[2]<…<y[n].算法2给出了由可行解f转化为Strip-Packing可塑解fm的步骤.
算法2. Strip-Packing可行解到可塑解的转化算法.
输入:Strip-Packing可行解f.
输出:Strip-Packing可塑解fm.
注意到,第3.1节的假设条件(3)允许矩形条纹域与空白域相互重合,因此,算法2的目标是尽量让每个矩形的条纹域回填到其相应的空白域中,以提高二维区域中条纹域的密度.算法从水平位置最低的矩形空白域开始扫描,首先获取空白域所在的二维域中不含条纹域的空白区(算法第2行),然后将相应条纹域(或部分)填入到该空白区内(算法第3行~第8行).根据第3.1节的假设条件(1)和条件(2),条纹域可任意调整宽度和高度,并可以任意横向切割,因此在理论上,条纹块回填到空白区的面积为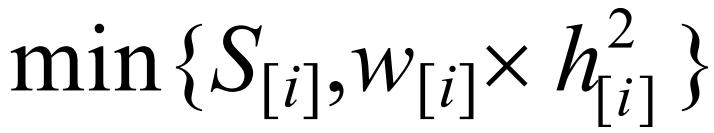
.由算法2不难得出定理1.
定理1. 满足可塑假设(1)~(3)的最优解值是Strip-Packing问题下界.
证明:对于Strip-Packing问题任意的可行解f,都可应用算法2将其转化为满足假设条件(1)~(3)的可塑解fm.可行解f中任一矩形r[i]的条纹域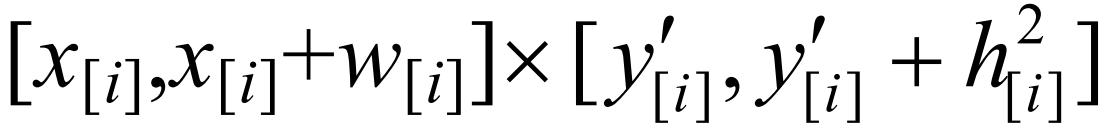
均可全部或部分回填到其关联的空白区S[i]中,如图 7所示.如果存在1≤i≤n,使得S[i]>0,则回填过程分为两种情况:(1) 若条纹域面积小于等于S[i],则整个条纹域可回填到S[i]中(如算法2第4行、第5行);(2) 否则,条纹域的上半部分回填到S[i]中(如算法2第7行、第8行).以上两种情况均降低了矩形r[i]条纹域的上确界,f中的其他矩形r[j](i<j≤n)即可进行相应的位置调整,填补r[i]条纹域减少的部分.最终,算法2求得的fm,其高度必定小于f的高度.另外,若所有S[i]均等于0,则经过算法2求得的fm与原f相同,fm的高度亦与f相同.综上所述,任意Strip-Packing可行解f的高度均大于等于其相应可塑解fm的高度.因此,最优可塑解值是Strip-Packing问题的下界.
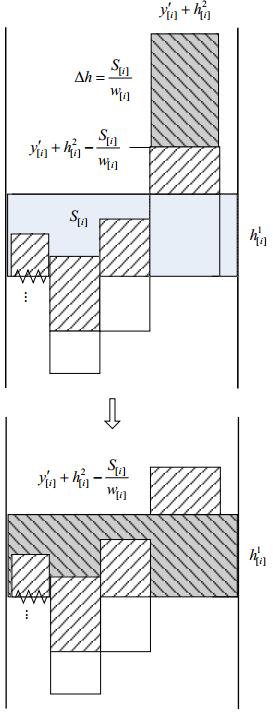 | Fig. 7Heights of the striped regions decrease after backfilling图 7 条纹域回填后高度变小 |
在矩形列表L的Strip-Packing问题中,设满足可塑假设的最优解为f*m其高度定义为Opt(Lm).由定理1易知,Opt(Lm)≤Opt(L).接下来,在第3.3节将f*m扩张为原Strip-Packing问题的可行解,并给出Strip-Packing问题的上界.
本节的目的是获得Strip-packing问题最优解的上界Optu(L),如定理2所述.
定理2. 矩形列表L上Strip-packing问题的上界Optu(L)=Opt(Lm)+2
证明:为了证明定理2,Strip-Packing最优可塑解f*m按算法3给出的步骤扩张为可行解fu.
算法3. Strip-Packing可塑解到可行解的转化算法.
输入:Strip-Packing可塑解f*m
输出:Strip-Packing可行解fu.
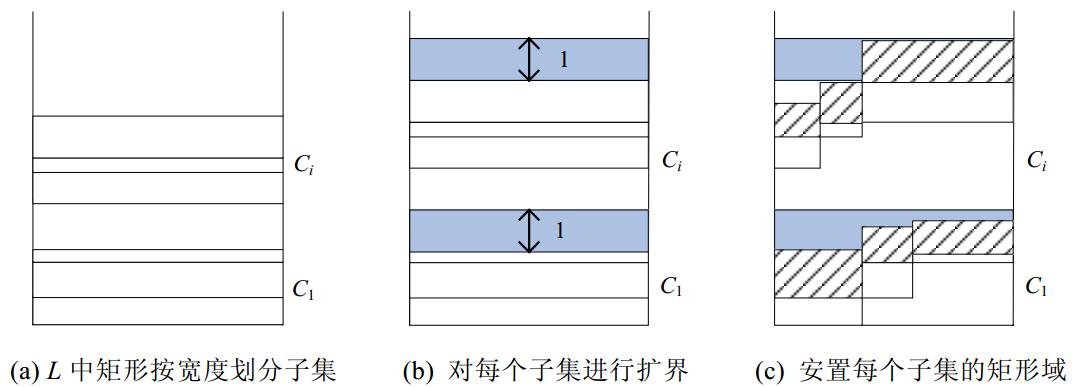
该算法分为3个阶段:(1) 按照可塑解f*m中矩形空白域下界的递增序,将矩形集合L划分为若干互不相交的子集{C1,…,Ck},如图 8(a)所示(算法的第3行、第4行);(2) 将每个子集Cj对应的空白域扩界,即,在Cj最顶端空白域的上界基础上再增加1个单位空白区[0,1]x[0,1],如图 8(b)所示(算法的第6行、第7行);(3) 将Cj安置到扩张后的空白域内,如图 8(c)所示(算法的第8行、第9行).
在阶段(1)中,算法的第3行保证了每个子集Cj中矩形的宽度之和小于等于1.这意味着Cj中的矩形一定能顺次排布在[0,1]区间内,不会超过有限二维区域的横向边界.由于L中每个矩形ri条纹域的高度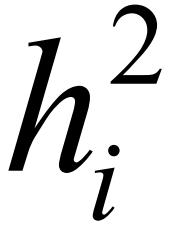≤1,阶段(2)恰好为每个Cj扩界1个单位,所以Cj中每个矩形的条纹域均可安置在其空白域之上,且高度不超过hlow+1,如图 8所示.
 | Fig. 8 Transform from strip-packing moldable solution to the feasible one 图 8 Strip-Packing可塑解转换为可行解 |
注意到,相邻的两个子集Cj和Cj+1的宽度之和一定大于1,否则,依据算法3的第3行、第4行,Cj和Cj+1应合并为一个矩形子集.因此,算法3中的扩界次数不超过2即算法求得的Strip-Packing问题可行解的上界Optu(L)为Opt(Lm)+2从而定理2得证.&nbs
p;
近似算法分为两个阶段:首先,基于贪婪策略求出Strip-Packing问题最优的可塑解f*m然后,再应用算法3对f*m进行扩界,得到可行解fu.两个阶段的全局算法描述如下:
算法4. Strip-Packing问题的近似算法.
输入:矩形列表L.
输出:Strip-Packing可行解fu.
定理3. 算法4能够求得Strip-Packing问题的最优可塑解.
证明:首先给出算法4求得可塑解的取值.根据算法4的第2行、第3行,将L中所有矩形对应的空白区S1,…,Sn放置在有限域[0,1]x[0,+∞]中.所有空白区的高度之和为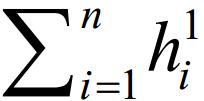
算法4的第4行~第11行是将矩形条纹域回填的过程,面临两种情况:
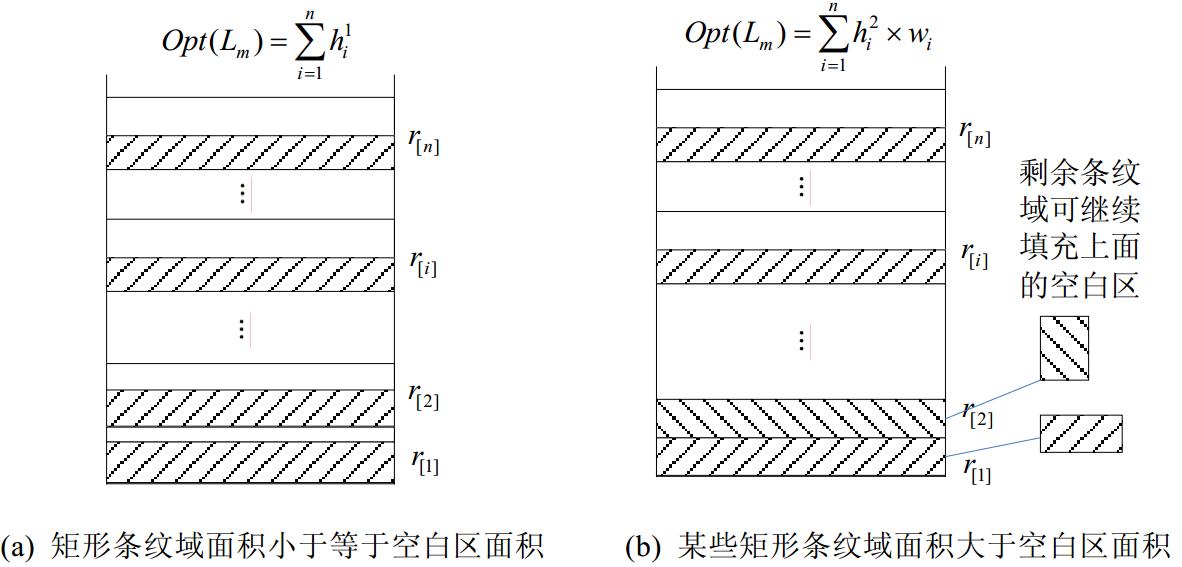
(1) 每个矩形r[i]的条形域面积均小于等于其对应的空白区面积Si(算法的第4行),在这种情况下,所有条纹域均回填到各自的空白区内,回填操作不影响可塑解的高度,如图 9(a)所示.
 | Fig. 9 Backfilling with striped blocks图 9条纹域的回填 |
(2) 存在部分矩形的条纹域面积大于其对应的空白区面积(算法的第7行).根据算法的第1行易知,这类矩形的空白域均安置在有限域[0,1]x[0,+∞]的底层部分,如图 9(a)所示.不妨设这部分矩形为(r[1],…, r[k]),其关联的剩余条纹域(见算法的第10行)为(R[1],…,R[k]).根据算法的第11行以及第3.1节的假设条件(1)和条件(2),可将每个R[i]任意调整形状和水平切割,将其填入空白区Sk+1,…,Sn的剩余面积中. 若剩余条纹域未填满所有空白区,则此二次回填操作并未改变可塑解高度,其值依然为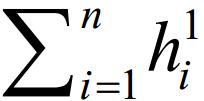若剩余条纹域填满所有空白区,则继续填入[0,1]x[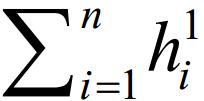,+∞]区域,则该操作改变可塑解的高度,其值为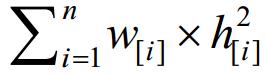
易知:针对情况(1),可塑解的最低高度即为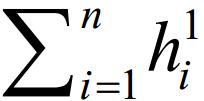对于情况(2),可塑解的最低高度为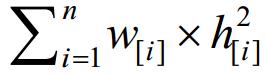因此,算法4求得的可塑解值为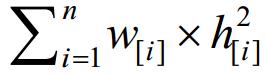
接下来给出问题最优可塑解的下确界.
注意到,在有限域[0,1]x[0,+∞]中,一条水平线不能与两个矩形的空白域同时相交,因此,所有空白区的高度之和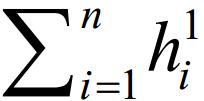为问题可塑解的下界.又因为在理想情况下,所有矩形条纹块经过可塑性条件(1)和条件(2)递归式调整,无空隙地放置在有限域[0,1]x[0,+∞]内.此时,可塑解的另一下界为
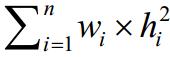故可塑解的下界解大于等于
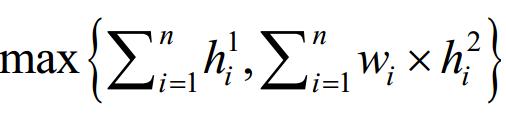已证明算法4求得的可塑解值等于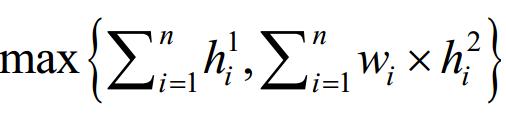综上所述,算法4能够求得Strip-Packing问题的最优可塑解.
定理5的充分条件是:数据传输时间大于单个处理器上的负载执行时间.本文研究的即是大规模并行负载同时加载到GPU上的问题,数据传输时间往往是不可忽视的问题参数.定理5刻画了数据传输时间大于负载执行时间的情况,在这种情况下,算法4具有常近似度.若存在负载执行时间大于数据传输时间的负载实例,算法4求得的解则具有伪多项式上界,如定理4所述.
注意到,算法4通过调用算法3将每个矩形的条纹域直接放置在其空白域上,这对应负载在数据传输完成后立即执行的情况,符合GPU内部的FCFS调度策略.基于此,可给出在F2(1,Pm)|sizei|Cmax问题的两阶段调度策略,如算法5所示:首先,在第1阶段,根据算法4对负载排序,按照顺序进行数据传输(算法5的第1行~第3行);然后,在第2阶段,应用FCFS策略调度负载在GPU多处理器上执行(算法5的第4行、第5行).
算法5. F2(1,Pm)|sizei|Cmax问题的两阶段调度算法.
输入:负载任务集合G及并行处理器个数m.
输出:负载的数据传输及执行次序.
为了验证本文算法的有效性,本节针对由4类负载组成的测试集进行实验.这4类负载的名称分别为vectorAdd,incrementKernel,BlackScholesGPU和pad-DataClampToBorder.对于每类负载,又考虑两组不同的参数,见表 1.因此,共生成了16组负载集合用于测试.每组负载集合详细的参数预估算法详见文献[9].
图 10给出了本文算法、随机排序算法以及基于穷举解法(最优解)之间的比对结果
16组实验数据表明:本文算法明显优于随机排序算法,并十分接近最优解,Gap值平均为1.34%.另外,本文算法有6组结果等同于最优解.
 | Fig. 10 Makespans obtained by our algorithm, ramdom and emuneration strategies图 10 本文算法、随机算法及枚举策略的求解结果 |
本节介绍相关问题的近似算法结果.注意到,本文研究的GPU上“传输-执行”二阶段调度问题在运筹学领域属于多阶段多处理器流水车间调度(国际上通常称为flexible flow shop或hybrid flow shop,简称HFS)和并行任务调度交叉的范畴.在过去的几十年间,多阶段和并行任务这两类特性很少放在一个问题中研究,HFS和MTS这两个问题分别在各自的研究范畴取得了众多经典的近似算法理论结果.
HFS问题的近似结果始于20世纪70年代,Sahni[25]为机器数固定的HFS问题给出了具有伪多项式上界的完全多项式近似策略(fully polynomial time approximation strategy,简称FPTAS).Hochbaum和Shmoys[26]研究了机器数作为变量的问题实例,并为该问题提出了目前最好的PTAS算法.Hall[27]研究了阶段数和机器数均为常量的问题,提出了一种优美的PTAS算法,能够给出问题的多项式上界,改进了Sahni[25]的结果.Williamson[28]研究了阶段数为变量的问题,证明了该问题不存在近似度小于5/4的PTAS算法.Jansen和Sviridenko[29]研究了机器数为变量的HFS问题,应用动态规划技术给出了近似度为3/2的PTAS算法.对于二阶段的HFS问题,众多学者给了很多近似算法[30, 31].这些算法的近似度都大于等于3/2.Schuurman和Woeginger[32]基于线性规划技术证明了二阶段HFS问题具有近似度为(1+e)的PTAS算法,这是HFS近似算法研究中里程碑式的成果.近年来,具有特殊约束条件的HFS问题特例得到研究.Xie等人[24]为了满足可获性(availability)约束的二阶段HFS,给出了近似度为3的近似算法.Sevastyanov[33]研究了多阶段共用一个机器集合的情况,并进一步改进了Hall[27]的近似结果. Choi等人[34]研究了第1阶段单机、第2阶段有m台机器,且每个阶段任务的执行时间均相同的情况,并给出了PTAS算法.该算法在m=2时,具有常数近似度为5/4;在m≥2时,近似度变为 ((1+m2)1/2+m+1)/2m.HFS最新的研究结果见文献[35, 36, 37].
MTS问题的近似算法研究,最初受到资源约束调度问题近似结果的启发.1975年,Garey等人[14]为资源约束调度问题给出了近似度为2的多项式时间算法.Ludwig等人[15]发现,MTS中的处理器可看做一种调度资源.于是,借鉴Garey和Granham的思路,证明了MTS问题多项式时间近似算法的存在性.Jansen等人[16]以及Amoura等人[17]分别对机器数固定的问题实例进行了研究,提出了若干PTAS算法.对于机器数为变量 的问题,Scharbrodt等人[18]提出了近似度为3和(2+e)的PTAS算法,并证明了对于固定机器数的问题不存在近似度低于3/2的PTAS算法.Diedrich等人[19]针对机器数固定和不固定两种情况,提出了近似度为(3/2+e)的PTAS算法,但是该算法应用了大量的枚举策略.Jansen等人[20]改进了文献[19]的工作,将近似度降低到3/2,并且避免了复杂的枚举操作.另外 ,Jansen研究团队还研究了异构机器MTS问题的近似算法[21],并给出了可变性并行任务的(3/2+e)近似度算法[22].关于MTS问题最新的研究见文献[23].
二阶段并行任务调度问题的研究一直集中在智能算法和启发式算法[38].目前,该问题仅有1项关于近似算法的研究.2011年,UIUC大学的Moseley和Yahoo研究院的Dasgupta等人[39]将Map-Reduce问题归结为一类二阶段并行任务调度问题,并给出了近似度为12的算法.而本文将GPU上负载调度问题归结为第1阶段单机、第2阶段有m台机器的二阶段并行任务调度问题,并给出了近似度为3的多项式时间算法.
本文给出了GPU上大规模并行负载调度问题的近似算法.文中综合考虑数据传输和负载执行时间,将GPU上负载调度问题归结为一类二阶段并行任务调度问题F2(1,Pm)|sizei|Cmax.然后,将负载任务的时间信息和并行机器数与矩形域的二维空间联系起来,为此类问题建立了2D双层矩形Strip-Packing模型,进而将F2(1,Pm)|sizei| Cmax中makespan最小化问题转化为列表L中矩形在有限域的最佳安置问题.基于可塑性假设,本文提出了一种多项式时间的近似算法,计算复杂度仅有O(nlogn).该算法采用二阶段策略,即,先在数据传输阶段进行负载排序,再在GPU内核中基于FCFS策略调度,因此易于在操作系统中实现.另外,算法相关的理论分析和实验结果也证明了这种两阶段调度策略能够保障GPU性能全局最优或近似最优.
致谢 感谢在NASAC 2013会议上,南京大学李宣东教授、东北大学于戈教授等出席了本文的报告,并提出了宝贵意见.感谢匿名审稿专家提出的建设性修改建议.
| [1] | Lin YS, Yang XJ, Tang T, Wang GB, Xu XH. A GPU low-power optimization based on parallelism analysis model. Chinese Journal of Computers, 2011,34(4):706-716 (in Chinese with English abstract) . |
| [2] | Lin YH, Kong FX, Xu HT, Jin X, Deng QX. Minimizing engergy consumption for linear speedup parallel real-time tasks. Chinese Journal of Computers, 2013,26(2):384-392 (in Chinese with English abstract) . |
| [3] | Tan GZ, Sun JH, Wang BC, Yao WH. Solving Chinese postman problem on time varying network with timed automata. Ruan Jian Xue Bao/Journal of Software, 2011,22(6):1267-1280 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4033.htm |
| [4] | Gregg C, Dorn J, Hazelwood K, Skadron K. Finegrained resource sharing for concurrent GPGPU kernels. In: Proc. of the 4th USENIX Conf. on Hot Topics in Parallelism. USENIX Association Berkeley, 2012. 10-16. |
| [5] | Li T, Narayana VK, Araby EE, Ghazawi TE. Gpu resource sharing and virtualization on high performance computing systems. In: Proc. of the 2011 Int’l Conf. on IEEE Parallel Processing (ICPP). IEEE, 2011. 733-742 . |
| [6] | Kato S, Lakshmanan K, Kumar A, Kelkar M, Ishikawa Y, Rajkumar R. RGEM: A responsive GPGPU execution model for runtime engines. In: Proc. of the IEEE 32nd Real-Time Systems Symp. (RTSS). IEEE, 2011. 57-66 . |
| [7] | Kato S, Lakshmanan K, Rajkumar R, Ishikawa Y. Timegraph: GPU scheduling for real-time multi-tasking environments. In: Proc. of the 2011 USENIX Annual Technical Conf. (USENIX ATC11). USENIX Association Berkeley, 2011. 17-31. |
| [8] | Kato S, Throw M, Maltzahn C, Brandt S. Gdev: First-class gpu resource management in the operating system. In: Proc. of the 2012 USENIX Conf. on Annual Technical Conf. (USENIX ATC 2012). USENIX Association Berkeley, 2012. 37-49. |
| [9] | Liu W, Chen JJ, Kuo TW, Deng QX, Liu X. Optimize overall system performance through workload seqencing for gpus data offloading. In: Proc. of the 5th USENIX Workshop on Hot Topics in Parallelism (HotPar 2013). San Jose, USENIX Association Berkeley, 2013. http://hgpu.org/?p=9800 |
| [10] | Hong S, Kim H. An analytical model for a GPU architecture with memory-level and thread-level parallelism awareness. ACM SIGARCH Computer Architecture News, 2009,37(3):152-163. |
| [11] | Oğuz C, Ercan MF, Cheng TCE, Fung YF. Heuristic algorithms for multiprocessor task scheduling in a two-stage hybrid flow-shop. European Journal of Operational Research, 2003,149(2):390-403 . |
| [12] | Schuurman P, Woeginger GJ. A polynomial time approximation scheme for the two-stage multiprocessor flow shop problem. Theoretical Computer Science, 2000,237(1):105-122 . |
| [13] | Hoogeveen JA, Lenstra JK, Veltman B. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard. European Journal of Operational Research, 1996,89(1):172-175. |
| [14] | Garey MR, Graham RL. Bounds for multiprocessor scheduling with resource constraints. SIAM Journal on Computing, 1975,4(2): 187-200 . |
| [15] | Ludwig W, Tiwari P. Scheduling malleable and nonmalleable parallel tasks. In: Proc. of the 5th Annual ACM-SIAM Symp. on Discrete Algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 1994. 167-176 . |
| [16] | Jansen K, Porkolab L. Linear-Time approximation schemes for scheduling malleable parallel tasks. In: Proc. of the 10th Annual ACM-SIAM Symp. on Discrete Algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 1999. 490-498. |
| [17] | Amoura AK, Bampis E, Kenyon C, Manoussakis Y. Scheduling independent multiprocessor tasks. Algorithmica, 2002,32(2): 247-261. |
| [18] | Scharbrodt M, Steger A, Weisser H. Approximability of scheduling with fixed jobs. In: Proc. of the 10th Annual ACM-SIAM Symp. on Discrete Algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 1999. 961-962 . |
| [19] | Diedrich F, Jansen K. Improved approximation algorithms for scheduling with fixed jobs. In: Proc. of the 10th Annual ACM-SIAM Symp. on Discrete Algorithms. Philadelphia: Society for Industrial and Applied Mathematics, 2009. 675-684. |
| [20] | Jansen K, Prädel L, Schwarz UM, Svensson O. Faster approximation algorithms for scheduling with fixed jobs. In: Proc. of the Conf. of Computing: The Australasian Theory Symp. (CATS). Darlinghurst: Australian Computer Society, Inc., 2011. 3-9. |
| [21] | Bougeret M, Dutot PF, Jansen K, Robenek C, Trystram D. Scheduling jobs on heterogeneous platforms. In: Proc. of the Computing and Combinatorics. Berlin, Heidelberg: Springer-Verlag, 2011. 271-283. |
| [22] | Jansen K. A (3/2+e) approximation algorithm for scheduling moldable and non-moldable parallel tasks. In: Proc. of the 24th ACM Symp. on Parallelism in Algorithms and Architectures. New York: ACM Press, 2012. 224-235 . |
| [23] | Jansen K. Approximation algorithms for scheduling and packing problems. In: Proc. of the Approximation and Online Algorithms. Berlin, Heidelberg: Springer-Verlag, 2012. 1-8 . |
| [24] | Xie J, Wang X. Complexity and algorithms for two-stage flexible flowshop scheduling with availability constraints. Computers & Mathematics with Applications, 2005,50(10):1629-1638 . |
| [25] | Sahni SK. Algorithms for scheduling independent tasks. Journal of the ACM, 1976,23(1):116-127 . |
| [26] | Hochbaum DS, Shmoys DB. Using dual approximation algorithms for scheduling problems theoretical and practical results. Journal of the ACM, 1987,34(1):144-162 . |
| [27] | Hall LA. Approximability of flow shop scheduling. Mathematical Programming, 1998,82(1-2):175-190 . |
| [28] | Williamson DP, Hall LA, Hoogeveen JA, Hurkens AJ, Lenstra JK, Sevast’janov SV, Shmoys DB. Short shop schedules. Operations Research, 1997,45(2):288-294. |
| [29] | Jansen K, Sviridenko MI. Polynomial time approximation schemes for the multiprocessor open and flow shop scheduling problem. In: Proc. of the STACS 2000. Berlin, Heidelberg: Springer-Verlag, 2000. 455-465 . |
| [30] | Gupta JND. Two-Stage, hybrid flowshop scheduling problem. Journal of the Operational Research Society, 1988,39(4):359-364. |
| [31] | Chen B. Analysis of classes of heuristics for scheduling a two-stage flow shop with parallel machines at one stage. Journal of the Operational Research Society, 1995,46(2):234-244 . |
| [32] | Schuurman P, Woeginger GJ. A polynomial time approximation scheme for the two-stage multiprocessor flow shop problem. Theoretical Computer Science, 2000,237(1):105-122. |
| [33] | Sevastyanov SV. An improved approximation scheme for the Johnson problem with parallel machines. Journal of Applied and Industrial Mathematics, 2008,2(3):406-420. |
| [34] | Choi BC, Lee K. Two-Stage proportionate flexible flow shop to minimize the makespan. Journal of Combinatorial Optimization, 2013,25(1):123-134 . |
| [35] | Ruiz R, Vázquez-Rodríguez JA. The hybrid flow shop scheduling problem. European Journal of Operational Research, 2010,205(1): 1-18 . |
| [36] | Emmons H, Vairaktarakis G. The Hybrid Flow Shop. In: Flow Shop Scheduling: Int’l Series in Operations Research & Management Science Vol. New York: Springer-Verlag, 2013. 161-187 . |
| [37] | Saravanan M, Sridhar S. An overview of hybrid flow shop scheduling: sustainability perspective. Int’l Journal of Green Computing, 2012,3(2):78-91 . |
| [38] | Oğuz C, Ercan MF, Cheng TCE, Fung YF. Heuristic algorithms for multiprocessor task scheduling in a two-stage hybrid flow-shop. European Journal of Operational Research, 2003,149(2):390-403 . |
| [39] | Moseley B, Dasgupta A, Kumar R, Sarlós T. On scheduling in map-reduce and flow-shops. In: Proc. of the SPAA. New York: ACM, 2011 . |
| [1] | 林一松,杨学军,唐滔,王桂彬,徐新海.一种基于并行度分析模型的GPU功耗优化技术.计算机学报,2011,34(4):706-716 . |
| [2] | 林宇晗,孔繁鑫,徐惠婷,金曦,邓庆绪.线性加速比并行实时任务的节能研究.计算机学报,2013,26(2):384-392 . |
| [3] | 谭国真,孙景昊,王宝财,姚卫红.时变网络中国邮路问题的时间自动机模型.软件学报,2011,22(6):1267-1280. http://www.jos.org.cn/1000-9825/4033.htm |